During the past few decades, due to the diffraction limit of light [1], design, implementation, and application of subwavelength photonic devices, such as waveguides, couplers etc. have faced basic problems and difficulties. In recent years, researchers in the field of plasmonics, investigating the properties and applications of the surface plasmon polaritons (SPP) and localized plasmons [2-4], have introduced a new class of highly miniaturized optical devices to the world [5, 6]. These days SPPs have an important role in the fabri-cation of devices, with a greater confinement of light at nano-scales without limitations due to lightwave diffraction [7].
Surface plasmon polaritons are the coupling of the electro-magnetic fields to coherent charge oscillations of conduction electrons [8, 9], at the interface of the metallic and dielectric materials, that are excited in visible and near infrared wave-lengths. Exciting the SPPs, part of the light energy is trans-ferred to the surface plasmons, so that the reflected wave has lower energy compared to the incident light.
From the application point of view, some novel photonic devices based on SPPs, such as waveguides, directional couplers, reflectors, absorption switches and generalized sensors have been proposed in recent years[ 10-16].
Two specific kinds of multilayer plasmonic structures are insulator-metal-insulator (IMI) and metal-insulator-metal (MIM) [8], but the MIM heterostructures are appropriate geometries in order to obtain better light confinement. The propagation loss of the MIM structures is higher than that of the IMI ones, but in the nanoscale devices it is negligible [17, 18].
Among the band-gap structures, some kinds of plasmonic Bragg reflectors have recently been introduced. A low-loss index-modulated (In-M) Bragg reflector was investigated by Hosseini
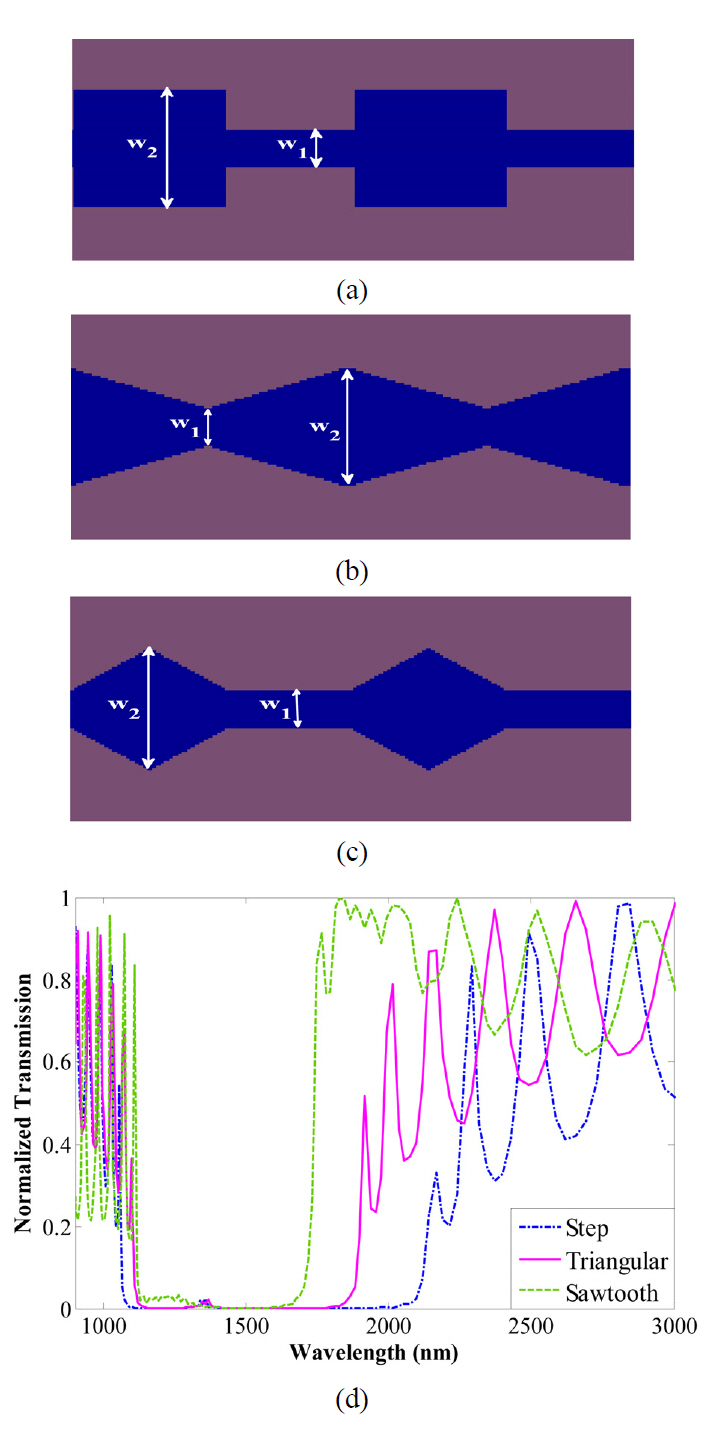
In this paper, we have introduced two new thickness-modulated (Th-M) and index-thickness-modulated (In-Th-M) triangular-shaped grating MIM Bragg reflectors, whose band-gaps are narrower than those of the same Th-M and In-Th-M step-type structures respectively, and wider than those of the similar sawtooth profile structures. In comparison between the sawtooth and triangular-shaped structures, it is revealed that a smoother transmission spectrum could be achieved by the sawtooth profile. Thus, in order to com-pensate the smaller reduction of rippling, the apodization operation is performed on the new triangular Bragg gratings and a smoother transmission spectrum could be achieved compared to the conventional Bragg reflectors.
The dispersion relation of a simple MIM waveguide with the assumption of infinite structure and the form of exp[
where
In this paper, the propagation of SPPs in these structures is simulated, using a two-dimensional FDTD method, accomplished with an auxiliary differential equation (ADE) approach[23]. All the software has been prepared in C++ and Matlab language and environment. The absorbing boundary conditions for all the boundaries of the computational window are convolutional perfectly matched layer (CPML) with the absorption
loss of about -90 dB [24]. The grid sizes in
where
In our simulations, the metallic cladding layers are assumed to be silver, characterized by the Drude dispersion model[25]:
where the material-dependant constants
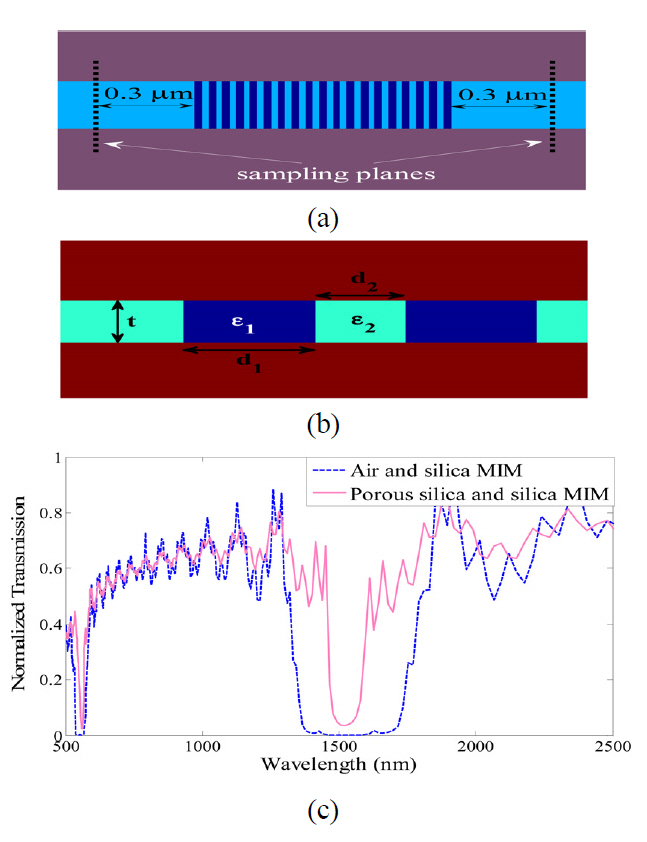
The input and output sampling planes are displayed in FIG. 2.(a), and the number of periods for all the structures is N=19. The normalized transmission can be defined as │
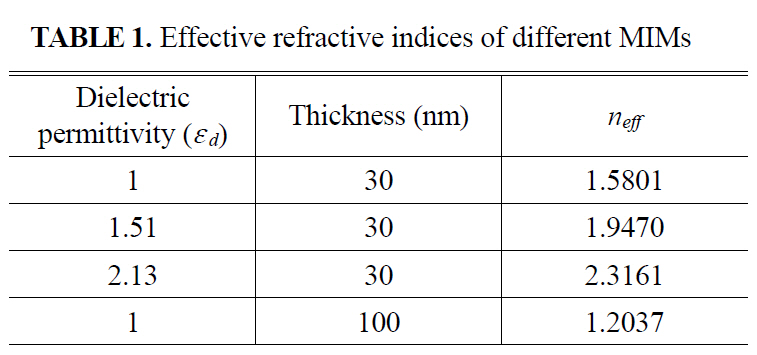
[TABLE 1.] Effective refractive indices of different MIMs
Effective refractive indices of different MIMs
input planes, respectively.
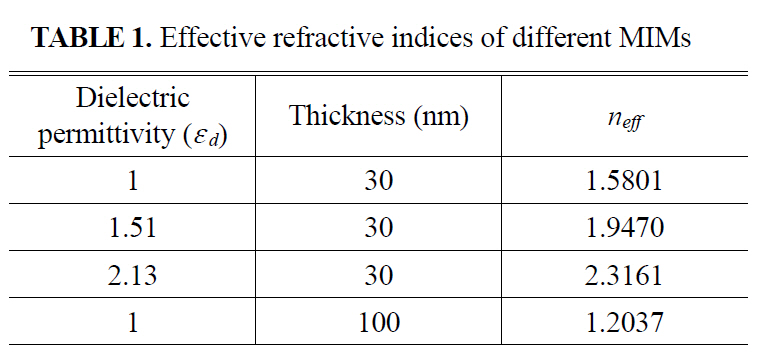
Solving the dispersion relation equations (1-2) in mathematical software, we obtain the effective refractive indices of MIM structures with various dielectrics and insulator widths as given in TABLE 1.
According to the Bragg condition d1
Two different In-M MIM Bragg gratings, with different insulators, illustrated in FIG. 2 have been simulated. In the first one air and silica with
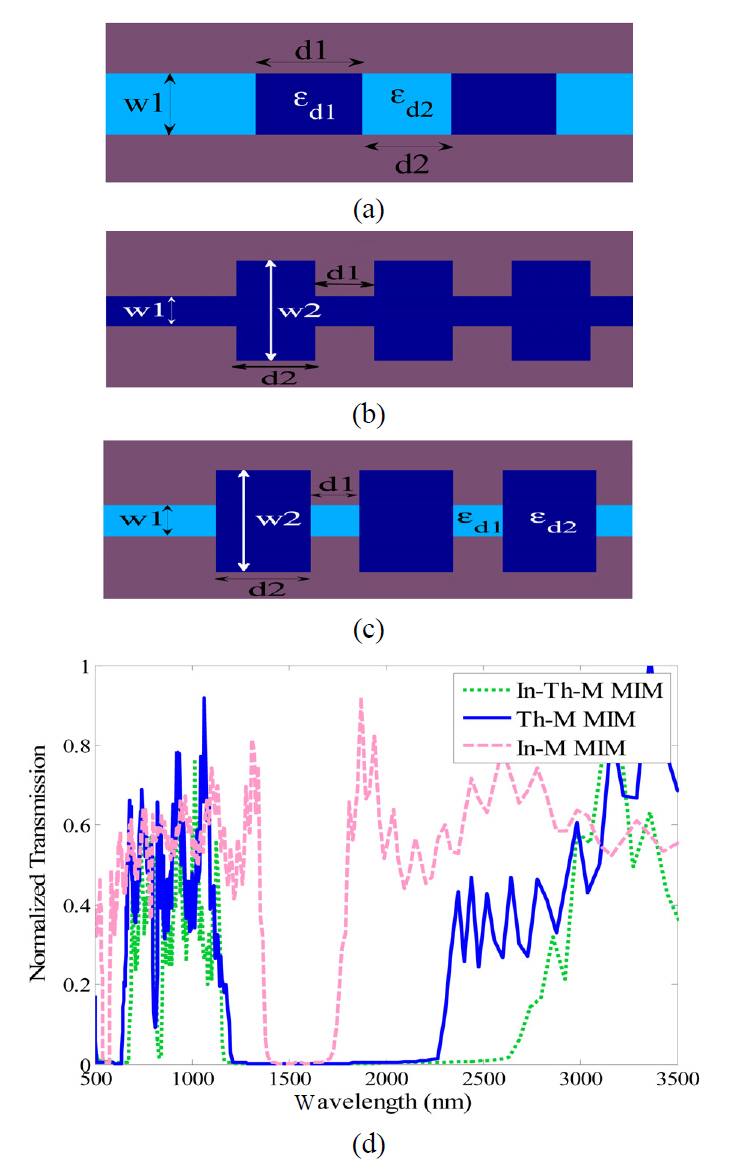
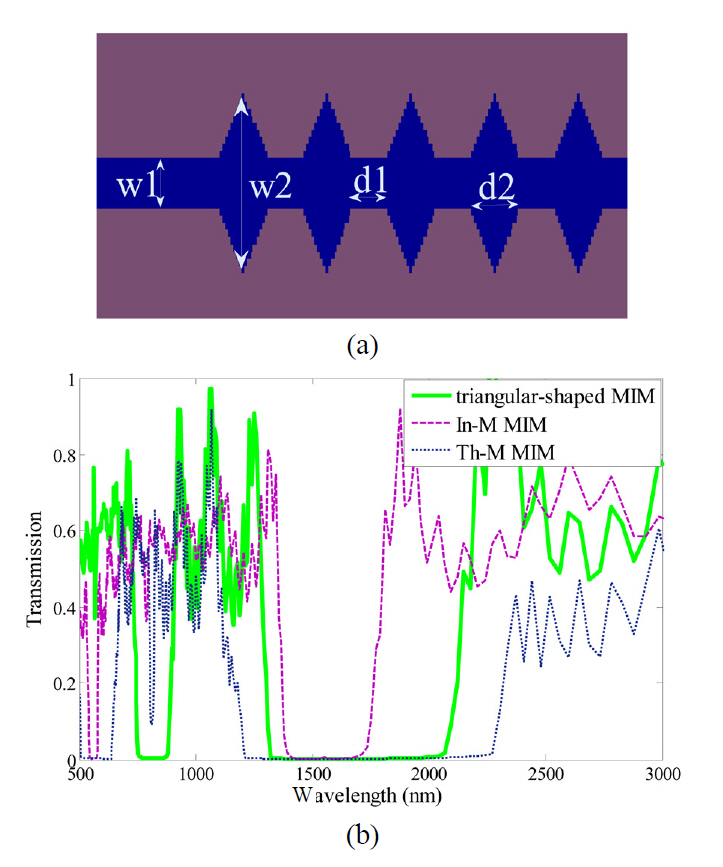
FIG. 3 represents the In-M, Th-M, and In-Th-M MIM structures, which have been analyzed in [13, 14] and [19],respectively by a transfer matrix method. For the Bragg reflector shown in FIG. 3. (a), the dielectric width is w1=30 nm,
Considering the approximated formula for calculating the band-gap width of a 1D photonic crystal [26], and also the equations (1) and (2), for a structure that consists of two alternately stacked MIM waveguides, the parameters that affect the
As demonstrated in FIG. 3. (d), the band-gap of a Th-M Bragg reflector compared to that of the In-M one, and also
the band-gap of an In-Th-M structure compared to that of the Th-M one are wider. In the In-Th-M structure because of utilizing different dielectrics and thicknesses in these MIM waveguides, the contrast between two effective refractive indices of MIM waveguides increases and a wider band-gap is expected.
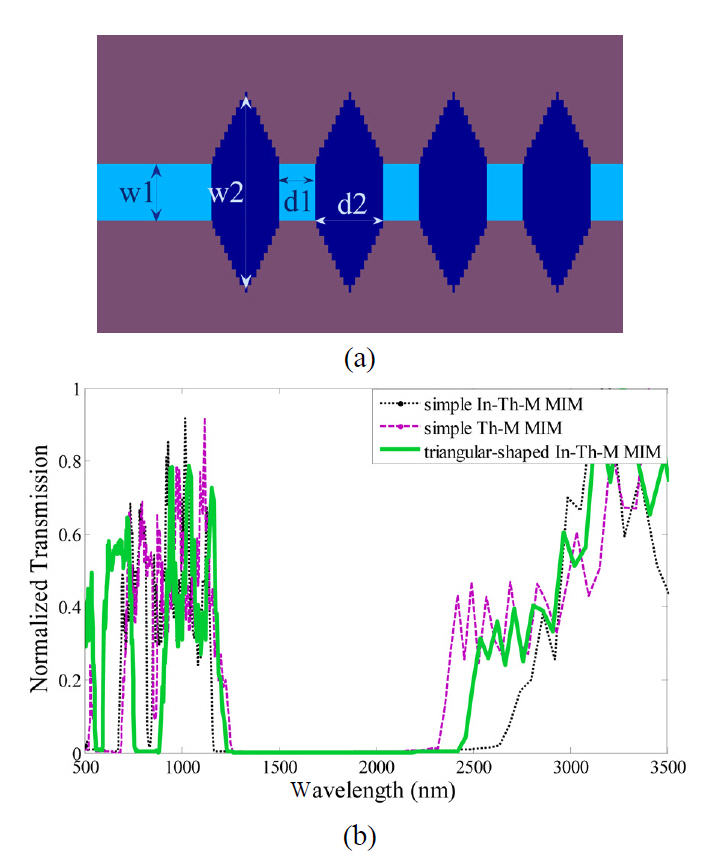
A new triangular-shaped Bragg grating structure shown in FIG. 4. (a), is proposed here. This proposed structure,compared to a simple Th-M MIM with the same w1, w2,d1, and d2, has a narrower band-gap. If we define an effective insulator width as
So, the contrast between the effective refractive indices of the triangular-shaped grating waveguide parts is less than that of a simple Th-M structure, and a narrower photonic band-gap is expected from the triangular-shaped one, as shown in FIG. 4. (b).
With the same reasoning, the band-gap of a triangularshaped grating In-Th-M MIM will be narrower than that of the In-M MIM and wider than that of the Th-M MIM,as illustrated in FIG. 5. (b).
Liu
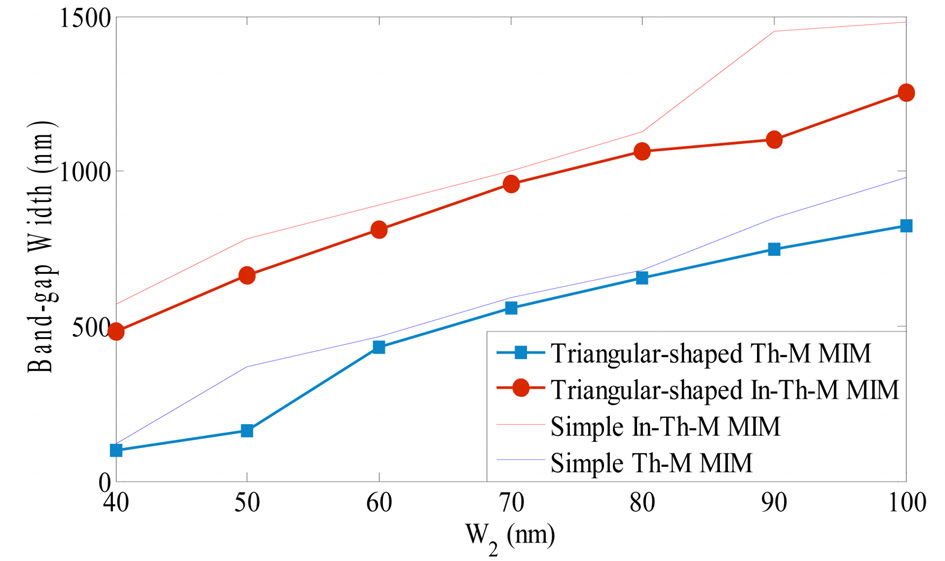
With smaller w2 the band-gaps become narrower. The variation of the band-gap width versus w2 is depicted in
FIG. 7, in which the band-gap is defined as the band where the transmission coefficient becomes under -30dB [20]. In FIG. 7, as w2 increases, the band-gap becomes wider, but as illustrated in FIG. 7 for all values of parameter w2, in both of the triangular-shaped structures the band-gaps are narrower than the similar simple gratings.
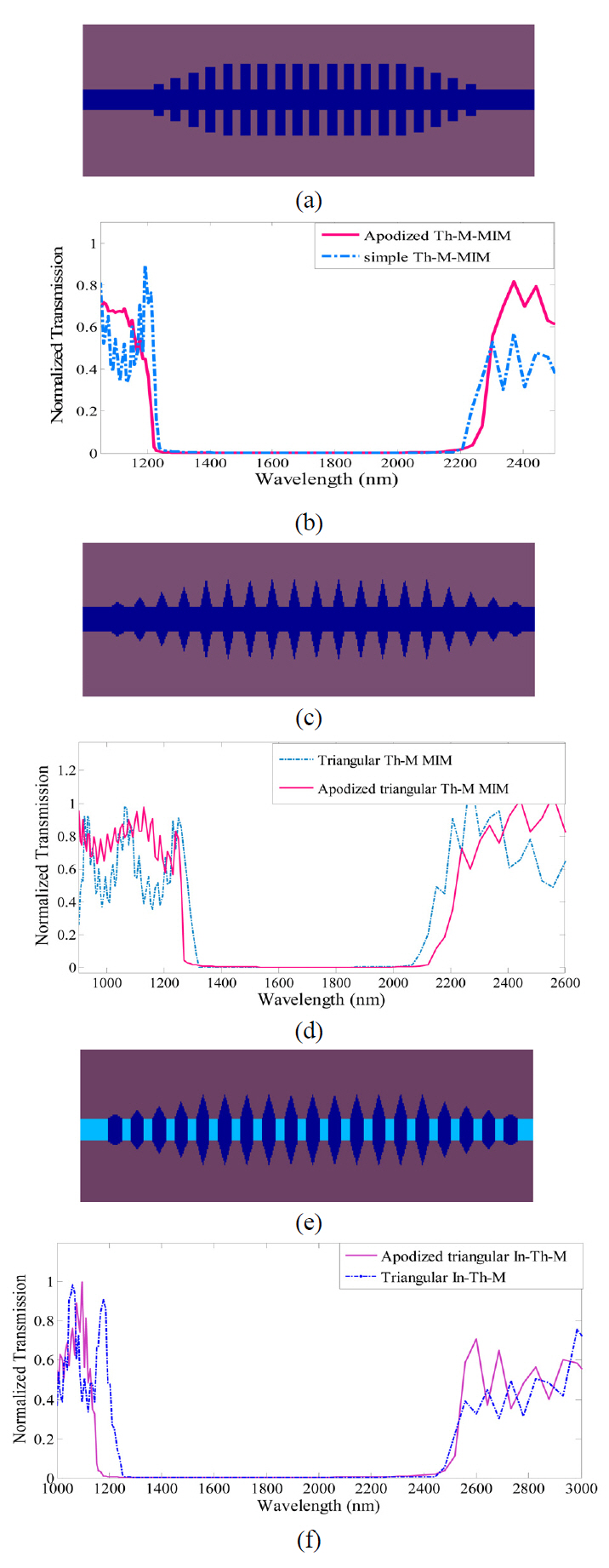
In addition, the depths of the ripples in the triangular and sawtooth shaped reflectors are respectively (18%) and (50%)less than that of the conventional step one. In order to compensate this smaller reduction of the ripples in our proposed structure compared to the sawtooth-shaped reflector, we have utilized the apodization operation.
Shibayama
Now we show that if a similar procedure is performed on the triangular-shaped grating MIMs, the resultant band-gaps would approximately remain as wide as those of the simple gratings, but the side lobes would be noticeably reduced.FIG. 8 illustrates the apodized triangular-shaped grating,Th-M and In-Th-M gratings and also their transmission
In this paper, we have proposed a new triangular-shaped MIM Bragg grating structure, whose band-gap is narrower than that of the simple step and wider than that of the sawtooth-shaped Bragg grating. Also, an apodization procedure has been carried out on these new MIM waveguides, in order to cause the side lobes of the transmission coefficient to be considerably suppressed compared to the conventional simple step Bragg reflectors.