Surface aeration is an important operation in chemical and other processing industries. Surface aeration is defined as the aeration or oxygen transfer that takes place at the gas-liquid surface when the liquid is agitated. The objective of studying aeration process was to interpret the laboratory result for the development of a field installation. This requires a geometrical similarity condition; that is to say the field installation should be built on a definite geometric ratio to that of the laboratory setup. Under a geometric similarity condition, an effective scaleup mandates an awareness of the relative importance of various process parameters at different levels of scrutiny.

Inside a surface aeration tank, different scales of mixing are present, with regions where one of the scales of mixing will prevail, i.e., either macromixing or micromixing. Macromixing is mixing driven by the largest scales of motion in the fluid. Micromixing prevails near the impeller; where small eddies define the velocity gradients surrounding the bubbles. According to Kolmogorov’s theory, the power per unit volume determines the energy and size of the turbulent eddies, which has traditionally been used in the design and scale up of equipment [1-4].

Macromixing prevails adjacent to the micromixing region,which determines the internal homogenization, movement of bubbles across the reactor and flow pattern when the turbulent eddies are tank-sized. The contribution of the surface aeration of a tank, as well as the effect of the geometry of the impeller and the tank to the mass transfer the depend on this scale of mixing [1, 4-8].

Unlike macromixing, which is associated with large-scale fluid motions that can be monitored directly through physical property measurements, micromixing deals with diffusive mixing at the molecular level, for which only indirect methods are available. Despite the availability of much literature on the mixing length scale, mixing scale behavior of surface aerators is typically missing. Recently, Rao and Kumar [9] studied the micromixing behaviors of unbaffled surface aerators. However, baffled type surface aeration systems are mostly preferred in the mixing and chemical industry. Baffles are flat vertical strips set radially along the tank wall, which avoid vortex formation. A baffled tank provides a better concentration distribution throughout the tank and; therefore, improved mixing efficiency is achieved.

Thus, this study aimed to understand the prevalent mixing scale in baffled circular surface aeration systems and obtain scale-up or simulation equations for different mixing scales.

The rate of oxygen transfer depends on the mixing of the liquid in a tank [10-13] and; consequently, both scales of mixing must be considered. The contribution of each scale depends on the internal geometric configuration of the tank.

For a process conducted in a stirred tank, the largest scale of mixing is the scale of the whole reactor. Macromixing refers to flow processes that control the mean concentration and the residence time distribution, i.e., the mean convective flow in the vessel. Macromixing can be characterized by the circulation time, T_m, which can be estimated as [14]:

where Q_C = C₁ND³, and V is the liquid volume in the tank, N the stirring rate, D the impeller diameter, Q_C the circulation capacity,and C₁ a constant.

Small scale mixing in liquids is driven by the mechanism of viscous-convective deformation of fluid elements, followed by molecular diffusion. An important feature of micromixing is the accelerating effect of viscous-convective deformation on molecular diffusion. The micromixing time, τ_m is estimated as follows [15]:

where C is a constant, the dissipation rate of turbulent kinetic energy and the kinematic viscosity.

A characteristic feature of turbulent flow is the presence of a wide range of eddy sizes, ranging from the flow domain, i.e., integral scale eddies, to smaller sizes, i.e., Kolmogorov scale eddies[16]. The large eddies are unstable, interact with each other and the boundaries of the flow, break down into multiple smaller eddies and; thus, transfer their energy to them. First, this transfer is efficient and very little kinetic energy is lost [16]. When the eddies become small enough, in the order of Kolmogorov scale in size, the eddy motion is stable, viscosity takes over and the energy is damped out and converted into heat. This process is usually described as a turbulence cascade, where energy continually flows from a larger to smaller eddies and; on the smallest eddy scale, an ultimate sink of energy is caused by viscous dissipation. This conversion of energy can be quantified using the kinetic turbulent energy dissipation rate, ε. Kresta and Wood [17] investigated the turbulence quantities in a stirred vessel,with the emphasis on energy dissipation. It is assumed that the bulk of the energy is contained in the largest eddies, the flow is in local equilibrium and the flux of energy towards smaller scales is constant. Zhou and Kresta [18] used a dimensional argument and found that most of the total energy was dissipated in the vicinity of the impeller discharge. The direct measurement of ε is very difficult, since it needs to precisely capture the smallest turbulent structures [19].

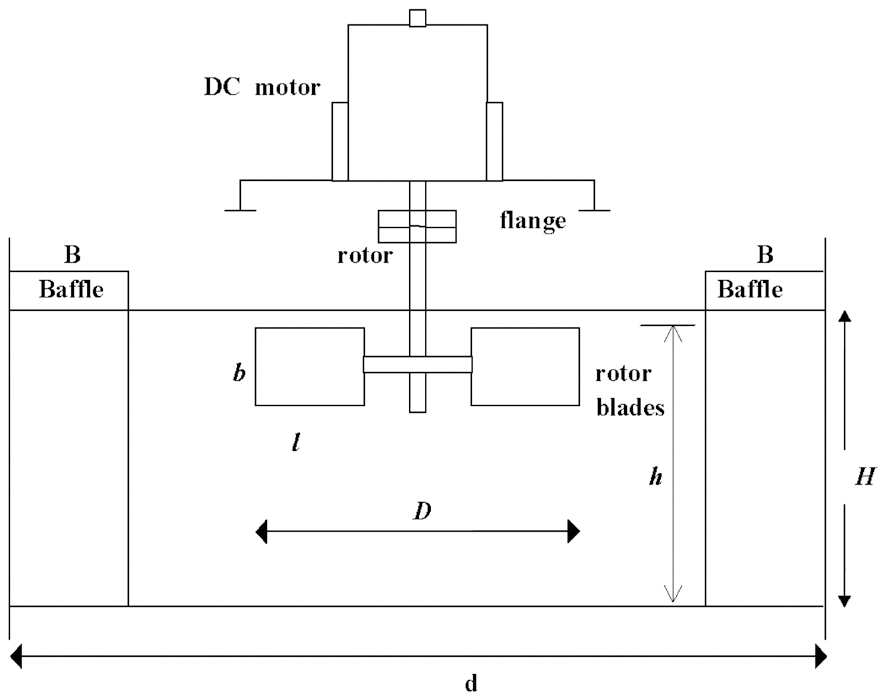
Experimental measurements of the oxygen transfer rate were performed in baffled surface aerators [20], with numerical schemes adopted to calculate the different time scales of mixing.The cross-sectional areas of the tanks tested were A=1 and

0.5184 m². A schematic view of the aerator is shown in Fig. 1.

The following geometric similarity conditions were maintained in the baffled surface aeration systems:

where A is the cross-sectional area of the tank, H the water depth, h the distance between the horizontal bottom of the tank and the top of the blades, D the diameter of the rotor, N_b the number of baffles and B the width of the baffles. It has been found that the oxygen transfer is at a maximum under the above mentioned geometric similarity conditions [20]. Two-film theory[21] has been used to ascertain oxygen transfer rates. According to two-film theory [21], the oxygen transfer coefficient at T℃, K_La_T, may be expressed as follows:

where ln represents the natural logarithm and C_s, C₀ and C_t the dissolved oxygen (DO) concentrations in parts per million(ppm); C_s = the saturated DO concentration, C₀ the initial DO concentration and C_t the DO concentration at time t. The value of K_La_T can be corrected for a temperature other than the standard temperature of 20℃ as K_La₂₀, using the Vant-Hoff Arrhenius equation [22]:

where θ is the temperature coefficient equal to 1.024 for pure water [22]. With known DO concentration (C_t) values measured at regular time intervals (including the known values of C_o at t = 0), a line can be fitted using a linear regression analysis of Equation (4), between the logarithm of (C_s ? C_t) and t. For this purpose, by assuming different but appropriate values of C_s, the regression giving the minimum “standard error of estimate” was taken and; thus, the values of K_La_T and C_s obtained simultaneously. The values K_La₂₀ were computed using Equation (5), with θ = 1.024, as per the standards. Thus, the values of K_La₂₀ were determined for different rotor speeds, N, of the rotors in all the geometrically similar tanks.

Small-scale properties, especially turbulence characteris-

tics, on which the micromixing time depends, play key roles in many mixing applications. The measurement of such small scale properties is difficult and requires specialized equipment not typically available in industrial laboratories and at pilot plants. In the present work, these small scale properties of surface aeration systems were calculated using the commercially available software, Visimix® [23]. The Visimix® [23] program can be helpful in analyzing the mixing parameters in a stirred tank [24-26], and for investigating different scenarios for scale up and changes to the rotor and vessel configurations. For calculation of the macromixing time, Visimix® [23] considers two zones in the tank, depending on the agitator position. The two zones are the parts of the tank volume above and below the agitator, with differing axial flow directions. Macromixing in each of the zones occurs as a result of simultaneous convection and turbulent (eddy) diffusion. The exchange between the zones is; furthermore, assumed to be a result of the radial velocity. Estimation of the micro-mixing time is based on Kolmogorov’s hypothesis of local microscale turbulence. Kolmogorov’s hypothesis of local microscale turbulence is based on a simplified analysis of the transport and dissipation of the kinetic energy of turbulence. For its calculation, Visimix® [23] first calculates the dissipation rates of the kinetic energy, followed by the micromixing time. The calculation procedures are described as follows:

The mean value of the kinetic energy of turbulence, E, at radius, r, of the tank is defined as:

where v is the mean square root velocity of turbulent pulsations corresponding to the largest local linear scale of turbulence.Steady-state transport of the turbulent component of kinetic energy can be described as:

where q is the circulation flow rate through the rotor, v_e the eddy viscosity and h_j the local linear scale of turbulence. The units of the turbulent dissipation rate, ε, are W/kg. Equation (7) can be solved numerically to obtain values of ε at different rotational speeds. It was assumed that the distribution of a solute was controlled by the turbulent diffusivity in the elementary volumes on a linear scale, λ, only; λ is given by:

Inside such elements, as well as smaller elements, the mixing is mainly caused by molecular diffusivity. In a mixing tank, two characteristic values of the scale, λ, exist:

1) Maximum micro-scale, λ_bulk for the bulk of the flow estimated according to Equation (8), with the average turbulent dissipation value in the bulk estimated as:

where λ_bulk is the linear scale of the turbulence in the bulk volume and D_mol the molecular diffusivity of the gas transfer rate.

2) Minimum micro-scale, λ_m for the area with the highest local dissipation, ε_m, with a characteristic micro-mixing time:

The liquid medium in the bulk of the flow is “micromixed” within time t_m1 from entering the mixing tank. Conversely, it is transported with the circulation flow through the agitator zone, with a mean period t_mc = V/q, where V is the volume of water and q the circulation rate. According to probability theory, nearly all the liquid will pass through the ε_m zone within a period of 3 t_mc, and the time of micromixing for the medium cannot exceed:

Thus, there are two independent estimates of the micro-mixing time: t_m1 and t_mc. The lower of the two was selected by the program as the micromixing time; t_m. Calculation of the micromixing time was performed for different rotational speeds.

In this section, experimental and numerical results obtained by Visimix® [23] for the macro and micromixing times were analyzed in order to present simulation equations for them both in geometrically similar surface aeration systems.

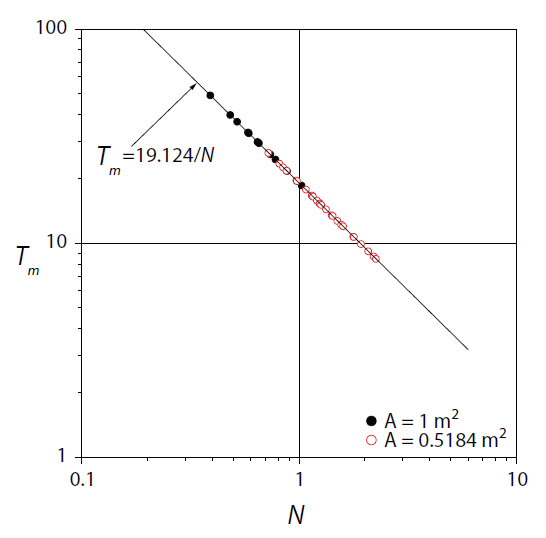
As previously discussed, macromixing is mixing driven by the largest scales of motion in the fluid, and is characterized by the blend time in a batch system. On reanalyzing Equation (1), it was found that T_m was inversely proportional to N, i.e., T_m =C/N. The numerical results obtained using Visimix® for different tanks have been plotted in Fig. 2, where the observations fell on a single line. The equation representing the curve was 19.124/N. The equation representing T_m is also useful in scaling up the macromixing time.

According to the dimensional analysis, the energy dissipation rate is given by [27]:

where α is a constant, v’ a turbulent velocity characteristic and L a characteristic length. The characteristic length, L, can be taken as proportional to the impeller diameter. However, this dimensional analysis assumed that the turbulence was fully developed. Replacing v’ with ND, where N is the rotational speed of the rotor, Equation (12) can be represented as follows [28]:

where K is the proportionality constant. Equation (13) shows that for a particular rotor diameter, ε is proportional to the cube of the rotational speed. To ascertain this fact, the numerically calculated values of ε with rotational speed have been plotted in Fig. 3 for both the surface aerators.

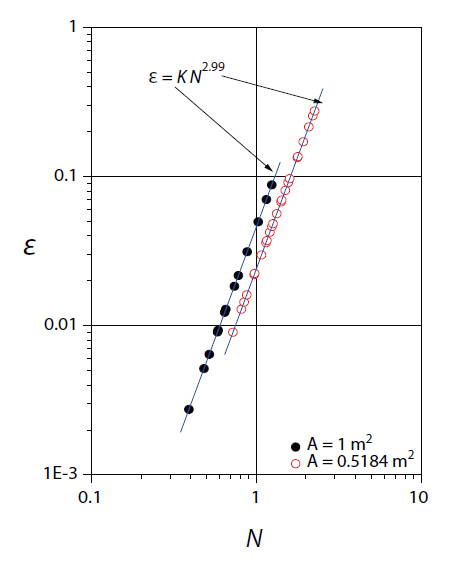
As shown in Fig. 3, regression lines were drawn between the simulated energy dissipation rates and rotational speeds for different sized surface aerators, giving the regression equations:

The correlation for the data using Equation (14) gave a regression coefficient of 0.99. The exponent on the N-term in Equation (14) was very close to the theoretically derived value of 3.

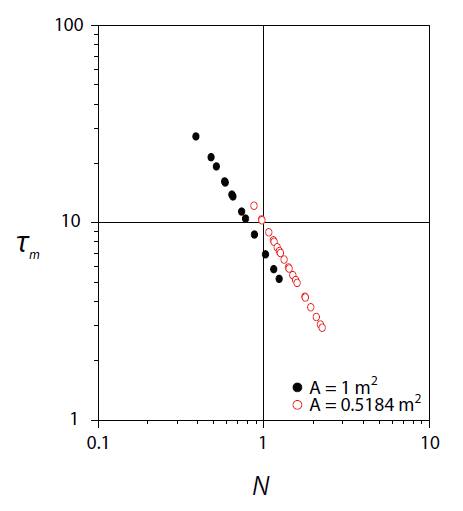
Micromixing is the rate limiting step in the progress of fast reactions,because micromixing dramatically accelerates the rate of production of the interfacial area available for diffusion. The micromixing time can provide useful information on the performance of surface aeration tanks, and takes into consideration the small eddies responsible for the surrounding concentration gradients. The numerical data obtained for the micromixing time were plotted, as shown in the Fig. 4, with respect to the rotor speed, as in the case of macromixing time.

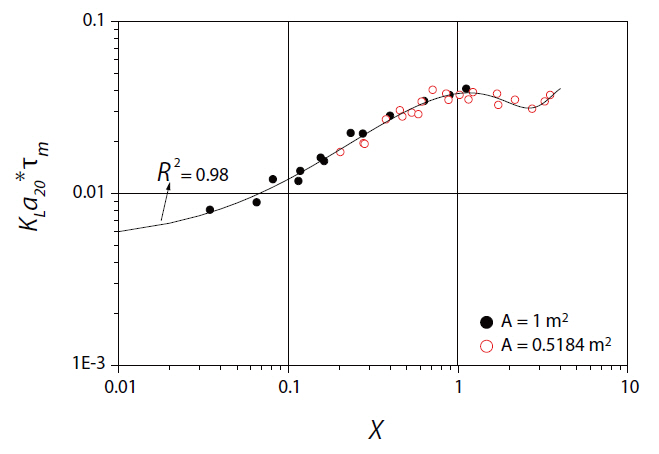
As indicated in Fig. 4, scale effects predominated in the micromixing scale up with rotor speed. The theoretical power per unit volume parameter, X, is a very powerful parameter dealing with agitation, which can be used in scaling up stirred tanks [29,30]. X has been defined as X = N³D²/(g^4/3v^1/3). In order to scale up/simulate the micromixing time, X has been used here as a governing parameter. X is a dimensionless parameter, so in order to make the micromixing time dimensionless; the micromixing time was multiplied by experimental values of the mass transfer coefficients. This multiplied parameter was plotted against X, as shown in Fig. 5; it was found that the data fell on a single curve. This unique representation can be useful in scaling up the micromixing time. The equation representing the curve can be expressed as:

The above equation was valid between the experimental ranges covered in the present paper, i.e., 0.01

Every mixing scale will have a particular effect on the rate of oxygen transfer. Macromixing was found to account for the geometrical configuration of the surface aerator. Micromixing occurred due to turbulent diffusion between small cells in the fluid, which caused the intermingling of molecules. In the present work, simulation equations for the macro and micromixing times in the surface aeration systems have been presented. A simulation equation has been developed that correlates the micromixing time and rate of oxygen transfer in geometrically similar baffled surface aerations for scaling up the process characteristics of surface aeration systems.