With the growing demands for energy in developing countries,sustainable energy production has become more important. Sustainable energy production can be achieved by developing renewable energy conversion technologies and increasing energy conversion efficiencies. It is also important to minimize the environmental impacts of air pollutants emitted from ener-

gy conversion processes. Integrated gasification combined cycle (IGCC) is an important green energy conversion technology, as indicated in the 2009 Korean Energy Roadmap, because the gasification system can process a wide variety of carbonaceous sources, such as coal, biomass, petroleum coke, refinery residue and waste, and also enhance their energy conversion efficiencies [1]. As shown in the schematic diagram of the IGCC system in Fig. 1, the gasification process first converts carbonaceous

sources to a combustible gas. After cleaning and conditioning,the combustible gas is burned in the combustion turbine to drive an electric generator and produce heat, which can be used to generate stream in a steam turbine. This combined mode of combustion and steam turbines significantly increases the energy conversion efficiency [2].

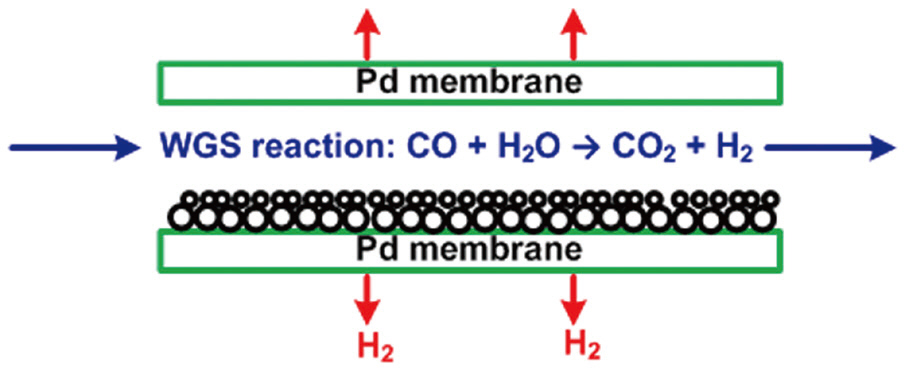
In the gasifier, carbonaceous sources are converted to a mixture of predominantly hydrogen (H₂), carbon monoxide (CO), and carbon dioxide (CO₂). The gasification process can improve the control efficiency of air pollutants, using different techniques, compared to those of conventional post-combustion control devices. Hydrogen sulfide (H₂S) and carbonyl sulfide(COS) are hydrolyzed and removed by an organic solvent. Fuel nitrogen is mainly converted to diatomic nitrogen, with acid gases removed by water scrubbing or amine processes. The carbon monoxide in the cleaned gas stream is converted to CO₂ and H₂ by the reaction with water vapor (H₂O), with the H₂ then separated from this stream. Because of the technical availability and relatively abundant reserves of carbonaceous sources, the gasification process may play an important role in the future supply of hydrogen energy [3, 4]. Recently, hydrogen-selective membranes have been studied for the separation of hydrogen from the gas stream after a water-gas shift reaction, as shown in Fig. 2. In particular, a palladium-based membrane has been reported to have exceptional hydrogen-separating capability; therefore, many publications have reported experimental tests on the performance of the palladium membrane for hydrogen separation [5-8], as well as theoretical investigations based on firstprinciple density functional theory [9, 10]. However, because most of the theoretical studies have focused on the analysis of the electronic structure of the atoms at the palladium surface, additional guidance is necessary for environmental engineers to apply the theoretical study results to the hydrogen separation process using a palladium-based membrane. Especially, in Korea, although a number of experimental studies have been conducted for improving the performance of the palladium-based membrane [11, 12], theoretical research based on first-principle density function theory is an unfamiliar area. Therefore, theoretical calculations were carried out in this study to investigate the dissociative adsorption of hydrogen onto the palladium surface as a function of the adsorption configuration, partial pressure and temperature. This study also described how the theoretical results can be applied to predict the interaction between hydrogen and palladium in the hydrogen separation process using a palladium-based membrane. In addition, further theoretical and experimental investigations have been suggested for improving the hydrogen permeability and cost effectiveness of the palladium-based membrane.

The dissociative adsorption of hydrogen onto palladium was investigated using first-principle density functional theory calculations performed via the Vienna ab initio simulation package. The first-principle methods can describe the surface properties of palladium without applying empirical parameters. The density functional theory is based on the Hohenberg-Kohn theorem,which states “all properties of any system of interacting particles in an external potential is determined by the ground state particle density” [13, 14]. Kohn and Sham formulated the density functional theory via the following equation:

where E is the ground state energy of the system, T[n] the kinetic energy of non-interacting electrons, V_ext(r) the external potential due to the nuclei and any other external fields, E_H[n] the Hartree functional, E_II the interaction between the nuclei and E_XC[n] the exchange-correlation functional. In other words, the density functional theory provides the total energy of the system as a function of the atomic configuration. The reliability of the density functional theory depends on the accuracy of the approximations in the exchange-correlation function. The exchangecorrelation function E_XC[n] can be written as:

where ε_xc[n](r) is the exchange-correlation energy per electron at point r.

One of the approximations in the exchange-correlation energy is called the local density approximation (LDA). The true exchange-correlation energy, ε_xc[n], is approximated using the local exchange-correlation energy, ε_xc ^LDA(n(r)), of the homogeneous election gas:

18

However, since the LDA is known to overestimate the binding energy, the density gradient in the exchange-correlation energy is included so that the non-homogeneity of the true electron density can be considered and the approximation developed:

20

This approach is called the generalized gradient approximation (GGA).

As shown in Fig. 3, this study considered a clean Pd(111) p(2×2) surface structure, consisting of an ideal periodic structure of 4 layer slabs, with several adsorption sites, such as top,face-centered cubic (fcc) and hexagonal closed packed (hcp) sites. The density functional theory provides energetic information at zero temperature and zero pressure. Further information for the realistic temperatures and pressures can be obtained using standard thermodynamics methodology [15-17]. For an ideal crystal, the surface free energy is defined by the following equation:

where γ is the surface free energy per unit area, A the surface area, ΔG_surface the Gibbs free energy introduced through the surface,G the Gibbs free energy of the total system, G_solid the Gibbs free energy from the solid bulk, and G_gas the Gibbs free energy from the homogeneous gas. Since a lower Gibbs free energy indicates a more stable state system, the most stable surface structure has the lowest surface free energy. The Gibbs free energy of adsorption (ΔG_ad) is determined from the difference in the surface free energy between the clean surface (γ_clean) and hydrogenadsorbed surface (γ_ads), which can be used to evaluate the stability of hydrogen on the palladium surface at a given temperature and pressure:

where N_H and N_Pd are the numbers of atoms of hydrogen and palladium, respectively, and μ_H the chemical potential of hydrogen.Since a more stable structure has lower surface free energy, the most stable structure of a hydrogen-adsorbed surface has the most negative Gibbs free energy of adsorption at the corresponding chemical potential of hydrogen. In addition, the Gibbs free energy is defined by several energy terms, as follows:

where E^total is the total energy, F^vib the vibrational free energy, and F^conf the configurational free energy. Because this study evaluated the difference in the Gibbs free energies at less than 100 atm, the F^conf and pV were assumed to be negligible. The chemical potential of hydrogen in Equation (6) can also be determined by the following energy terms:

where E^total_H2 and E^ZPE_H2 are the total and zero point energies, respectively. The following adsorption energy term is also defined:

where E_Pd+H2, E_Pd and E_H2 represent the energies of the hydrogenadsorbed palladium surface, the palladium bulk and the adsorbate hydrogen, respectively, and N_H the number of hydrogen atoms. Then, the final Equation (10) is obtained for evaluating the stability of the hydrogen adsorbed onto the palladium surface as functions of the temperature and pressure.

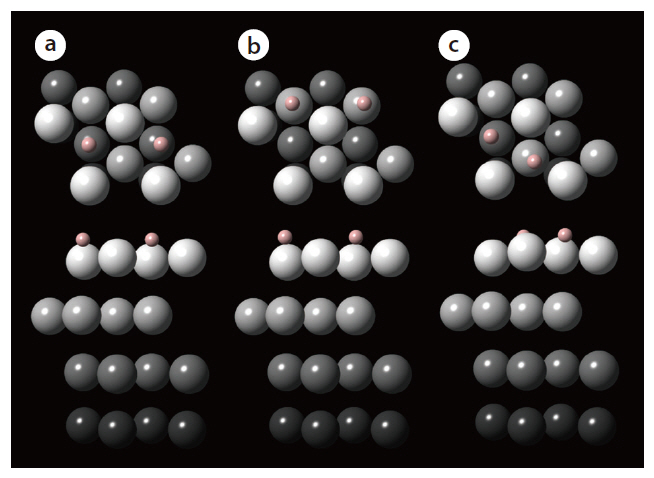
The adsorption energies of hydrogen (H₂) onto the hollow adsorption sites of the palladium surface are determined from calculations performed using the Vienna ab initio simulation package. The exchange-correlation energy is described by the generalized gradient approximation (GGA). From preliminary geometry relaxation and frequency of gas-phase hydrogen calculations, the cutoff energy for the plane-wave basis sets and Methfessel-Paxton smearing were determined to be 350 eV and 0.1 eV, respectively. In addition, a 7 × 7 × 1 k-points mesh size was found to be optimal. The adsorption of hydrogen was investigated for the representative favorable adsorption sites of the simulated palladium surface: 1) fcc-fcc, 2) hcp-hcp, and 3) fcc-hcp. Fig. 4 describes the final configuration of the hydrogen adsorbed onto each adsorption site of the palladium surface. The adsorption energy of a dissociated hydrogen atom was also determined for each adsorption structure, with that onto the fcc-fcc

site showing the most negative energy, indicating the strongest binding of hydrogen. In addition, energies more negative than-0.43 eV for all adsorption sites indicates that the adsorption of hydrogen onto palladium may be classified as chemisorption. As shown from these calculation results, a study based on firstprinciple density functional theory provides information on the stability of the hydrogen binding onto the crystal surface; therefore,the first-principle method can be applied to find materials with a good capability to separate hydrogen.

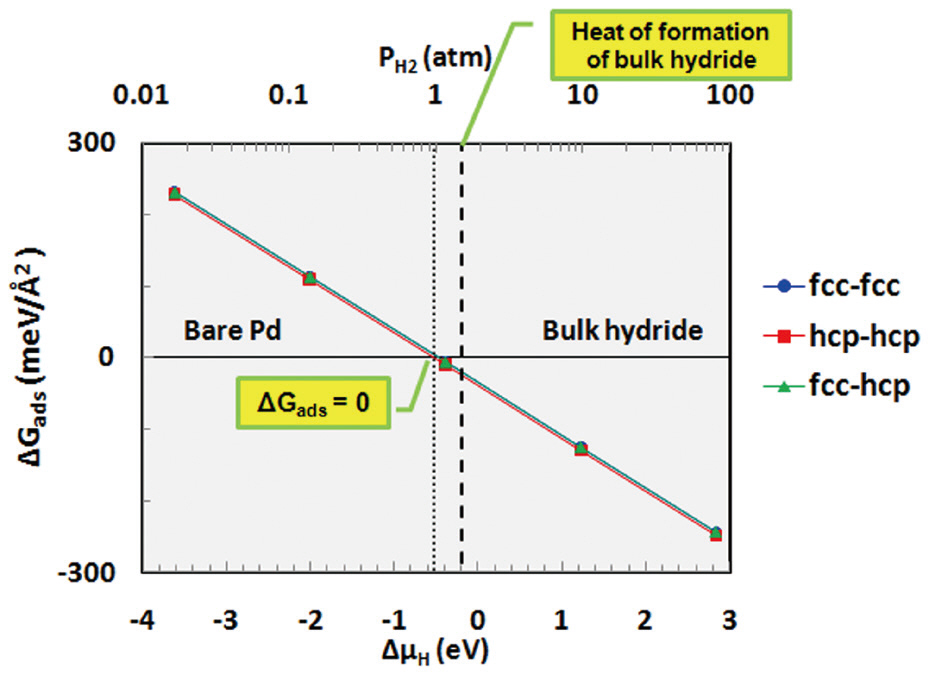
Thermodynamic calculations were performed using Equation (10) to investigate hydrogen binding as function of the pressure and temperature. The Gibbs free energy of adsorption(ΔG_ads) was determined for the adsorption of hydrogen onto each site of palladium as a function of the chemical potential (or partial pressure) of hydrogen at 600 K, as shown in Fig. 5. As mentioned in Equation (6), when bare palladium has a lower surface free energy than the hydrogen-adsorbed surface (when the Gibbs free energy of adsorption is positive), it is considered to have a more stable structure. As shown in Fig. 5, ΔG_ads decreases with increasing hydrogen content in the gas phase. Hydrogen is considered to be stabilized on the palladium surface when ΔG_ads becomes negative; therefore, Fig. 5 indicates that hydrogen may be stabilized on the palladium surface at around more than 1 atm at a temperature of 600 K. Bulk hydride is also formed on the palladium surface when the chemical potential of hydrogen increases to more than the heat of formation of the bulk hydride.In addition to the effect of the partial pressure of hydrogen, ΔG_ads was also obtained as a function of the temperature for the fcc-fcc adsorption site, as shown in Fig. 6. This figure shows that hydrogen may be more stable on the palladium surface with decreasing temperature at a partial pressure of 1 atm. As described, the results of the thermodynamic calculations provide information on the stability of hydrogen as functions of the partial pressure and temperature.

First-principle density functional theory calculations were performed to investigate the stability of hydrogen adsorbed onto the palladium surface as functions of the adsorption configuration, partial pressure and temperature. As a result, hydrogen was indicated to be chemisorbed onto the palladium surface, with hydrogen expected to be stabilized on the surface at partial pressures of hydrogen above 1 atm at equilibrium. Further study is suggested to find the best alloying metal and composition of the palladium alloy for improving the hydrogen permeability and cost effectiveness of the palladium-based membrane. For the addition of a certain alloying metal to the palladium surface,the binding energy of hydrogen onto the palladium alloy can be determined as functions of the partial pressures and temperatures via theoretical calculations. The alloying material determined from the theoretical studies can be experimentally tested to confirm its performance in the production of hydrogen. Experimental tests can be carried out by locating each palladiumbased membrane in a pressure-controlled reactor. The hydrogen permeability of the membrane can be determined based on the difference in the pressures between inlet and outlet of the membrane reactor.