Within the satellite communications innovation trend, key issues related to frequency band, frequency reuse, satellite RF power, and adaptive coding and modulation (ACM) techniques are shifting the focus from classical modulation schemes for satellite communications, such as quadrature phase shift keying (QPSK) and Gaussian minimum shift keying (GMSK), to higher order M-ary modulation schemes with a higher spectral efficiency. The high order modulation schemes are indispensable to providing new multimedia services and to achieving the convergence of communication and broadcasting. The modulation schemes must be less sensitive to AM/ AM and AM/PM distortions due to the nonlinearity of a high-power amplifier (HPA). The HPA, an important element in modern communication systems, provides the transmission signal level to overcome the transmission loss between a transmitter and a receiver. However, the nonlinearity of HPA, that is, the AM/AM and AM/ PM characteristics, distorts the transmitted signal and eventually degrades the error performance. Therefore, the digital video broadcasting-satellite2 (DVB-S2), which was recently established as a standard of digital satellite broadcasting by European Telecommunications Standards Institute (ETSI), has adopted the high-order amplitude phase shift keying (APSK) modulation schemes (4+12 APSK and 4+12+16 APSK) that shows a better performance with respect to the HPA nonlinear characteristics in order to increase the transmission capacity (ETSI 2009). Consultative Committee for Space Data Systems (CCSDS), the protocol used in satellite communications and deep space communications as the international standard, recently reported the experimental results of applying APSK modulation schemes for high-speed telemetry data transmissions (CCSDS 2003, 2007).

Recently, for 4+12 APSK and 4+12+16 APSK, new bitsto- symbol mappings that have robustness against the nonlinear distortion caused by HPA in satellite communications was reported (Kim et al. 2007). Kim et al. (2007) analyzed the effects of the nonlinear distortion on the signal constellation for 4+12 APSK and 4+12+16 APSK and proposed new bits-to-symbol mappings that are less affected by nonlinear distortion. However, though the bits-to-symbol mappings suggested by Kim et al. (2007) have a better performance on bit error rate (BER), those have more complex mapping structures than the bits-to-symbol mappings presented in the DVB-S2 standard.

In this paper, we propose a new bits-to-symbol mapping scheme that has simpler mapping structure and a better BER performance for 4+12+16 APSK in the nonlinear additive white Gaussian noise (AWGN) channel. We also present a simpler bit detection algorithm from the proposed bit mapping scheme. For this purpose, we first analyze the relation among the signal constellation, distances (Hamming distance and Euclidean distance) between the signal points on the constellation, and BER performance depending on the nonlinearity of HPA. Then, bits are assigned to symbol so that the signal points of which Euclidean distance is reduced by nonlinear distortion of the HPA can have a smaller Hamming distance. To validate the proposed bit mapping scheme, the BER performance and the total degradation (TD) depending on input back-off (IBO) are analyzed in comparison with the conventional bit mappings. Moreover, a simpler bit detection algorithm is derived from the approximation of the decision boundary on the proposed bit mapping algorithm and its BER performance is analyzed to verify the derived algorithm.

The rest of the paper is organized as follows: Section 2 describes the system model assumed in this paper. A new bits-to-symbol mapping scheme appropriate to nonlinear AWGN channel is proposed in Section 3. In Section 4, a simpler bit detection algorithm is presented from the proposed bit mapping structure. Section 5 analyzes the performances of the newly proposed bit mapping and detection algorithms. Finally, conclusions are drawn in Section 6.

We assume the system where the information bits through a pulse shaping filter are transmitted via AWGN channel after being modulated to 4+12+16 APSK signal, as shown in Fig. 1. Here, square-root raised cosine (SRRC) filter is used as the pulse shaping filter and the 4+12+16 APSK signal passes through the HPA with nonlinearity before the transmission. The nonlinear characteristics of the HPA distort the input signals in their amplitude and phase. These distortions, respectively called AM/AM and AM/PM, generate unwanted signals in in-band and out-of-band. The unwanted signal generated in in-band distorts the transmitted signals and the unwanted signal generated in out-of-band causes adjacent channel interference so that the error performance is degraded.

The HPA is used for various wireless communication equipments such as transponders of satellite, satellite

earth stations, base stations of mobile communication system, and wireless mobile terminals. In this paper, travelling wave tube amplifier (TWTA) that is usually used in transponders of satellite and satellite earth stations is employed, and Saleh’s model (Saleh 1981) which is widely used for amplitude and phase transfer functions of the TWTA is considered. When the input signal x_i(t) = r_icos(2π∫_ct+ψ_i) passes through the HPA, the corresponding output signal is expressed as

where r_i and ψ_i are the modulated envelope and phase, respectively; A(r_i) and φ(r_i) represent the AM/AM and AM/PM conversions, respectively. The transfer functions (Saleh 1981) of these two conversions are given by

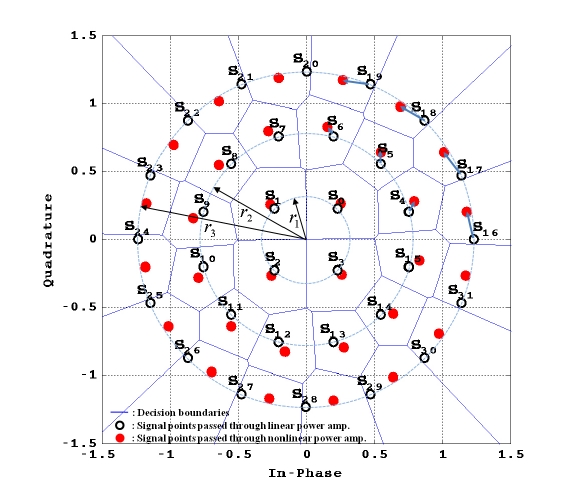
The constellation of 4+12+16 APSK is composed of innerring, middle ring and outer ring, each with uniformly

spaced PSK points. The three rings have the radii r₁, r₂, and r₃, respectively. Fig. 2 shows 4+12+16 APSK constellation and decision boundaries varying with the nonlinearity of the HPA when an IBO is 9 dB. Here, we assume that all the signal points have equal a priori probabilities, and the decision boundaries are determined by the shifted signal points. We also consider the normalized average energy, i.e., [Equation Ommited], i=0,1,...,31, which implies that the radii ,r_j,j=1,2,3 are normalized such that (4r₁² + 12r₂² + 16r₃²)/32=1. As shown in Fig. 2, when the signals are transmitted through the nonlinear HPA, the signal points are shifted due to AM/AM and AM/PM distortions so that, as the nonlinearity increases, the middle ring becomes closer to the outer ring. In particular, the Euclidean distance between the signal point on the middle ring and that on the outer ring, which are located on the diagonal while Hamming distance (H_d(s_i,s_j)) equal to 3, is smaller. It is a dominant cause of the error performance degradation. Thus, if a bits-to-symbol mapping can be achieved so that the Hamming distance between the signal points with the small Euclidean distance becomes smaller, we can expect a better BER performance.

BER is proportional to Hamming distance and inversely proportional to Euclidean distance. Thus, minimizing the Hamming distance between the adjacent signal points in bit mapping is one way to obtain a better BER performance.

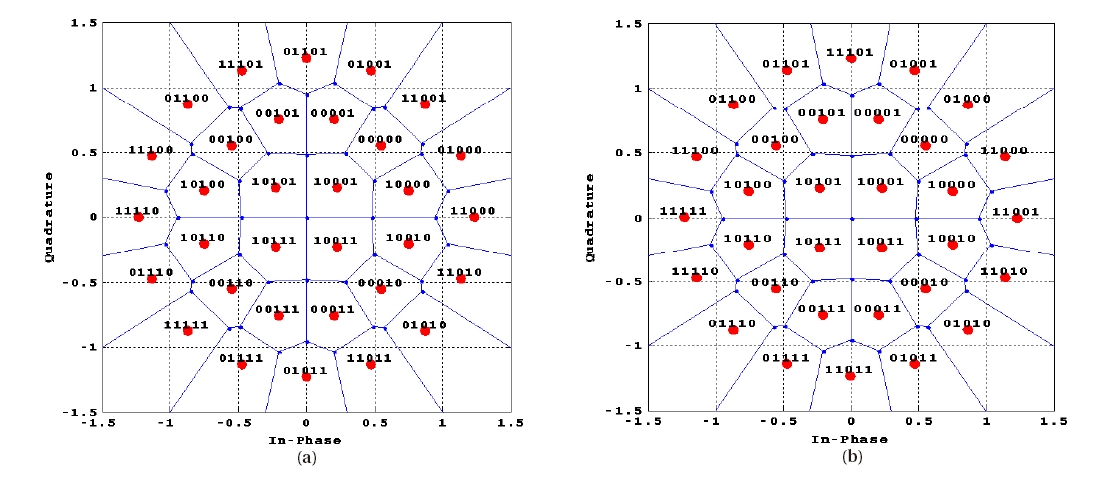
Fig. 3a shows the signal constellation and the bits-to-symbol mapping of 4+12+16 APSK that is presented as the DVB-S2 standard. In the constellation of the 4+12+16 APSK, a Gray mapping where Hamming distance between adjacent symbols is 1 cannot be perfectly applied. In particular, as shown in Fig. 2, the signal points on the middle ring move outwards and the signal points on the outer ring move inwards due to the HPA nonlinearity. Therefore, the bit mapping presented in the DVB-S2 standard degrades the BER performance since the signal points with the largest Hamming distance become close to each other.

If we assume the set of the signal points on the inner ring, S_I = [s₄,s₁₂,s₂₀,s₂₈], the set of the signal points on the middle ring, S_M = [s₂,s₅,s₈,...,s₃₂], and the set of the signal points on the outer ring, S_O = [s₁,s₃,s₆,...,s₃₁], the Hamming distances between the signal points on each ring are expressed as

And, the Hamming distances between the signal points located on the diagonal line of the middle ring and the outer ring in the first and third quadrants are given as

In Fig. 2, carefully observing the two signal point pairs given in Eq. (4), we can see that the Euclidean distances between the two signal points paired decrease due to the HPA nonlinearity. As already mentioned in previous subsection, bits-to-symbol mapping with a large Hamming distance as well as small Euclidean distance degrades the BER performance. Thus, the objective of this section is to develop bits-to-symbol mapping scheme to reduce the Hamming distance between the signal points approaching toward each other due to the HPA nonlinearity so that the BER performance can be improved. For this, the 32 symbols of the 4+12+16 APSK are firstly located on the polar coordinates and listed in order of θ as follows:

If θ_i = θ_j,i≠ j for the i-th and j-th symbols, a priority is given to the symbol whose signal amplitude, r_i, is smaller.

The 32 symbols in order are grouped, with 8 symbols on the same quadrant as much as possible, and divided into 4 symbol sets, R_k,k=1,2,3,4, as given by

And then, bits are mapped to each symbol grouped into 4 sets. For the sake of convenience, order on bit for the description of the bit mapping scheme bases on the similarity of mapping pattern. That is, the third, fourth, second, first and fifth bits are explained in order in this paper.

For the third bit (b_i,3), the bit value 0 is assigned to the symbols included in the R₁ and R₄ sets, while the bit value 1 is assigned to the symbols included in the R₂ and R₃ sets. For the fourth bit (b_i,4) the bit value 0 is assigned to the symbols included in the R₁ and R₂ sets, while bit value 1 is assigned to the symbols included in the R₃ and R₄ sets. Here, ,b_i,h denotes the h-th bit of i-th symbol.

These can be mathematically expressed as

- The third bit (h = 3)

- The fourth bit (h = 4)

The first, second and fifth bits (b_i,1, b_i,2, and b_i,3) are allocated in order of the amplitudes of the elements in the symbol set R₁. For the second bit, let’s assume that A = [a₁a₂...a₈] is the set where the amplitudes of the symbols, r_i = 's_i', i = 1,2,...,8 in R₁ are rearranged in ascending order. If the amplitude of a symbol, r_i, belongs to the set of small amplitudes, {a₁...a₄}, bit value 0 is assigned to the symbol, while bit value 1 is assigned if it belongs to the set of large amplitudes, {a₅...a₈}. This can be mathematically given as

- The second bit (h = 2)

The first bit (b_i,1), and the fifth bit (b_i,5), are allocated to each symbol so that the allocated bit mapping structure can be symmetric. Let’s assume that B = [b₁b₂...b₈] is a set where the quadrature (Q)-axis components, s_{i_Q}, i=1,2,...8, of the symbols included in R₁ are rearranged in ascending order. If the absolute Q-axis component of a symbol, 's_{i_Q}', belongs to the subset with large magnitudes of the set B, {b₅...b₈}, bit value 0 is assigned to the symbol, otherwise bit value 1 is assigned. The fifth bit is allocated in a similar method with the first bit. Let’s assume that C = [c₁c₂...c₈] is the set where the inphase (I)-axis components, si_{_I}, j = 1,2,...,8, of the symbols included in R₁, are rearranged in ascending order. If the absolute I-axis component of a symbol, 's_{i_I}', j = 1,2,...,8, belongs to the subset with large magnitudes except the largest magnitude of the set C, {c₄...c₇}, bit value 0 is assigned to the symbol, otherwise bit value 1 is assigned. These can be mathematically given as

- The first bit (h = 1)

- The fifth bit (h = 5)

Fig. 3b shows the bits-to-symbol mapping of the bits allocated to all the signal points by Eqs. (7-11). As can be seen from Fig. 3b, in the proposed bits-to-symbol mapping for 4+12+16 APSK, the Hamming distances between the adjacent symbols making the decision boundary are only 1 or 2. Especially, the Hamming distances between the two symbol pairs that have the largest Hamming distance in the conventional mapping are just 1 which is the minimum, as

Decrease of Hamming distance can give potentially a better BER when the transmitted signals are distorted by the HPA nonlinear characteristics. Moreover, in contrast to the standard bit mapping where only the second bit is symmetric and the bit mapping suggested by Kim et al. (2007) where only the third bit is I/Q symmetric, the newly proposed bits-to-symbol mapping provides I/Q symmetry for the first, second, and fifth bits. This can reduce the burden to the receiver in detecting signals in comparison with the conventional mappings.

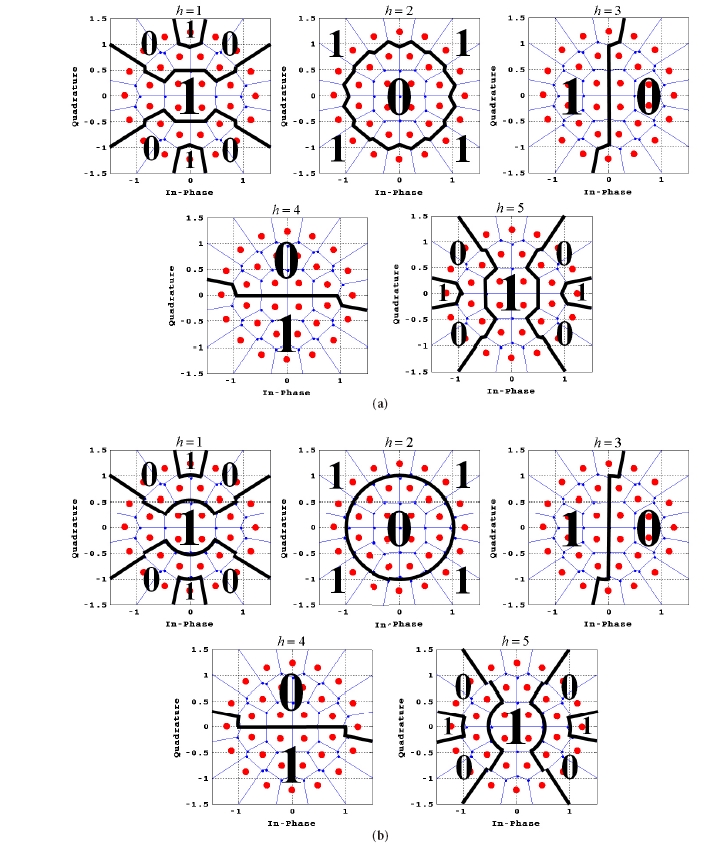
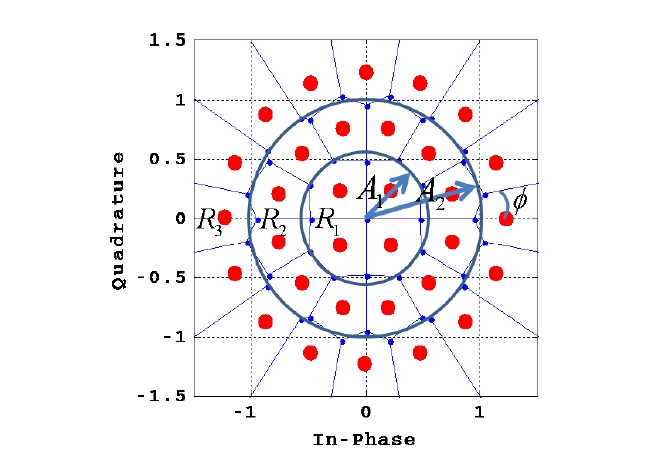
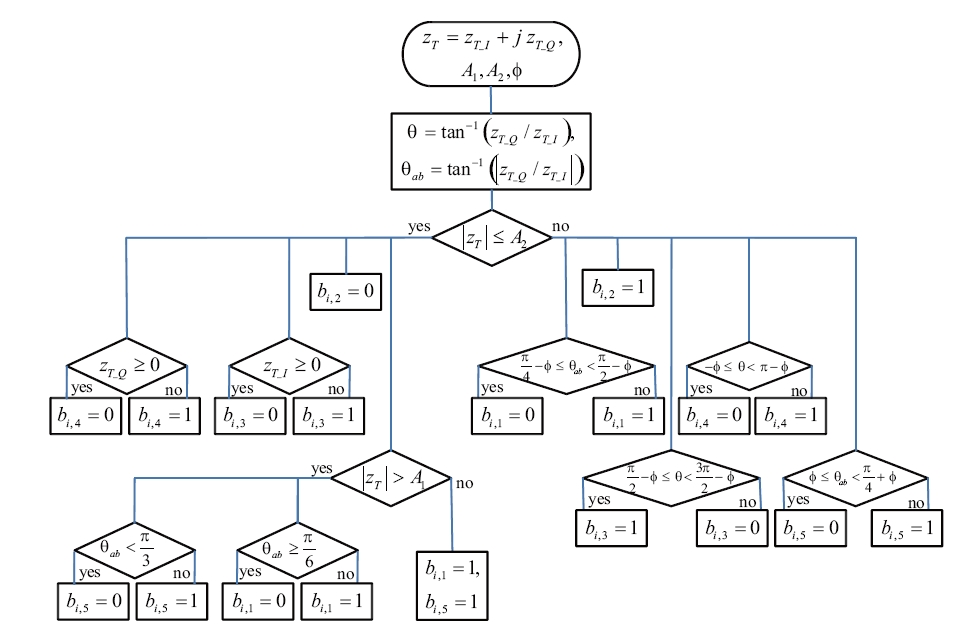
In this section, a simple bit detection algorithm is presented through the decision boundary approximation of each bit for the newly proposed bit mapping. First, the exact decision boundary of each bit (Fig. 4a) that can be known from Fig. 3 is approximated as in Fig. 4b. Then, the bit detection using the approximated decision boundary is carried by dividing a whole region into the three regions, R1, R2, and R3. Fig. 5 shows the region division for bit detection. The three regions can be given using the received signal Z_T as follows:

where A₁ and A₂ are the distances from the origin to the boundaries of the three regions.

The third and fourth bits are detected by firstly determining whether the received signal Z_T belongs to the R₁∪R₂ region (z_T' ≤ A₂) or it belongs to the R₃ region(z_T' > A₂ ), since their bit mapping structures are not symmetric to I and Q axes. The first and fifth bits are

detected by using the absolute values of the I-axis component (z_{T_I}) and the Q-axis component (z_{T_Q}), since the bit mapping structures for the bits are I/Q symmetric. As the preceding condition of the third and fourth bits is the boundary to determine the second bit, those are detected according to the preceding condition. The detection procedure of each bit is given as

- The first bit (h = 1)

- The second bit (h = 2)

- The third bit (h = 3)

- The fourth bit (h = 4)

- The fifth bit (h = 5)

In Eqs. (16) and (17), θ = tan^-1(z_{T_Q}/z_{T_I}) and in Eqs. (14) and (18), θ_ab = tan^-1'(z_{T_Q}/z_{T_I})'. In addition, A₁ = 0.55, A₂ = 1.01, and φ=π/16. Fig. 6 shows the flow chart of the bit detection algorithm.

In this section, the BER performance and TD of the 4+12+16 APSK for the proposed bits-to-symbol mapping are compared with those for the conventional bit mappings by the DVB-S2 standard and Kim et al. (2007) according to the various IBOs in the nonlinear AWGN channel. In addition, the bit error performance of the proposed simple bit detection algorithm using the approximated decision boundary is analyzed.

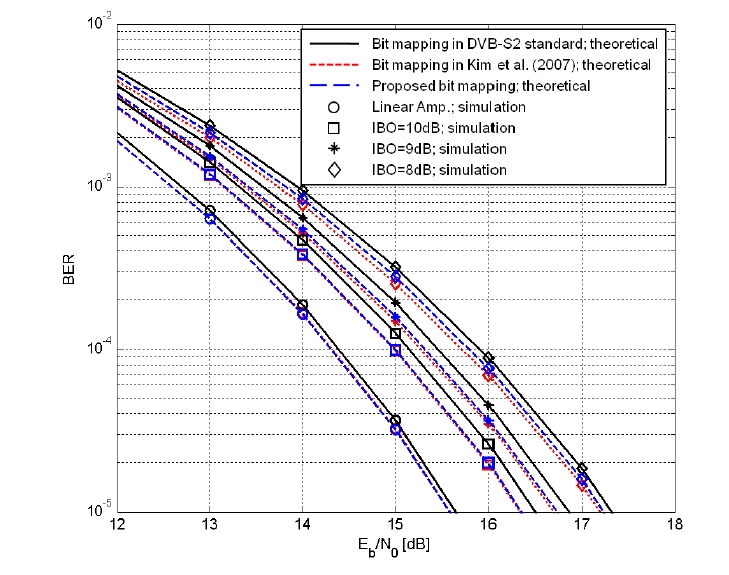
Firstly, for the performance analysis of the proposed bit mapping, we consider IBOs of the 8, 9 and 10 dB and set the ring ratios of the 4+12+16 APSK to γ = R₂ / R₁ = 2.42 and γ = R₃ / R₁ = 3.73. Also, the roll-off factor of the SRRC filter is set to 0.35. The theoretical results are obtained by using the exact BER expressions provided by Lee et al. (2007). TD is obtained by adding the difference between SNR values in the linear and nonlinear AWGN channels for satisfying the target BER to IBO (or output backoff [OBO]). In this paper, the TD calculation is performed at the target BER of 10^-5

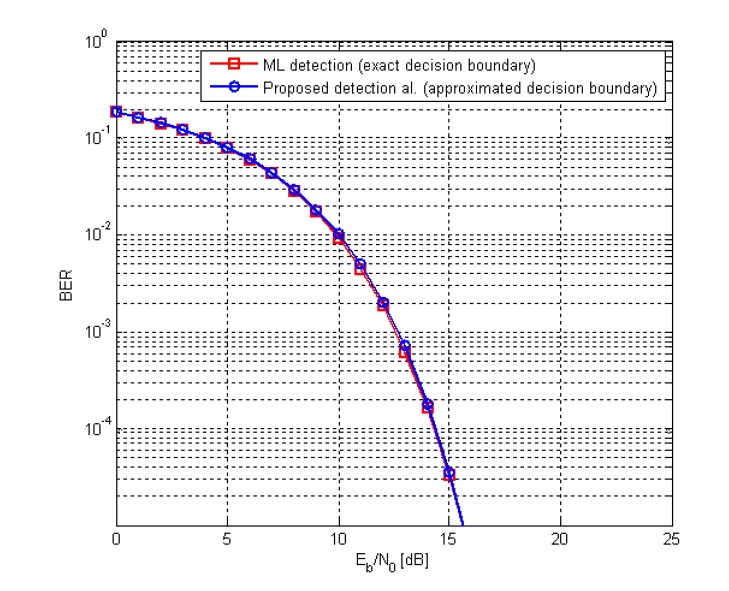
Fig. 7 shows the BER performance of the 4+12+16 APSK over the nonlinear AWGN channel and Fig. 8 shows the change of TD depending on IBO. As shown in Figs. 7 and 8, the newly proposed bit mapping has the better performance by about 0.2 dB than the bit mapping in the DVB-S2 standard when IBO is 9 dB at the BER of 10^-5 and the total power degradation decreases by about 0.7%. Note that the performances of the bit mapping suggested by Kim et al. (2007) and the bit mapping proposed in this paper are similar. Fig. 9 shows the BER performance of maximum likelihood (ML) detection using exact decision boundary and that of the proposed bit detection algorithm using the approximated decision boundary in the linear AWGN channel. As can be known from the Fig. 9, the BER performance of the simple bit detection algorithm proposed in this paper is almost the same with that of ML detection using exact decision boundary.

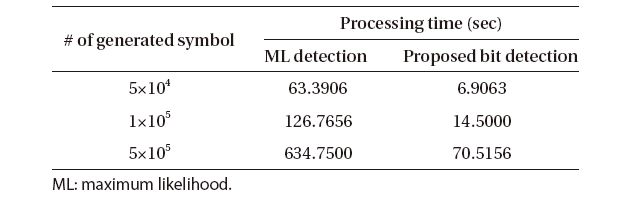
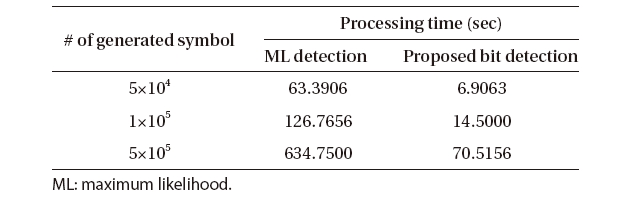
Since ML detection in AWGN channel is to find out the reference signal which is closest to the received symbol (Proakis 2001), the distances with all the 32 signal points should be calculated to detect the five bits (b_i, i = 1, 2, ..., 5) implied in one received symbol. That is, 64 square calculations are required to detect the five bits. In the newly proposed algorithm, however, the only simple comparisons among the amplitudes or phases are used to detect the five bits implied in one symbol. The processing time

of ML detection and that of the newly proposed bit detection algorithm are compared in Table 1. As indicated in Table 1, less processing time is required for the proposed bit detection algorithm than that for ML detection. Consequently, the new bits-to-symbol mapping proposed in this paper can reduce the signal processing time and power consumption in a receiver side since it has a better performance in nonlinear channels and allows a simpler receiver design.

In this paper, we proposed the new bits-to-symbol mapping scheme where the bits are mapped so that the Hamming distances between the signal points with the small Euclidean distance by nonlinear distortion of HPA in the transmitter with 4+12+16 APSK can be minimized. For this, the change of the signal constellation due to the HPA nonlinear characteristics was firstly analyzed. Based on the analysis, a new bit mapping scheme for the 4+12+16 APSK in the nonlinear AWGN channel was developed. We have also verified from the BER analysis that the BER performance of the newly proposed bit mapping is a better than that of the bit mapping in the DVB-S2 standard. Particularly, it was verified through the newly proposed simple signal detection algorithm that the newly proposed bit mapping can reduce the burden of the receiver during signal detection since the mapping structures of more bits are symmetric on the I/Q axis when compared with the conventional bit mappings. The region based mapping method used to obtain the proposed bit mapping can be applied not only to the 4+12+16 APSK but also to other 32-APSK modulation schemes. In addition, the proposed bit mapping is expected to be well applied to the systems using the HPA and the systems sensitive to power consumption since it shows a better performance to the HPA nonlinear distortion and allows simpler receiver design.