In recent years, the US, EU, Japan, China, and India push to drive the outer space missions, especially lunar missions, which notifies that the round two of space race has just begun. Therefore, numerous lunar missions are under execution or newly programmed. Related missions are ESA’s SMART-1 (Foing et al. 2006), JAXA’s SELENE (Kato et al. 2008) and SELENE-II (Tanaka et al. 2008), CNSA’s Chang’E (Zheng et al. 2008), ISRO’s Chandrayaan- 1 (Goswamia & Annaduraib 2008) and NASA’s LRO (Chin et al. 2007). As for the current issues in lunar explorations, the possibility of the Korean space program exploring outer planets is now under consideration. The Korean government announced that Korea will launch its first lunar orbiter by 2020 and will attempt to land by 2025. In addition, the government has already assigned to join the U.S.-led International Lunar Network. Therefore, the design studies for future lunar missions are recently emphasized and actively discussed in astronauti cal society of Korea.
For an Earth-Moon transfer trajectory with impulsive high thrust, Song et al. (2008b) developed the lunar mission design software, and designed the optimal Earth-Moon transfer trajectory. For lunar injection conditions, Song et al. (2008b) assumed direct departure from circular initial Earth parking orbit. Later, Song et al. (2009) presented various optimal Earth-Moon transfer trajectories using intermediate Earth departing loop orbits by upgrading the previously developed lunar mission design software. In the literature by Song et al. (2009), spacecraft’s visibility analysis from Daejeon ground station is also made, but considered only visibility conditions while executing the trans lunar injection (TLI) maneuver. They found that there exist slight differences in total delta-V magnitude if the spacecraft’s visibility is guaranteed while executing the TLI maneuver. As the lunar orbit insertion (LOI) maneuver is also another crucial maneuver to conduct a lunar mission successfully, it is necessary to design the optimal lunar transfer trajectory not only guaranteeing the visibility conditions at the TLI maneuver time but also at the LOI maneuver time from a specified ground station. Although the explorer’s flying status can be tracked with the help of Deep Space Network (DSN), in practical mission operation for future Korea’s lunar mission, securing the spacecraft’s visibilities from Daejeon ground station while executing these two important maneuvers (both the TLI and LOI) have important meanings. As the exact status of spacecraft is obtained rapidly, despite of unpredicted errors are occurred, the better mission backup plans would be readiness (i.e., trajectory correction maneuver plans).
Therefore, the current study has the purpose to design the optimal lunar trajectory considering the visibility of spacecraft from the Daejeon ground station at both the TLI and LOI maneuvers. To simulate and analyze the optimal Earth-Moon transfer trajectory as discussed, the Korean Lunar Mission Design Software using Impulsive high Thrust Engine (KLMDS-ITE) software which was developed in the previous studies (Song et al. 2008b, 2009) is modified. Using the modified KLMDS-ITE software, the optimal lunar transfer trajectory is designed from the Earth departure to the final LOI phases. Minimum energy transfer trajectory solution is derived, and also the spacecraft’s visibility from Daejeon ground station at both the TLI and LOI maneuvers are guaranteed by applying additional visibility constraints. By applying these additional visibility constraints, the Earth-Moon transfer trajectory guaranteeing visibilities from both at the TLI and LOI maneuvers could be designed with no help of additional trajectory correction maneuvers.
The equations of motion used to derive optimal trajectory solution include: perturbing forces due to the point masses of the Earth, Sun and Moon and also, Earth’s J2 effects. Additionally, the Lambert method and B-plane targeting method are applied during the trajectory optimization process. In the following discussions, various simulations are performed and trajectory design results are analyzed. The influences of the visibility constraints at both the TLI and LOI maneuvers are also investigated to see how they affect to the overall mission delta-V magnitudes as well as the trajectories characteristics. In the Section 2, optimal trajectory design strategy is discussed with the brief algorithm flows of modified KLMDS-ITE software. The Section 3 provides detailed simulation results for derived optimal trajectory solutions as well as the initial conditions, the performance index, and final constraint conditions for given problem. Finally, in the Section 4, conclusions are made. The results provided in this paper are expected to make further progresses to Korea’s future lunar mission planning area, as for proposing the more advanced practical design results with regarding the operational conditions from the Daejeon ground station.
2. OPTIMAL TRAJECTORY DESIGN STRATEGY
In general, there exists four different mission phases for a given lunar mission. First, a spacecraft performs a TLI maneuver to insert a spacecraft from the Earth parking orbit to the trans-lunar trajectory. Second, after a TLI maneuver, a spacecraft coasts along in the trans-lunar trajectory. Third, a spacecraft performs a LOI maneuver to be captured into the Moon. Finally, a spacecraft performs several de-orbit maneuvers, usually called apoapsis adjustment maneuvers (AAMs), to change its orbit from the captured orbit to a desired mission operational orbit at the Moon. The design study for the optimal lunar mission trajectory should be conducted with including these four different mission phases, as most of the mission budgets are determined by magnitudes of the TLI and LOI maneuvers. These two big major maneuvers are the most crucial factors to conduct a lunar mission successfully. In the same context, securing the visibility of spacecraft from the specified ground station at executing the TLI and LOI maneuvers is another important parameter which has to be considered at the initial mission design stage; for easy and rapid confirmations weather these two maneuvers are successively executed or not.
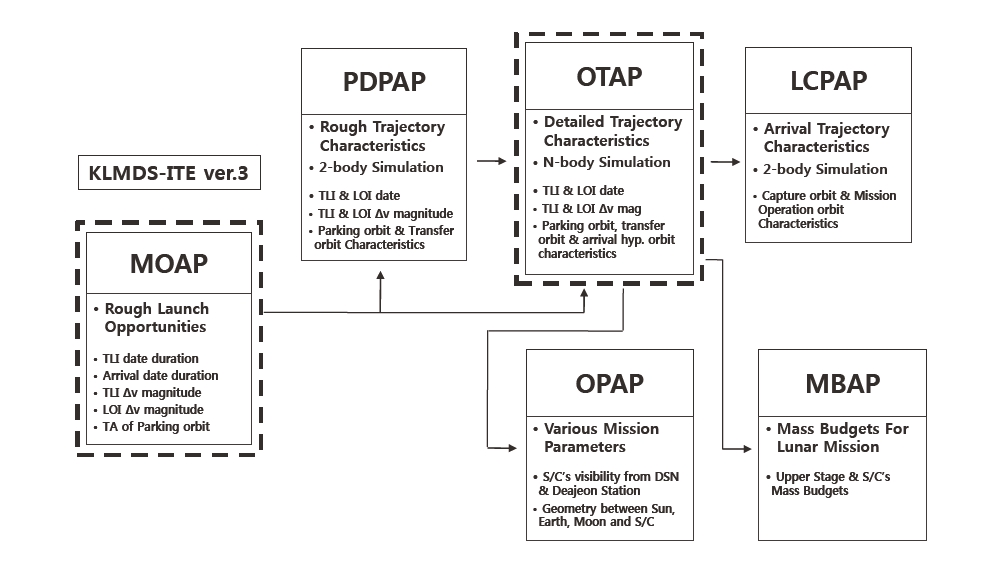
To simulate and analyze the optimal Earth-Moon transfer trajectory considering the visibility of spacecraft from Daejeon ground station at both the TLI and LOI maneuvers, the KLMDS-ITE is modified. The KLMDS-ITE software was developed by Song et al. (2008b) with the purpose of designing and analyzing Korea’s future lunar mission trajectory. The developed KLMDS-ITE software consist of six different functional modules (mission opportunity analysis program [MOAP], preliminary design parameter analysis program [PDPAP], optimal trajectory analysis program [OTAP], operation parameter analysis program [OPAP], lunar captured phase analysis program [LCPAP], and mass budget analysis program [MBAP]) to design every lunar mission phases. Although these six different modules have different functional aspects, they are closely related to each other for its effectiveness. Among the six different modules in the KLMDS-ITE software, only two modules (MOAP and OTAP) are modified to include the spacecraft’s visibility constraint from Daejeon ground station at both the TLI and LOI maneuvers. Therefore, the modified KLMDS-ITE software still has six different functional modules, and their different functional roles are summarized as following. Also, the brief algorithm flows and the main functions of the each modified KLMDS-ITE’s modules are shown in Fig. 1.
The MOAP module finds the launch window considering the characteristics of the Earth parking orbit. Input parameters for this module are the altitude, eccentricity and inclination of the Earth parking orbit, the time of flight (TOF) of the trans-lunar trajectory. Using the MOAP module, users can approximate the launch window, magnitude of the TLI maneuver, the parking orbit’s argument of latitude at TLI maneuver, and the incoming v-infinity velocity at the Moon. The incoming v-infinity velocity at the Moon (V∞) can be derived by subtracting the Moon’s orbital velocity from the spacecraft’s velocity in the Earth centered inertial (ECI) coordinate system. Users can select the best launch window (injection opportunities), where both the magnitude of the TLI maneuver and the incoming v-infinity velocity’s magnitudes show the minimum values, by analyzing the ‘contour plot’ generated by this module. In the MOAP module, the launch window is computed with assumptions that the elevation angle of spacecraft is more than 8 deg at both the TLI and LOI maneuvers, then the spacecraft is visible from the Daejeon ground station. The spacecraft’s visibility conditions from a specified ground station at the LOI maneuver is closely related to the Moon’s elevation angle, and the Moon’s elevation angle itself is again related to the Moon’s rise and set time from the specified ground station. Therefore, the spacecraft’s visibility conditions at the LOI maneuver can be secured by adjusting
the mission’s TOF, which is related to the spacecraft’s arrivaltime at the Moon.
The second module, PDPAP roughly analyzes the characteristics of the optimal Earth parking orbit and the Earth-Moon trajectory by using the 2-body problem with the well-known Lambert theory. Input parameters for this module are orbital elements of the initial Earth parking orbit; altitude (
With the performance index described in Eq. (1), minimum energy Earth-Moon transfer trajectory solutions with simple dynamics can be obtained. The control parameters for the PDPAP module are given to have the TLI maneuver time (TΔVTLI), and the true anomaly (υprk) of the parking orbit at that TLI maneuver time. The SNOPT (Gill et al. 2002) is used to find the optimal trajectory solution for given nonlinear problem. Roughly approximated initial Earth parking orbit as well as Earth-Moon transfer trajectory solutions can be obtained using this PDPAP module.
The OTAP module determines the precise optimal lunar trajectory including perturbing forces due to the point masses of the Earth, Sun and Moon and also, Earth’s J2 effects. Unlike PDPAP module, the concept of B-plane is adapted in this module and the final lunar closest approach conditions are achieved with the B-plane targeting method. Input parameters for OTAP module are almost same as PDPAP module, however several additional input parameters are required; each vector component of the TLI maneuver (ΔVTLI_X,ΔVTLI_Y,ΔVTLI_Z), right ascension of ascending node (Ωprk) of the initial parking orbit, the TOF (TTOF), and lower and upper boundaries for these parameters. In addition, target orbit’s altitude (
where 'ΔVTLI' has the same meaning as defined in Eq. (1), however 'Vhyperapp' denotes the lunar closest approach hyperbolic velocity at perilune which is determined during the B-plane targeting process. Setting the performance index as shown in Eq. (2) is directly related to the problem of minimizing the overall delta-Vs (from Earth departure, TLI, to the final lunar orbit insertion, LOI and AAMs) required to complete the lunar mission. As required delta-Vs to achieve final target orbit at the Moon can just be derived by subtracting orbital velocities between the closest approach hyperbolic and target orbit’s velocity at perilune, minimizing 'Vhyperapp' has the same meaning as that of minimizing required delta-Vs to achieve final target orbit under same perilune altitude conditions. In addition, under same perilune altitude, total number of capturing orbit used to achieve final target orbit have no effects to required overall delta-V magnitude changes, a simple orbital energy conservation theory, as shown in previous literature by Song et al. (2009). As like PDPAP, the SNOPT (Gill et al. 2002) is used to find the optimal trajectory solution for given nonlinear problem. The control parameters for the OTAP module are given to have, TLI maneuver time (TΔVTLI), and the true anomaly (υprk) and right ascension of ascending node (Ωprk) of the parking orbit, each vector component of the TLI maneuver (ΔVTLI_X,ΔVTLI_Y,ΔVTLI_Z) and the TOF (TTOF), was also considered as an another control parameter during the B-plane targeting process to secure the spacecraft’s visibility conditions at the time of LOI maneuver as well as to aim the target point precisely. The results derived from the PDPAP module can be used as initial guesses for the OTAP module’s input parameters to ease the sensitivity problem which may occur during the initial guessing procedures. As the OTAP module utilizes the concept of B-plane to precisely target the aim point at the lunar closest approach, final equality conditions are given with the concept of B-plane and the flight path angle condition. Although detail procedures to derive these equality constraints are omitted in this paper, details about the B-plane targeting method have been treated in numerous literatures (Kizner 1961, Sergeyevsky et al. 1983, Kemble 2002, Song et al. 2005). For inequality constraints, the elevation angle of the spacecraft seen form the Daejeon ground station should be more than 8 deg at both the TLI and LOI maneuvers’ executions, are given to secure the spacecraft’s visibility conditions. Therefore, correspond to the visibility constraints, the OTAP module acquire the detailed characteristics of the optimal Earth-Moon transfer trajectory, the TOF, and both the TLI and LOI maneuvers’ characteristics that guarantee the spacecraft’s visibility conditions form the Daejeon ground station.
The LCPAP module calculates the every velocity changes that spacecraft requires to be captured into the final mission operational orbit. These velocity changes include a LOI maneuver and several de-orbit AAMs. With the user provided intermediate orbits’ sequence near the Moon, the LCPAP modules derives the LOI maneuver characteristics and other several de-orbit AAMs to achieve final mission operational orbit. Usually, several intermediate orbits are given to be as elliptical orbit and final mission orbit is given as a circular orbit. After the spacecraft is inserted into the final lunar mission orbit, the ground track of the spacecraft seen from a surface of the Moon is obtained by converting the spacecraft’s states into the lunar centered lunar fixed (LCLF) coordinate system. In this module, the total magnitude of velocity changes (LOI + AAMs) required during lunar capturing sequences is also calculated.
The OPAP module computes other mission parameters which have important meanings at initial mission scoping studies. In this module, the Earth ground track is calculated to check the position of the spacecraft during both the TLI and LOI maneuvers. With the OPAP module, user can analyze the spacecraft’s visibility conditions from the DSN (located at the Goldstone, Canberra and Madrid) as well as the Daejeon ground station. The relative geometries between the Earth, Moon, Sun, and the spacecraft are also provided in this module to give a direction of the solar panel of the spacecraft, and to investigate the eclipse time.
The MBAP module calculates various mass budgets for a given lunar mission. Mass budgets include the kick motor’s fuel mass which is usually required for TLI maneuver, the spacecraft’s own fuel mass for the LOI maneuver and AAMs. The spacecraft’s dry mass is also calculated with regarding launch vehicle’s maximum on-orbit capability. Every mass budgets derived in this module utilize the results from OTAP module, various minimized delta-Vs’ magnitudes, which leads the fuel masses to be minimized. More details of these six different functional modules can be found at works by Song et al. (2008b, 2009).
In the current study, the optimal Earth-Moon transfer trajectory is derived which considered the spacecraft’s visibility from the Daejeon ground station at executing both the TLI and LOI maneuvers. For numerical simulations, the initial Earth departure orbit is set to be same as used in the previous study (Song et al. 2009). Among the various Earth departing conditions studied in Song et al.’s (2009) work, direct departure from the initial circular Earth parking orbit (with inclination of 80 deg and an altitude of 300 km) is selected to see the effect due to the spacecraft’s visibility constraints at executing both the TLI and LOI maneuvers. Also, as like in Song et al.’s (2009) work, the Korea Space Launch Vehicle-2 (KSLV-2) is assumed as the launch vehicle with capability of launching about 2.6 tons (including spacecraft and upper stage’s kick motor for TLI maneuver) and kick motor’s Isp (287 seconds) and structure ratio (0.152) are considered as same as in previous literature by Song et al. (2008a). If the Earth departing orbit is selected to have various intermediate loop orbits, and if the spacecraft’s visibility from the Daejeon ground station should be secured while executing several orbit raising maneuvers to achieve intermediate loop orbits, then the trajectory analysis must be performed with different ways.
For lunar capturing sequences in this study, Lunar Prospector’s lunar capturing sequences are adapted to achieve the final mission operational orbit at the Moon. The first elliptical lunar capture orbit for the Lunar Prospector had about 12 hour orbit, the second had about 3.5 hour orbit, and the third about 117.849 minutes, respectively. The final mission operational orbit was a 90 deg inclined circular polar orbit with an altitude of 100 km (Lozier et al. 1998). It is also assumed that Korea’s fictitious lunar mission is planned to inject the spacecraft into a trans-lunar trajectory on 2017-2-15 and spacecraft’s on board Isp is assumed to be 300 seconds as like in previous study done by Song et al. (2009) to directly compare the results. However, injection opportunities at any other date could be easily investigated using the developed algorithm.
3.1 Injection opportunity analysis
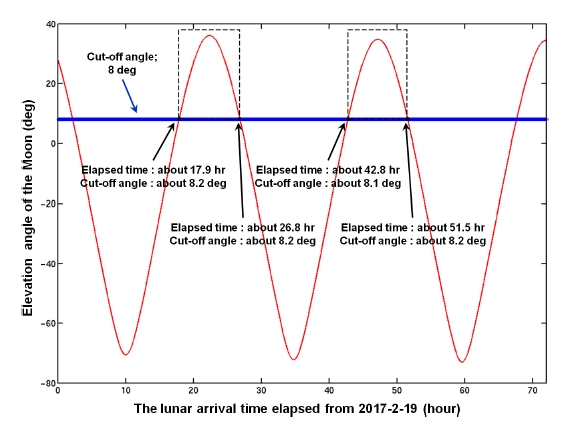
The spacecraft’s injection opportunities around 2017-2-15 are investigated using the modified MOAP module with considering spacecraft’s visibility from the Daejeon ground station at both the TLI and LOI maneuvers. Before investigating the spacecraft’s injection opportunities, the Moon’s visibility conditions from the Daejeon ground station are checked. The Moon’s visibility condition from the Daejeon ground station, when the spacecraft arrived at the Moon, will certainly secure the spacecraft’s visibility conditions at time of the LOI maneuver. Fig. 2 shows the visibility conditions of the Moon from the Daejeon ground station at various lunar arrival time. To plot Fig. 2, it is assumed that the spacecraft is injected into a trans-lunar orbit at 2017-2-15 00:00:00 with 4∼7 days of TOF. Thus, the spacecraft’s arrival time at the Moon is around 2017-2-19∼2017-2-22. As seen from the Fig. 2, there exist only two possible time areas where the Moon is visible from the Daejeon ground station; after about 18∼27 and 43∼51 hours since 2017-2-19. Therefore, it can be estimated that TOF should have about 4.5 ± 0.2 days or 5.5 ± 0.2 days to guarantee the spacecraft’s visibility
visibility conditions from the Daejeon ground station at the time of LOI maneuver.
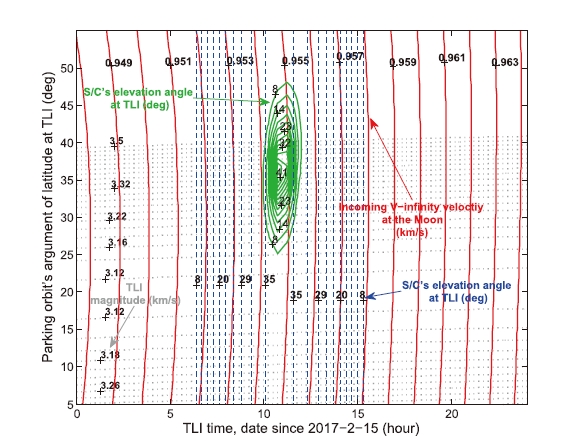
As we have roughly estimated the TOF to secure the spacecraft’s visibility at lunar arrival, lunar injection opportunities are then investigated using the modified MAOP module. Fig. 3 shows the contour plots which can analyze the injection opportunities. In Fig. 3, it can be easily noticed that additional mission parameter, the spacecraft’s elevation angle at the LOI maneuver, is included which did not presented in previous study by Song et al. (2009). Fig. 3 is obtained with TOF of about 4.48 days which is in boundaries of TOF (4.5 ± 0.2 days) previously estimated. With regarding the Daejeon station’s visibility, Fig. 3 shows that the best TLI maneuver opportunity occur about 9±12.5 hours since 2017-2-15. After about 4.48 days of flight, it can be again easily noticed that the spacecraft’s visibility conditions are also secured from the Daejeon station by checking the spacecraft’s elevation angle conditions at the LOI maneuver. For this injection opportunities, the corresponding parking orbit’s argument of latitude is about 24±35 degs, the TLI maneuver’s magnitude is about 3.14±3.40 km/s, and the lunar approach hyperbolic velocity is about 0.954±0.956 km/s.
Using the results from the modified MAOP and PDPAP module, more detailed optimal Earth-Moon transfer trajectories are simulated by the modified OTAP module. When good enough initial guesses, which could be only found by after numerous trial errors, are provided for different control parameters in OTAP module, the time required to derive the optimal trajectory solution using the SNOPT was about 2.6 minutes. Optimal trajectory solutions obtained from the modified OTAP module is re
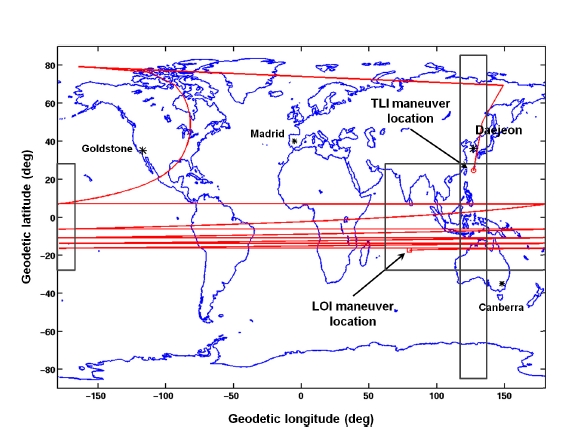
ferred as the Case 1 in following subsection. Fig. 4 shows the Earth ground track for an Earth-Moon transfer trajectory derived with OPAP module with solution of the Case 1. In Fig. 4, locations for both the TLI and LOI maneuvers are laid inside of boxed areas, which indicate the Daejeon ground station’s visible boundaries for the TLI and LOIs’ maneuvering time.
3.2 Case studies for different visibility conditions
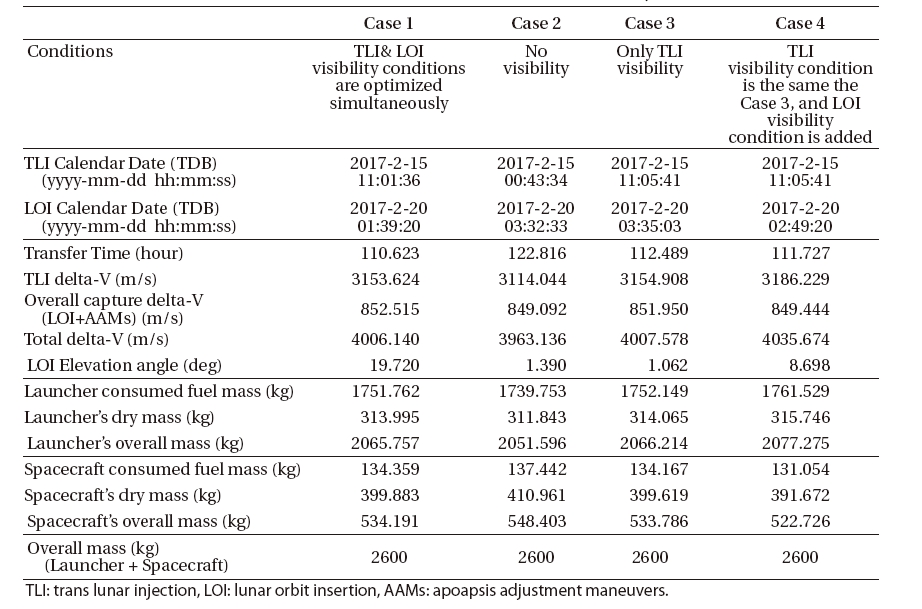
In this subsection, four different mission scenarios having different visibility conditions are established and analyzed. As discussed at the previous subsection, the Case 1 is optimized with considering the spacecraft’s visibility from the Daejeon ground station at both times of the TLI and LOI maneuvers. For the Case 2, none of the visibility conditions are considered. The Case 3 is with the visibility constraint at only time of TLI maneuver. For the Case 4, initial spacecraft’s states and TLI maneuver time are the same as those of the Case 3 to maintain visibility condition at the time of TLI maneuver, but the LOI visibility constraint is added. In Table 1, the results and characteristics of each case are compared. Every fuel masses described in Table 1 are derived using MBAP module, based on the results from optimized delta-Vs magnitudes by OTAP module. They indicate the least requirements on fuels which were derived with no margins on minimized delta-Vs. However, if some margins on minimized delta-Vs are considered, these fuel masses could be slightly changed. In Table 1, it can be easily noticed that launcher and spacecraft’s overall masses (fuel + dry) are different though they had the same initial launch vehicle’s capability of launching about 2.6 tons. These phenomena are due to that the minimized magnitudes for TLI and overall lunar capture delta-Vs (LOI+AAMs) are different for each simulation case. The magnitude of TLI burn firstly determines the launcher’s fuel mass, and together with already determined (fixed) launcher’s dry mass, launcher’s overall mass could be easily determined. Then the maximum spacecraft’s overall mass (fuel + dry), which could be delivered to the Moon, can be derived just subtracting the computed launcher’s overall mass from the launch vehicle’s maximum on-orbit capability. However, required spacecraft’s fuel masses for successful lunar insertions are differ for each case, since overall lunar capture delta-Vs’ (LOI+AAMs) magnitudes are different to each other.
Let us begin with analyzing the Cases between 2 and 3. As already discussed by Song et al.’s (2009) work, constraining the TLI maneuver’s location to secure the spacecraft’s visibility conditions from the Daejeon ground station would require more TLI delta-V. In this
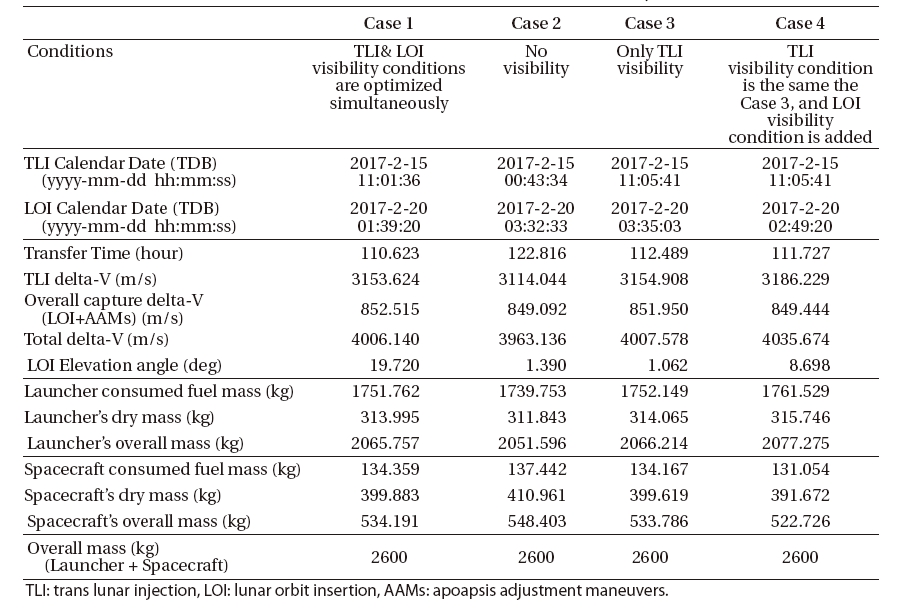
Results and characteristics comparison for each case with different visibility conditions. The initial Earth departure parking orbit is circular with an altitude of 300 km, 80 deg of inclination and the final mission operational orbit is a circular polar orbit (90 deg inclined) with an altitude of 100 km at the Moon for every cases.
simulation, like previous work by Song et al. (2009), TLI maneuver’s magnitude between the Cases 2 and 3 resulted up to about 1.3% difference; about 3,114 m/s for the Case 2, about 3,155 m/s for the Case 3. For overall mission delta-Vs, including maneuvers required in lunar capturing sequences, about 1.1% of delta-V’s difference is observed. More detailed discussions for the reasons of these phenomena can be found at works by Song et al. (2009). As current study is focused to investigate the optimal Earth-Moon transfer trajectory’s characteristics when the spacecraft’s visibility is guaranteed at both times of the TLI and LOI maneuvers, the Case 4 is additionally simulated. Once again, for the Case 4, initial spacecraft’s states and TLI maneuver time are the same as those of the Case 3 to maintain visibility condition at the time of TLI maneuver, but the LOI visibility constraints are added during the trajectory optimization process.
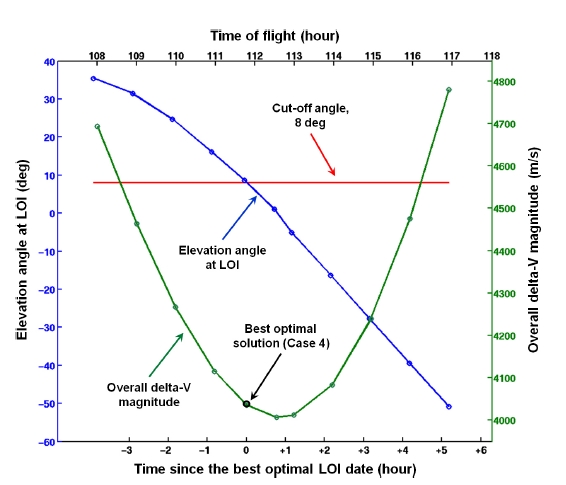
Although the TLI maneuver’s execution time and the spacecraft’s initial states are remained same between the Cases 3 and 4, the additional constraint to secure the spacecraft’s visibility at the time of LOI maneuver resulted in different transfer time (about 112.5 hours for the Case 3, about 111.7 hours for the Case 4), different TLI magnitude (about 3,155 m/s for the Case 3, about 3,186 m/s for the Case 4), and different total mission delta-V’s magnitude (about 4,008 m/s for the Case 3, about 4,036 m/s for the Case 4). The results for the Case 4 are found to be as the optimum case and the spacecraft’s visibility is secured from the Daejeon ground station at the time of LOI maneuver with elevation angle about 8.7 deg. Con
Consequently,about 0.7% of more overall delta-V is required than the Case 3.
As it has shown that the spacecraft’s visibility condition at the time of LOI maneuver is strongly related to the mission’s TOF, another set of simulation is performed to see the effects of different TOFs on mission parameters. For this simulation, like the Case 4, initial spacecraft’s states and TLI maneuver time are remained to be same as those of the Case 3, but the LOI visibility constraint is
Let’s compare the trajectory solutions between Cases 1 and 3. As discussed, the Case 1 is solution optimized with considering the spacecraft’s visibility from the Daejeon ground station at both times of the TLI and LOI maneuvers. The Case 3 is with the visibility constraint at only the time of TLI maneuver. Interestingly, the TLI maneuver time and the characteristics of the Earth parking orbit are very similar in these two cases. The magnitude of the total delta-Vs has a difference about 0.036% between the Case 1 (about 4,006 m/s) and the Case 3 (about 4,008 m/s). Therefore, spacecraft’s mass which can delivered to the Moon has only about 0.4 kg of difference (Case 1 is about 534.2 kg and Case 3 is about 533.8 kg). Various mission parameters for these two cases are well compared in Table 1. With this comparison result, it can be concluded that constraining the spacecraft’s visibility at the time of LOI maneuver has a minor effect in changes of over-all mission delta-Vs than constraining the spacecraft’s visibility at the time of TLI maneuver. It is clearly shown that the constraining spacecraft’s visibility condition at the time of LOI maneuver is closely related to the mission’s TOF. Also, slight changes in initial Earth departing conditions (TLI maneuver’s time, injecting location at the Earth parking orbit and TLI maneuver’s magnitude) changes mission’s TOF as well as the lunar arrival time. Therefore, to minimize overall delta-Vs, the spacecraft’s visibility constraints at both the TLI and LOI maneuvers should be simultaneously implemented to the trajectory optimization algorithm. It is rather general phenomena that the spacecraft’s visibility conditions at the both times of TLI and LOI maneuvers are strongly co-related to every mission parameters: TLI maneuver’s time, magnitude and location, mission’s TOF, LOI maneuver’s time and location, etc. Thus, proper combinations of these parameters could result the optimal Earth-Moon transfer trajectory, without major changes in total amount of mission delta-Vs, which satisfies the spacecraft’s visibility conditions from the Daejeon ground station at both times of the TLI and LOI maneuvers.
In the current study, the optimal Earth-Moon transfer trajectory considering Daejeon ground station’s visibility at both the TLI and LOI maneuvers is designed. As a result, it is found that the optimal Earth-Moon transfer trajectory, guaranteeing the spacecraft’s visibility from Daejeon ground station at both the TLI and LOI maneuvers, can be designed with slight changes of total mission delta-Vs. About 1% difference is observed with the optimal trajectory when none of the visibility condition is guaranteed, and about 0.04% difference with the visibility condition is guaranteed only at TLI maneuver. The spacecraft’s mass which can be delivered to the Moon for these cases are: about 548 kg (fuel: 137 kg + dry: 411 kg) when none of the visibility condition is considered, about 534 kg (fuel: 134 kg + dry: 400 kg) when the visibility condition is guaranteed at only time of TLI maneuver, and finally, about 534 kg (fuel: 134 kg + dry: 400 kg) again, when the spacecraft’s visibilities are guaranteed at both the TLI and LOI maneuvers. From practical point of view, the spacecraft’s visibility constraints at both the TLI and LOI maneuvers should be simultaneously implemented to the trajectory optimization algorithm. Since proper combinations of various mission parameters could result the optimal Earth-Moon transfer trajectory, without major changes in total amount of mission delta-Vs, which satisfies the spacecraft’s visibility conditions from the Daejeon ground station at both times of the TLI and LOI maneuvers. The results provided in this paper are expected to make further progresses to Korea’s future lunar mission planning area, as for proposing the more advanced practical design results with regarding the operational conditions from the Daejeon ground station.