Johann Daniel Titius von Wittenberg first attempted in 1766 to representat planetary distances with an empirical relation giving the semi-major axis
where
Titius-Bode’s relation embarrassingly breaks down for Neptune and objects farther than that,while it gives neat results for the eight first planets, including the asteroids. This is where peoplebegin to doubt Titius-Bode’s relation. Moreover, most of researchers do believe that there is nophysical basis to explain the apparent simple mathematical relation between distances of naturalbodies revolving around a central body, though several theories of the solar system formation haveattempted to account for these distance relations (Dermott 1972, 1973, Dob´o 1981, Louise 1982,Llibre & Pin?ol 1987, Patton 1988, Graner & Dubrulle 1994a,b, Li, Zhang, & Li 1995, Nottale,Schumacher, & Gay 1997, Ortiz et al. 2007). Attempts from other directions to explain the origin ofthe relation have been also made. For instance, some authors have sought to find a solution amongrandom processes (e.g., Lecar 1973, Pletser 1988, Hayes & Tremaine 1998, Nesluˇsan 2004).
The question of whether the observed patterns have some physical reasons or are due to chancemay be addressed using a Monte Carlo approach. Lynch (2003), however, finds that the estimatedprobability of chance occurrence depends sensitively on restrictions imposed on the population oforbits. Another strategy to pursue is testing whether Titius-Bode’s relation is exclusively applicableto our own Solar system. If it is not the case, it would indirectly demonstrate that Titius-Bode’srelation is more than pure numerological speculations and to be understood. In fact, Titius-Bode’srelation has been recently tried to exo-planetary systems. For instance, Vahia, Mahajani, & Rao(2003) have investigated the distribution of extrasolar system planets to search for periodicities intheir distribution around their parent star. More recently, Poveda & Lara (2008) have investigated ifthe exo-planetary system, 55 Cancri (= HD 75732), fits some form of Titius-Bode’s relation.
In this paper, we study the distribution of period ratios of two planets in multiple planet systems by comparing it with that derived from not only Titius-Bode’s relation but also other forms of it. According to Kepler’s 3rd law and to a generalized Titius-Bode’s relation, i.e., an χ
This paper begins with descriptions of the distribution of the ratio we analyze and data of exoplanetary systems in section 2. We present results obtained with χ2 test in section 3. Finally, we discuss and conclude in section 4.
2. Distribution of Ratio of Orbital Periods
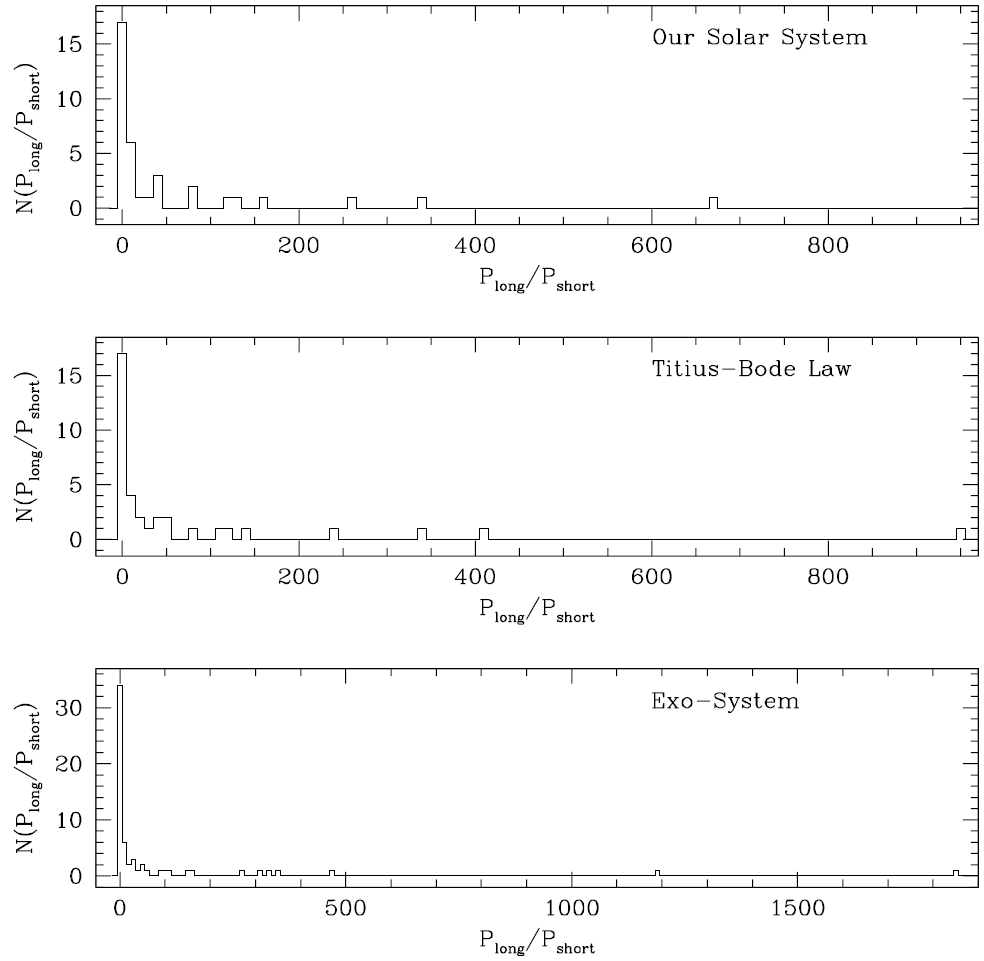
In Figure 1, we show the distribution of period ratios of two planets. In the top panel, the distribution of the ratio of observed periods of two planets in our solar system is shown. To obtain the ratio we randomly choose two different planets and take the ratio such that the value is always greater than unity. It should be noted that we do not consider Pluto (
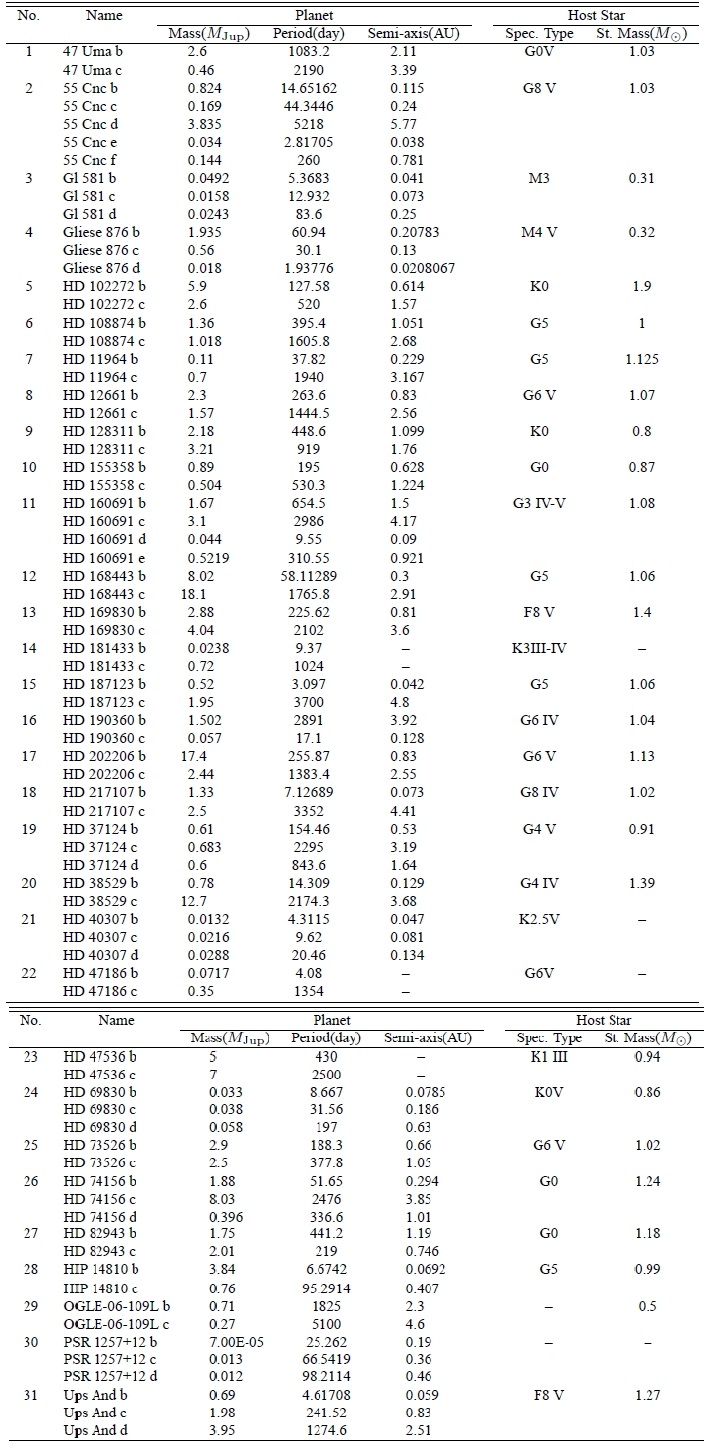
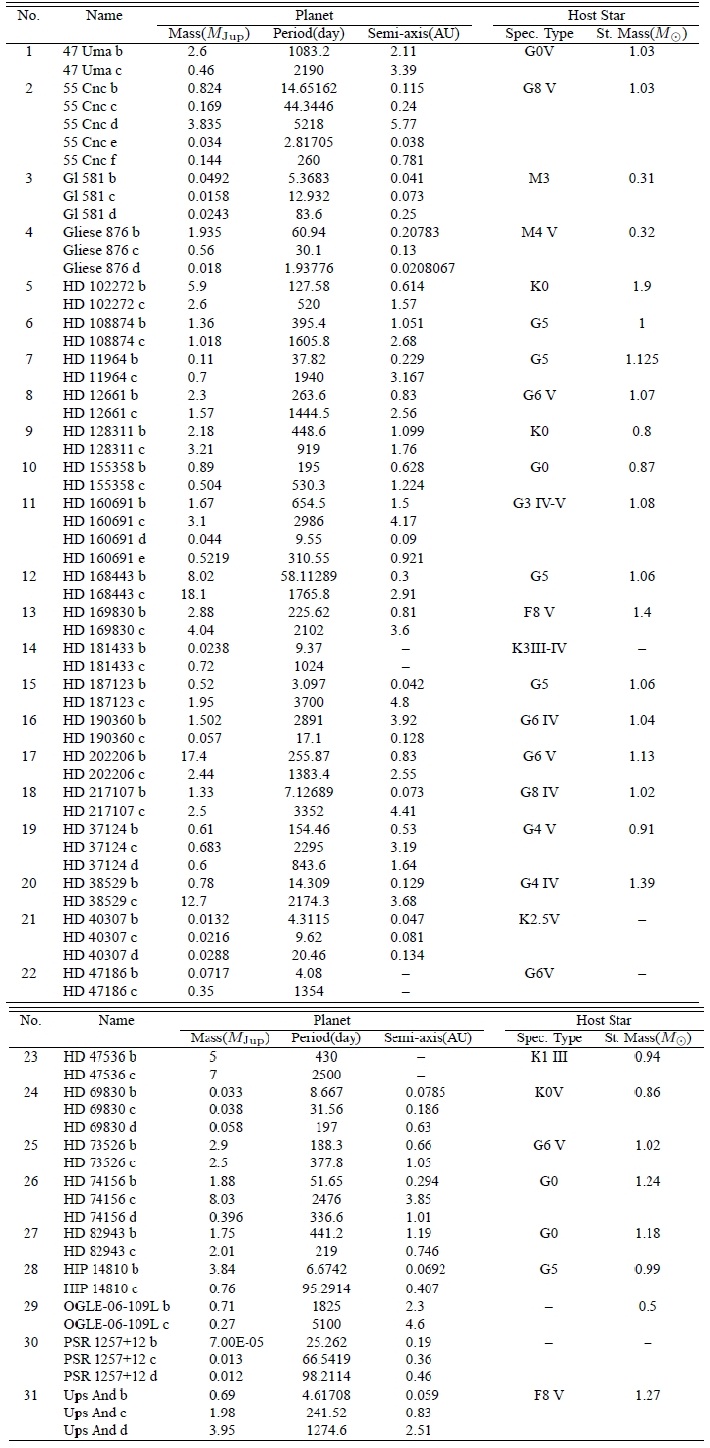
Multiple planet systems adopted in the present analysis. Data of planets and host stars are taken fromthe Extrasolar Planets Encyclopedia.
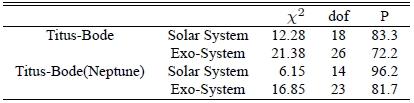
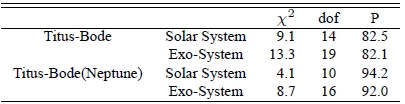
We perform a statistical test to check if the observed ratio distributions are consistent with that derived from Titius-Bode’s relation, by calculating χ2 values between two binned distributions resulting from the ratio of the orbital period. In Table 2, we show the χ2 value with the degrees of freedom, dof, and probability that two data sets are drawn from the same distribution function. The size of bins is fixed to the same for all the cases throughout the analysis, i.e., 10. In the first row, results of the χ2 test between the distribution of the orbital period derived from Titius-Bode’s relation and that observed in our Solar system are shown. The χ2 value is 12.28 with high probability, i.e., 83.3 %. In the second row, the value of χ2 and probability resulted from Titius-Bode’s relation and observed exo-planetary systems are shown. The χ2 value is 21.38. The probability is 72.2 %. The probability is somewhat low, but not small enough to conclude that they are significantly different distributions. Hence, we tentatively conclude that the traditional Titius-Bode’s relation can be applied to exo-planetary systems. For comparison, in the third and fourth rows, we show results from Titius-Bode’s relation excluding Neptune are shown. As one may expect, the distribution derived from Titius-Bode’s relation rounded-off at Uranus should agree more satisfactorily with the distribution observed in our Solar system. Test results show that distributions are more consistent not only in the Solar system case but also in exo-planetary system case. We repeat same calculations with various bin sizes to see how robust our results are. Results of the χ2 test with other bin sizes also show they are comparable with reasonably high probability, i.e., higher than ≫ 80%, except the case of the Titius-Bode’s relation and the our solar system with Neptune. Two example cases of results are shown in Tables 3 and 4.
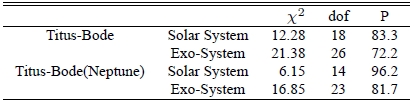
Results of the χ2 test. The first and second columns indicate the data set from which the distributionis derived. Values of χ2, the degrees of freedom, dof, and the probability, P, indicating two data sets are drawnfrom the same distribution function are listed in the third, fourth, and fifth columns, respectively.
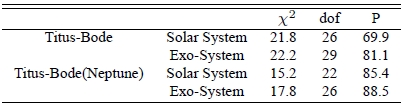
[Table 3.] Similar to Table 2, except that the adopted bin size is 5 instead of 10.
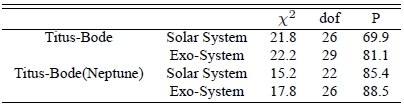
Similar to Table 2, except that the adopted bin size is 5 instead of 10.
[Table 4.] Similar to Table 2, except that the adopted bin size is 20 instead of 10.
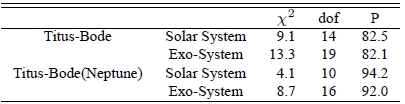
Similar to Table 2, except that the adopted bin size is 20 instead of 10.
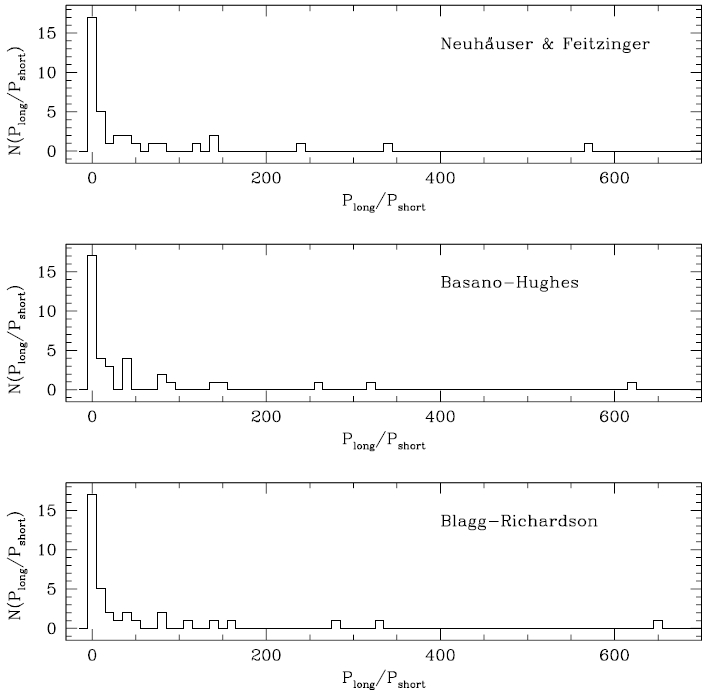
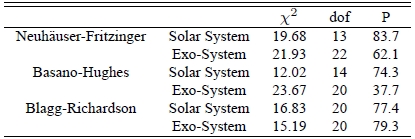
As we mentioned earlier, there are various versions of Titius-Bode’s relation. We also perform χ2 tests with those modified forms. In Figure 2, we show distributions of the calculated period ratio of two planets using other forms of Titius-Bode’s relation. Top panel is derived from Neuh¨auser & Feitzinger (1986), middle panel is from Basano & Hughes (1979), and bottom panel is from Blagg (1913) and Richardson (1945). Distance formulae are designated in the upper right corner of the panel. We include Ceres but omit Neptune and Pluto, as discussed in the Titius-Bode case. Results of the χ2 test are summarized in Table 5. Modified forms we adopted in this particular example in general agree with the planetary system as favorably as Titius-Bode’s relation does. The derived distributions are consistent with observed one in the Solar system with probability higher than ∼ 80 %, except the distance formula of Basano & Hughes (1979). Results of the χ2 test with the relation of Basano & Hughes (1979) become even worse in the case of exo-planetary system. It may reflect drawbacks of the relation (e.g., for further discussion on comparison of distance relations see Neuh¨auser & Feitzinger 1986).
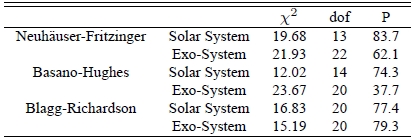
Similar to Table 2, except that various forms of Titius-Bode’s relations are tested as indicated. Results are from those excluding Neptune. Neuh¨auser-Fritzinger’s law is given as an = a + b × 2n, where a and b are given as a table determined with planets’ eccentricities, n is given by -?, 0, 1, and so on. Basano-Hughes’s law is given as an = 0:285 ×1:523n, where n runs from unity by one. Blagg-Richardson’s law is given as an = A £ 1:728n {B + f(α + nβ)g, where constants are determined empirically with a predetermined function, n is given by ¡2;¡1; 0; 1, and so on. See the text for references of the formulae.
1http://exoplanet.eu/catalog-all.php
We have examined whether Titius-Bode’s relation is also applicable to exo-planetary systems. For this purpose, we statistically study the distribution of observed orbiting period ratios of two planets in multiple exo-planetary systems by comparing it with that derived from various forms of Titius-Bode’s relation. As a result of the χ2 test we have carried out, one cannot rule out the possibility that the distribution of the ratio of orbiting periods in multiple planet systems is consistent with that derived from Titius-Bode’s relation. Having speculated Titius-Bode’s relation could be valid in exo-planetary systems, we tentatively conclude it is unlikely that Titius-Bode’s relation explains the distance distribution in our planetary system due to chance. It is, however, fair to point out a possibility that our finding is biased by the selection effect. In other words, most of extra-solar planets are detected by the radial velocity method which is sensitive to close and massive planets. One may think that this might have suppressed the distribution of period ratios at large Plong=Pshort, e.g., in Figure 1, since farther planets might be found less than would be. Or, at the same time, one may also think this might have enhanced the distribution of period ratios at large Plong=Pshort since closer planets might be found more than would be. The assumption we take in this analysis that the distribution of an ensemble from exo-planetary systems is approximately equivalent to that deduced by numerous random selections from a single planetary system should be resolved when large numbers of planets be found around many stars. We also admit that one may suggest that our conclusion is inconclusive in the sense that rigorous statistical tests should be carried out in terms of properties of host stars or parameters generating sub-samples.
If Titius-Bode’s relation of the solar system are more than pure numerological speculations, our finding has following implications. First one is on formation and evolution of the planetary system. The idea of planetary migration is prevalent in explaining hot Jupiters. Knowledge on the migration, such as, how to work, is found in the planetary disk dynamics. However, boundary conditions, for instance, where to start and/or to stop, is not coming from the first principle. We have no solidknowledge on the possible role of massive Jupiter-like planets in shaping up the distribution ofplanets. To this end, Titius-Bode’s relation may have some constraints. Another implication to bepointed out is on the extrasolar planet search. It seems that all the planetary systems own more thanone planet. Once a planet is found there is a chance to find another. Hence, it may help to discovernew planets by paying special attention to periodic signals in the radial velocities at values close tothe periods prediceted by Titius-Bode’s relation.