Thousands of satellites are now in operation for various purposes such as communication, navigation, military service, weather forecasting, and terrestrial and astronomical observations. Since satellite launches usually entail much cost and time, the social and economic cost that arises from satellite failure is critical. For satellite attitude control, reaction wheels, thrusters, and control momentum gyros are widely used as actuators. Therefore, the attitude control performance can be affected by actuator failure. If actuator failure occurs, the mission of the satellite cannot be accomplished or will be limited. Recently, the demand for satellite fault-tolerant control systems is increasing; therefore, considerable research has been undertaken that utilizes various control methods such as adaptive control, neural networks, sliding mode control, and so on (Henry, 2008; Jiang et al., 2008; Talebi and Patel, 2006; Tehrani et al., 2005; Wu and Saif, 2005). Tehrani used an estimator, based on neural networks, for fault diagnosis of the reaction wheel in a satellite attitude control system (Tehrani et al., 2005). Wu and Saif applied a sliding mode controller, based on neural networks, for satellite fault diagnosis (Wu and Saif, 2005). Henry used H-infinity and H_filter based schemes for the fault diagnosis of microscope satellite thrusters (Henry, 2008).

Several estimation and control schemes have been applied to deal with the failures of satellite systems. Especially, the iterative learning law is a fault estimation scheme for detecting and estimating faults. The iterative learning law using previous information can be applied to estimate both constant faults and time-varying faults (Chen and Saif, 2001, 2007).

In this paper, a fault tolerant control scheme with a modified iterative learning law is proposed to deal with the decreased effectiveness of satellite actuators. The modified iterative learning law using only information that is associated with the state error is adopted to estimate the influence of the actuator fault and the external disturbance. Lyapunov stability analysis is performed to obtain a stable controller. The performance of the proposed satellite attitude fault tolerant control scheme is verified by numerical simulations.

This paper is organized as follows. The second section describes the satellite system and the rest-to-rest maneuver of the satellite. In the third section, a fault tolerant controller with a modified iterative learning law is designed, and stability analysis is performed. In the fourth section, numerical simulations are performed to verify the performance of the proposed fault tolerant satellite control scheme. Finally, conclusions are drawn in the fifth section.

The satellite system considered in this paper is specified as follows (Chobotov, 1991).

In the above, q₀, q₁, q₂, q₃ are the quaternion variables, ω_x, ω_y, ω_z are the angular rates, the matrix I_s includes the elements of the moment of inertia, T_x, T_y, T_z are control input elements, and w_dx, w_dy , w_dz are the external disturbances.

The quaternion vector q that is related to the Euler angle is defined as follows.

In Eq. (2), (I_sω)_x, (I_sω)_y and (I_sω)_z are defined as follows.

The dynamic equations of Eqs. (1) and (2) can be rewritten as follows.

Here, x₁=[q₀ q₁ q₂ q₃]^T, x₂=[ω_x ω_y ω_z]^T,

Note that B = I_3×3 for a healthy condition of the actuator. When one of the actuators partially loses its actuation effectiveness, Eq. (6) can be written as follows:

where the actuation effectiveness matrix, B_f=diag{B_fi},(∀=x~z), is a matrix that represents the fault effect of the actuator. The degradation of the actuation effectiveness in a real situation cannot be clearly modeled. Therefore, the chattering effect with high-frequency variation due to the degradation of the actuation effectiveness also should be considered. In this paper, the effects of the actuator fault, B_fi are modeled as follows.

In Eq. (8), a_fi is the magnitude of the actuation effectiveness, and the second term is the high-frequency variation due to the fault with amplitude b_fi and frequency ω_fi . Usually, the magnitude of b_fi is very small when compared to that of a_fi. For simplicity, let us introduce a matrix, C_f, as follows

The satellite usually performs various maneuvers such as rest-to-rest and despin. In this paper, the rest-to-rest maneuver is considered. The angle of maneuver of the principal axis of the satellite can be represented as follows.

In Eq. (10), f_s(^.) is a smooth approximation of the signum function for the maneuver.

For the rest-to-rest maneuver, the following boundary conditions should be satisfied.

In Eq. (11), θ_f ? θ₀ is the maneuver attitude angle, t_f is the target maneuver time, and T_max is the maximum available torque. In this paper, the following function, f_s(^.), is adopted for near-minimum time control (Junkins and Kim, 1993) to prevent unnecessary activation of the flexible modes of the solar panels.

In Eq. (12), and the torque-shaping parameter, Δt=αt, α, is in the range of 0 <; α≤0.25.

The target maneuver time, t_f , for each axis can be obtained by using Eqs. (10-12) as follows.

Note that each axis's desired reference trajectory for the satellite rest-to-rest maneuver can be obtained by using Eqs. (10, 12, 13).

In this section, a fault tolerant control scheme with a modified iterative learning law is designed to deal with the decrease in the effectiveness of the actuator and the external disturbance.

First, let us design the sliding mode controller to make the satellite attitude angles track the reference trajectory in Eq. (10) using the pseudo control input. Note that the state vector, x₂, in Eq. (5) can be considered as the pseudo control input. This pseudo control input becomes the reference trajectory of the angular rate, x₂.

Using the quaternion vector and the desired trajectory, the sliding surface is defined as:

where the reference trajectory,

, is constructed to perform the rest-to-rest maneuver. Since the condition, q₀²+q₁²+q₂²+q₃²=1, should be satisfied, q₀ can follow q_0d as the sliding surface s approaches zero asymptotically.

Differentiating Eq. (14) with respect to time yields:

where

To satisfy the reaching condition of the sliding surface, the following Lyapunov candidate function is considered.

Differentiating Eq. (16) with respect to time and substituting Eq. (15) into the resulting equation yields:

The pseudo control input vector for the attitude angle can be obtained by the sliding mode control method as:

where K is the control gain matrix, and δ is the boundary layer thickness vector.

The pseudo control input of Eq. (18) is used as the reference trajectory of the angular rate, x_2d.

Substituting Eq. (18) into Eq. (17) gives:

Finally, it is concluded that the stability of the reference trajectory tracking controller is guaranteed.

Now, let us design a fault tolerant control scheme to deal with the decrease in effectiveness of the actuator and the external disturbance. Using the reference angular rate trajectory, x_2d , which is obtained from Eq. (18), and the angular rate state vector, x₂, the angular rate state error vector is defined as:

Differentiating Eq. (20) with respect to time yields:

where T_df(t)=I_s-1[w_d(t)-C_fu(t)] is the influence of the actuator fault and the external disturbance.

Let us select the fault tolerant control input using Eq. (21) as:

where (F_^) is the estimated fault signal that can be obtained using the modified iterative learning law to compensate the influence of the actuator fault and the external disturbance. Usually, faults that occur in the system are unknown. To deal with this problem, the modified iterative learning law is used.

The general iterative learning law is updated by both the previous information and the state estimation error (Chen and Saif, 2001, 2007). Note that the modified iterative learning law proposed in this paper is updated using only the information associated with the state error; therefore, the influence of the actuator fault and the external disturbance can be estimated as follows:

where the parameter, τ, is an updating interval.

The gain matrices, L₁ and L₂ in Eq. (23), are determined using Lyapunov stability analysis. Substituting Eq. (22) into Eq. (21) and using Eq. (23) yield:

Let us consider the following Lyapunov candidate function.

Differentiating Eq. (25) with respect to time and substituting Eq. (24) into the resulting equation yield:

The following inequalities can be obtained (Yan et al., 1998).

The following equation also can be obtained using Eq. (24).

Similarly, the following inequalities can be obtained:

and

As a result, the inequality, Eq. (29), can be obtained using Eqs. (30-32) as follows:

where

and

By assuming

and

, the following can be derived:

where D_max=max(D_x, D_y, D_z) and T_max=max(T_x, T_y, T_z).

By substituting Eqs. (27, 28, 33, 34) into Eq. (26), the following equation can be obtained.

To satisfy Lyapunov stability, the following relation should be satisfied for the gain matrices, L₁ and L₂.

From the above equation, the following inequality is obtained for using the gain matrix, L₂:

where

Therefore, the gain matrix, L₂, should be selected to satisfy the following relation.

In summary, the gain matrices, L₁ and L₂, must be chosen using Eqs. (36, 39), and the fault estimate signal, (수식삽입), of Eq. (23) is updated using the gain matrices and the information associated with the state error.

Remark: The state error can be used for fault monitoring purposes. When there are no faults in the system, the state error should be zero or close to zero. On the other hand, an increase in the state error would point to the occurrence of a fault. After the fault occurs, the estimated fault signal would learn about the fault and the state error will again be driven to zero or a value close to zero. This means that the iterative learning law can learn and update by the previous and the present state error information.

Numerical simulation has been performed to verify the proposed fault tolerant control scheme. The Hubble space telescope is considered as the satellite system (Thienel and Sanner, 2007; Wie et al., 1993). The inertia, I_s, is given as follows.

With regard to the external disturbance, the disturbance that is induced by the solar array is considered as follows (Wie et al., 1993).

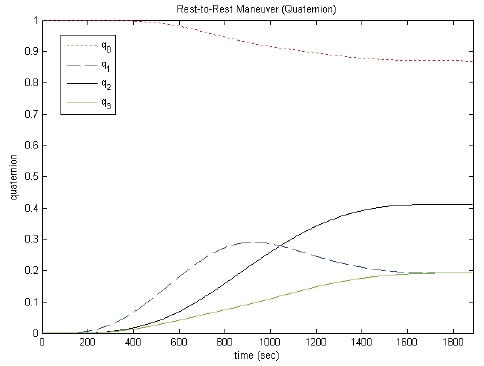
The attitude (quaternion) reference trajectory is for the rest-to-rest maneuver. The maximum value of the available torque, T_max, of the actuator is 0.82 Nm, and the torqueshaping α is selected as 0.25 for a near-minimum smooth maneuver. The initial attitude quaternion is chosen as , the initial reference angular velocity, ω_d(0) is taken as zero, and the initial angular velocity is chosen as (deg/s)(Thienel and Sanner, 2007). The initial and target attitude angles are chosen as 0° and 40°, respectively, about all axes. The target attitude quaternion is calculated as . The final target maneuver time, t_f , which is calculated by Eq. (13), is about 1,886 seconds. This final time is taken as the maximum target maneuver time at each axis. The reference trajectory of the rest-to-rest maneuver with respect to the quaternion values is shown in Fig. 1.

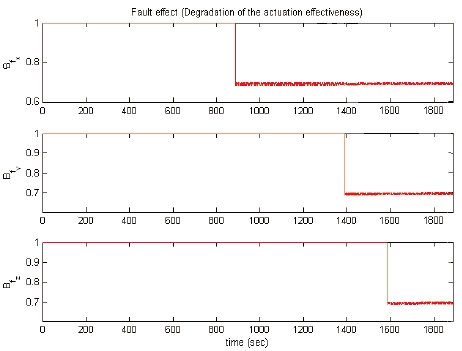
In this case, the actuator faults are considered as follows.

In Eq. (8), the magnitude of the actuation effectiveness with regard to the actuator fault is chosen as 0.7, a_fi = while b_fi and the frequency, ω _fi are chosen as 0.02 a_fi and 5 Hz, respectively. Figure 2 shows the considered change in the fault effectiveness.

The gain matrix is chosen as K=0.1I _3×3, and the updating interval, τ, is chosen as 1 second. The parameters of the modified iterative learning law are chosen as ρ=0.1, γ₁=γ₂=0.1 and γ₃=γ₄=γ₅=10. The upper bound on the external disturbance, D_max, is chosen as 0.4 Nm.

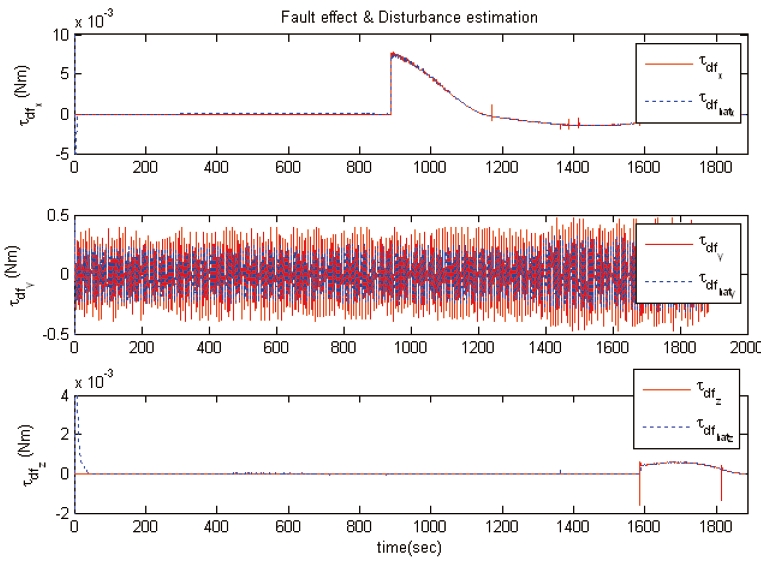
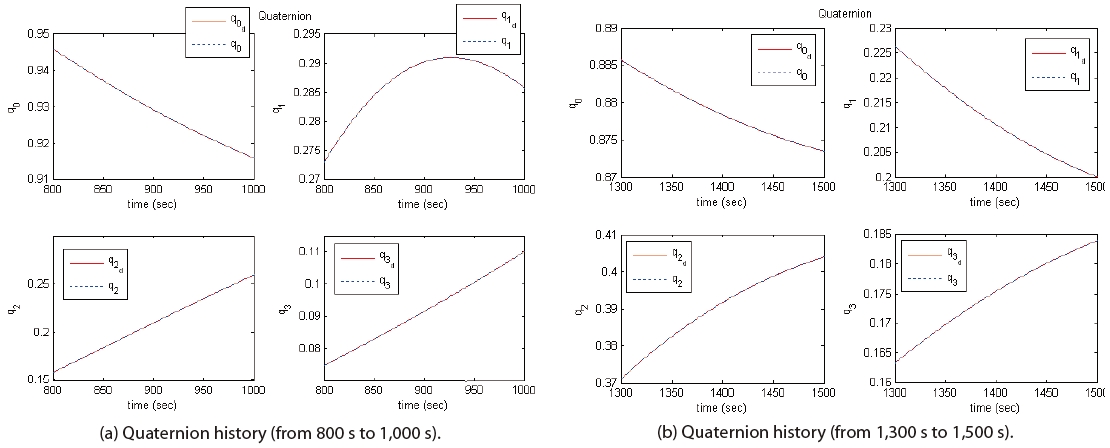
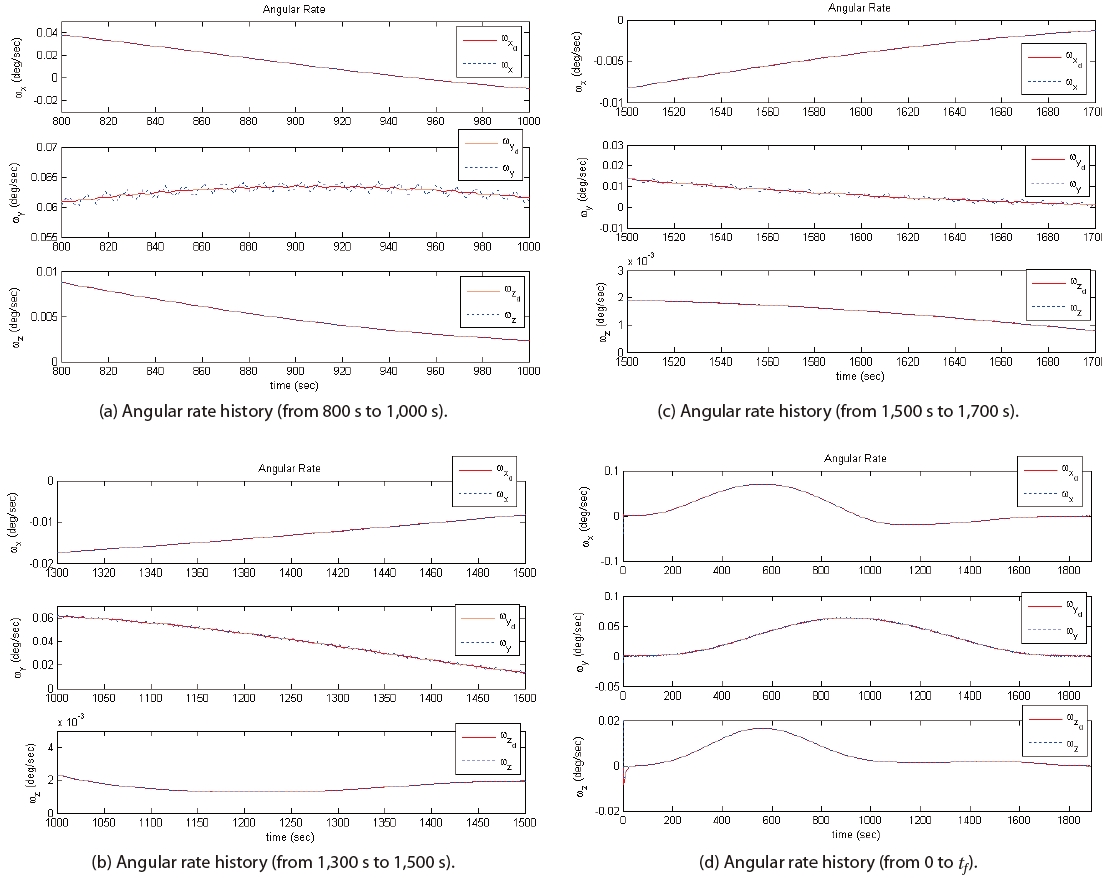
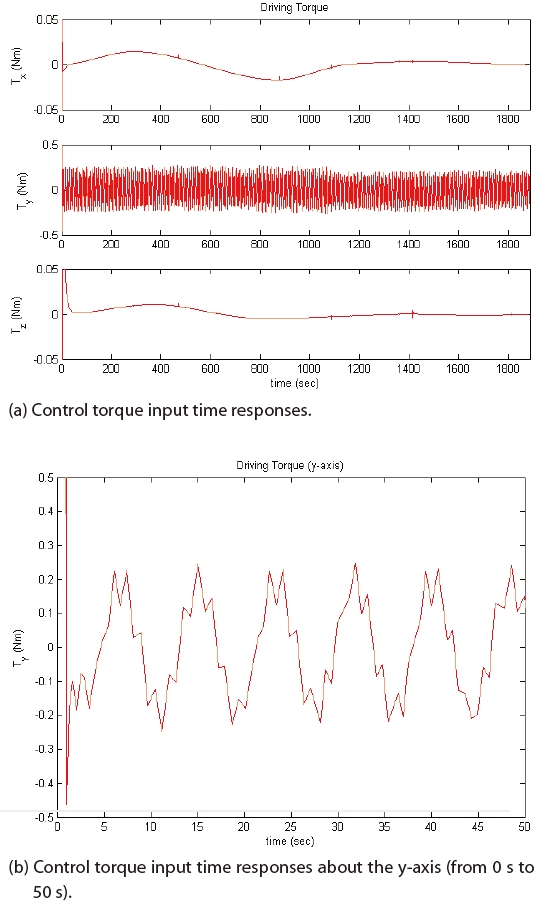
The simulation results are shown in Figs. 3-6. It can be seen from Figs. 3 and 4 that the state values, after the occurrence of the actuator faults, follow the reference trajectories very well. Figure 5 shows that the actuator faults can be estimated by the modified iterative learning law. As shown in Fig. 6, a high-frequency control torque input is used for the y-axis. The control torque input response of the y-axis, from 0 to 50 seconds, is shown in Fig. 6(b); it can be seen that a high-frequency control input is required to deal with the disturbance that is induced by the solar array. As seen in the simulation results, the fault tolerant control scheme with the modified iterative learning law deals with the actuator faults and the external disturbance.

In the second case, numerical simulation is performed for actuator faults that occur at same time. The actuator faults are considered to occur at t = t_f- 800 sec about all axes. All the design parameters are identical to those in Case 1. Figure 7 shows the considered change in the fault effectiveness. The simulation results are shown in Figs. 8-11. It can also be seen that the proposed fault tolerant control scheme with the modified iterative learning law copes well with the simultaneous occurrence of actuator faults.

A satellite attitude control scheme is proposed to deal with actuator faults and external disturbances. The reference attitude angle of the satellite is designed using a near minimum-time maneuver in the rest-to-rest maneuver. A fault tolerant control scheme for the satellite attitude system with a modified iterative learning law is proposed to deal with the degradation of the actuation effectiveness and the external disturbance due to the vibration of the solar array. The modified iterative learning law is considered to estimate the unknown influence of the actuator fault and the external disturbance. Note that only information that is related to the state error is used. The fault tolerant control scheme is applied to a large satellite system, and the performance of the proposed satellite attitude control scheme is verified by numerical simulation. The proposed algorithm can be applied in an attitude control system to improve the reliability of satellite systems.