A typical aircraft design consists of conceptual research, conceptual design, preliminary design, and detailed design processes. In the conceptual design process of an aircraft, data from comparisons and analysis of the current aircraft are used as the presumptive data for the aircraft's configuration and performance, and the conceptual configuration of the aircraft is derived by repetitive designing processes. Final design configuration is selected after analyzing and examining the degrees of satisfaction, technical possibility, and price for the design requirements of such derived configurations (Jung et al., 2004; Lee and Park, 1996; Won et al., 2008).

For the multi-rotor type rotorcrafts, it is possible to derive a design that satisfies mission requirements in the conceptual design stage by applying the method mentioned above. However, aircraft design generally carries a difficulty of deriving a new configuration, which appears to be clearly distinct from a conventional aircraft since the design is highly affected by the factors such as current aircraft configurations, domestic and foreign design cases, and designer's individual preferences.

Therefore, in order to derive a new conceptual configuration, a new method referred to as the Axiomatic design method has been applied in the preliminary conceptual design process stage of a multi-rotor unmanned aerial vehicle (UAV). Until today, the axiomatic design method has been successfully applied to the conceptual design process, which requires a creative design. Furthermore, the axiomatic design could be applied to new aircraft creations through fundamental processing methods of an aircraft.

The axiomatic design has been developed in order to merge the standardized design theory with objective and universal principles. More specifically, axiomatic design can be referred to as a design framework, which contains the principles applied to a typical engineering process (Park and Kang, 2005).

In an axiomatic design framework, a good design is considered as one that satisfies both the following two axioms: independent axioms and information axioms. If the two axioms are not satisfied, a design is not considered a good design. In this study, the word "axiom" will possess the same definition as that used in geometry: an unproven idea becomes a false idea if at least one counter example exists. So far, there is no counter example found on any of axiomatic design cases, so the applications of the axiomatic design on the aircraft design cases is a valid methodology for the improvement of aircraft performances (Seong et al., 2001).

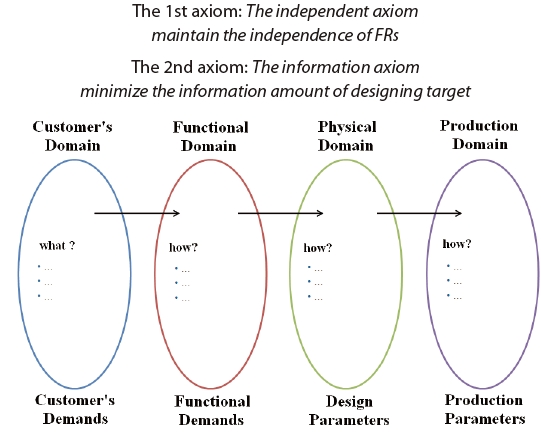
During the design process stage, four domains of the design sequence are carried out, as represented in Fig. 1. In a customer's domain, customer demands are defined in a descriptive manner; and, these demands are known as the customer attributes (CAs). Defined facts from the customer's domain are converted into functional requirements (FRs) in the functional domain. FRs are redefined as customer's requirements of the customer's domain in engineering terms. Functional demands are satisfied by defining and appointing design parameters (DPs) in the physical domain. Usually, this whole process is called as the design process. After appointing DPs, production variables for the production are to be defined. In the same manner, after the design process in the axiomatic design understands the relationship between the two domains, then it decides the event in the next domain via defined facts in previous domain. This process is called 'events among domains.'

Axiomatic design is an intensive expression of common principles that works for every engineering behavior , and it is defined by following two axioms (Won et al., 2009).

The principle of the independent axiom is that a good design independently satisfies events of the left hand side domains with defined events on the right hand side domains in Fig. 1. When multiple FRs are defined, each DP should be able to satisfy each FD independently. By utilizing the design matrix A, such FR-DP relationships can be represented as the following equation.

The characteristics of matrix A decide whether or not the Independent axiom has been satisfied. For the case of the FR vector and the DP vector each having three elements, the matrix A can be represented as follow.

Here, it is called as an uncoupled design for the case of A being a diagonal matrix. Additionally, each DP is able to satisfy the corresponding FR independently, subsequently satisfying the independent axiom. For the case in which the design matrix A is a triangular matrix, which is referred to as a decoupled design case, it is possible to satisfy the FR independently according to the sequence determining the DP. For the case in which the design matrix A has non-zero diagonal terms, FR and DP have a coupled relationship in any sequence, and it is called the coupled design. Uncoupled or decoupled designs are considered 'satisfactory' for the independent axiom, and a coupled design is regarded as a 'violation' of the independent axiom.

In an axiomatic design, the independent axiom should be satisfied first. However, as it is possible for deriving multiple aircraft design plans satisfying the same demanding requirements, it is also possible to find more than two designs satisfying the independent axiom. For this case, in order to select the best design out of the possible designs, the design with the least amount of information satisfying the information axiom is the one to be selected. A greater amount of information implies greater complexity of the model. Calculating the amount of information in the information axiom requires the application of an index number. The index number may possess different definitions for each design's characteristics; however, the most applicable index for general designs is known as the probability of success. The variable p signifies the probability of success for a specified DPi satisfying its FRi; consequently, the amount of information Ii could be defined as follows.

In this expression, the inverse of the probability is taken to minimize the amount of information as the probability increases; and, the logarithmic function is used to increase the additive ability of the information amount. However, closer attention should be paid to the fact that the information amount can only be defined by the FRs.

In the preliminary conceptual design process of tri-rotor rotorcraft, the axiomatic design could be applied to derive a creative configuration. In order to apply the axiomatic design, customer's demands, functional demands, DPs, and constraint conditions should be defined in each domain of the whole design process. These are listed in Table 1. The CAs are not considered in order to concentrate on creative design and its evaluation. The list in Table 1 can be modified by designer's experience and specific design requirements.

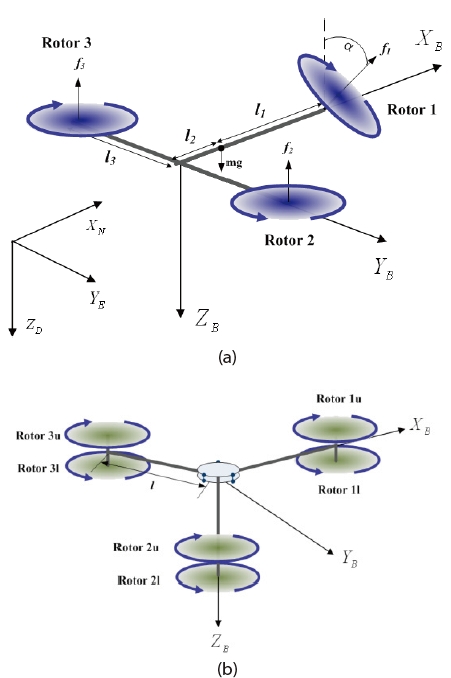
In the following example, the axiomatic design has been applied to a tri-rotor rotorcraft design to offer a creative possibility, and three configuration concepts have been analyzed in design axiom manner. Based on each design domain definition listed in Table 1, FR vectors, which are applied to each configuration equally, are defined in Eq. (4). By listing the DP vectors for three configurations of tri-rotor rotorcraft, it is possible to check whether or not it satisfies the independent axiom. In this case, constraints are thought of as the configuration with three rotors that satisfy the constraints in Table 1. The numerical values in parentheses of the DP vectors represent the defined probability of success for the functional demand.

Definition of FRs vector

Design example 1

Design example 2

Design example 3

Because each DP in design examples 2 and 3 satisfy the FRs independently, they could be considered as appropriate 'satisfactions' of the independent axiom. However, design example 1 does not satisfy the independent axiom because the first and fifth DPs are identical. Thus, even if design examples 1 and 2 provide the same configurations, the first one can be canceled outby its control strategies. Conclusions drawn from the design examples are that the derivations of multiple configurations satisfying identical FRs are possible; and, for any design configuration it is possible to determine whether or not it satisfies the design axiom with analysis of FRs and DPs, which are defined in design domain.

Furthermore, in the preliminary design process, the information axiom could be applied to the case of selecting one final configuration out of the multiple derivations of configurations. In the information axiom applications, the final configuration design plan can be decided upon by selecting one with the least information amount in each design after comparisons. For design examples 2 and 3, the total information amount from the probability of success in the DPs could be calculated as follows. In Eqs. (8) and (9), pi is the DP from Eqs. (5-7).

Hence, for the preliminary conceptual design of trirotor type rotorcraft it is possible to derive two different configuration designs and finally be able to select the configuration design plan of design example 3 by applying the axiomatic designing method. In the process of calculating the information amount, probability of success for each DP can directly influence the information amount. It can also assign more or less weight depending on the level of its gravity, which could also depend on the designer's subjective decision.

As another example, the quad-rotor UAV, the multi-rotor UAV with four rotors, has been considered. FRs, DPs, and constraints of quad-rotor are identical to those of tri-rotor UAV, which is listed in Table 1. In Fig. 3, there are three types of quad-rotors introduced for comparison. FR vectors are the same as those of tri-rotor UAV, as shown in Eq. (4). Based on the designs of the quad-rotor UAVs in Fig. 3, the numbers for each DP can be calculated. The DPs for the quad-rotor examples 1 to 3 are listed in Eqs. (10-12).

In the same manner as previously discussed, by analysing Eqs. (10-12), it is possible to derive the total information amount from the success probability of the DPs. Eqs. (13-15) give the total information of each quad-rotor design; recall that the same equations were used for the tri-rotor UAVs.

Among the three designs of quad-rotor UAVs, the axiomatic design indicates that the example 1 is the best choice for the quad-rotor UAV.

In this paper, the axiomatic design method was applied to the preliminary conceptual design of multi-rotor UAVs in order to derive new configurations. Generally, the process of designing an aircraft is affected by domestic and foreign design cases, as well as the designer's subjective preferences. The various influences affecting the design process of an aircraft leads to the research, discovery and analyses of various aircraft configurations. These results may be acquired from a systematic design method such as the Axiomatic Design. Although the axiomatic design offers a systematic engineering design and evaluation method using a design framework, the experience of aircraft designers or technology will still occupy a major part in the process when deciding the functional demands, the DPs, and the probability of success.