Recently, Surface Plasmon Polaritons (SPPs) have gained much attention due to their ability to confine light at a subwavelength scale [1]. SPPs are electromagnetic waves coupled to free electrons in metal. They propagate tightly bound to interfaces between a dielectric and a metal [2]. Optical waveguides based on SPPs have been extensively studied as modulators [3], filters [4,5], optical attenuators[6], and switches [7]. Among a variety of SPP waveguides proposed to date, the Insulator-Metal-Insulator (IMI) [8,9] or the Metal-Insulator-Metal (MIM) [10,11] have been the most widely investigated and have become the most fundamental building blocks of nano-photonic integrated circuits. The IMI SPP waveguide exhibits very low loss propagation with poor localization on the order of several micrometers and it is not suitable for high-density photonic integration. Conversely, the MIM structure can confine light beyond the diffraction limit, allowing rendering of highly integrated optical devices. Its propagation length, however, is extremely short compared to the IMI and to any other conventional dielectric waveguides [11]. Thus there is a tradeoff between good confinement and long propagation length. In order to overcome this problem, Dielectric-Loaded SPP Waveguides (DL _SPPWs) [12,13] and a symmetric DL _SPPW (SDL _SPPW) [14] have been proposed and comprehensively analyzed, but the optimal design method has not been presented to date.

On the other hand, Genetic Algorithms (GAs) have been employed for optimal design of optical devices such as optical filters [15,16], long-period fiber gratings [17], and waveguides [18]

In this paper, we propose the use of a Genetic Algorithm (GA) to optimize mode confinement and propagation length of a DL _SPP waveguide at a telecom wavelength (1550 nm). First, we investigate the effects of variations in the thickness, width and refractive index of the dielectric ridge on mode confinement and propagation length. The Effective Index Method (EIM) [19] was employed to obtain the optical properties of the DL _SPPW. The design results show that a DL _SPPW mode with high confinement and relatively low loss is realizable.

A schematic diagram of the DL _SPPW is shown in the inset of Fig. 1 (a). The structure consists of a polymer ridge with thickness t and width w on top of a gold film of thickness d. The gold film is on top of a substrate. In the calculations hereafter, the reference parameters are as follows: the refractive indexes of the polymer, substrate, gold and air are 1.65, 1.46 [14], 0.5590 + 9.8100i [20] and 1, respectively. The metal thickness d =100 nm, and the excitation wavelength is 1550 nm. We use these values if not mentioned otherwise.

The electric field can be expressed in the form:

where β is the complex propagation constant β=β'-iβ'', which is related to the mode effective index according to β'=k₀n_eff and the propagation length is defined as L_sp=1/(2 β'') with propagation constant k₀ in a vacuum.

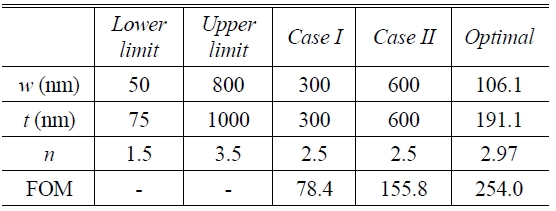
In Fig. 1 (a), we show the effective index n _eff and propagation length L _sp of the fundamental DL _SPPW mode as a function of the ridge width w for different ridge thicknesses. It is clear that as w increases, n _eff increases and L _sp decreases, which corresponds well with the general characteristics of general dielectric waveguides. Increasing the ridge width produces a high electric field along the interface between the polymer and metal, and thus, the fraction of power density in the metal rises, implying a higher propagation loss and a corresponding decrease of propagation length. Similarly, it is also shown that increasing thickness t causes higher n _eff and shorter L _sp.

In general, there is a tradeoff between the mode confinement and propagation length of the SPP modes. For a metric to evaluate waveguide performance including both parameters, we define the Figure of Merit (FOM) as (수식처리) where M_s is the area in which the power density is more than 1/e² times its maximum value.

In Fig. 1 (b), we show the FOM as a function of the ridge width w for different ridge thicknesses. All other parameters are the same as those in our reference structure. It can be seen that the FOM is not monotonic with respect to the ridge width w but exhibits a maximum around 100-200 nm. It should also be noted that as t increases, the FOM increases, due to the fact that as t increases, L_sp increases sharply but M_s does not change significantly.

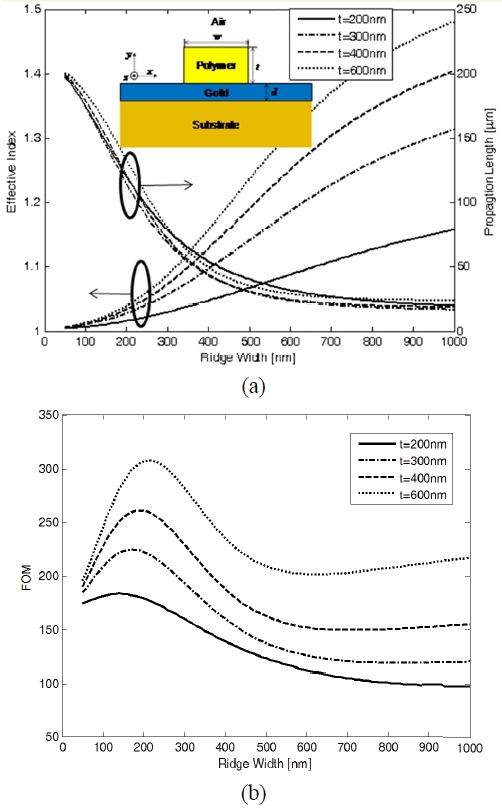
In Fig. 2 (a) we show the effective index n _eff and propagation length L _sp of the fundamental DL _SPPW mode as a function of the ridge thickness t for different ridge widths. It is clear that for very thin film thickness, the values of n _eff and L _sp approach those of SPP propagating along a gold-air interface in all cases: n _eff →1.0052, and L _sp →206.4 μm. It is apparent from the figure that the effective index increases monotonically with respect to both the ridge width and thickness. Decreasing the film thickness, however, raises the fraction of power density in both the polymer and the metal due to the squeezing effect [12], and therefore reduces the propagation length. The propagation length decreases with decreasing polymer thickness until it reaches some point at which it exhibits a minimum. Beyond the thickness, length L _sp increases rapidly with decreasing polymer thickness.

In Fig. 2 (b) we show the FOM as a function of the ridge thickness t for different ridge widths. We observe that the FOM is not monotonic with respect to the ridge thickness t but exhibits a minimum around 100-200 nm. It is noteworthy to mention that as w increases, the FOM increases.

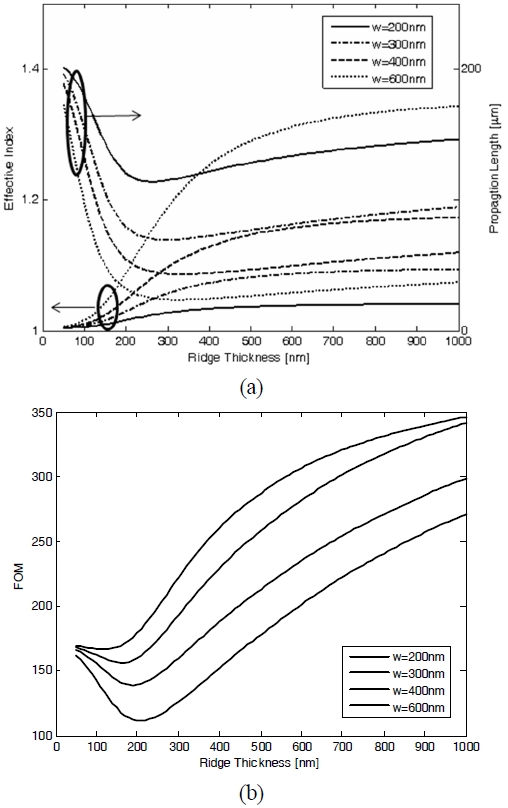
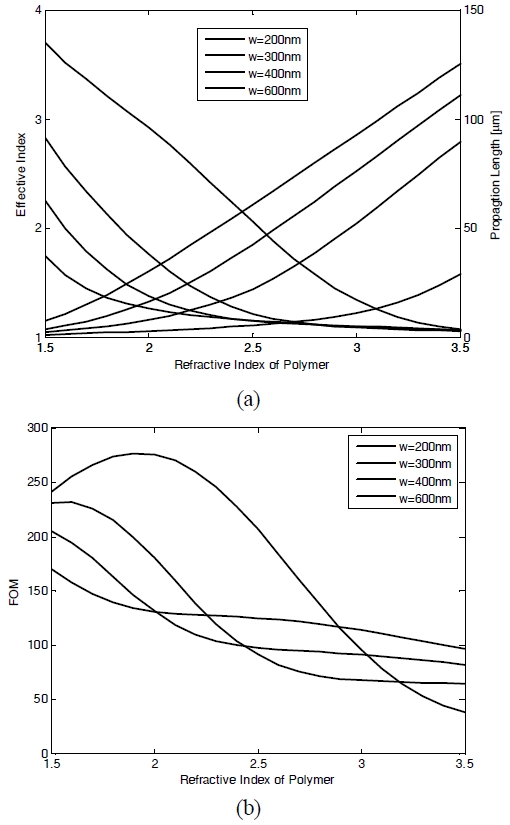
Furthermore, n _eff and L _sp are dependent on the refractive index of the ridge polymer. In Fig. 3 (a) we show the n _eff and L _sp values of the fundamental DL _SPPW mode as a function of the refractive index n for different ridge thicknesses. Both n _eff and L _sp exhibit monotonic variation with respect to the refractive index n . FOM also decreases monotonically with n unlike the cases of ridge width and thickness variation (as shown in Fig. 3 (b)).

In Fig. 4 (a) we show the n _eff and L _sp values of the fundamental DL _SPPW mode as a function of the refractive index n of the ridge polymer for different ridge widths. It is apparent that n _eff increases and L _sp decreases with respect to the refractive index n . From Fig. 4(b) it can be seen that the FOM, however, does not exhibit monotonic variation with respect to n, unlike the cases of different ridge thicknesses (as shown in Fig. 3 (b)).

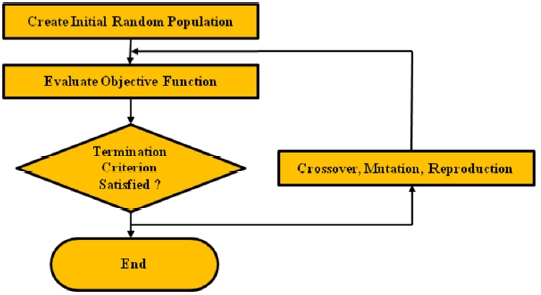
The Genetic Algorithm (GA) is a powerful and efficient method for optimization problems of a given function. The basic theory of the GA was first proposed by John Holland in 1975 [21], and further developed by Goldberg [22]. It is based on a stochastic technique, and a population of individuals is created randomly at each generation. The GA emulates natural evolution selection and survival of the fittest. At each step, it modifies a population of individual solutions and creates a new generation based on the three operators of selection, crossover and mutation. Figure 5 shows the flow chart for designing an optimal DL _SPPW for a FOM, which is expressed as an objective function in the chart and is also called a fitness function in optimization theories.

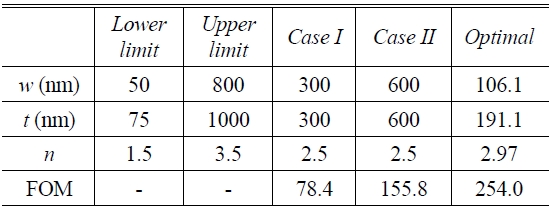
GA optimization is applied to the thickness t , width w , and refractive index n of the ridge in order to design a DL _SPPW with high mode confinement and low propagation loss. All other parameters are the same as those in our reference structure. Here we define the objective function as the FOM defined earlier. In this form of GA optimization, the search ranges of the thickness, width and refractive index of the ridge (t, w, n ) are chosen as [50 800] (nm), [75 1000] (nm), and [1.5 3.5], respectively. The mode profile of the DL _SPPW is not symmetric [12], and the lateral extent is wider than the vertical one at the same width and thickness of the ridge. Since increasing the thickness renders the lateral extent shorter, we apply the following additional constraint to our problem for coupling with other optical waveguides having a symmetric mode:

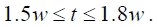
Furthermore, Figs. 2(b) and 3(b) show that a larger thickness is advantageous for our FOM. However since such waveguides operate in multimode fashion, we apply a constraint of single-mode operation to our optimization problem.

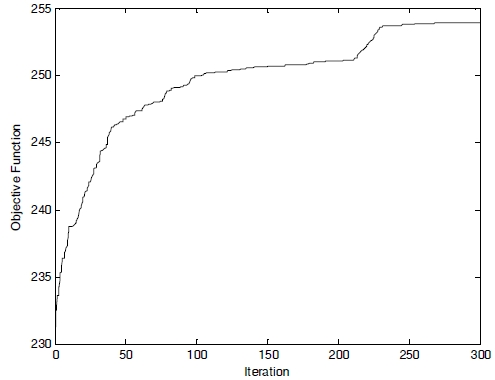
In our computations, the following parameters were used: the population size was 100, the crossover rate was 0.8, and hence the mutation rate was 0.2. The number of generations was fixed at 300 runs. In the attempt to obtain the optimal design parameters satisfying the constraints, we implemented the GA with the above setting parameters. The optimal parameters obtained were t=191.0 nm, w= 106.1 nm, n=2.97. In Fig. 6, we show the optimization results with respect to the number of generations, where it can be seen that the FOMs increase and converge to the optimal value of 254.0 as the number of generations increases. The objective function corresponding to the best design at each generation will converge faster if the population size is larger, which is consistent with general expectations. It was also found that the maximum number of generations, 300, is sufficient for our form of optimization. The optimum design results are summarized in Table 1. When compared with the previous results [12], the FOM value was improved by a factor of 3.2 (300×300 nm2: 79.375) and 1.6 (600×600 nm²:158.75)

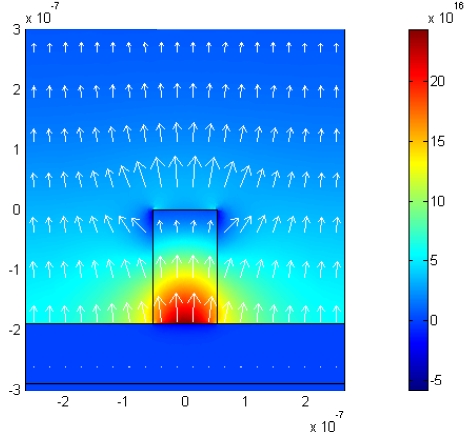
Fig. 7 shows the electric field distribution (arrows) and power density (colored surface) for the DL _SPPW with this optimal FOM. From the figure, it can be seen that the final DL _SPPW confines the light within the ridge successfully while ensuring low-loss propagation. The numerical results also show that the mode profile is nearly square and the dimensions are small enough to implement singlemode operation as a result of introducing our mode shape and single-mode operation constraints.

This paper presents an efficient and powerful approach to optimization of the DL _SPPW for mode confinement and propagation loss. The thickness, width and refractive index of the ridge have been optimized to achieve well-confined light propagation with low propagation loss. The EIM has been employed to analyze the DL _SPPW and obtain the optical parameters. In order to optimize the FOM including mode size and propagation length, the GA has been used. The FOM is as large as 254.0 with the optimal design variables, which is improved by a factor 3.2 and 1.6, respectively when compared with the results previously reported. It is also possible to develop a similar optical waveguide with subwavelength confinement based on SPP using the optimization scheme proposed here.