Random fluctuations of fiber birefringences cause polarization- mode dispersion (PMD) effects detrimental to high bit-rate channels. The PMD effects can be described using a PMD vector whose magnitude is equal to the differential group delay between two principal states [1], [2]. When there are many optical channels or the channel bit rate is high, the angular frequency derivative of the PMD vector becomes also important [3]. Often, the conventional PMD vector is called the first-order PMD vector while its angular frequency derivative is called the second-order PMD vector.

In [4], Foschini and Shepp derived a joint characteristic function for two white Gaussian vector processes in a compact functional form using a sine-cosine Fourier expansion representation. The joint characteristic function is a Fourier transform of the joint probability density function (pdf) of two vector processes. Shortly after [4], it was shown that, when the fiber transmission distance is large, the joint characteristic function can be used for the first- and second-order PMD vectors in highly birefringent fibers [5]. This joint characteristic function has been used extensively to describe various distribution characteristics of PMD vectors [6-8]. The birefringence vector model used in [5] assumes a fixed linear birefringence with much smaller linear and circular random birefringences in equal amounts. Interestingly, the joint characteristic function of [5] agrees with the result of [9] that uses the model of [5] without the fixed linear birefringence component. However, installed optical fibers are almost linearly birefringent [10]. Thus it is worthwhile to justify the joint characteristic function of [5] for installed fibers.

Regarding the birefringence components as white Gaussian processes, a Fokker-Planck equation [11] was derived in [12] to investigate the pdf behavior of the first-order PMD vector in linearly birefringent fibers. The Fokker-Planck method was used also in [13] to find a more correct joint characteristic function for the birefringence vector model of [9]. The second-order angular frequency derivative of the fiber birefringence vector was included in [13] but was neglected in [5] and [9]. The birefringence vector distribution of [9] and [13], having linear and circular random birefringences in equal amounts, has a spherical symmetry in Poincare space. This symmetry helps to find the joint characteristic functions of [9] and [13]that are dependent only on the magnitude of two PMD vectors and the angle in between in their Fourier domain. However, the spherical symmetry does not hold for installed optical fibers and, to our knowledge, the joint characteristic function for installed optical fibers is still unknown.

In this paper, we find the joint characteristic function for installed optical fibers. We use the Fokker-Planck method and include the second-order angular frequency derivative of the fiber birefringence vector. Our final result obtained after a complicated procedure has a compact functional form similar to the previous joint characteristic functions [5, 9, 13].

At first, we will present details of the Fokker-Planck method of [12] along with a new shortcut procedure for finding the pdf of the first-order PMD vector. Then we extend the approach to find a Fokker-Planck equation (in Fourier domain) for the first- and second-order PMD vectors. The asymptotic solution of our Fokker-Planck equation yields the joint characteristic function.

The dynamical PMD equation,

describes the evolution of the first-order PMD vector, τ =(τ 1, τ 2, τ 3) along the fiber [1]. L is the fiber transmission distance. β is the birefringence vector and βΩ=∂β /∂Ω, where Ω is the angular frequency. For linearly birefringent fibers, we set

where

is a zero-mean white Gaussian process having a correlation property,

denotes the ensemble average and δij is the Kronecker delta. This modeling neglects the spatial size of the correlation length compared with the large parameter L [9], [12], [13]. The proportionality factor a is a function of Ω and we will denote da/dΩ as aΩ. Similarly, dβ/dΩ is simplified to βΩ=aΩ

etc.

We note that the vector equation (1) is composed of three Langevin equations,

where N(=3) is the number of variables. The matrix formed by g_ij is

Then we find the Fokker-Planck equation as follows [11]:

where D_i and D_ij are drift and diffusion coefficients, respectively, defined as

From these relations, we have D₁=-a²τ₁, D₂ =-a²τ₂, D₃=-a²τ ₃, and

P=P(τ, L) is the pdf for τ . Since the input signal has experienced no PMD degradations, the initial condition is a Dirac delta function, P(τ ,0) =δ (τ).

The Fokker- Planck equation for the first-order PMD vector is given by

where

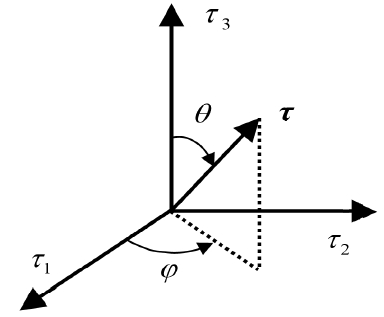
As is shown in Fig. 1, we use a spherical coordinate using the following transform relations [14]:

The positive τ 3-axis is the polar axis. θ and φ are polar and azimuth angles, respectively. Since our problem is invariant to the rotation about the τ 3-axis, we may set ∂/∂φ=0. Then the differential operator K can be simplified greatly as

This equation implies that (5) is a diffusion equation along τ 1, τ 2, and θ directions. Therefore, in the asymptotic region, where the transmission distance L is large, P=P(τ , L) becomes smooth and widely spread in τ space.

We expand P(τ , L) in terms of Legendre polynomials as

The n-th order Legendre polynomial, P_n(cosθ), is an eigenmode of the a² term such that

Since P_n(cosθ) is not the eigenmode of a_ω² terms of (10), there are couplings between these modes during the transient region. The initial condition, P(τ , 0)=δ(τ ), belongs to the P₀(cosθ) mode and A_n(τ , 0) for n≠0. As L increases from zero, the magnitude of A_n(τ , L) (n≠0) increases owing to the coupling with the n=0 mode. Actually, these couplings exist only between even- modes owing to the even symmetry of our problem with respect to the θ coordinate. Note that the a² term in (10) is dependent only on the angular variable θ while the a_ω² terms are not. Thus, in the asymptotic region, where P=P(τ , L) becomes smooth, the a² term becomes dominant compared with the a_ω² terms for n≠0 modes. If a_ω² terms are neglected, A_n(τ , L) decays in proportion to exp{-n(n+1)a²L}. It implies that, in the asymptotic region, we have P(τ , L)=A₀(τ , L) ultimately. This can be verified also using a multiple-scale method [15].

To find A₀(τ , L) in the asymptotic region, we set ？/？θ= ？/？φ=0 for the spherical coordinate representations of ？²/？ τ ₁ ² and ？²/？τ ₂ ² terms in K, which gives

Next, we remove the terms in K that couple A₀(τ ) with other A_n(τ , L) (n≠0) components. This can be achieved by applying (1/ 2)f^π₀ d θ sin θon K, which leaves only the P₀(cosθ) component in K. The result is

Thus, in the asymptotic region, P(τ , L) becomes a Gaussian, exp

with a variance σ²(L)=4a_ω²L/3. This also implies that the magnitude of the first order PMD vector's pdf converges to a Maxwellian [2].

We have used the same initial condition, P(τ, 0)=δ(τ), to solve (13). This can be verified by taking a Laplace transform of (5) to find

where

is the Laplace transform of

with respect to L. The initial condition term, δ(τ), also belongs to the P₀(cosθ) mode and remains the same in the asymptotic region. Thus the initial condition, P(τ, 0)=δ(τ), can be used for (13).

From (1), we find a differential equation for the secondorder PMD vector, τω=？τ/？ω=(τ_ωl, τ_ω2, τ_ω3), as follows:

where β_ωω=？²β /？ω²=a_ωω(γ₁, γ₁, 0). We note that (1) and (14) can be regarded as six Langevin equations, ？ ？ =

where N=6. x_i=τi for i = 1, 2, 3 and x_i=τ_ωi for i = 4, 5, 6. Now g_ij set forms a 6×6 matrix that will be used to find new drift and diffusion coefficients in the Fokker-Planck equation, (3). Its solution is the joint pdf of τ and τ_ω which will be denoted as P=P(τ, τ_ω, L).

We will solve the Fokker-Planck equation in the Fourier domain by introducing a joint characteristic function,

where k=(k₁, k₂, k₃) and k_ω=(k_ω1, k_ω2, k_ω3). Our definition of the join]t characteristic function is the complex conjugate of the conventional one. The differential equation for the joint characteristic function is given as

where the differential operator M is given by

In (18), we have introduced angular momentum operators defined as L_k =-jk ×∇_k = (L_k1, L_k2, L_k3), L_kω= -jk ×∇_kω=(L_kω1, L_{kω 2}, L_{kω 3}), and L_tot=L_k+L_kω=(L_tot1, L_tot2, L_tot3) [16]. ∇_k and ∇_kω are del operators in k and k_ω domains, respectively. L_tot=L_tot1+L_tot2 and L_tot-=L_tot1-L_tot2 are raising and lowering operators, respectively, for the total angular momentum operator, L_tot. Since the input signal has experienced no PMD degradations, the initial condition is Q(k, k_ω, 0) = 1 or P(τ ,τ_ω, 0)=δ(τ)δ(τ_ω).

As is shown in the Appendix A, we can find E{τ²}=4a²_ωL from (16) using the relation, E{τ²}=-∇²_kQ(k, k_ω, L)'_k=kω=0 . In a similar way, E{τ²_ω} is found as 16a⁴_ωL² /3+4a² _ωωL(1-a⁴_ω /9a² _ωωa²)+2a ⁴_ω {1-exp (-6a²L )}/ 27a⁴. As L becomes large, the ratio E{τ²_ω}/(E{τ²})² converges to 1/3 [5]. In this asymptotic region, Q(k, k_ω, L) becomes localized to the origin k=k_ω=0.

Since E{τ²_ω} >>E{τ²}, Q(k, k, L) shrinks faster in k_ω domain than in k domain as L increases.

The L² _tot operator has eigenvalue L_tot(L_tot +1), where L_tot is a non-negative integer. We may expand Q(k, k_ω, L) using the eigenmodes of L²_tot. The L²_tot operator is composed of angular variables only and becomes dominant in the asymptotic region. The other terms in M become less effective. This is because, as is mentioned above, Q(k, k_ω, L) shrinks to the origin k=k_ω=0 and the shrink speed is faster in k_ω domain. Thus eigenmodes with L_tot ≠ 0 become negligible in the asymptotic region and only the eigenmode with L_tot = 0 survives. Note that this procedure is similar to the foregoing first-order PMD vector analysis. The L_tot = 0 condition also implies that the only possible eigenvalue of L_tot3 is zero since -L_tot≤ L_tot3 ≤L_tot. Thus we have L_tot±Q =L_tot3Q = 0 or

From (24), we find kLQ_kω =k_ωL_k Q = 0. Using these relations, it can be shown that D and F terms in the operator M disappear, i.e., DQ = FQ = 0 . As a result, there are no differential terms for k_ω in the operator M and k_ω becomes just a parameter in the asymptotic region. The symmetry in (24) implies that the asymptotic solution should be dependent only on the magnitudes of k and k_ω vectors and the angle in between. This can be proved simply by rotating the coordinate such that one of k or k_ω vector becomes a polar axis.

To find the asymptotic solution satisfying this condition, let's assume that the k_ω vector is located in the k vector domain as is shown in Fig. 2. Since our problem is invariant under the rotation about the k₃-axis, we have set k_ω2. We rotate the (k₁, k₂, k₃) coordinate about the k₂ -axis into the (k₁', k₂', k₃') coordinate, where the k₃' -axis coincides with the k_ω vector's direction.

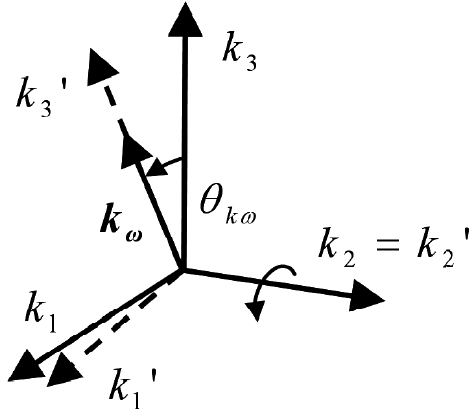
The corresponding rotation matrix is

where θ_ωk is the polar angle of k_ω before the rotation. With (25), we apply the transform relations

and

to M, where R_ji is the matrix element of the inverse rotation matrix R(-θ_kω). Then the remaining operators, B, C, and E, are transformed into

In the transformed (k₁', k₂', k₃') coordinate, the asymptotic solution is not dependent on the azimuth angle φ′. Thus we set ？/？φ'=k₁'？/k₂'-k₂'？/？k₁=0 in M. In addition, we apply

on M to remove θ_kω and φ′ dependences in M. This operation removes the couplings between the -L_tot = 0 mode and the other modes with -L_tot ≠ 0. Then cos² θ_ωk, sin² θ_ωk, and cosθ_ωksinθ_ωk, factors become 1/3, 2/3, and 0, respectively. Also, cos²φ', sin²φ', and cosφ'sinφ' factors become 1/2, 1/2, and 0, respectively. Besides, we find ？/？k₁'² = ？/？k₂'².

Finally, we obtain the following differential equation for the asymptotic solution:

where we have omitted the prime notation. As before, the initial condition remains the same, Q(k, k_ω, 0) = 1. We decompose Q(k, k_ω, L) as

where q satisfies

Equation (31) can be solved using the separation-of-variables method as

where H_2m(^.) is the Hermite polynomial. Using an expansion formula for a Gaussian function,

we find

Thus, for an arbitrary direction of k_ω, the joint characteristic function becomes

where σ² =E{τ₁²}=E{τ₂²}=E{τ₃²}=4a²_ωL/3 as in the previous section. k_// is the component of k parallel to k_ω and k²₁=k^2-k²_//.

In the limit of large L, the cosh (k_ωσ²) term in (35) implies that the effective range of k_ω decreases as O(L^-1) since σ² ∝L. Also, the exponential terms in (35) imply that the effective range of k_i(i=1, 2, 3) decreases as O(L-^1/2). Thus we may neglect the a_ωω term in (35) as L increases indefinitely. In this limit, (35) becomes the same as the joint characteristic function of [5] with reevaluated appropriate to the linearly birefringent fiber. This feature also holds when the fiber has both linear and circular birefringences in equal amounts [9], [13]. The a_ωω term can be meaningful for practical transmission distances. For example, the second-order PMD vector components can be Gaussian-like distributed instead of a soliton shape [2]. This point has been shown in [13] and presented in Appendix B.

With the

condition, the first-order PMD vector distribution has an azimuthal symmetry for all L in [12]. However, the azimuthal symmetry is not evident in our analysis of joint-characteristic function where the number of variables is doubled from 3 to 6. In fact, our final asymptotic solution (35) has spherical symmetry. The coordinate orientation does not affect our result. This kind of spherical symmetry for the asymptotic joint-characteristic function is also found in [5], [9], and [13].

It is also interesting that (35) is quite similar to the result of [13]. The only difference is the change of L into 2L/3 in our case. In [13], the birefringence vector was assumed as

is also a zero-mean white Gaussian process having a correlation property,

Note that the number of random birefringence components is larger than our case. Thus, for given a, a_ω, and a_ωω values, the joint characteristic function reaches to its asymptotic form faster than our case as the transmission distance increases. In this respect, the scaling factor 2/3 can be regarded as the ratio of the birefringence component numbers.

We have found a joint characteristic function for the first- and second-order PMD vectors in installed fibers. As the fiber transmission distance increases indefinitely, our joint characteristic function resembles that of [5] obtained for highly birefringent fibers. This agreement may not hold for practical transmission distances owing to the secondorder angular frequency derivative of the fiber birefringence vector included in our analysis. As an example, we have shown that the second-order PMD vector components can be Gaussian-like distributed instead of a soliton shape. If the fiber length is scaled by a factor of 2/3, our result obtained for linearly birefringent fibers has the same functional form with the previous joint characteristic function of [13] obtained for fibers having a spherically symmetric birefringence vector distribution in Poincare space.