One goal of visual modeling is to predict the visual performance or a change in performance of an individual from a model of the human visual system [1]. Recent advances in biometric measurement of the eye and in computerization to expedite extensive, complex optical calculations have made it possible to model the optical performance of the eye accurately. Predicting optical image quality at various levels of defocus, contrast, and pupil size can be achieved by calculation of a modulation transfer function and contrast sensitivity function from the model eye [2].
The eye is chromatically undercorrected by approximately 0.5 diopters at both red and green wavelengths, and in general, spherically undercorrected for pupilliary apertures less than 3mm. However, spherical correction for wider eye pupils ranges from several dioptres undercorrection to several dioptres overcorrection [3].
In designing the magnifier and the optical microscope system coupled with the eye, previous optical designers made an optical eyepiece system by inverse ray tracing [4, 5]. This system handled the infinity plane as the object plane, and the object plane as the image plane.
Other designing systems, in which the pupil is matched with the optical system, consider the eye as an ideal lens using the afocal system, and the ray is traced directly. The object displayed plane is treated as the object plane, and the retinal plane as the image plane.
However, the human eye has aberrations that prevent emmetropia. Therefore, proposing to improve the formation of the image at the retina, by an inverse ray tracing method that considers the eye and the method of regarding the human eye as the ideal lens cannot achieve suitable results.
We introduce a new method for lens design that combines the eyepiece with the corrected Navarro eye. We propose a new design method for an afocal system among the two great classifications, focal and afocal, of geometrical optics. Our lens design considers the aberration of the eye and increases the performance of the image in the retina.
In this paper, we demonstrate the corrected Navarro accommodation-dependent finite model eye and the accommo-dation dependence of the vitreous thickness on the visual acuity of the model eye. Visual performances were compared and analyzed for each design method. Our design method would be used as an optical system that considers the aberration of the eye.
2.1 The Corrected Navarro Eye [6]
All optical calculations were performed with the ZEMAXEE optical design and analysis software. Exact ray tracing was involved in all calculations.
The corrected Navarro eye is designed to give emmetropic performance. Anatomically, the pupil is positioned directly in front of the crystalline lens. It is not exactly centered with respect to the rest of the eye and is often displaced slightly nasally by ~0.5 mm [7]. Because of the various aberrations of the eye, this displacement has some effect on image quality and visual performance.
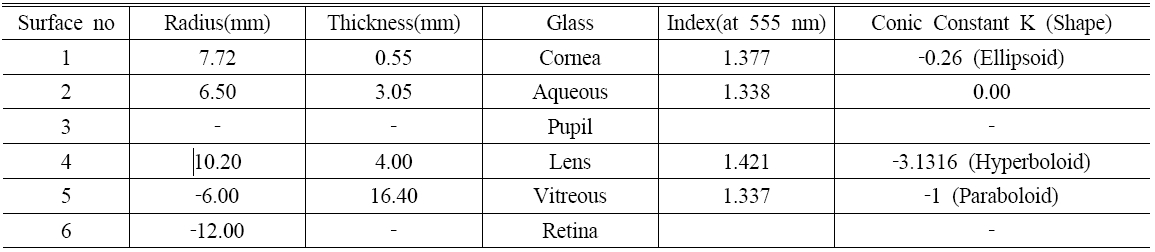
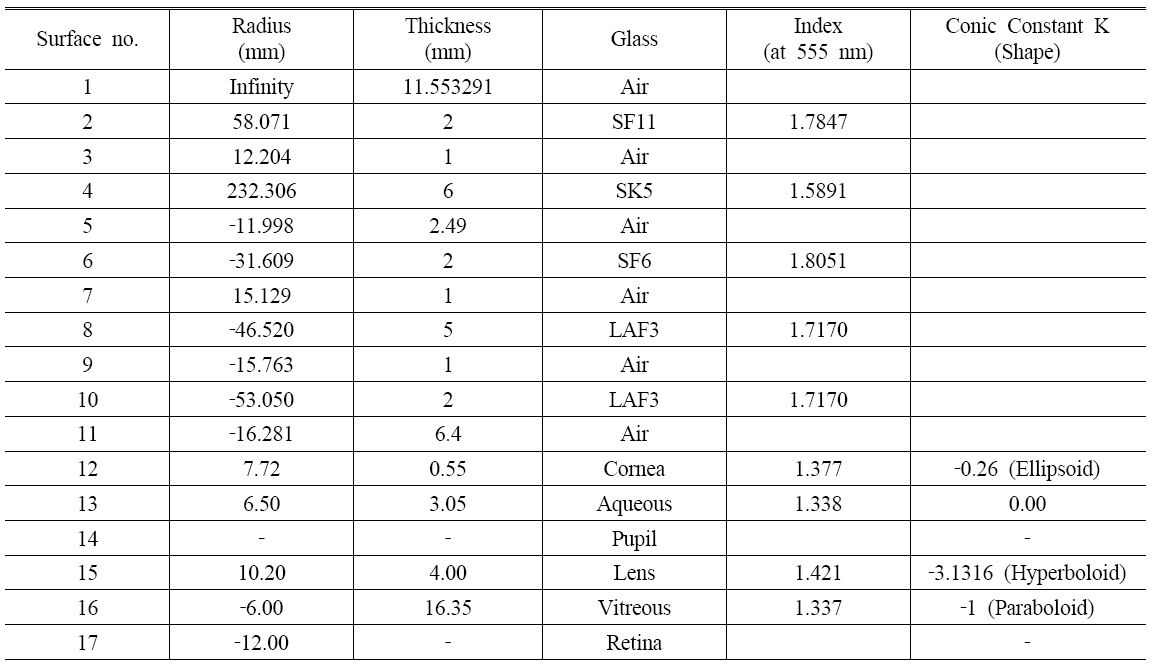
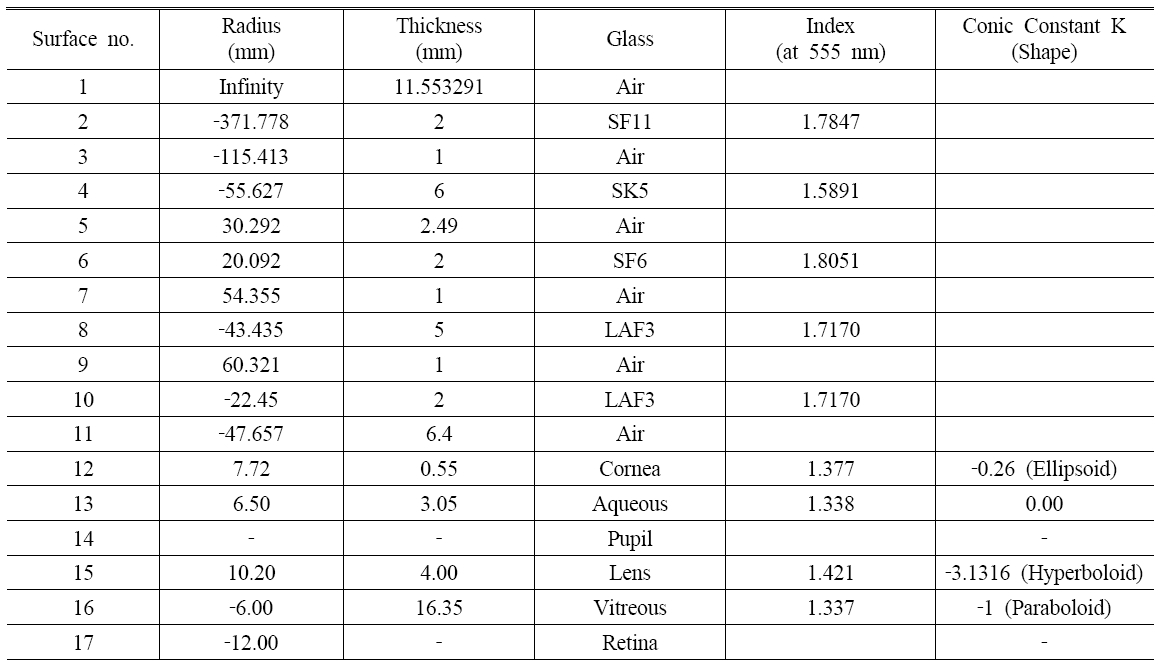
Table 1 lists all the parameters of the corrected Navarro eye, and Figure 1 illustrates the schematic features of the corrected Navarro eye and shows the directions of angle alpha and pupil decentration. The upper side is the temporal direction from the optical axis, and the lower part is in the nasal direction. The pupil diameter is 4 mm. Details regarding Table 1 are as follows. Surface no.3 contains the aperture stop, that is the pupil, whose center is decentered by 0.5 mm nasally. For calculations of the modulation transfer-function (MTF), angle alpha was incorporated by using a pencil of rays directed toward the center of the entrance pupil at an angle of 5° nasally from the optical axis [2]. Aspheric surfaces on the anterior and posterior surfaces of both the cornea and lens are represented by conicoids. A conicoids can be expressed in the form:
where the Z axis is the optical axis, h2=X2+Y2. R is the vertex radius of curvature and Q is the surface asphericity.
The corrected Navarro eye also includes a retinal effect known as the Stiles-Crawford effect. We applied apodization in the pupil to express the Stiles-Crawford effect that happens in the retina optically and we used an apodization coefficient of 0.12mm-2. Lens designs used wavelengths of 470, 510, 555, 610, and 650 nm with weightings of 0.091, 0.503, 1, 0.503, and 0.107 respectively. The effective focal length of the corrected Navarro eye is 16.46 mm in air and the total optical pass distance (OPD) of the eye is 23.95 mm.
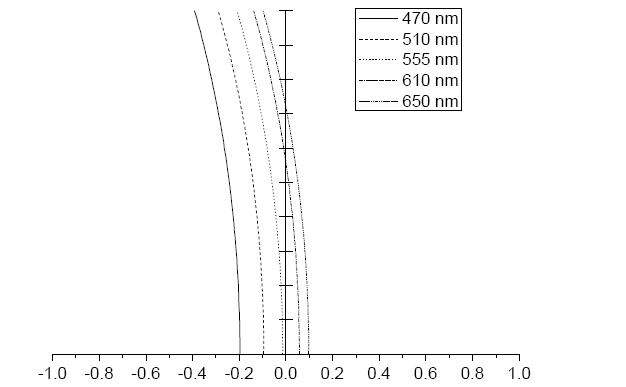
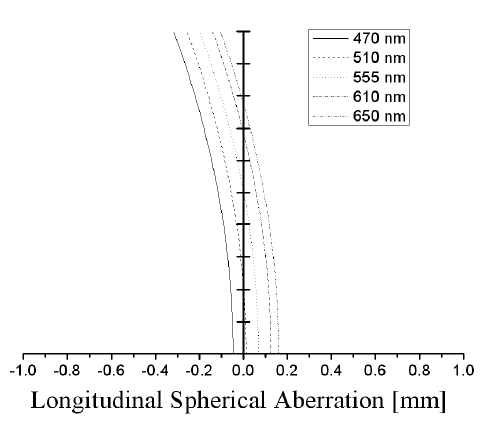
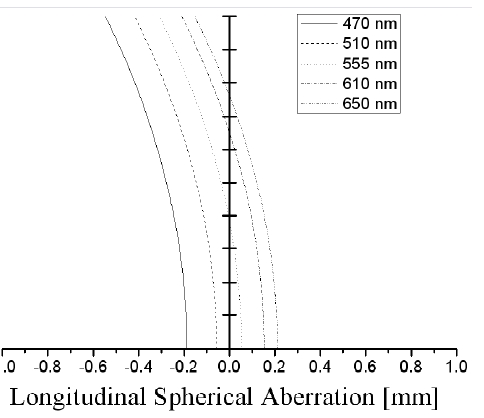
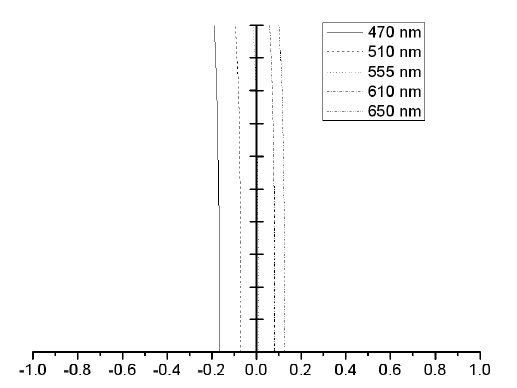
Figure 2 shows the calibrated longitudinal aberration of
[TABLE 1.] Lens prescription for the corrected Navarro Eye
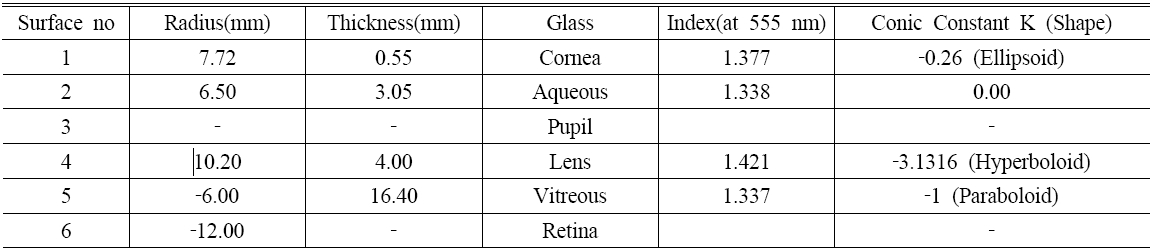
Lens prescription for the corrected Navarro Eye
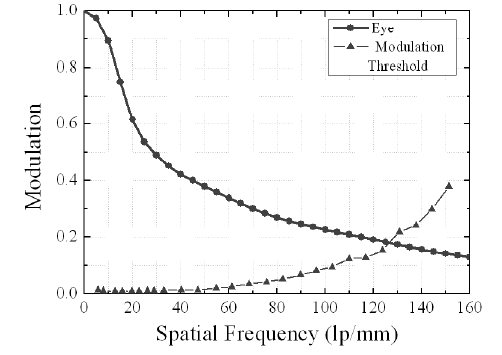
the corrected Navarro eye in the visible wavelength range. The Seidel aberration coefficients in waves W040 is 1.521. Figure 3 shows the square-wave modulation transfer function (SMTF) of the corrected Navarro eye in the visible wavelength range. The retinal contrast sensitivity function is the reciprocal of the modulation threshold function. The modulation threshold was adapted from the results of Campbell and Green [8]. The spatial frequency where the curves intersect is an estimate of the visual acuity. The intersection of the SMTF and the modulation threshold at 126 lp/mm determines the spatial frequency of a barely resolvable bar target.
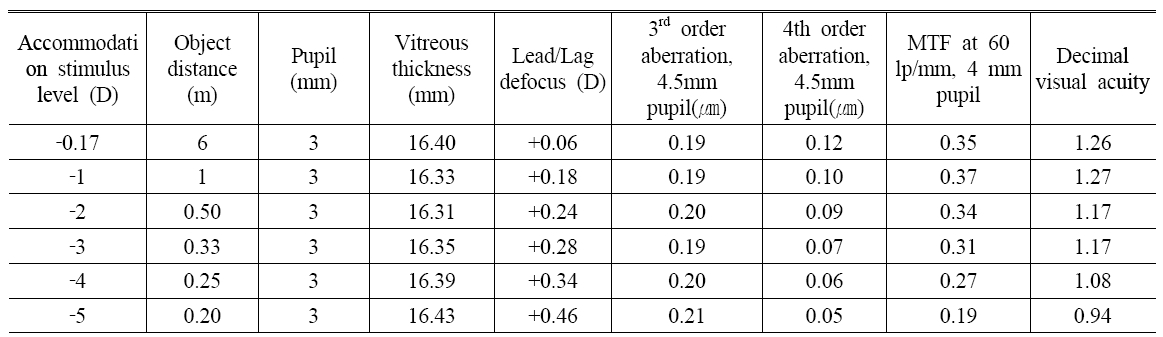
Table 2 lists the accommodation dependence of the lens parameters on accommodation A (in diopters). The accommodation dependence of the vitreous thickness was obtained by fitting the variation of the vitreous thickness onto the accommodation-stimulus. The accommodated eye's visual performance, including the accommodation response by the accommodation-stimulus, was obtained in this way. Vitreous thickness varied to correct the error of total refractive power, so it acted to remove the error. The total optical length of the eye, including the variation of the vitreous thickness, had a value between 23.89 mm and 24.08 mm. The total optical length of eye remained approximately 24 mm in spite of the variation of the accommodation-stimulus.
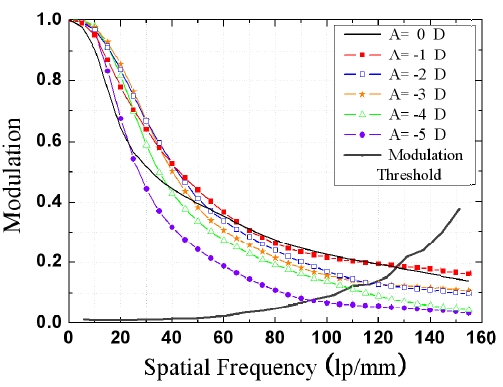
In Table 3, all vitreous thickness, accommodation lead and lag defocus, 3rd and 4th order aberration, Modulation transfer function, and visual acuity results for each of the six accommodation levels are summarized for both fixed 3-mm pupil sizes. Figure 4 shows the SMTF for the corrected Navarro eye with a 4 mm pupil along with a plot of the modulation threshold. The result is the decimal visual acuity of Table 3.
A new novel model eye was designed using a Navarro accommodation-dependent finite model eye. For each of the vergence distances, ocular wavefront error, accommo-dative response, and visual acuity are calculated. Using the new model eye ocular wavefront error, accommodation dative response and visual acuity are calculated for six vergence stimuli, -0.17 D, -1 D, -2 D, -3 D, -4 D, and -5
[TABLE 2.] Accommodation dependence of the lens parameters on accommodation A (in diopters).

Accommodation dependence of the lens parameters on accommodation A (in diopters).
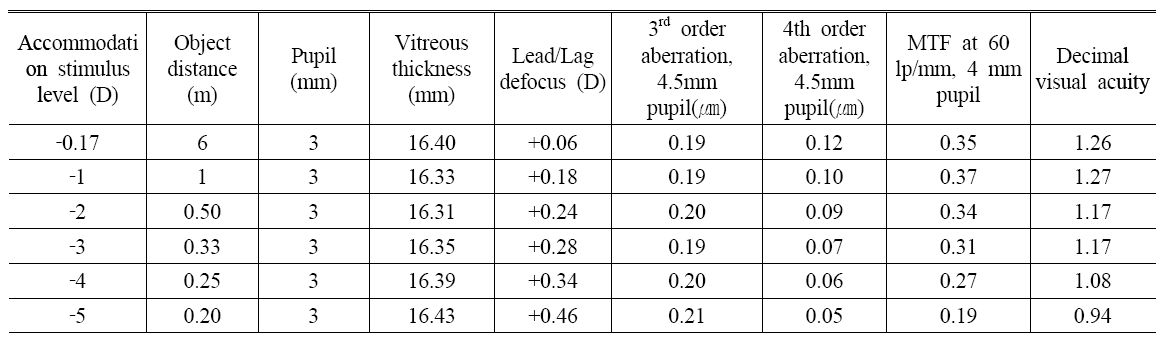
Visual performance in the corrected Navarro eye for the six accommodation stimulus levels.
D. Also, 3rd and 4th order aberrations, modulation transfer function, and visual acuity of the accommodation-dependent model eye are analyzed. These results are well matched to anatomical, biometric, and optical realities [6].
2.2 Lens Design of Eyepiece
The eyepiece is based on a lens reported by Cheon Seog Rim in 1994 [9]. This lens was designed by the following 4 steps: 1) Gauss optical analysis, 2) lens design by the Seidel third order aberration theory, 3) finite ray aberration’s optimization using computer, and 4) final estimation via resolution of the eye in the image surface (virtual image). Optimization of the eyepiece overturned to the right and left and was enforced.
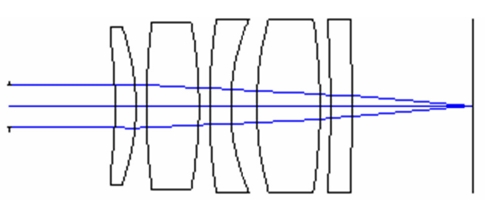
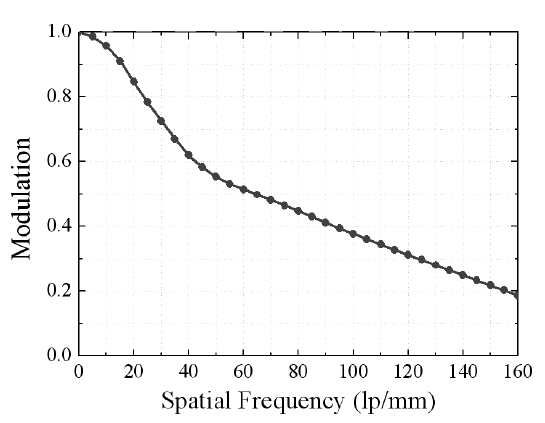
An optical glass was preappointed, and optimization variables were limited to the lens curvatures and thicknesses. Rim’s optimization results were as follows. Figure 5 shows the Rim’s optical layout of the inverse ray tracing designed eyepiece. Figure 6 shows the calibrated longitudinal aberration. The Seidel aberration coefficients in waves W040 is 0.896. Figure 7 shows the square-wave modulation transfer function (SMTF) in the visible wavelength range. It can be seen that the SMTF is near 0.2 at 160 lp/mm.
Our method takes one of the eyepiece designs and combines it with the model eye for analysis. The method is as follows. The eyepiece configuration (Fig. 5) must be reversed prior to the addition of the corrected Navarro eye (finite model eye). The first surface (the entrance pupil) of the resulting lens combination is set at a distance of 11.553291 mm from the object. This results in the chiefrays entering the eyepiece at a +5 deg angle, consistent with the original eyepiece design data. The corrected Navarro eye is located with its first surface (outer surface of the cornea) 3.6 mm inside the exit pupil of the eyepiece. This results in the entrance pupil of the eye being superimposed on the exit pupil of the eyepiece [10]. The resulting lens system is shown in Figure 8, with longitudinal aberration curve (Fig. 9) and
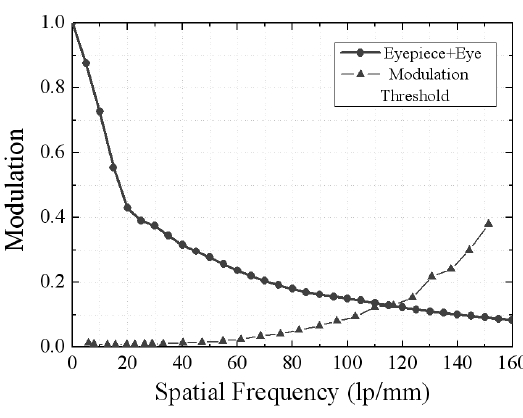
lens prescription (Table 4). The Seidel aberration coefficient in waves W040 is 3.005. Figure 10 shows the square-wave modulation transfer function (SMTF) in the visible wavelength range. It can be seen that the SMTF is near 0.1 at 160 lp/mm. Also, the SMTF and the modulation threshold intersect at 115 lp/mm. This corresponds to visual acuity 1.15 [12]. This is lower than the MTF value of the single eyepiece seen in Figure 7 because the eye’s aberration and the eyepiece were calculated together. Finally, we can confirm by later adding the designed eyepiece's aberration to the eye’s aberration that the MTF value in the retina becomes low.
The optical system consisted of the eyepiece of initial
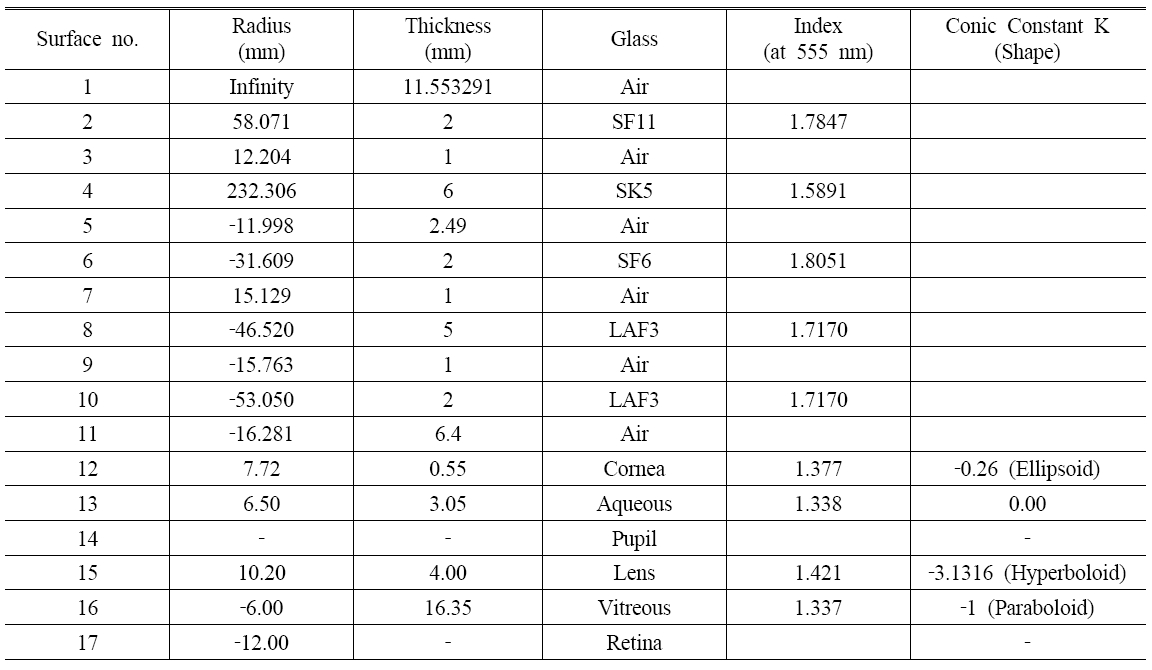
Lens prescription of the inverse ray tracing designed eyepiece with the corrected Navarro eye
design (Lens design by the Seidel third order aberration theory) in front of the corrected Navarro eye (Table 5; Surface no. 12-17). Also, the entrance pupil of the eye was superimposed on the exit pupil of the eyepiece. The optical glass and thickness are same as the value of the inverse ray tracing designed eyepiece with the corrected Navarro eye (Table 4). We optimized the eyepiece with the optimization variables limited to the ten lens curvatures (Table 5; Surface no. 2~11).
The purpose of optimization is to give aberration to aneyepiece. This aberration compensates for the eye's aberration.We analyzed a spherical aberration that causes a
[TABLE 5.] Lens prescription for the optimized eyepiece combined with the corrected Navarro eye
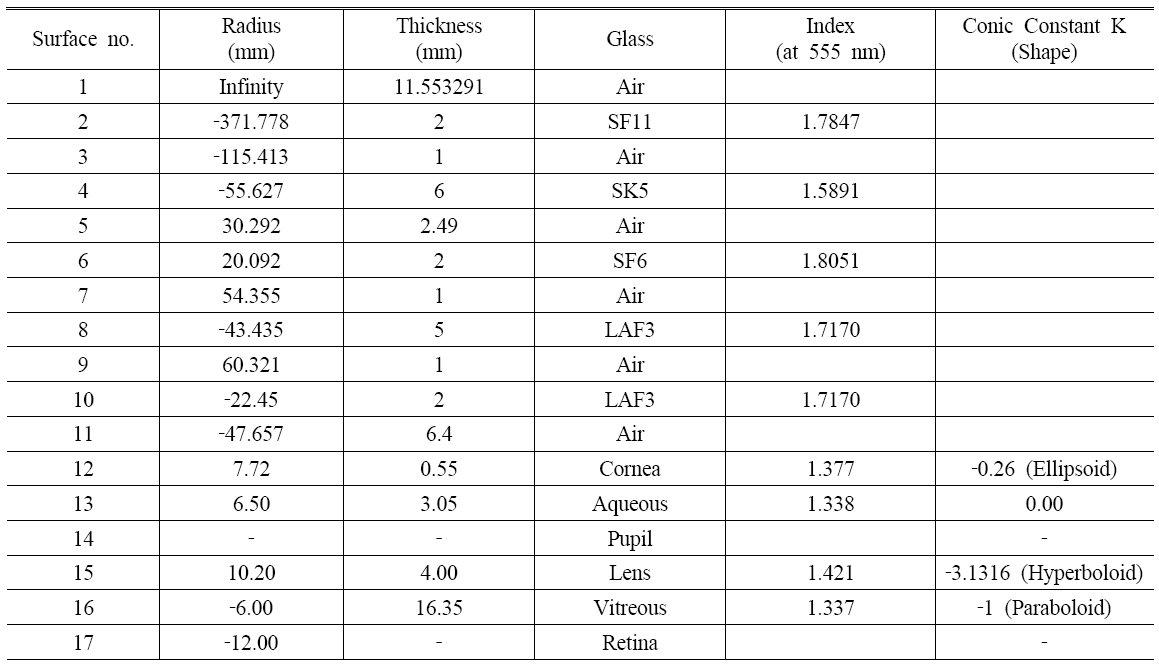
Lens prescription for the optimized eyepiece combined with the corrected Navarro eye
big effect in performance representatively [6]. The Seidel aberration coefficient of the corrected Navarro Eye in waves W040 is 1.521 (Fig. 2). The Seidel aberration coefficient of the inverse ray tracing designed eyepiece in waves W040 is 0.896 (Fig. 6). The Seidel aberration coefficient of the inverse ray tracing designed eyepiece with the corrected Navarro eye in waves W040 is 3.005 (Fig. 9). Each plus aberration value of the eye and eyepiece was added. Therefore, if the eyepiece has a minus value, aberration of eye is compensated for. The resulting lens system is shown in Figure 11, with longitudinal aberration curve (Fig. 12) and lens prescription (Table 5). The Seidel aberration coefficient in waves W040 is 0.011. The Seidel aberration coefficient in waves W040 of the eyepiece at this system is -0.927. The Seidel aberration coefficient of the eyepiece had minus value, so the aberration of the eye was compensated for. The Seidel aberration coefficient of
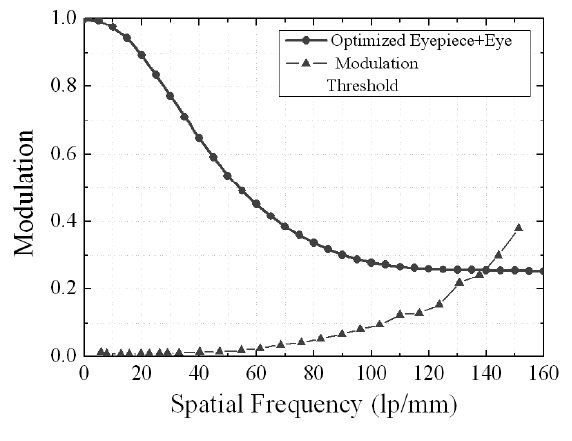
the optimized eyepiece combined with the corrected Navarro eye was decreased. Figure 13 shows the squarewave modulation transfer function (SMTF) in the visible wavelength range. It can be seen that the SMTF is near 0.3 at 160 lp/mm. The SMTF and the modulation threshold intersect at 140 lp/mm. This corresponds to visual acuity 1.40. When compared with the inverse ray tracing designed eyepiece with the corrected Navarro eye (Fig. 10), MTF value confirmed by 0.079 to 0.283 at 160 lp/mm that performance improves.
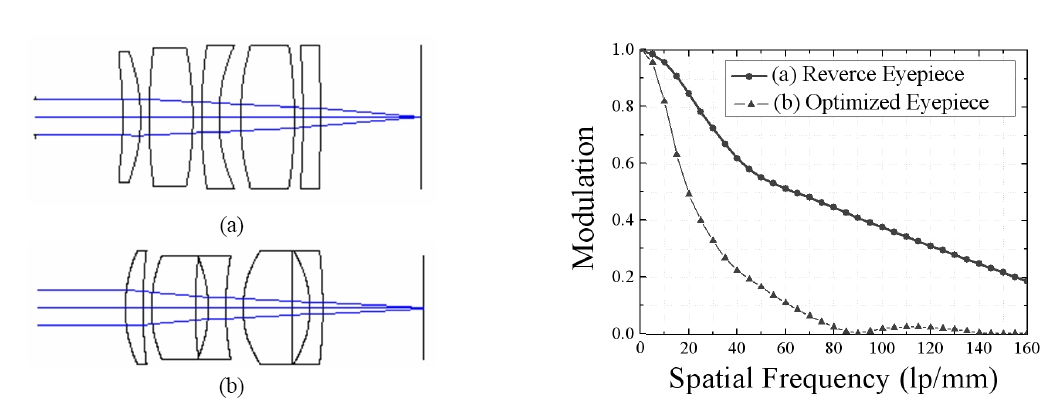
Figure 14 shows the optical layout and the SMTF. (a) is the inverse ray tracing designed eyepiece. (b) is the eyepiece from the optimized result combined with the corrected Navarro eye. The MTF performance of Figure 14 (b) is lower than that of 14 (a) because 14 (b) has a bigger aberration. However, this aberration is compensated for with the model eye. Finally, MTF performance in the retina is bigger. This comparison shows that the most suitable retinal image is achieved when the model eye is included.
Figure 15 shows retinal image quality of the inverse ray tracing designed eyepiece with the corrected Navarro eye (Fig. 8) and the optimized eyepiece combined with the corrected Navarro eye (Fig. 11). Retinal image recon
struction is convolution of Snellen E with a Gaussian point spread function (PSF) [11]. The pupil diameter is 4 mm and the relative Snellen Acuity is 20/20. Intensity distribution is a simulated vertical intensity profile through the blurred bars of a Snellen E. The brightest intensity (IMAX) and the darkest intensity (IMIN) are used to calculate the modulation in the blurred image. Size of the point spread function is 63.75 ㎛ × 63.75 μm. The point spread function is normalized. The size or width of overlapping PSFs determines the amount of image blur, and this PSF width can be used as measure of the performance of an optical system. Airy disk diameter of the inversed method is bigger. This becomes a factor which lowers resolution. Image reconstruction of the optimized eyepiece combined with the corrected Navarro eye shows a better retinal image compared with the inverse method.
We demonstrated the corrected Navarro accommodationdependent finite model eye and the accommodation dependence of the vitreous thickness considering the visual acuity of the model eye. We introduced a new method for lens design that combines the eyepiece with the corrected Navarro eye. Our lens design considers the aberration of the eye and increases the performance of the image in the retina.
In the design results, at the optimized eyepiece combined with the corrected Navarro eye, visual acuity is 1.40. Compared with the existing method of eyepiece design using inverse ray tracing with the corrected Navarro eye, MTF value was recorded by 0.079 to 0.283 at 160 lp/mm and the visual performance was improved. With these results, we present the possibility of a newly proposed design method.
In further work, we will try to combine our design method with other optical systems. The designed optical system will be actually manufactured and its visual performance will be measured. Also, the binocular factor is will be studied together and applied to the design of the binocular optical system.