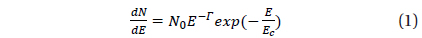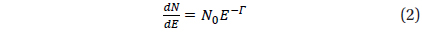Together with an improved pulsation search algorithm (e.g., Kerr 2011), the large area telescope (LAT) onboard Fermi γ-ray Space Telescope has significantly enlarged the population of γ-ray pulsars with its unprecedented sensitivity. In the second Fermi LAT pulsar catalog (2PC Abdo et al. 2013), 117 pulsar detections at energies > 100 MeV are reported using three years of data. It comprises 42 radio-loud (RL) pulsars, 35 radio-quiet (RQ) pulsars and 40 millisecond pulsars (Abdo et al. 2013)1. It should be noted that the fractions of RL and RQ are comparable in the known γ−ray pulsar population. However, the true RL/RQ fractions can be different from the observed values in the presence of various selection effects. For example, blind searches for RQ pulsars can only be performed in high energy regimes, which are photon-limited. On the other hand, in the case of searching RL γ-ray pulsars, one can utilize the ephemeris obtained in radio. This implies that the intrinsic RQ fraction can be larger than the observed one by ~30%. In a recent study, Sokolova & Rubtsov (2016) estimated that the intrinsic fraction of radio-quiet γ−ray pulsars can be as large as ~70%.
Knowing the true fraction of RQ is important for constraining the pulsar emission models. The outer-gap model suggests that γ−rays originate from the outer magnetosphere and form a fan beam (see Cheng & Zhang 1998; Takata et al. 2006, 2008). On the other hand, the radio emission forms a narrow cone when it originates from the polar cap region (Kijak & Gil 1998, 2003). The ratio of RL and RQ populations can help us to constrain the emission and viewing geometry. As RL and RQ pulsars form two distinct populations, a number of investigations have compared the properties of these two classes. Marelli et al. (2011, 2015) and Marelli (2012) found the difference between these two populations in terms of the γ−ray-to-X-ray flux ratio Fγ/FX. Fγ/FX of the RQ population was found to be significantly higher than that of the RL population. Sokolova & Rubtsov (2016) also reported a possible difference in the distributions of their rotation periods. Very recently, Hui et al. (2016) examined the various physical properties of RQ and RL γ−ray pulsars. Among all the possible differences found in these two populations, the most significant is the curvatures of their γ−ray spectra.
Using various different properties identified for RQ and RL pulsars, we suggest a method to estimate the intrinsic fraction of radio-quietness in the population of γ−ray pulsars. In the third Fermi γ−ray point sources catalog (3FGL; Acero et al. 2015), among 3,033 sources detected at a significance > 4σ, more than 1,000 sources do not have any known counterparts at other energy bands. Using the γ−ray properties of pulsars (e.g., variability, curvature significance, locations in our galaxy) together with the machine learning techniques, Saz Parkinson et al. (2016) selected a group of pulsar-like unidentified γ−ray sources and further classified them into the categories of young pulsars and millisecond pulsars. Applying the same techniques together with the aforementioned features that can distinguish the RQ and RL pulsars, it is feasible to select the non-recycled pulsar candidates from the unidentified source population and classify them into RQ or RL classes. This can provide a less biased estimate for the radio-quietness fraction. In this paper, we discuss the possibility of using the γ−ray spectral shape to distinguish RQ and RL pulsars.
The γ−ray spectra of pulsars are characterized by the form of a power-law with an exponential cut-off (PLE),
where N0, Γ, and EC are the normalization, photon index, and cut-off energy, respectively. This is signaificantly curved in comparison with a simple power-law(PL):
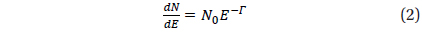
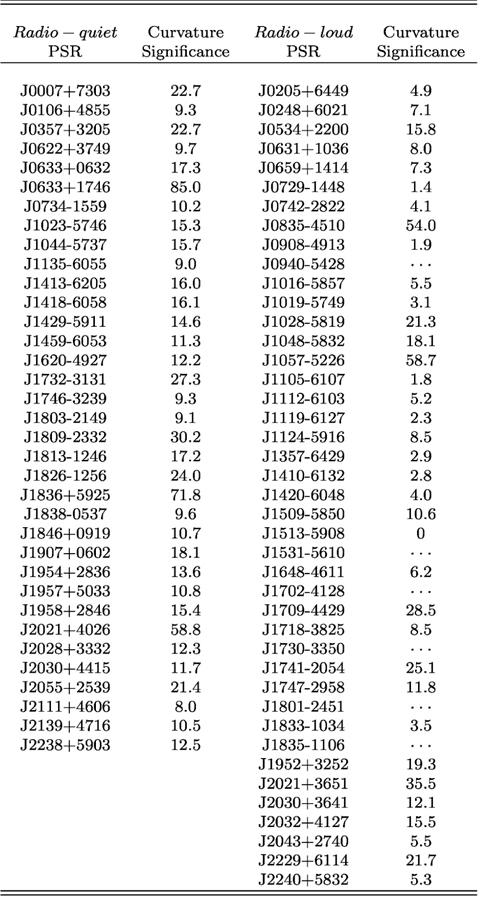
In the 3FGL catalog, the curvature of the pulsars’ γ-ray spectra is quantified by the parameter Curve Significance, which is obtained by comparing the difference between the PLE and PL model fittings in unit of σ. Using the K-S test, Hui et al. (2016) found that the distributions of Curve Significance show the most significant difference between RQ and RL pulsars among all the tested parameters. The difference is found at a confidence level of > 99.999%. In Table 1, we have tabulated the Curve Significance for all the non-recycled RQ nad RL pulsars in 2PC. All the data in this table are collected from 3FGL (Acero et al. 2015). Hui et al. (2016) showed histograms of Curve Significance for both populations. Using these distributions, we can compute the posterior probabilities of being RQ (P(RQ|Cur)) or RL (P(RL|Cur)) for a given Curve Significance.
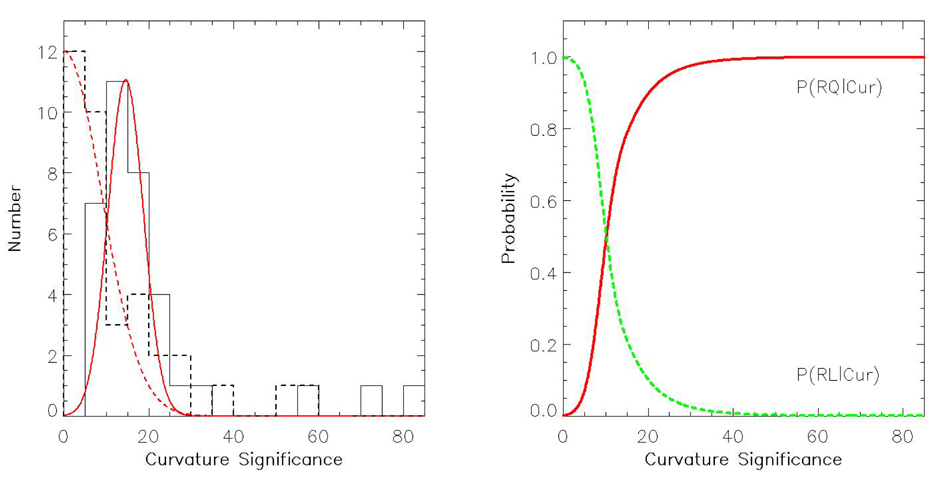
In examining the distributions reported by Hui et al. (2016), we notice the fluctuations appear at the large values of Curve Significance. This can be ascribed to the small statistics in this range. For a simple parametric estimation of the underlying probability density function, we suppress these noises by fitting the histograms with Gaussian models with the following form:
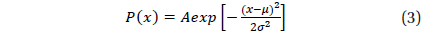
where A, μ, and σ are the parameters that depict the peak, the mean, and the width of the model, respectively. For the RQ population, all three parameters, A, μ, and σ, are set to be free in the fitting. For the RL population, visual inspection clearly indicates that the peak and the mean are located around zero Curve Significance. Therefore, A and μ are fixed and we only let the width of the function σ be free. The best-fit functions are shown in the left panel of Fig. 1, which provides a reasonable approximation of the distributions. Using these estimates of probability density functions, we further construct the posterior probabilities P(RQ|Cur) and P(RL|Cur) and have shown them in the right panel of Fig. 1.
As γ−ray spectral curvatures of non-recycled RQ and RL pulsars in 2PC are found to be significantly different (Hui et al. 2016), one can use this aspect as an additional feature in classifying those sources that have no known multi-wavelength counterparts. To facilitate the classification, we have computed P(RQ|Cur) and P(RL|Cur), which can help to estimate the probability of any non-recycled pulsar-like candidate being RQ or RL by giving its Curve Significance.
We strongly believe such investigation as this can provide a less biased estimate of the intrinsic fraction of radio-quietness. By performing a blind pulsation search for all point sources in 3FGL with Fermi LAT data alone, Sokolva & Rubtsov (2016) estimated the radio-quietness fraction to be єRQ = 63 ± 8%. The catalog they compiled is free from the bias as RL pulsar search can utilize the information through radio observations. However, one should note that blind search of such a large sample is computationally demanding. On the other hand, our proposed method can provide an independent estimate by using the spectral curvature. Combining the spectral feature with the method of selecting pulsar candidates (e.g. see Fig. 1 in Hui et al. 2015), one may estimate єRQ simply using Curve Significance, P(RQ|Cur) and P(RL|Cur) as inputs.
The aforementioned comparison of the γ−ray spectral curvature is only for the non-recycled pulsars. There is no existing literature on a similar analysis of millisecond pulsars (MSPs). It will be interesting to compare the spectral features and other γ−ray properties of MSPs with those of non-recycled RQ and RL pulsars. This kind of study can help to search for the possible features that can make the MSP candidate selection more accurate (see Hui et al. 2015). Also, to date, no MSP has been found to be RQ. Through such comparison, one may draw insights on the expected properties of RQ MSPs, if they exist.
Finally, we would like to stress that the density estimation in this work is obtained through a simple parametric estimation and limited by the relatively small sample size. With an enlarged γ−ray pulsar population in the future, our estimation can be improved by employing a more sophisticated method of density estimation (e.g., using kernels).