Properties of single walled carbon nanotubes (SWCNTs) are defined by their diameter, length, chirality/twist, and nature of the wall. However, there are also some distinctive properties of SWCNTs, such as their surface area, stiffness, strength, and resilience, which have led to a wide range of technological applications in mechanical materials, optics, and electronics. Making changes to their properties is very challenging. It is very difficult to synthesize SWCNTs with uniform chirality and well defined electronic properties. The difficulty can be adjudicated by introduction of dopants that modify the electronic properties of SWCNTs [1-6]. Studies have uncovered that nitrogen doping is uniquely attractive as nitrogen has roughly the same atomic radius as carbon atoms and its extra electrons make semiconducting nanotubes metallic.

Carbon nanotubes (CNTs) can serve as an excellent medium to address some quantum phenomena related to size effects such as ballistic transport, super-current, and universal conductance fluctuations [7]. It is necessary to further address whether the transport of CNTs is controlled by a ballistic or diffusive mechanism. Furthermore, we should analyze how doping affects the electronic properties of CNTs, as doping play an important role in band gap design engineering [8]. Since 1968, energy band engineering techniques such as doping have played an important role in the electronics industry in terms of increasing the conductivity of silicon or germanium materials [9]. In the past decade there has been a great deal of interest in doping CNTs by different techniques to identify the hidden characteristics of CNTs [10,11].The electronic properties of CNTs can be intentionally modified. CNTs have a unique morphology, and there is a wide variety of possible approaches to dope them and thereby alter their physical and electronic properties. Through a proper choice of the type of modification, including doping, the electronic properties of CNTs can be tuned to a great extent. Many doping approaches take advantage of the molecular nature of the nanotubes; however, it is also possible to dope in the more traditional sense, i.e., intentionally replacing CNTs with impurities. The electronic properties of nitrogenated SWCNTs were studied using extended Hückel theory (EHT) with nonequilibrium Green’s function, and the obappretained results demonstrate that the electronic properties of the SWCNTs are strongly dependent on the dopant concentration.

In this paper we have investigated quantum confinement effects on the electronic properties of SWCNTs. The physical, chemical, electrical, and optical properties of any solid can be determined by its quantized electronic states. These quantum states in nano-scale systems are brought forth due to the confinement of charge carriers or molecules in 1-D or 2-D. In our model, we have confined a H₂ molecule in an (8, 0) semiconducting SWCNT and we study the confinement effects on the electronic properties. This paper is organized into four sections. Following the introduction presented in section 1 above, section 2 presents the modeling and simulation approach and section 3 provides the simulation results. Section 4 concludes the paper.

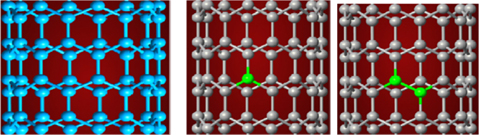
Modeling and simulation provide information regarding how something will behave without testing. Modeling is the process of producing a model; a model is a representation of the construction and working of a system of interest, and the model is similar to but simpler than the system it represents. One purpose of a model is to enable an analyst to predict the effects changes to a system. A model should be a close approximation of the real system and incorporate most of its salient features. A simulation of a system is the operation of a model of the system. The model can be reconfigured and experimented with. The operation of the model can be studied and hence properties concerning the behavior of the actual system or its sub-systems can be inferred. Simulation is a tool to evaluate the performance of a system proposed under different conditions. Pure and nitrogen doped (8, 0) single walled CNTs are schematically illustrated in Fig. 1.

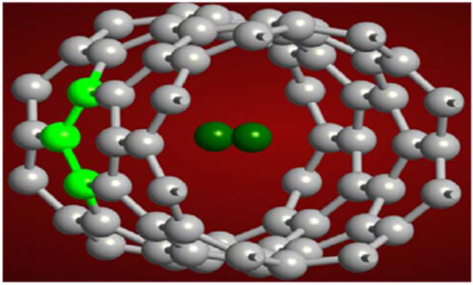
Fig. 2 show a schematic illustration of a H2-confined nitrogenated carbon nanotube. The hypothesis for this confinement is based on nonequilibrium Green’s function formulation [12]. We have also used the semi-empirical extended Hückel theory approach [13]. In commencing the simulation, we used the following parameters. These parameters were taken to achieve an optimal combination of accuracy and speed of the calculations (Table 1).

In order to understand the effects of dopants on the electronic properties of zigzag (8, 0) SWCNTs, the proposed models were simulated using the Atomistic ToolKit ver. 13.8.1 (Quantum-Wise, Copenhagen, Denmark) and its graphical interface (custom analyzer) virtual nano lab [14]. The simulations were performed at different dopant concentrations. The band structures for all simulated models were analyzed by taking energies at the vertical axis at arbitrary units (Fig. 3).

It is seen that the energies depend on the concentration of nitrogen atoms. Therefore, we increased the number of doped nitrogen atoms. Upon nitrogenation, the degeneracy of the energy bands of (8, 0) nanotubes are lifted, the presence of nitrogen impurities causes the band to split. As the concentration of nitrogen atoms is increased to 2 atoms, we noticed a sharp splitting of the band and the impurity state of nitrogen contributes mainly to the conduction band minimum. The valance and the conduction bands cross each other at the Fermi level, which is in agreement with previous results [14-16]. Energy band splitting engineering techniques have played a vital role in tuning the band gap of CNTs.

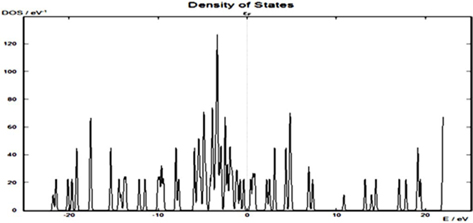
To investigate the effects of nitrogen impurities, we also calculated the density of states (DOS) of a (8, 0) SWCNT without the nitrogen dopants. The DOS of a pure (8, 0) semi-conducting SWCNT is shown in Fig. 4.

Previous investigations reported that pyridine-like dopants in CNTs are energetically favorable and doping can take place at high synthesis temperature; therefore we prepared pyridine-like dopants and used them to dope SWCNTs, which are useful in designing nitrogen doped CNT based devices.

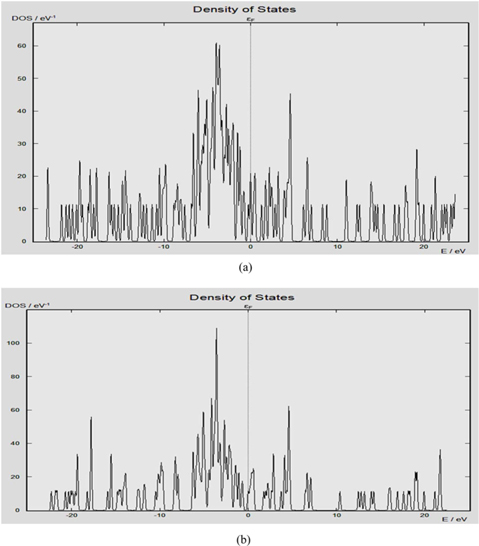
In Fig. 5, we present the DOS of nitrogen doped (8, 0) semiconducting SWCNTs. The graph depicts that a small dopant concentration of around 1.042% pyridine-like substitution of nitrogen narrows the band gap. As the dopant concentration is increased, the band gap increasingly narrows and is finally filled with impurity states as the dopant concentration becomes appretained ciably large. We have also analyzed that at a dopant concentration of around 2.083% the nanotubes become metallic due to the impurity states at the Fermi level.

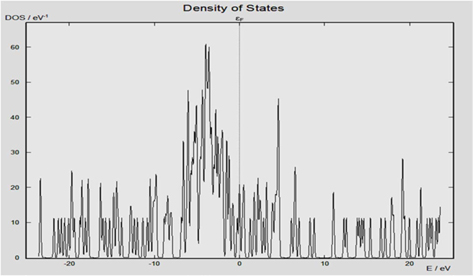
Moreover, we have entrapped a hydrogen molecule within an (8, 0) nanotube to identify the quantum confinement effects on the electronic properties of SWCNTs. The bond length of the hydrogen molecule is fixed so that the motion of the atoms ceases within the CNT. The interactions between the hydrogen molecule and the CNT are dispersion interactions. Density functional theory cannot compute such interactions. Therefore, the EHT approach, a semi-empirical formalism, is used to study these interactions. The DOS in a zigzag (8, 0) H₂-confined nitrogenated CNT is presented in Fig. 6.

From Fig. 6, we observed sharp dense peaks near the Fermi level, and this illustrates modification of electronic properties by entrapping a H₂ molecule within a CNT. We believe that this approach provides a robust means of transforming semiconducting nanotubes into metallic nanotubes.

The investigated electronic properties of SWCNTs are strongly dependent on the dopant concentration. Upon nitrogenation, the semiconducting (8, 0) nanotubes convert into metallic nanotubes. We observed that the electronic properties were effectively modified by confining a H2 molecule within a CNT. The hydrogen confinement significantly enhances the DOS in the vicinity near the Fermi level.