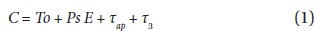CW Cep is a well-known apsidal motion binary system observed by many investigators (Abrami & Cester 1960; Nha 1975; Han et al. 2002; Wolf et al. 2006) since its discovery by Petrie (1947) as a double lined spectroscopic eclipsing binary. The spectral types of two components of CW Cep were determined as B0.5 + B0.5, and masses were calculated as 11.7 M⊙ and 11.0 M⊙ by Popper (1974). The light curves were analyzed by many authors using well observed full-light curves with different models for the parameters of the binary system, related with its apsidal motion (Cester et al. 1978) with the WINK model, Clausen & Giménez (1991) by the EBOP model, and Terrell (1991), and Han et al. (2002) by the WD model. While Popper & Hill (1991) discussed the radial velocity curve based on the spectroscopic observations by Popper (1974), high resolution IUE observations for the radial velocity curve were made by Stickland et al. (1992). Most of these studies suggested that CW Cep is a detached main sequence binary system, composed of two stars of slightly different mass and radius.
With regard to the apsidal motion study of the close eclipsing binary systems, CW Cep showed one of the shortest apsidal period, among similar binary systems, which leads particular interests for this binary system. Based on intensive photoelectric observations with
It is nearly 10 years since the observations by Wolf et al. (2006), and this indicates the necessity of new observations for this binary system to examine more accurate apsidal motion period. In line with this, we made new observations for CW Cep in the 2015 season and obtained three new times of minimum lights to confirm the apsidal motion period of this system, together with available minimum times from the published literatures.
New CCD photometric observations presented in this work were made in the 2015 observational season at the Jincheon station of Chungbuk National University Observatory (CBNUOJ), Korea. The altitude of the Jincheon station is 87 m sea level and the 60-cm reflecting telescope is installed by Korea Astronomy and Space Science Institute (KASI), and operated by CBNUOJ. An electronically cooled SBIG STX- 16803 4K CCD camera is equipped with a Johnson standard
[Table 1.] The times of minimum lights of CW Cep
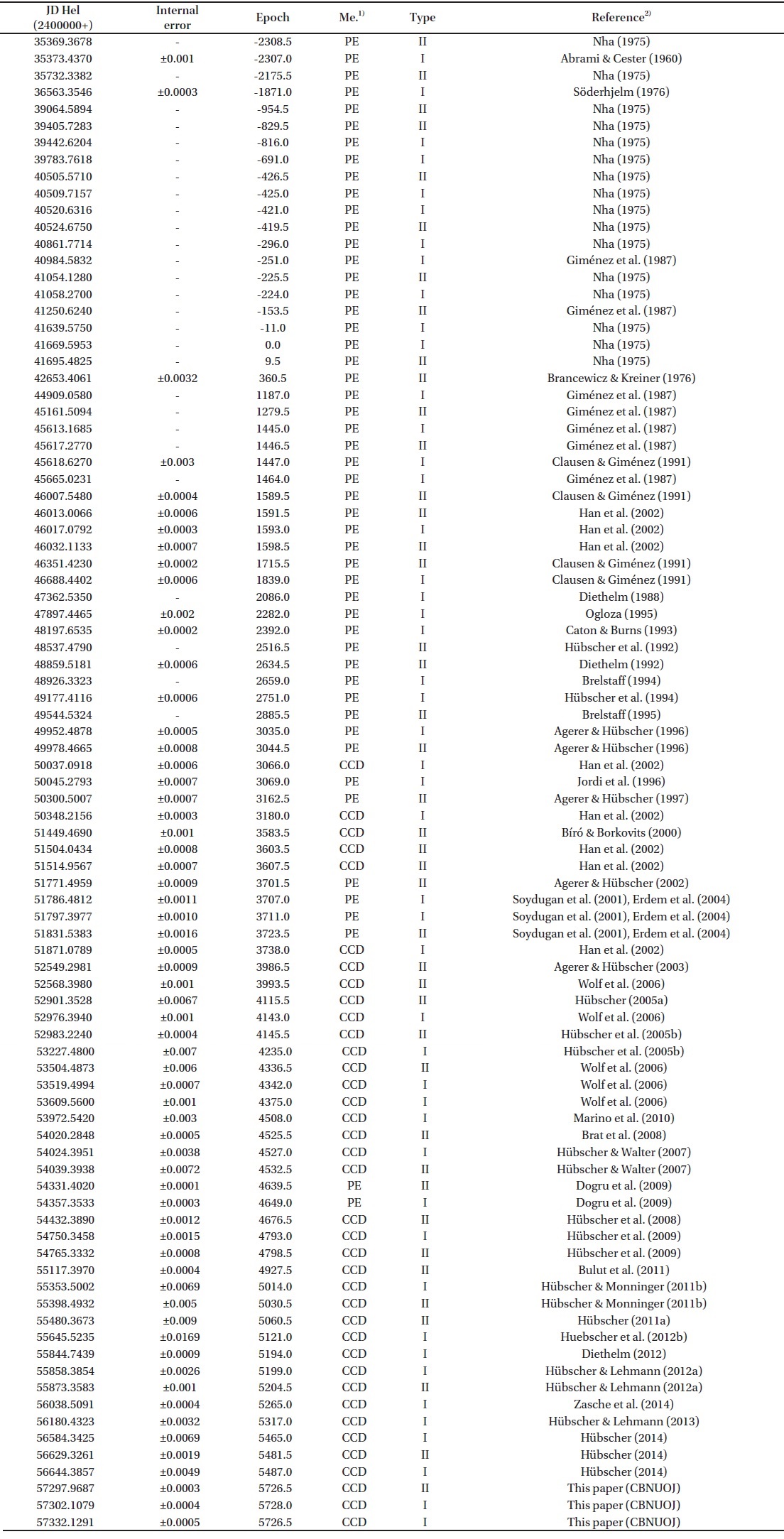
The times of minimum lights of CW Cep
3. MINIMUM LIGHTS AND O-C DIAGRAM
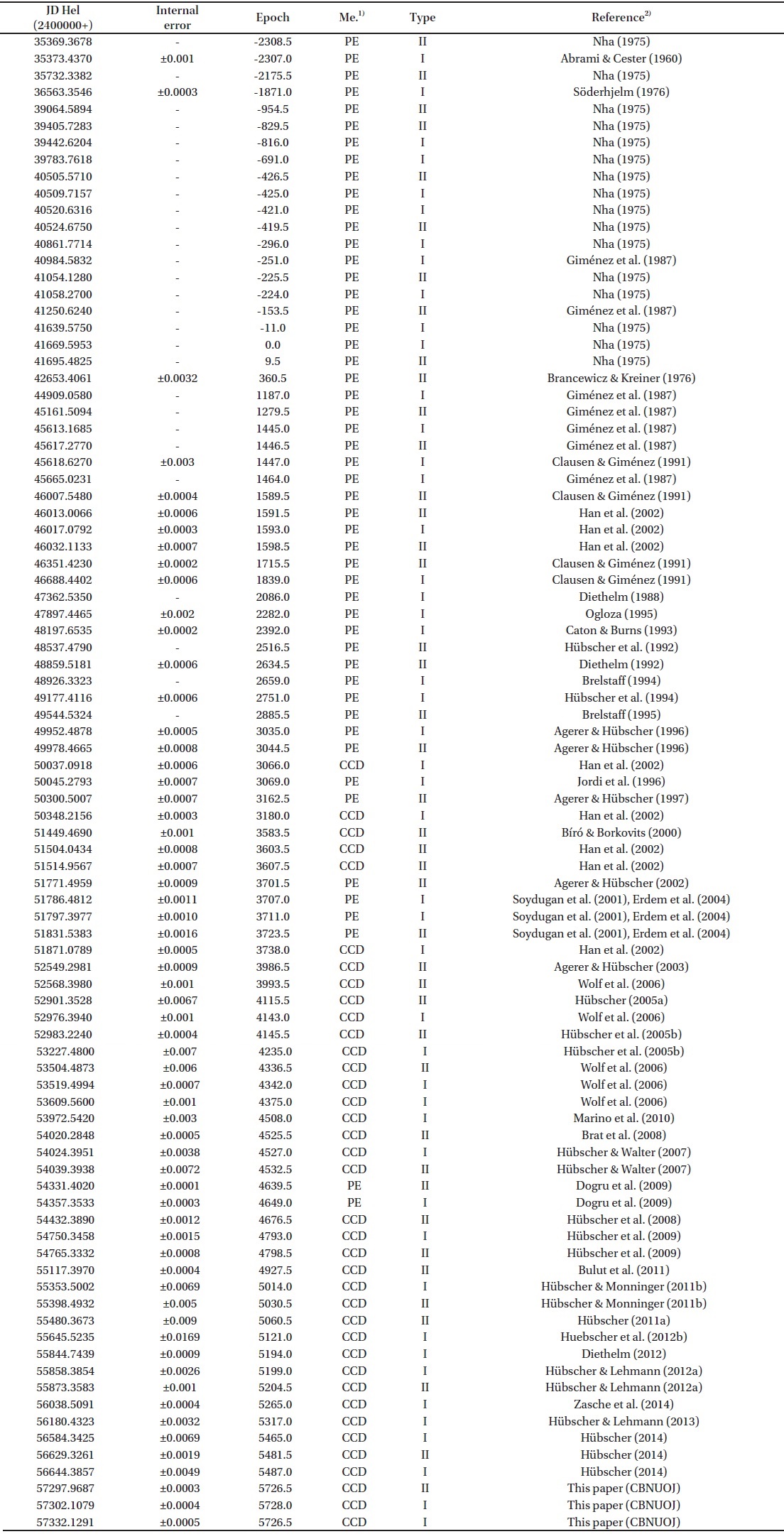
With our new times of minimum lights of CW Cep, we collected all published times of minimum lights from the literature to analyze the apsidal motion of this binary system. Among the available times of minimum lights, the visual and photographic data observed at the early stage of apsidal motion were excluded in this study because those data could increase uncertainty of period variations. Only photoelectric and CCD times of minimum lights were used in our analysis and listed in Table 1, including our timings.
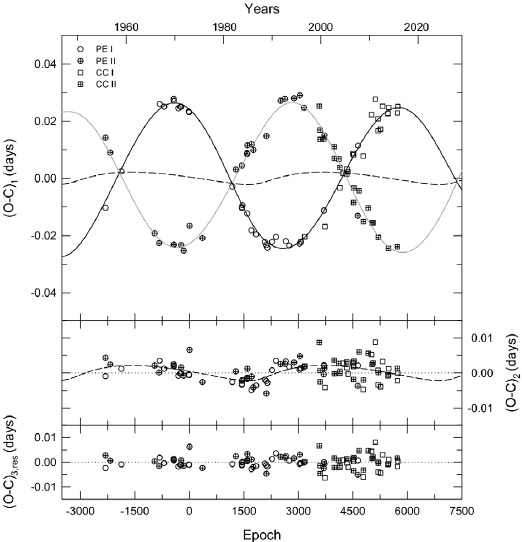
These times of minima were simultaneously analyzed with the apsidal motion plus the light-time effect ephemeris represented by:
where
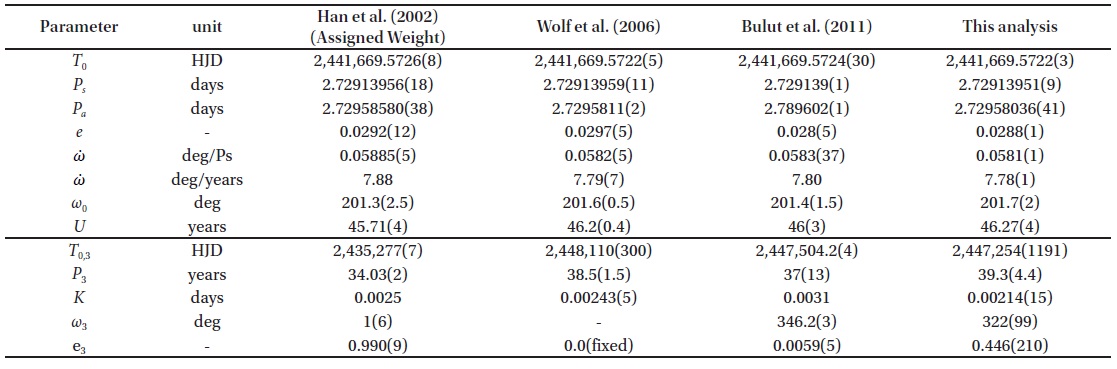
All the timings were fitted to Eq. (1) by using the code (available at http://sirrah.troja.mff.cuni.cz/~zasche/Programs.html) given by Zasche et al. (2009) and Zasche & Wolf (2013). We made small corrections of the code by considering the inclination of the eclipsing pair in it involving up to sixth power of the eccentricity. With the initial values of the apsidal motion and LTE parameter given by Wolf et al. (2006), we improved iteratively the apsidal motion and LTE parameters. the calculation we fixed the inclination of the eclipsing pair as 82.5° derived by Clausen & Giménez (1991) and Han et al. (2002). The final solution was listed in the sixth column of Table 2, together with those et al. (2002), Wolf et al. (2006) and Bulut et al. (2011) for comparison. The resultant O-C diagram was drawn with the linear term of our result in the top of Fig. 1 where the solid continuous curves denote the combination of
[Table 2.] Parameters of the apsidal motion and LTE for CW Cep
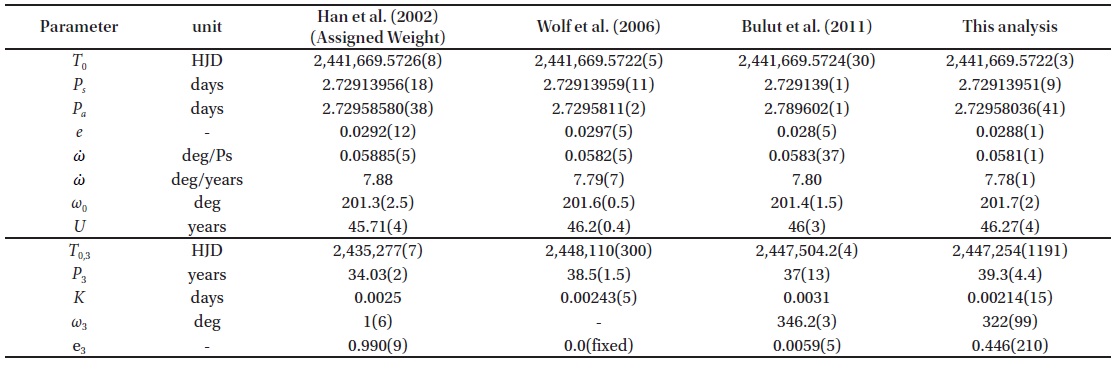
Parameters of the apsidal motion and LTE for CW Cep
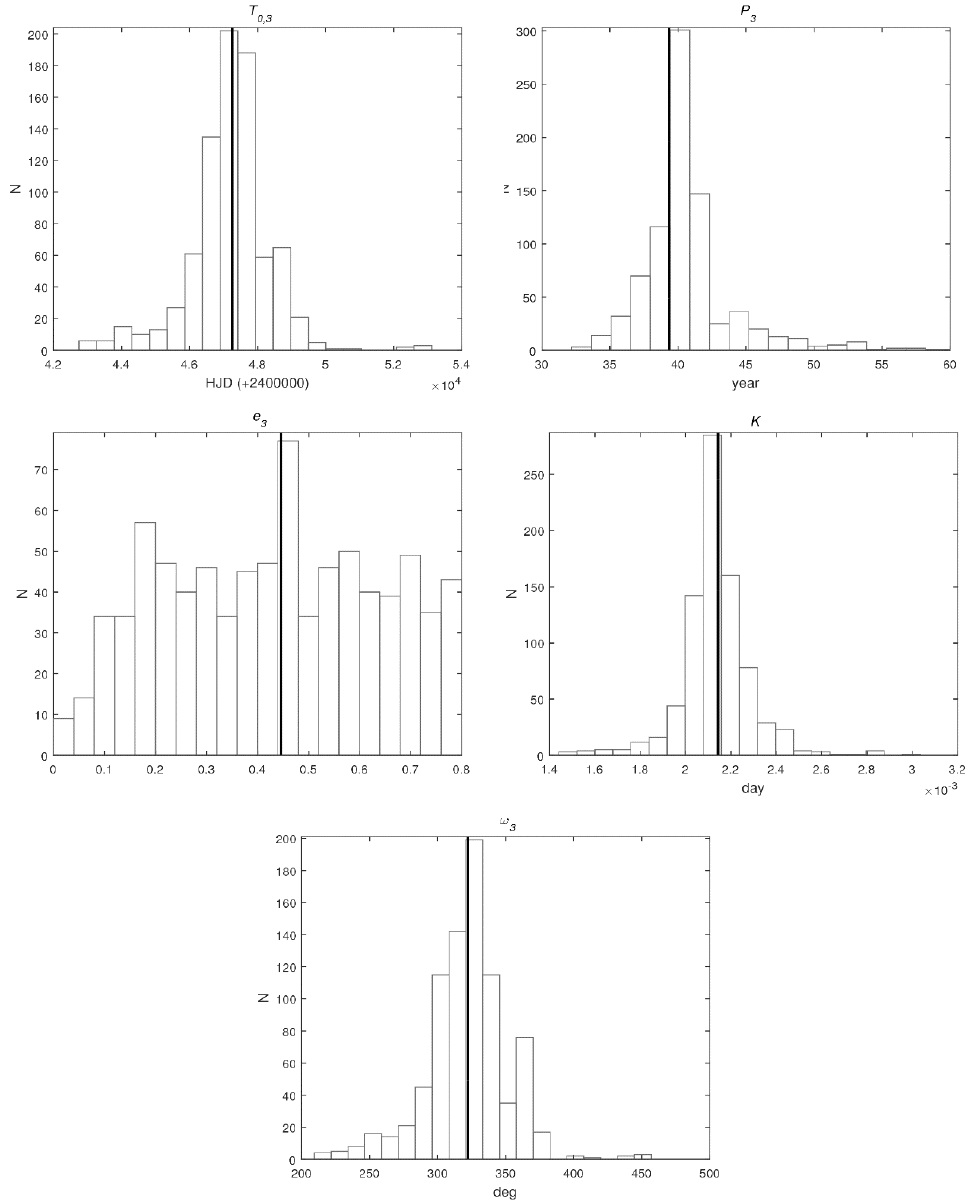
Because the Zasche code we used was based on a differential least-square method Zasche et al. (2009), our solution of Eq. (1) may be a solution with a local minimum rather than a global solution. It would be very necessary to check whether our solution is globally valid for all parameter space. In line with this validity, we subsequently attempted a Monte Carlo simulation to obtain optimized values of the parameters both of the apsidal motion and the LTE orbit as performed by Lee et al. (2015). After 800 simulations all the apsidal motion parameters showed a quick convergence to nearly the same values listed in Table 2, while the LTE parameters show relatively wide variation as shown in the histograms of Fig. 2. Particularly, the distribution of
4. DISCUSSION OF APSIDAL MOTION PERIOD
In this study, the new times of minimum lights were presented by the observations of CBNUOJ, together with the collected times of minimum lights as shown in Table 1. The
The masses and radii of CW Cep by the photometric and spectroscopic parameters suggested by Clausen & Giménez (1991) are