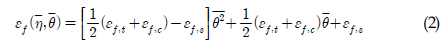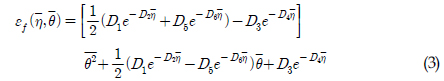본 연구는 본 논문의 제1부에서는 평균 응력 삼축비(Average stress triaxiality)와 평균 정규 로드 파라메터(Average normalized lode parameter)의 이론적 의미에 대하여 고찰하였다. 본 연구는 이전 연구의 확장이므로 이전에 수행된 실험 및 수치 해석적 과정과 제시된 파단 변형률 곡선에 대하여도 고찰하였다(Choung et al., 2011; Choung et al., 2012; Choung et al., 2014a; Choung et al., 2014b; Choung and Nam, 2013). 이전 연구에서 수행되지 못한 낮은 평균 응력 삼축비에서의 실험을 위하여 순수 전단 시편(Pure shear specimen), 전단-인장 시편(Shear-tension specimen), 순수 압축 시편(Pure compression specimen)에 대한 설계/실험 과정을 소개하였다. 순수 전단과 전단-인장 실험의 경우 인장력-스크로크를 실험 결과로 제시하였으며, 순수 압축 실험의 경우 압축력-스트로크(Stroke) 및 공칭 압축 응력-공칭 압축 변형률을 압축 실험의 결과로 제시하였다.

제2부에서는 3차원 파단 변형률 평면을 정식화 하는 과정을 우선적으로 소개할 것이다. 이를 위하여 비선형 유한 요소 해석과정과 결과 처리하는 과정을 소개할 것이다. 이로부터 3차원 파단 변형률 평면을 정식화 하는 과정을 상세히 소개할 것이다. 마지막으로 비대칭 노치를 가지는 시편에 대한 인장 실험을 소개할 것이다. 비대칭 노치 시편의 인장 실험에 대하여 상용 유한 요소 프로그램 Abaqus/Explicit(Simulia, 2008)에 사용자-서브루틴(User-subroutine)을 이식하여 파단을 시뮬레이션 할 것이다. 이로부터 본 연구에서 제시한 3차원 파단 변형률 평면의 유용성을 검증할 것이다.

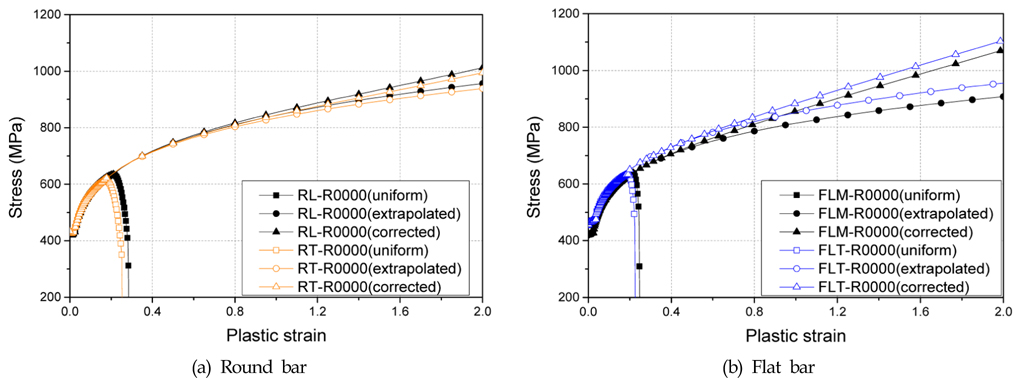
비선형 유한 요소 해석을 위해서 초기 항복 응력에 상응하는 초기 항복 변형률로부터 파단 변형률 구간까지의 유동 응력이 필요하다. 본 논문의 선행 연구(Choung et al., 2011; Coung et al., 2012)에서 수행되었던 환봉형 및 판상형 평활재 인장 실험으로부터 얻은 균일 진 응력(Uniform true stress) 및 균일 진 변형률(Uniform true strain)을 네킹 발생 이전의 유동 응력으로 사용하였다. 반면 균일 진 응력-균일 진 변형률을 식 (1)에 곡선 적합(curve fitting)하여 재료 상수 K(강도 계수, Strength coefficient)와 η(소성 변형률 경화 지수, Plastic strain hardening exponent)을 도출하고, 식 (1)에 재료 상수를 대입하여 네킹 이후의 유동응력을 도출하였다. 이러한 진 응력을 외삽 진 응력(Extraploated true stress)라 칭한다. Choung(2009)에 의하면 외삽 진응력은 큰 소성 변형률에서 유동 응력을 과소 평가하므로 Choung and Nam(2013)이 제시한 방법을 이용하여 외삽 진 응력을 보정하였다. 이를 수정 진 응력(Corrected true stress)이라 칭한다. 이를 Fig. 1에 도식화하여 나타내었다. 수정 진 응력은 수치 해석을 위한 향후 입력 데이터로 사용된다. 즉 네킹 발생 이전과 이후로 구분하여 이전에는 균일 진 응력을 이후에는 수정 진 응력을 모든 노치재(모든 환봉형 및 판상형 노치 시편)의 수치 해석 입력 데이터로 사용하였다.

[Fig. 1] Flow stresses from tensile tests of smooth specimens (Choung and Nam, 2013).

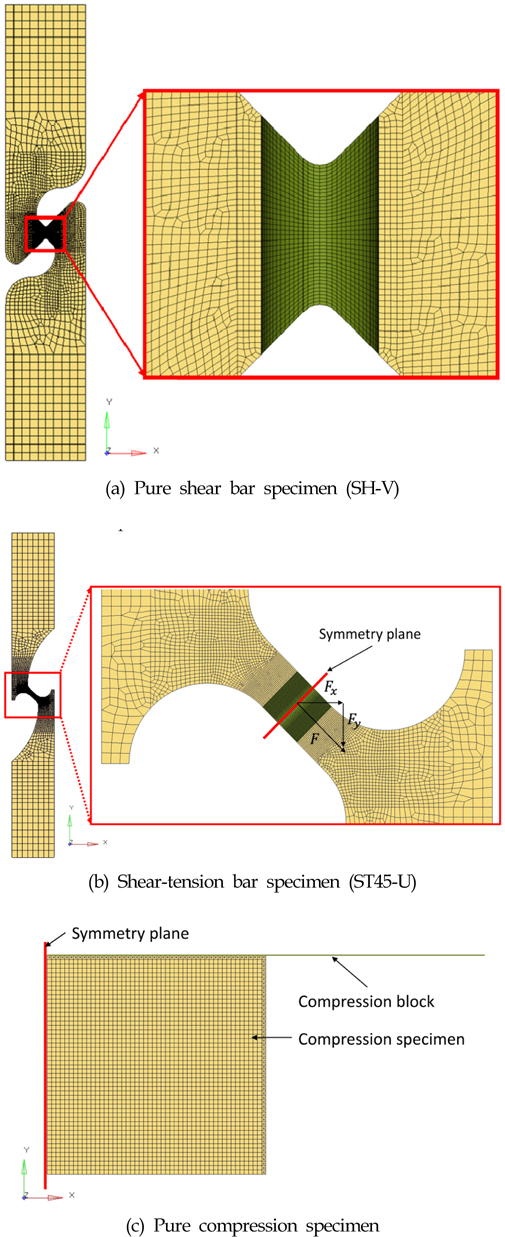
Fig. 2 (a) 및 (b)는 각각 순수 전단, 전단-인장 시편을 유한 요소로 모델링한 형상을 나타낸다. 두께 방향 평면(z축 평면)에 대칭 모델이며, 감차 적분 20절점 고체요소(C3D20R)가 적용되었다. 노치부의 정밀한 모델링을 위하여 l_e/ρ(요소의 길이/노치 반지름)이 0.1이하를 유지하였다. 노치에서 충분히 떨어진 부분에 큰 요소를 배치하고 중간에 요소의 크기 차이를 보정해주기 위한 천이 요소를 배치하여 수치 해석 시간을 단축하였다. 순수 전단 및 전단-인장 시편 모델의 대칭면에 z축 대칭 조건을 부여하였으며, 모델링 상하단을 6자유도 구속하되, 단 상단 절점에 길이 방향(y방향) 강제 변위를 부여하여 인장력을 발생시켰다.

[Fig. 2] Finite element models of specimens.

Fig. 2 (c)에 보인바와 같이 감차 적분 축대칭 요소(CAX4R)를 사용하여 순수 압축 시편을 모델링하였으며, 강체 요소(RAX2)를 가지고 압축력을 전달하기 위한 압축 블록(Compression block)을 모델링하였다. 압축 블록과 순수 압축 시편과의 접촉면에서의 마찰 계수(Friction coefficient)를 알수 없기 때문에 마찰 계수를 시행착오적으로 변경하면서 수치 해석을 수행하고 압축 하중-압축 스트로크 선도를 실험 결과와 비교하여 마찰 계수를 결정하였다. 결정된 정 마찰 계수(Static friction coefficient)는 0.01이었으며, 모든 순수 압축 수치해석에 동일하게 적용되었다. 금속 간의 정 마찰 계수는 대략 0.7을 상회하는 것으로 알려져 있지만, 본 연구에서는 윤활유을 충분하게 사용하여 매우 작은 정 마찰 계수가 얻어진 것으로 분석된다. 압축 요소는 시편 길이 방향(y축 평면)에 대칭 모델이며, 강체 요소에 강제 변위를 부여하여 압축 하중을 구현하였다. 시편 모델링을 위하여 Altair/HyperMesh(Altair, 2013)를 사용했으며, Abaqus/Standard(Simulia, 2008)을 이용하여 유한 요소해석을 실시하였다.

순수 전단 시편은 소성 변형 중에도 x평면에 거의 대칭으로 간주될 수 있으므로, 소성 변형 중의 x방향 힘(F_x)이 발생하지 않는다고 간주될 수 있다. 그러나 전단-인장 시편의 경우 탄성 변형부터 소성 변형까지 x방향 및 y방향 힘(F_x 및 F_y)이 작용한다. 즉 전단-인장 시편의 경우 두방향 성분의 변형이 동시에 발생하기 때문에 수치해석에서 이를 정확히 구현하여야만 신뢰성 있는 수치해석으로 간주될 수 있다.

Fig. 2 (b)에서 대칭면의 상부에 존재하는 시편만을 고려하면, F_x를 경험하므로 시편의 대칭면 상부는 지그에 고정된 외팔보와 같다. 이 외팔보의 x방향 처짐은 외팔보의 길이에 따라 변동적 일 것이다. 실험에서 이 외팔보의 유효 길이를 변동시키는 원인은 다음과 같이 추정할 수 있다. 시편의 중앙부보다는 압착부 종단(시편의 양끝단)에 큰 유압이 가해지며, 이는 외팔보의 유효 길이가 길어질 수 있음을 의미한다. 실제 실험이 종료된 시편으로부터 시편의 양 끝단에 훨씬 선명한 압착 흔적을 확인할 수 있었으며, 시편의 중앙부에 가까운 압착부는 압착의 흔적이 거의 없는 경우도 관찰할 수 있었다. 이러한 이유로 압착부가 지그에 의하여 완전히 고정되었다고 가정하여 수행한 수치 해석 결과는 하중 측면에서 실험과 거의 일치하였지만, 변위(스크로크) 측면에서는 실험의 변위가 크게 나타남을 목격할 수 있었다.

본 연구에서는 이러한 문제를 해결하기 위하여 실험 후 시편의 외관 검사를 통하여 UTM(universal testing machine) 지그의 유효 압착 지점을 육안으로 확인한 결과 Fig. 3과 같이 길이 방향 중앙부에 가까울 수록 압착이 유효하지 않음을 확인할 수 있었다. 따라서 압착부가 선명한 지점까지를 모델의 초기 길이로 설정하고, 실험 결과와 일치할때까지 전단-인장 시편의 모델 길이를 증가시키면서(유효 압착 길이를 감소시키면서) 수치 해석 결과를 실험 결과와 동기화하는 작업을 수행하였다.

[Fig. 3] Effective grip marks on specimen ST15-NV

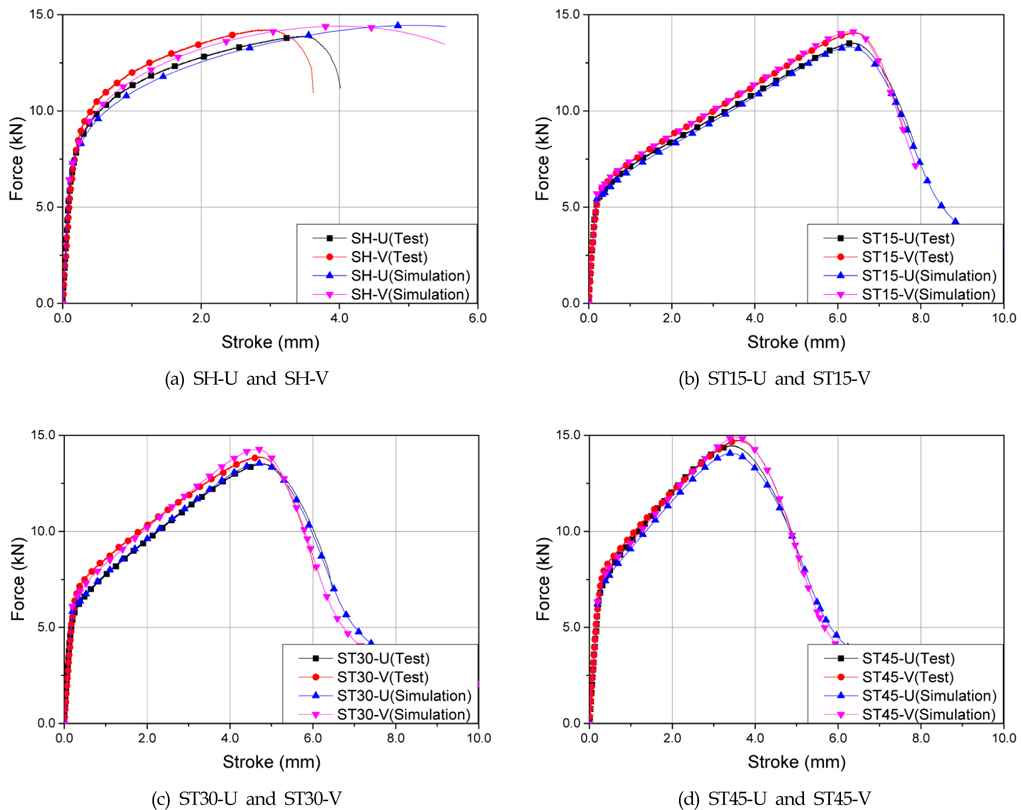
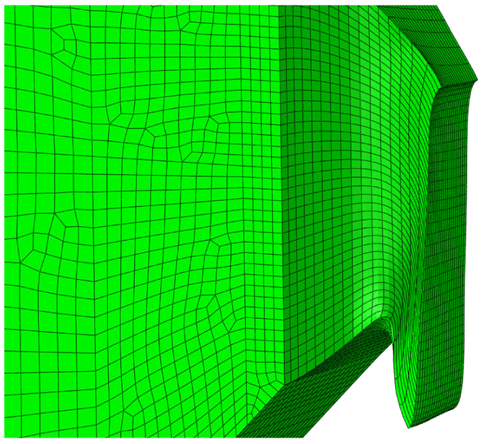
순수 전단 및 전단-인장 시편에 대한 실험 및 수치해석으로부터 얻어진 인장력-스트로크 곡선을 Fig. 4에 비교하여 나타내었다. 전단-인장 실험 결과는 탄성 변형부터 파단에 이르기까지 전체 변형에 걸쳐 수치 해석 결과와 매우 잘 일치한다(Fig. 4 (b), (c), (d)참조). 반면, 순수 전단(SH-U, SH-V) 수치 해석 결과는 파단이 발생하기 이전까지 실험과 비교적 일치하지만, 최대 하중 이후부터 실험과 많은 차이를 보이고 있다. 즉 순수 전단 수치 해석으로부터 하중의 감소를 얻을 수 없었다(Fig. 4 (a) 참조). 수치 해석에서는 파단이 발생해야 하는 노치부에 전단 응력이 지배적이었기 때문에 노치부 요소도 전단 변형만 했으며, 단면적의 변화가 없었다. 즉 노치부 요소에 체적 잠김 (Volume locking)이 발생하여 하중의 감소가 발생하지 않은 것으로 추정된다. Fig. 5는 전단 시편의 대칭면에 대한 변형 후 형상을 나타내며, 체적 잠김이 발생하였음을 육안으로 확인할 수 있다.

[Fig. 4] Comparison of simulated tensile force versus stroke data with test ones for pure shear and shear-tension tests.

[Fig. 5] Volume locking at the symmetric section of pure shear specimen.

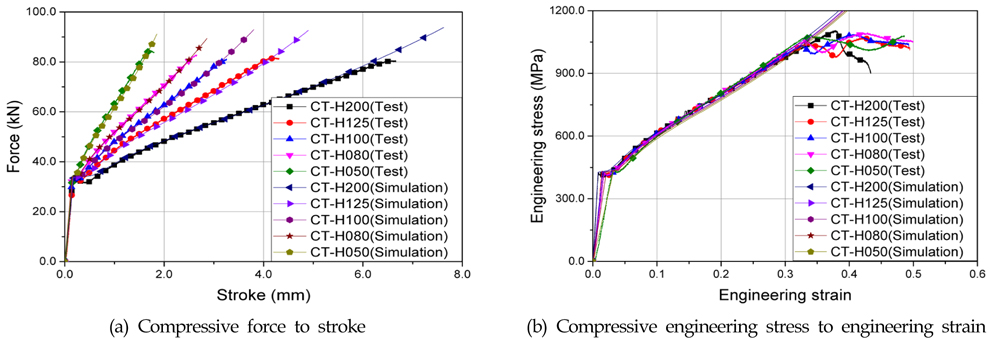
압축 실험 시뮬레이션으로부터 얻은 압축 하중-압축 스트로크 선도와 응력-공칭 변형률 선도는 실험 결과와 매우 일치하는 것으로 보여진다(Fig. 6 참조). 수치 해석 역시 시편의 길이가 길어짐에 따라 전체적인 유동 응력이 낮아 짐을 확인 할 수 있다. 모든 압축 실험의 실험과 수치해석 결과가 정확히 일치하고 있다.

[Fig. 6] Comparison of simulated results with test ones for compression tests.

Bai and Wierbicki(2008)은 평균 응력 삼축비와 평균 정규 로드 파라메터를 변수로 연성 재료의 파단 변형률 평면을 제시했다(식 (2) 참조). 여기서 ε_f,t, ε_f,s , ε_f,c는 각각 인장, 전단, 압축에 기인한 파단 변형률의 단위항을 의미한다. 각 성분에 기인한 파단 변형률은 평균 응력 삼축비의 함수이며, 2개의 재료 상수를 가진다. 즉 인장에 관한 재료 상수는 D₁ 및 D₂ , 전단에 관한 재료 상수는 D₃ 및 D₄ , 압축에 관한 재료 상수는 D₅ 및 D₆이다. 최종적으로, 각 단위항의 조합을 계수항으로 가지는 평균 정규 로드 파라메터의 2차식으로 파단 변형률을 표현하였다(식 (3) 참조).

재료 상수는 실험 결과와의 회귀 분석을 통하여 결정이 가능한다. 3차원 회귀 분석을 통하여 결정된 계수는 D₁=3.32, D₂=1.232,D₃=1.472, D₄=0.0673, D₅=0.0702, D₆=-1.086이며, 수정 결정 계수(Adjusted R-square coefficient)는 95.6%로서 실험 결과와 상당히 높은 상관 관계를 보여주었다.

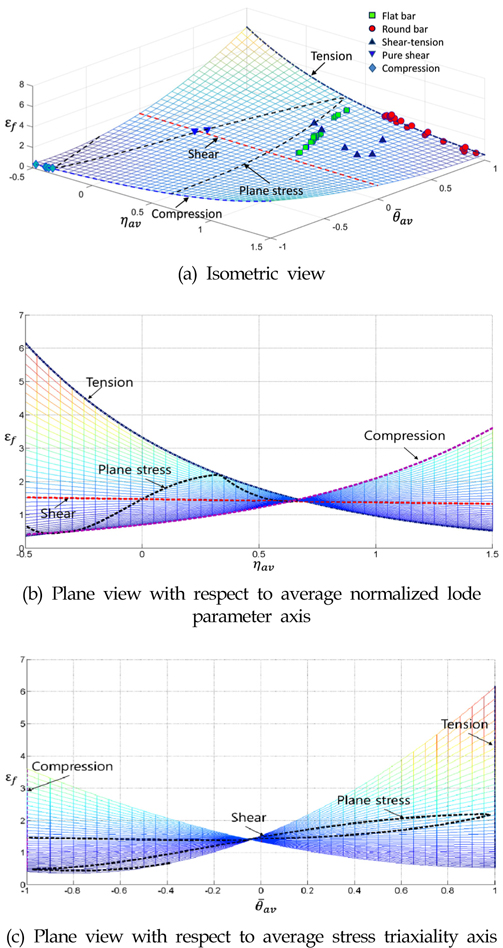
식 (3)을 이용하여 3차원으로 나타낸 파단 변형률 평면은 Fig. 7과 같다. 전단 응력만 작용하는 경우 파단 변형률은 거의 상수로 간주됨을 Fig. 7 (a) 또는 (c)로부터 알수 있다. 즉 전단 응력만 작용한다면, 평균 응력 삼축비가 파단 변형률에 거의 영향을 미치지 않는다는 의미이다. 반면 인장 응력이 지배적일 경우(=1.0), 파단 변형률은 평균 응력 삼축비의 영향을 가장 크게 받는 것으로 나타났다. 물론 압축 응력이 지배적일 경우(=-1.0)에도 평균 응력 삼축비는 파단 변형률에 상당한 영향을 미침을 알 수 있다. 평면 응력 상태를 유지한다면, 파단 변형률은 평균 응력 삼축비와 평균 로드 파라메터에 모두 영향을 받는다.

[Fig. 7] Three dimensional fracture strain surface.

개발된 파단 변형률 평면의 유용성을 검증하기 위해서는 인장 응력, 전단 응력, 압축 응력이 지배적인 실험과 3개 응력 성분의 조합에 따른 실험이 필요하다. 이러한 실험은 방대한 비용과 시간이 요구되므로, 본 논문에서는 Fig. 8에 보인 것과 같이 노치에서의 인장 응력이 지배적일 것으로 예측되는 비대칭 노치 시편을 설계/가공하였다. 따라서 본 논문에서의 파단 변형률 평면의 검증은 인장 응력에 기인한 파단에 국한된다.

[Fig. 8] Asymmetric notch bar specimens.

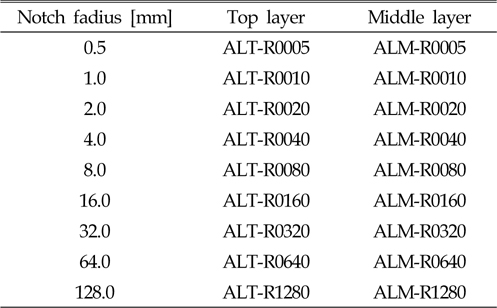
시편의 기본 형상은 Choung and Nam(2013)에서 적용한 판상형과 동일하지만, 폭방향으로 한쪽에만 노치가 가공되었다. 시편은 모재 두께의 상층과 중층에서 강재 롤링 방향으로 가공되었다. 시편의 명칭은 Table 4에 나타나 있다. 실험 결과는 수치 해석 결과와 비교하여 이후 절에서 나타내었다. 실험은 MTS사의 25톤급 UTM을 이용하여 실시되었으며, 표점 거리 50mm의 신률계를 사용하여 표점간의 변위를 계측하였다.

[Table 1] Labels of asymmetric bar specimens.

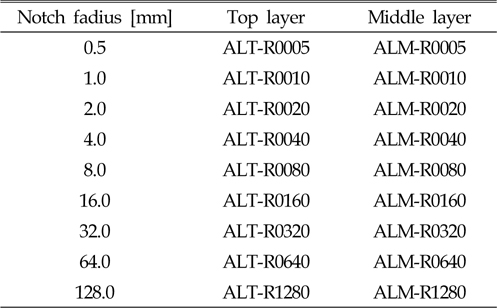
Labels of asymmetric bar specimens.

시뮬레이션 도중 요소의 파단을 구현하기 위하여 상용 유한 요소 해석 코드인 Abaqus/Explicit(Simulia, 2008)을 사용하였다. Abaqus/Explicit은 변형률 속도, 응력 삼축비, 온도를 기본 변수로 파단 변형률을 정의할 수 있으며, 평균 응력 삼축비와 평균 로드 파라메터가 본 연구에서 사용하고자 하는 변수이므로 Abaqus/Explicit의 사용자 정의 변수 VUSDFLD(User subroutine to redefine field variables)를 새롭게 정의할 필요가 있다. 본 연구에서는 두개의 사용자 정의 파라메터에 따른 파단 변형률을 표로 이산화하여 유한 요소 모델 파일에 입력하였다.

평균 응력 삼축비와 평균 로드 파라메터를 계산하기 위한 사용자-서브루틴의 개발이 필요하다. 공학용 컴파일러인 포트란(Fortran)을 통하여 유한 요소 모델의 모든 요소의 적분점에서 응력 성분과 및 변형률 성분을 실시간으로 도출하고 평균 응력 삼축비와 평균 로드 파라메터를 계산하여 유한 요소 모델로 전달하는 사용자-서브루틴을 개발하였다. 파단 파라메터를 전달받은 Abaqus/Explicit은 특정 요소의 적분점이 변형률 평면을 초과했는지 판단하고 초과했다면 특정 요소는 파단된 것으로 간주한다.

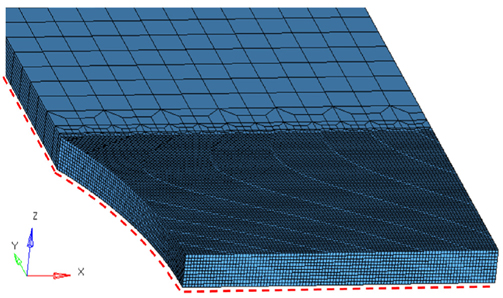
Fig. 9는 본 연구에서 개발한 3차원 파단 변형률 평면에 대한 검증을 위한 비대칭 노치 시편의 유한 요소 모델이다. 비대칭 노치 시편의 유한 요소 모델은 판상형 시편의 수치 해석 모델(Choung and Nam, 2013)과 동일한 요소를 사용하였으며, 동일한 요소 크기 제약을 가진다. 단, Choung and Nam(2013)은 x 평면, y평면, z평면에 관한 각 대칭 조건을 적용하여 1/8 대칭 유한 요소 모델을 사용하였지만, 비대칭 노치 시편의 경우 y평면에 관하여 비대칭이므로 1/4 대칭 유한 요소 모델을 사용하였다. 본 모델에 적용된 하중 조건과 경계 조건은 Choung and Nam(2013)과 거의 유사하며, 시편 중앙부 최소 횡단면의 x축을 따라 y축 대칭 조건, 두께 방향 대칭면에 z축 대칭 조건을 부여하였다. 수치 해석에 사용된 유동 응력은 Fig. 1 (b)의 균일 진응력(네킹 발생 이전)과 수정 진 응력(네킹 발생 이후)이었다.

[Fig. 9] Finite element models of an asymmetry specimen with applied boundary conditions.

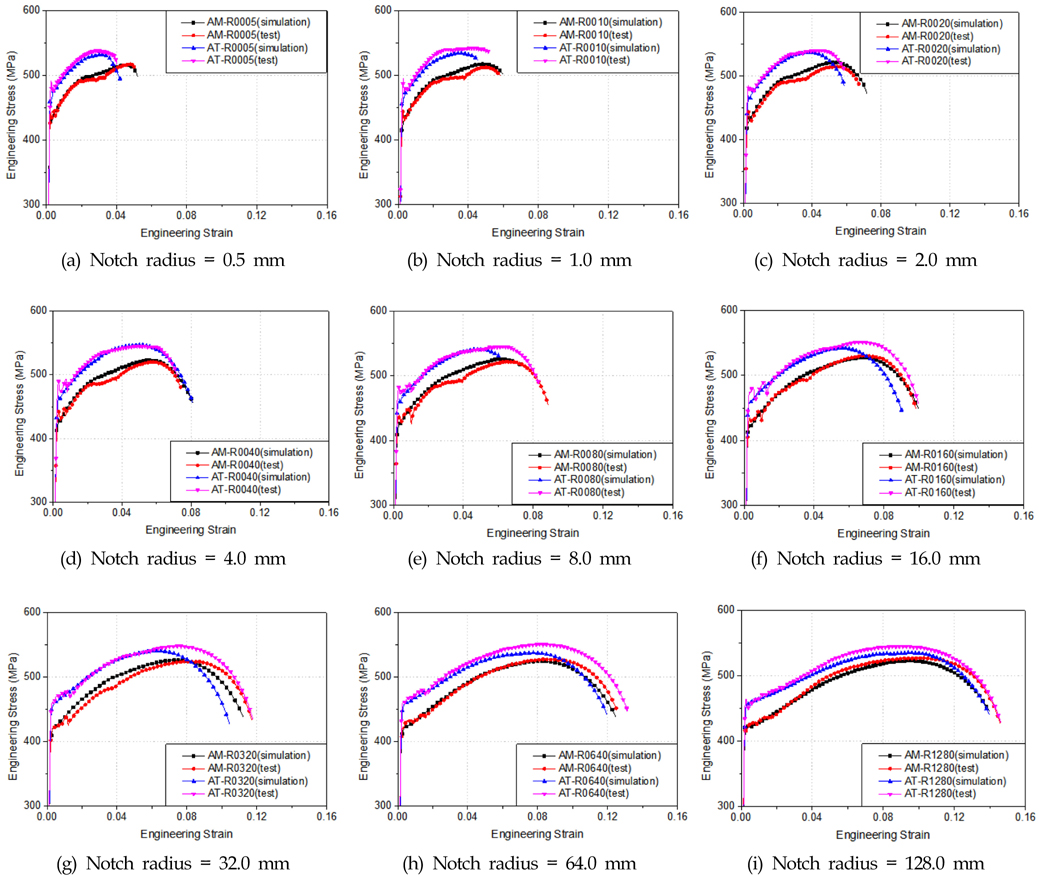
Fig. 10는 사용자 정의 서브루틴을 Abaqus/Explicit에 이식하여 얻은 수치 해석 결과(공칭 응력-공칭 변형률 선도)를 실험결과와 비교하여 나타낸 그래프이다. 실험에서 얻은 공칭 응력-공칭 변형률 선도의 경우 소성 변형하는 도중에 공칭 응력의 불연속부가 존재함을 Fig. 10로부터 확인할 수 있다. 응력의 불연속은 노치가 작을수록 확연하게 나타나는 경향이 있다. 작은 노치의 경우 거의 초기 균열과 같은 역할을 하며 인장력에 의하여 균열이 처음 진전할때 하중의 감소로 인하여 발생하는 현상으로 추정된다.

[Fig. 10] Comparison of engineering stress versus strain curves of asymmetric notch specimens.

Fig. 10로부터 수치 해석에 의한 파단 시점은 실험에서의 파단 시점을 비교적 잘 예측한다고 판단된다. 노치가 작을수록 예측의 정확성은 높을 것으로 보여진다. 그러나 노치가 큰 시편의 경우 파단 시점의 편차는 물론이고, 소성 변형 프로세스에서 무시하지 못할 편차를 보인다. 이는 본 연구에서 사용한 수정 진 응력의 부정확성에 기인한 것으로 추정된다. 즉 외삽 진 응력(Extraploated true stress)으로부터 수정 진 응력(Corrected true stress)을 예측하여 사용하였지만, 큰 소성 변형률에서의 유동 응력이 아직도 과소 평가된 결과로 사료된다. 따라서 수치 해석의 정량성을 담보하기 위해서는 유동 응력의 정확성을 향상하기 위한 연구가 필요할 것으로 사료된다.

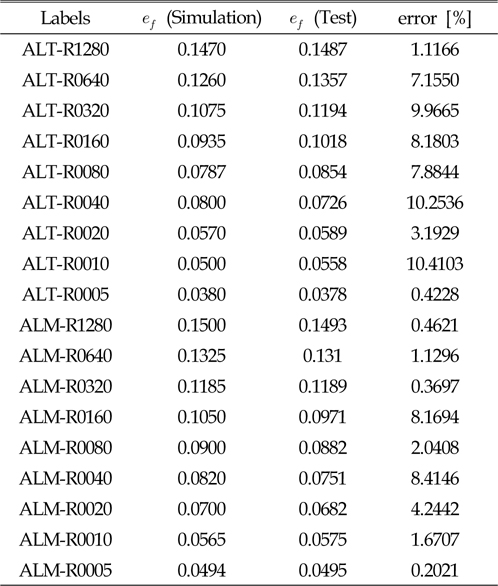
실험과 수치 해석에서 얻은 공칭 파단 변형률을 비교하여 Table 2에 나타내었다. 최대 오차는 10% 내외이며, 오차의 평균과 표준 편차는 각각 4.9% 및 4.1%이다. 본 논문에서 제시한 3차원 파단 변형률 평면은 인장 하중에 대하여 비교적 정확한 파단을 예측하고 있다고 판단된다.

[Table 2] Comparison of engineering fracture strains for asymmetric notch specimens.

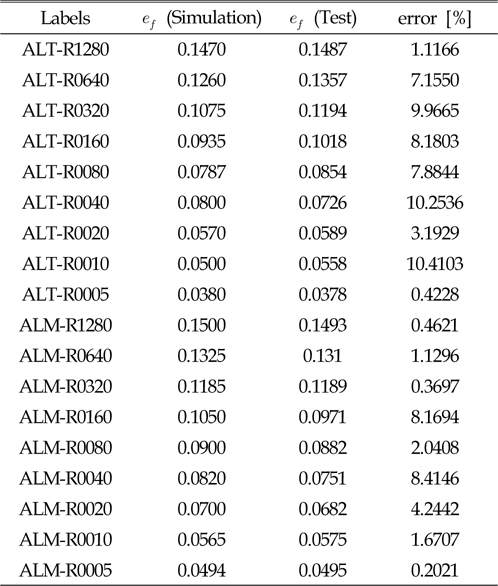
Comparison of engineering fracture strains for asymmetric notch specimens.

본 논문의 제1부에서는 파단의 주요 파라메터인 평균 응력 삼축비와 평균 정규 로드 파라메터의 이론적 배경과 3차원 파단 변형률 평면을 개발하기 위한 선행 연구와 새로이 수행된 실험 연구 내용이 소개되었다. 선행 연구(Choung et al., 2011; Coung et al., 2012)에서는 환봉형 및 판상형 시편의 인장 실험 결과를 이용하여 외삽 진 응력 및 수정 진 응력을 도출하는 과정을 제시하였다. 새로이 수행된 실험은 순수 전단 실험, 전단-인장 실험, 순수 압축 실험이었다.

본 논문의 제2부에서는 1부에서 수행된 실험에 대한 수치 해석을 상세히 소개하였으며, 이 결과를 토대로 3차원 파단 변형률 평면의 정식화가 수행되다. 또한 파단 변형률의 검증을 위한 추가 실험 및 수치 해석 과정이 소개되었다.

전단-인장 및 순수 압축 실험의 시뮬레이션은 실험과 거의 동일한 수준의 하중-스트로크 선도를 예측하였다. 그러나 순수 전단 실험의 시뮬레이션의 경우 하중의 감소가 발생하지 않고 지속적으로 인장 하중이 증가하는 현상이 발생하였으며, 이는 순수 전단 시편 노치부 요소가 전단 변형할때의 체적 잠김에 기인한 것으로 추정되었다. 파단 발생 지점과 파단 발생 시점에서의 평균 응력 삼축비, 평균 정규 로드 파라메터, 그리고 등가 소성 변형률을 추출하여 파단 변형률의 정식화에 사용하였다.

Bai and Wierzbicki(2008)가 제시한 평균 정규 로드 파라메터에 관한 2차 다항식을 파단 변형률 평면의 기본 수식으로 활용하여, 인장 응력, 전단 등력, 압축 응력에 대한 각각의 재료 상수를 2개씩 도출하였다. 도출된 3차원 파단 변형률 평면은 실험 결과와 상당히 밀접한 상관 관계를 가지는 것으로 파악되었다. 전단 응력만 작용하는 경우 평균 응력 삼축비의 영향이 거의 존재하지 않음을 확인하였으며, 인장 응력 또는 압축 응력이 지배적일 경우 평균 응력 삼축비의 영향을 무시할 수 없다는 점을 파단 변형률 평면으로부터 파악할수 있었다.

파단 변형률 평면의 유효성을 검증하기 위하여 비대칭 노치를 가지는 시편을 설계/제작하여 인장 실험을 실시하였다. 또한 평균 응력 삼축비와 평균 정규 로드 파라메터는 상용 유한 요소 해석 코드의 파단 변수로 사용할 수 없기 때문에 이 파라메터를 수치 해석에 도입하기 위하여 사용자-서브루틴을 개발하였다. 사용자-서브루틴을 적용한 비대칭 노치 시편의 수치 해석을 수행한 결과 실험 결과와 잘 일치하는 결과를 얻었고, 3차원 파단 변형률 평면의 유효성을 검증하였다.

향후 개선 사항으로서, 순수 전단 시뮬레이션의 하중 감소를 구현하기 위하여 고차 형상 함수 요소나 하이브리드 요소 등의 사용을 검토할 필요가 있다. 또한 선행 연구(Choung et al., 2011; Coung et al., 2012; Choung and Nam, 2013)에서 큰 노치를 가지는 대칭 시편의 경우 수치 해석이 실험과 비교적 큰 차이를 보였던 것처럼 본 논문에서 제시하는 비대칭 노치 시편의 시뮬레이션에서도 큰 노치를 가지는 시편에서의 편차가 큰 것을 확인하였다. 이는 수정 진응력이 외삽 진응력의 기울기를 증가시키는 역할을 하였음에도 여전히 소재의 유동 응력을 과소 평가해서 발생하는 문제이므로 이에 대한 향후 연구가 필요하다. 전단 응력이 지배적인 시편과 압축 응력이 지배적인 시편에 대한 추가적인 실험을 통하여 파단 변형률 평면의 유효성을 넓은 범위의 파단 파라메터에 대하여 검증할 필요가 있다. 본 논문의 제1부에서 기술한 바와 같이 응력의 비비례성(Nonproportionality)이 파단 변형률 평면의 형성에 영향을 줄수 있으므로 향후 이에 대한 엄밀한 연구가 요구된다.