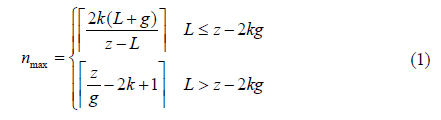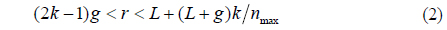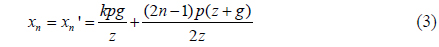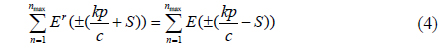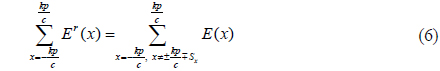Integral imaging is a technique capable of recording and reconstructing a 3D object with a 2D image array having different perspectives of a 3D object. It has been regarded as the most promising technique because of its full parallax, continuous viewing, and full-color images [1-4]. However, this technique suffers from some problems such as limited image resolution [5-7], narrow viewing angle, and small image depth.

To overcome the disadvantage of limited image resolution, many modified methods have been proposed [8-12]. A curved computational integral imaging reconstruction technique has been proposed in [11, 12], which is an outstanding method to enhance the resolution of three-dimensional object images. However, the utility of the virtual large-aperture lens may introduce some distortions because of the curving effect in this method.

In this paper, to improve the resolution of the computationally reconstructed 3D images, we propose a novel approach for the resolution enhanced pickup process by using boundary folding mirrors. In the proposed method, 3D objects are picked up by a lenslet array with boundary folding mirrors as a combined elemental image array (CEIA), which can record more perspective information than the regular elemental image array (REIA) because of the specular reflection effect. The recorded CEIA is computationally synthesized into a REIA by using a ray tracing method. Finally, by using the REIA, the resolution-enhanced 3D images could be computationally reconstructed in the proposed method. To show the feasibility of the proposed method, preliminary experiments are performed.

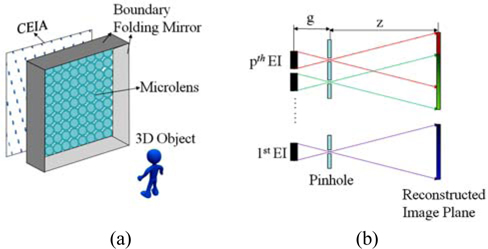
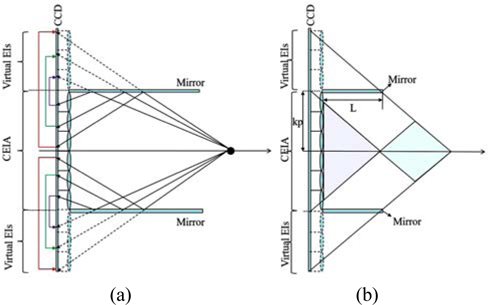
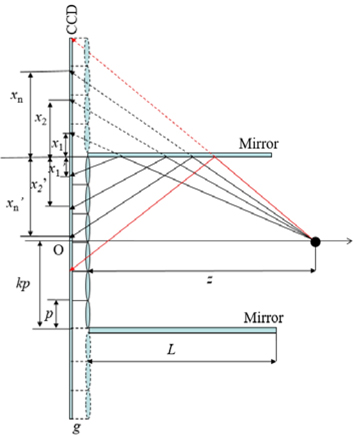
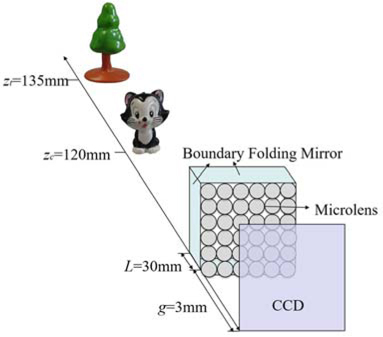
Figure 1(a) shows the pickup system which uses a lenslet array and boundary folding mirrors to capture 3D objects [13]. Compared with conventional integral imaging system, the pickup systems can record both direct light information from the 3D objects and reflected light information from the boundary folding mirrors. Here, it is worth noting that the reflected information of the CEIA contains extra perspective information from the 3D objects. In order to computationally reconstruct resolution enhanced 3D images, the CEIA is necessary to generate a REIA, especially the reflected information of the CEIA needs to reorganize virtual elemental images (EIs) as shown in Fig. 2 (a). The lenslet array denoted by dashed lines is a virtual lenslet array mirrored by boundary folding mirrors. The red, green and purple arrowed lines denote the mapping directions.

Before synthesizing the REIA, the maximum number of additional microlenses n_max should be determined. With a size 2k×2k lenslet array, there exist two restrictions conditions on the length of boundary folding mirrors and the pitch size of microlenses:

where L is the length of the boundary mirror, ⌈ · ⌉ is the rounding operator. Then, to measure the best pickup area for all the microlenses including the additional ones, each elemental image must contain reflected information as shown in the green area of Fig. 2(b). Therefore, the best pickup area r along the z axis can be calculated as:

If the 3D objects are located in the purple area of Fig. 2(b), the reflected information cannot be recorded through the additional microlenses. If the 3D objects are located out of the green and purple areas of Fig. 2(b), some but not all of the additional microlenses can be exploited for recording reflected information

Next, we consider only the one dimensional case to simplify the mapping relationship between the reflected information of the CEIA and the virtual EIs. Suppose that an object point is located at a longitudinal distance z away from the lenslet array, and the gap between the sensor and the lenslet array is g as shown in Fig. 3. Based on the specular reflection, the distance x_n’ between the reflection point in CEIA and the boundary mirror is equal to the distance x_n between reflected object point in virtual EIs and the boundary mirror:

Then, we can get the mapping relationship between the reflected information of the CEIA E and the REIA E^r :

where n is the number of additional microlenses, c is the pixel size. The remaining information of the CEIA except for the reflected information can be directly mapped into the REIA:

By using the Eq. (4) and Eq. (6), the REIA E^r can be obtained with the size of (2k + n)p × (2k + n)p. Compared with the conventional integral imaging method, the visual quality of the reconstructed 3D images will be improved by using the proposed method, because the reflected elemental images can provide additional 3D information.

In the computational integral imaging reconstruction process, a high resolution 3D scene can be reconstructed based on the back-projection model. The 3D image reconstructed at (x, y, z) is the summation of all the inversely mapped REIA:

where R(x, y, z) denotes the reconstructed 3D images, s_x and s_y are the sizes of elemental image , respectively, M is the magnification factor which is defined as M = z/g.

To demonstrate the feasibility of the proposed method, we performed some experiments with 3D objects composed of a cat and a tree as shown in Fig. 4.

In the experimental setup, the gap between the imaging sensor and the lenslet array was set to 3 mm, which is equal to the focal length of the microlens. The 3D objects cat and tree are located 120 mm and 135 mm from the lenslet array, and the length of the mirror is 30 mm. Here, the lenslet array is composed of 30×30 microlenses, and each microlens has a uniform size of 1.05 mm ×1.05 mm with focal length of 3 mm. Figure 5(a) shows a captured CEIA, in which the pixel number of each EI is 50×50. There exists mirror reflected information of a 3D object in the CEIA because of the boundary folding mirrors, as shown in the red block of Fig. 5(a). As we discussed earlier, to synthesize the REIA, the 6 additional lenses are determined by using Eq. (3). Then, the REIA is synthesized by using the reflected information of CEIA, in which the REIA contains more 3D perspectives, as shown in the green block of Fig. 5(b).

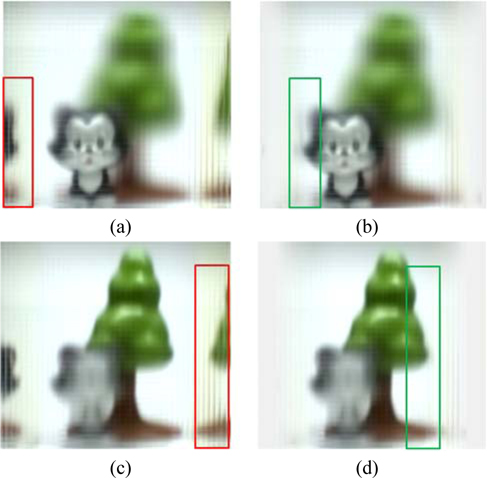
In the experimental results, we utilized the original captured CEIA and synthesized REIA to reconstruct the 3D images. The 3D objects cat and tree are reconstructed at distances 120 mm and 135 mm, respectively. Figure 6(a) and 6(c) are the computationally reconstructed 3D images by using the CEIA, where the reconstructed images are focused on the cat and the tree, respectively. The region of the red block is the reflected 3D information. Figure 6(b) and 6(d) are the computationally reconstructed 3D images by using the REIA, where the reconstructed images are focused on the cat and the tree, respectively. Compared with the region in the red block of Fig. 6(a) and 6(c), the reflected light information is overlapped on the direct light information as shown in green block of Fig. 6(b) and 6(d). This can significantly improve the quality of the computationally reconstructed 3D images by using a REIA. In addition, the zoomed-in region of the Figs. 7(a) and 7(b) confirm that the visual quality of the computationally reconstructed 3D images by using the REIA is sharper than by using the CEIA. From the experimental results, we confirm the feasibility of the proposed method.

In conclusion, we have presented a resolution-enhanced computational 3D reconstruction method by using boundary folding mirrors in an integral imaging system. In the proposed method, a CEIA that contains extra reflected perspective information is picked up firstly by using a lenslet array combined with boundary folding mirrors. The generated REIA is synthesized from the captured CEIA, in which the REIA is used to reconstruct resolution-enhanced 3D images. The experimental results confirmed the feasibility of the proposed system.