선박이나 해양구조물의 건조과정에서 러그는 블록의 인양과 반전(turn over)에 사용된다. 최근 건조공정의 효율성을 제고하기 위해 선박이나 해양구조물의 블록이 대형화 되어 가고 있고 이에 따라 사용되는 러그의 수가 많이 증가하고 있다. 러그는 소모성부재이기는 하지만 재료비 절감 측면에서 재활용, 블록의 인양과 반전에 필요한 최적 위치의 선정과 최적의 수량 결정 등에 대한 중요성이 부각되고 있다 (Ham, 2000; Kim, 2003; Ku, et al., 2012). 한편으로는 블록의 이동 등에 사용되는 많은 수의 러그를 제작, 설치, 해체 등의 비용이 많이 소요되므로, 충분한 강도를 지니면서 단순화, 경량화를 통해 원가 절감을 해야만 하는 현실이다. 또한 리프팅 러그가 파단 되었을 때에 안전과 공정상에 있어서 큰 문제가 발생하기 때문에 설계에 있어 각별한 주의가 요구된다 (Kim, 2006; Seo, et al., 2011).
이러한 배경에 의거하여 본 연구에서는 먼저 본 연구의 해석 과정의 타당성을 검토하기 위해 수치해석 결과를 참고문헌의 실험결과와 비교하였다 (Heo & Lee, 2014; Lee & Heo, 2013). 본 연구는 최종 강도를 기준으로 한 러그 구조의 최적설계를 목표로 설전하였으며, 대상 러그는 현재 블록의 인양과 반전에 널리 사용하는 T형 러그(T type lug)로서 1회용이 아닌 재활용이 가능한 모델을 선정하였다. 용량은 20, 30, 40 그리고 50 ton으로서 네 가지 모델이다. 최종 강도를 추정하기 위해 비선형 구조해석을 위하여 상용 유한요소해석프로그램인 Abaqus를 사용하였다 (Simulia, 2013)을 사용하였다. 본 연구를 위한 선행 연구 결과 (Heo & Lee, 2014, Lee & Heo, 2013; Lee, et al., 2014)에 의하면 러그 구조의 하중-변위 곡선 형태가 최종강도를 용이하게 구할 수 있는 형태가 아니어서, 여기에서는 변위가 어느 수준 이상이 되면 최종상태라고 가정하는 정의를 활용하였다. 여기에서의 최적 설계는 러그 본체의 두께를 결정하는 것으로서, 비선형 해석 결과를 최적 구조설계에 사용하기 위해 러그 용량 별러그 본체의 두께를 변화시킨 여러 경우에 대한 비선형 해석결과로부터 3.4절에서 기술한 정의에 따라 최종강도를 구하였고, 이를 최적화 과정에 활용하였다. 전술한 바와 같이 최적 설계는 러그 본체의 두께를 결정하는 것으로써 ASME BTH-1 (ASME, 2008)에 제시된 설계기준의 안전계수 3.0을 최종강도가 만족하도록 T형 러그 본체의 최적 두께를 결정하였다. 본 연구의 결과에 의하면, 최종강도를 기준으로 한 최적 설계 결과가 설계 지침에 명시된 구조적 안전성의 수준 이상을 만족하면서 상당한 중량 감소를 얻을 수 있었다. 한편, 중량 감소의 양에 용량별 어떤 일관성이 있지 않는 것으로 보아 기존의 러그 설계 과정에 대한 검토가 필요할 것으로 생각된다.
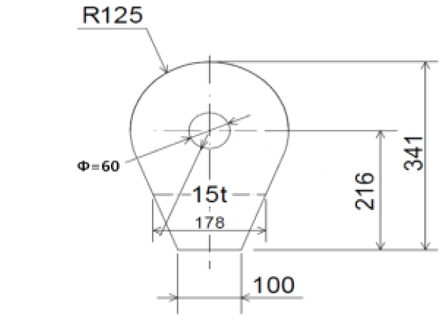
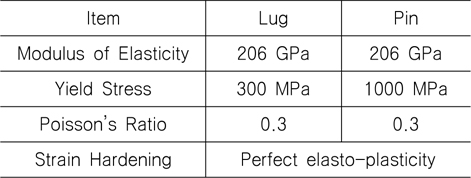
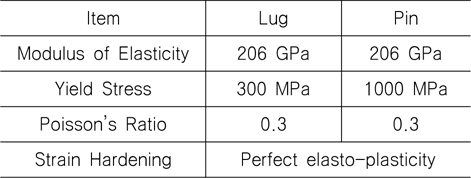
본 절에서는 본 연구에서 적용한 해석과정과 방법의 타당성을 검증하기 위하여 실험결과와 비교 및 검토하였다. 이를 위해 최근 Lee, et al. (2012)은 Fig. 1에 보인 러그 모델을 제작하여 Fig. 2에 보인 UTM(universal testing machine)을 이용하여 러그 모델에 대해 수행한 구조실험 결과를 본 연구의 해석결과와 비교해 보았다. 이 등의 시험용 러그 모델의 치수는 Fig. 3과 같고, 러그와 셔클 핀(shakle pin)의 재료적 특성치는 Table 1에 열거 하였다. 실험은 Fig. 3에 보인 바와 같이 UTM에서 러그 시편의 하단을 고정하고 러그 홀에 삽입한 셔클 핀(shakle pin)에 인장하중을 작용하여 실험을 수행하였다.
[Table 1] Properties of materials
Properties of materials
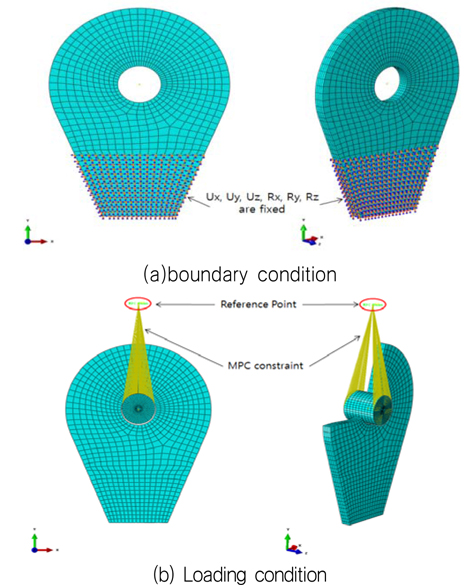
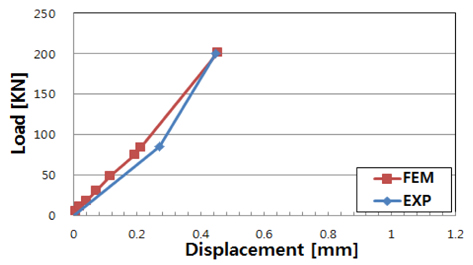
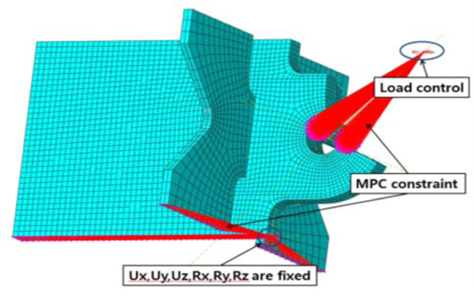
본 연구의 구조해석에서는 러그를 8 node solid element로 모델링하였고, 실험의 경우와 마찬가지로 Fig. 4(a)에 보인 바와 같이 러그의 하단 부분에 고정경계조건을 부여하였으며, 하중을 조정하기 위해 Fig. 4(b)와 같이 Reference point(RP)와 셔클 핀의 양단을 MPC Beam 요소로 연결하여 Reference point에 하중을 작용시킬 수 있도록 하였다. 구조해석은 비선형 해석을 수행하였으며 이때 재료적 비선형성은 Table 1에 보인 바와 같이 변형률 경화가 없는 완전 탄소성으로 가정하였다. 하중이 점차 증가할때 셔클 핀과 러그의 홀은 접촉된 상태가 유지되도록 하였다. 하중은 실험의 과정을 그대로 반영하였는데, 핀의 위쪽(y축) 방향으로 RP에 초기에는 84.4 KN을 작용 시킨 후 이어서 연속적으로 209 KN의 하중을 작용시켰다. 본 연구의 해석 결과와 실험결과의 비교로서 Fig. 5에 보인 바와 같이 하중-변위 곡선을 비교해 보았다. 변위는 하중 방향으로의 변위로서 Fig. 4에 보인 참고점(reference point)의 하중 방향으로의 변위이다. Fig. 5에서 보는 바와 같이 실험과 해석결과의 비교범위가 소성이 충분히 진행된 범위를 포함하고 있지는 못하지만, 어느 정도 비선형성이 발생하는 범위까지의 실험결과와 비교한 것으로서 본 연구에서 사용한 해석방법이 타당하다고 판단된다.
본 연구에서의 해석모델은 현재 조선소의 건조공정에서 사용되는 러그 중에서 선박 및 해양구조물 블록의 인양 및 반전 작업등에 많이 사용되는 T형 러그를 선정하였다. T형 러그의 전형적인 형상은 Fig. 6와 같다 (Min & Eum, 2011). 러그를 사용함에 있어 리그 홀 주변의 강도를 보강하기 위해 이중판(double plate)을 부착하였으며, 면외하중(out of plane load)에 의한 전도 방지와 블록과의 접촉력 제고를 위하여 러그 본체 양측면에 브라켓이 부착되어 있다.
Fig. 6에서 보듯이 T형 러그는 본체, 브라켓 그리고 러그 홀 주위의 이중 판(double plate)로서 3개의 부재로 구성되어 있다. 러그의 형상이 주어져 있다면 결국 설계는 이들 3개 부재의 두께를 결정하는 것이 된다. 만일 러그 홀 주변을 보강할 목적인 이중 판과 전도 방지용인 브라켓의 기능을 감안하여 이들의 두께에변화를 주지 않는다면 결국은 러그 본체의 두께를 결정하는 문제로 귀착된다. 구조해석의 결과로서 선형해석의 결과를 이용한다면 이 문제는 간단히 해결되지만, 비선형 해석을 통한 최종강도 를 기준으로 하는 경우에는 여러 경우에 대한 해석이 필요하게 된다. 본 연구에서는 ASME BTH-1 (ASME, 2008)에서 제시한 안전계수 3.0을 러그의 최종강도에 적용하여 이를 만족하는 최적의 본체 두께를 결정하였다. 즉, 최종강도가 러그 용량의 3배에 상당할 때의 본체의 두께를 결정하는 문제로 귀착된다. 여기에서는 용량이 20, 30, 40 그리고 50 ton인 4개의 T형 러그를 선정하였다.
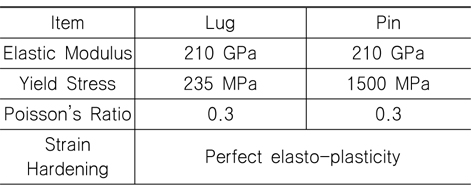
본 논문의 해석에 사용된 T형 러그의 재료는 연강(mild steel)으로 재료적 특성치는 Table 2에 열거하였다. 탄성계수는 210 GPa로 주었고, 항복응력은 연강의 공칭 항복응력인 235 MPa, Poisson 비는 0.3이다. 셔클 핀에 대해서는 항복응력은 연강인 러그 본체에 비해 높은 1500 MPa를 부여하였고, 탄성계수와 Poisson 비는 연강과 동일하게 210 GPa과 0.3으로 부여하였다. 탄소성 해석에 필요한 변형률 경화 계수(strain hardening coefficient)는 0으로서 응력-변형률의 관계는 완전 탄소성 거동(perfect elasto-plastic behavior)으로 가정하였다.
[Table 2] Material properties of T type lug
Material properties of T type lug
T형 러그에 적용된 경계조건과 하중조건은 전절에서 실험 모델과 비교를 위해 적용한 조건과 동일하다. 먼저 경계조건은 Fig. 7에 나타난 것과 같이 T형 러그의 본체와 브라켓이 블록에 부착되는 면에 있는 모든 절점에서의 모든 변위를 고정시키는 완전 고정 경계조건 (
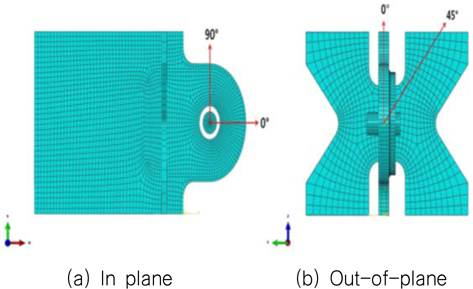
해석 시 T형 러그 각각에 적용된 하중의 방향은 아래의 Fig. 8에 나타나있는 것과 같이 면내하중(inplane load) 방향과 면외하중(out-of- plane load) 방향으로 정의된다. 러그의 최종강도는 면내 및 면외 하중의 방향에 따라 달라지는데, 현장에서는 면외 하중 방향이 15° 이내인 경우로 제한하고 있다. 본 연구는 면내 및 면외 하중 방향을 모두 고려하는 최적설계를 꾀하는 것이 아니라 러그의 강도측면에서 가장 불리한 하중 조건에서의 최적 설계를 다루는 것이므로 이 조건을 정의해야 한다. 면내 및 면외 하중 방향의 변화에 따른 강도 특성에 대해서는 Heo and Lee (2014)가 면내하중 방향은 0, 30, 45, 60, 90°와 면외하중 방향은 0, 15, 35, 45°에 대한 Parametric study를 수행한 바 있다. 그 결과에 따르면 면내 0°와 면외 45°가 가장 불리한 하중조건이었다. 물론 전술한 바와 같이 Fig. 8에서 면외 하중 방향이 45°인 경우는 실제 현장에서 사용하지 않지만 구조물 강도 측면에서 보수적인 결과를 도출하기 위해 여기에서는 면내와 면외 하중 방향이 각각 0°와 45°인 경우로 부여하였다.
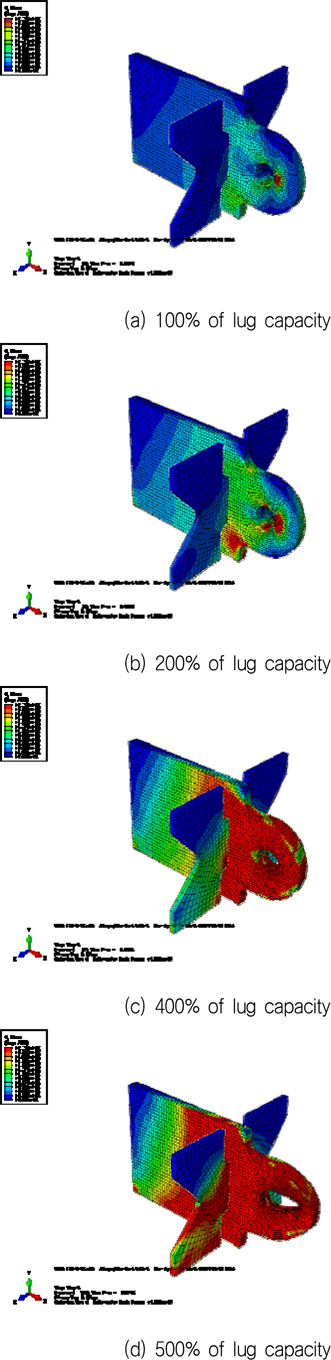
러그 본체의 두께 감소에 대한 최종 상태의 변화를 파악하기 위해, 전술한 바와 같이 하중 방향은 면내 0°와 면외 45°로 고정시킨 상태에서 러그 본체의 두께를 변화시켜가면서 비선형 해석을 수행하였다. 해석 결과의 예로서 Fig. 9는 용량이 20 ton인 T형 러그에 작용하는 하중이 각각 용량의 100, 200, 300, 400 그리고 500%인 경우 응력 분포와 변형 형상을 나타낸 것이다. Fig. 9에서 보듯이 하중의 크기가 점점 증가함에 따라 핀과 접촉되는 러그 홀 및 이중판 부분에 항복응력 수준의 응력이 발생되는 영역이 점차 넓어지고 러그 홀 주변에서의 변형이 심해지는 것을 알 수 있다.
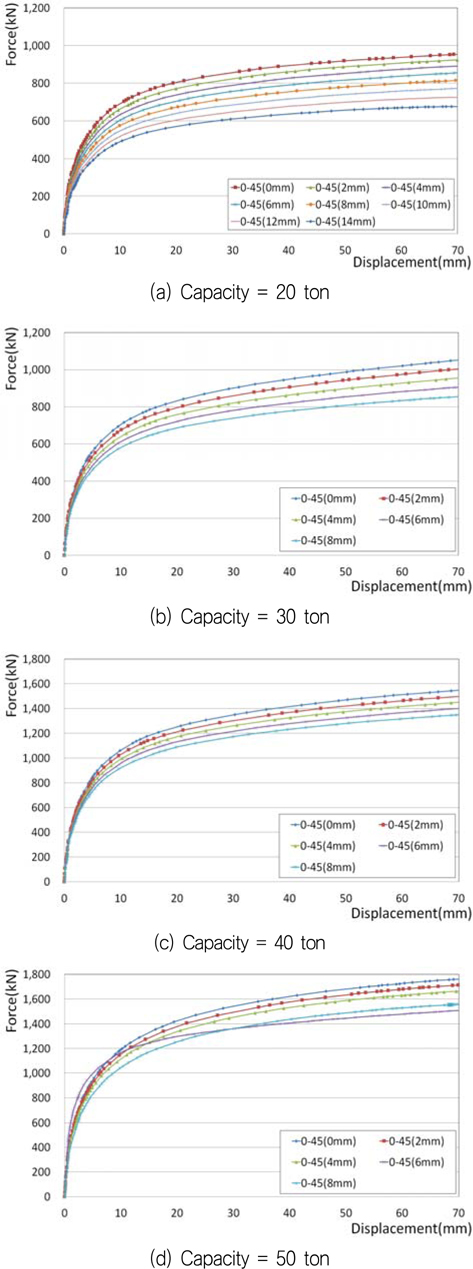
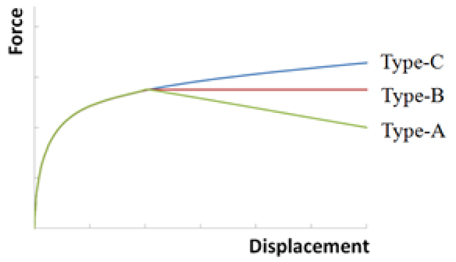
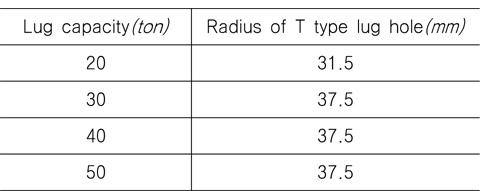
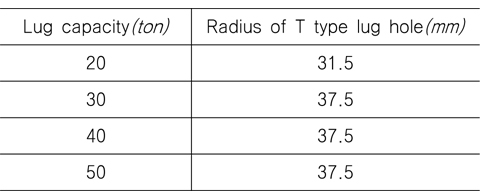
러그 용량별 본체의 두께 감소에 따른 하중-변위 곡선이 Fig. 10과 같다. Fig. 10에서 ‘0-45’는 하중 방향이 면내 0°와 면외 45°임을 의미하며 괄호 안의 숫자는 러그 본체의 두께의 감소량을 나타낸다. Fig. 10에서 보듯이 하중 증가에 따라 소성이 진행되기 때문에 어느 정도 이상의 하중을 초과하면 하중-변위 곡선의 기울기 즉, 접선탄성계수가 감소하지만 영(zero) 또는 음이 되지는 않고 변위의 증가에 따라 완만하긴 하지만 하중도 증가하여 최종 상태 (ultimate state)를 정의하는 것이 용이하지 않다. Fig. 11에 전형적인 하중-변위 곡선의 형상 3가지를 도시하였는데, Type A나 B의 경우에는 최종 상태를 정의하는 것이 용이하나 Type C의 경우에는 이를 정의하는 것이 용이하지 않다. 본 연구에서는 구조물이 상당한 수준의 변위를 경험하면 최종상태에 근접하는 것으로 간주하여, 하중 방향으로의 변위가 러그 홀 반지름의 50%정도로 큰 변위가 발생한 때를 최종 상태로 정의하였다(Lee, et al., 2014). 물론 이러한 최종 상태의 정의에는 논의의 여지가 있으나 본 정의를 일관성 있게 적용하는 데에 의미를 둘수 있고 또한 해석에 적용한 면내 0°와 면외 45°의 하중 방향이 실제의 경우 보다는 구조 강도 측면에서 보수적이라는 점에서 이러한 최종 상태의 정의를 이용한 설계 결과는 ASME에서 정한 안전계수 3,0 이상을 충분히 만족하므로 구조적 안전성은 보장된다고 볼 수 있다. 여기에서의 대상 러그 모델들의 러그 홀 반지름은 Table 3과 같다.
[Table 3] Radius of T type lug hole
Radius of T type lug hole
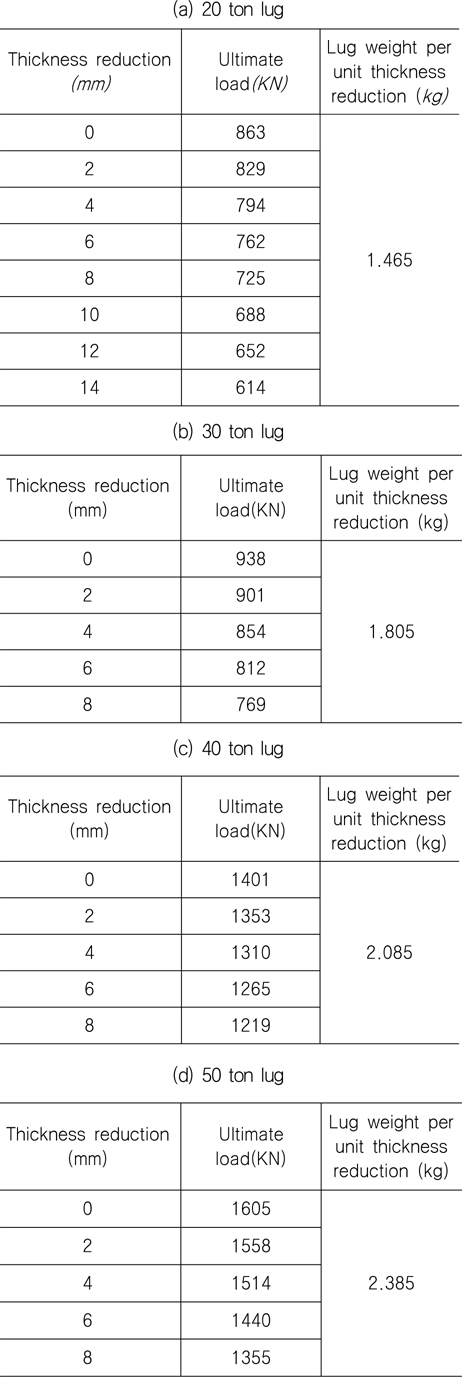
이러한 본 연구의 최종 상태 정의에 따라 Fig. 10의 결과로부터 구한 용량 20, 30, 40과 50 ton 러그의 본체 두께 감소량에 따른 최종 하중(ultimate load)을 Table 4에 정리하였다. Table 4에서 세 번째 열은 각 본체 감소량에 대응되는 러그 전체의 무게이다. 전술한 바와 같이 본 연구의 최적화 문제는 결국 최종 하중을 기준으로 안전계수를 만족하는 러그 본체의 두께 감소량을 구하는 문제로 귀착된다. 즉,
[Table 4] Ultimate load to thickness reduction
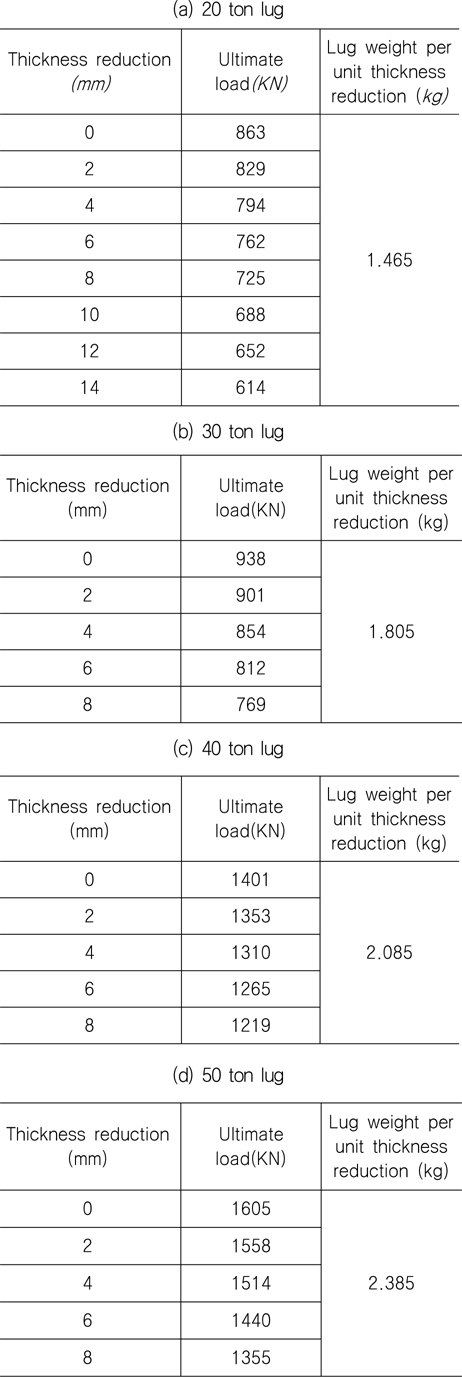
Ultimate load to thickness reduction
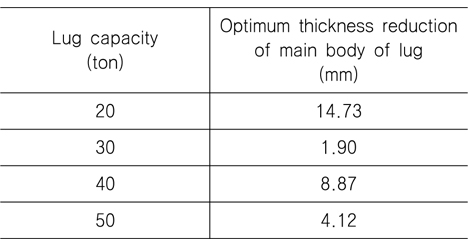
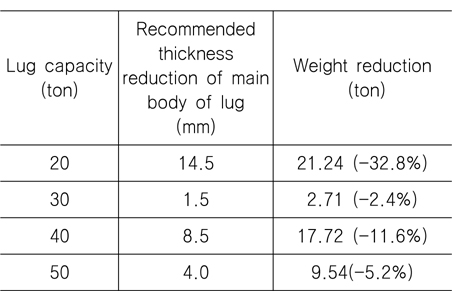
가 되는 러그 본체 두께의 감소량을 구하는 것이다. ASME 설계 기준 (ASME, 2008)에 따른 안전계수 3.0을 고려한 식(1)의 좌변인 각 용량별 러그의 최종강도는 각각 600, 900, 1200 그리고 1500 kN이다. Table 4에 열거한 각 용량별 러그 본체 두께 감소에 따른 최종강도에 관한 자료를 이용하고 식(1)을 만족하도록 최적화 과정을 거쳐서 구한 최적 설계의 결과로서 최적의 두께 감소량이 Table 5와 같다. 강판은 0.5 mm 단위로 생산되므로 Table 5에 보인 두께의 감소량은 이론적인 값이며, 실제로는 0.5 mm 단위로 감소시켜서 구조 안전성 제고를 위해 Table 5에 보인 두께 감소량 보다 작은 0.5 mm 간격의 값을 택해야 한다. 예를 들어서 20 ton 러그의 경우, 최적설계과정에 의하면 두께 감소량은 14.73 mm이나 이러한 두께 감소는 실제로는 이룰 수 없으므로 0.5 mm 간격으로 작은 값인 14.5 mm로 결정해야 한다. 러그 본체의 최종적인 두께 감소량과 그에 따른 러그의 중량의 감소량이 Table 6과 같다. 중량 감소량 우측에 괄호 안의 숫자는 최적설계 전 러그 중량을 기준으로 한 중량의 감소율이다. Table 6에서 보는 바와 같이, 최종 강도를 기준으로 구한 최적 설계결과에 의하면, 최종강도를 기준으로 해도 충분한 구조적 안전성을 보장하면서 기존의 설계 보다 상당한 중량 감소를 꾀할 수 있다는 것을 알 수 있다. 또한 본 연구에서 선정한 러그 모델들에 대해 용량 20 ton의 경우에는 32,8%의 중량 감소를 이룰 수 있지만 30 ton과 50 ton 용량의 경우 5% 이하의 중량 감소를 이룰 수 있는 등 최적 설계에 해당되는 러그의 중량 감소의 정도에 일관성이 없다. 이는 기존의 러그 설계의 기준에 대한 검토가 필요하다는 점을 의미하는데, 이 점에 대해서는 좀 더 많은 경우에 대한 해석 결과를 토대로 검토되어야 할 것이다.
[Table 5] Optimum thickness reduction of the present lug models
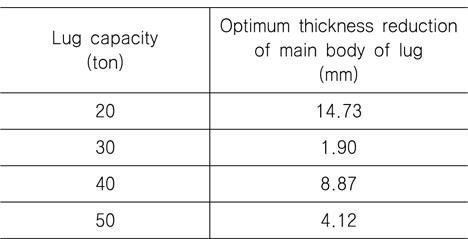
Optimum thickness reduction of the present lug models
[Table 6] Optimum thickness reduction and weight saving of the present T type lugs
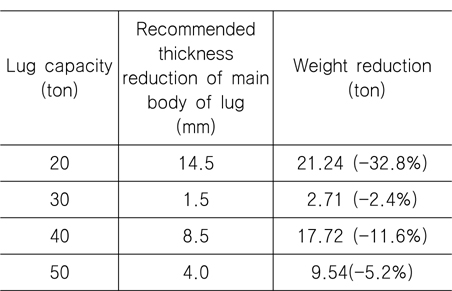
Optimum thickness reduction and weight saving of the present T type lugs
이상의 결과로부터 러그 구조 측면에서는 매우 불리한 하중조건을 기준으로 수행한 본 연구의 최적화 과정에 의하면 충분한 구조적 안전성을 가지면서 보다 경량의 러그 설계 결과를 구할수 있고, 이러한 과정을 적용하면 러그의 설계 및 제작에 효율성을 제고할 수 있을 것이다.
본 연구에서는 선박이나 해양구조물의 건조과정에서 블록의 인양과 반전과정에서 널리 사용하는 T형 러그의 최종강도를 기준으로 한 최적설계를 다루었다. 러그의 형상이 주어져 있다면, 러그의 설계는 본체, 브라켓 및 이중판의 두께를 결정하는 것이 되는데, 여기에서는 브라켓과 이중판의 두께에는 변함이 없다고 가정하였으므로 결국은 본체의 두께를 결정하는 문제로 귀착된다. 최종 강도를 기준으로 한 최적설계 결과를 도출하기 위해 본 연구에서는 우선 러그의 비선형 해석 결과로부터 최종상태를 정의하는 부분을 언급하였고 그 결과를 이용하여 주어진 안전계수를 만족하는 최적 설계 결과로서 러그 본체의 두께를 결정하였고 그에 따른 러그 중량의 감소량을 산출하였다. 본 연구 결과에 따르면 대상으로 선정한 러그 모델에 대해 최종 상태를 기준으로 한 설계결과가 상당한 중랭 감소를 꾀할 수 있음을 알 수 있었다. 또한 중량 감소량에 일관성이 부족한 점으로 보아 기존 설계에 대한 검토가 필요할 것으로 사료된다. 본 연구의 최적설계 과정은 이중판 및 브라켓의 두께도 설계 인자로 선정한 최적 설계에 적용할 수 있을 것이다.