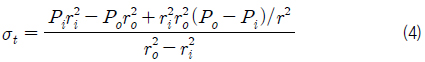최근 해양플랜트산업의 활성화 필요성이 인지되고 있으나 산업의 구성품인 기기의 국산화는 쉽지 않은 현실이다. 산업 특성상 고가, 소량, 기술집약적인 제품이 많고 대부분 석유가스 산업이 발달한 지역을 기반으로 하기에 국산화가 어렵다. 해양플랜트에서 바다 속에서 사용되는 제품군은 내압에 관한 설계나 제작이 필연적인데 국산 제품이 적다 보니 내압설계에 관한 기본적인 연구내용과 체계가 없는 것 또한 현실이다. 각종 센서로 부터 Sub-sea, Pipe 까지 설계에 관한 국외의 규정들이 (예 ASME, API) 정립되어 있고 또한 각 선급 (ABS 등)에서도 자체 규정들을 제시하고 있으나, 국내에서는 구체적인 내압용기에 관한 연구 사례가 적다. 특히, 조선해양분야의 내압용기에 관한 연구 발표는 매우 적은 편이다. 1991년 국내에서 심해용 압력용기 붕괴해석이 발표되었다 (Shin & Yoo, 1999). 당시 대우조선에서 소형 잠수정 (옥포 6000)을 개발하기 위한 연구였다. (Jeong, et al. 2004)에 의해 6000
본 연구에서는 ASME 내압용기 첫째 기준에 해당하는 심해 2000
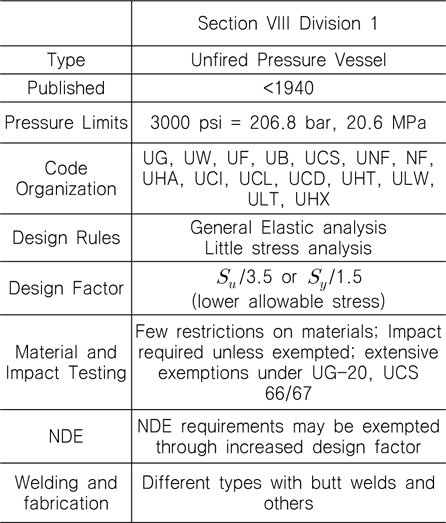
내압용기 설계는 외압과 내압의 경우에 큰 차이가 있는데, 외압의 경우 좌굴에 대한 고려를 해야만 한다. ASME BPVC (Boiler and Pressure Vessel Code) VIII에는 3개의 Division이 있고 Table 1에 Division 1에 대한 주요한 요소들이 있다.
[Table 1] ASME Section VIII for pressure vessel
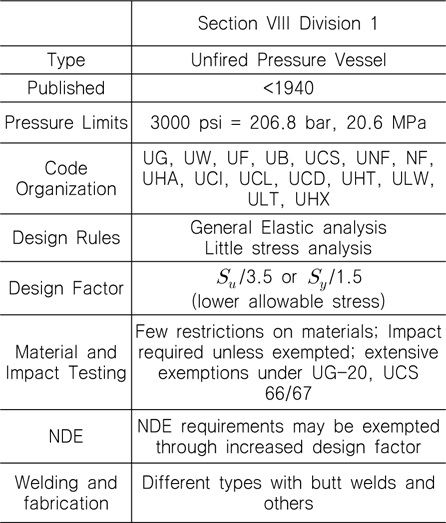
ASME Section VIII for pressure vessel
Division 1; Rules for Construction of Pressure Vessels
Division 2; Alternative Rules
Division 3; Alternative Rules for Construction of High Pressure Vessels
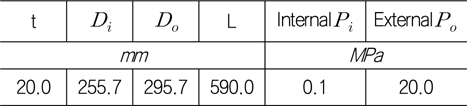
본 연구에서 내압용기는 총길이 650
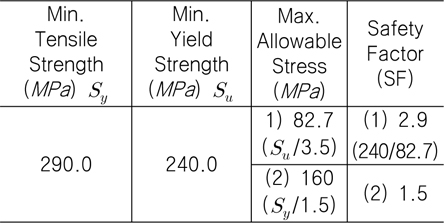
[Table 2] AA 6060-T6 Material properties

AA 6060-T6 Material properties
ASME 규정에 의한 설계 과정은 아래와 같다.
P1. 본 내압용기의 경우 길이와 외경 값은
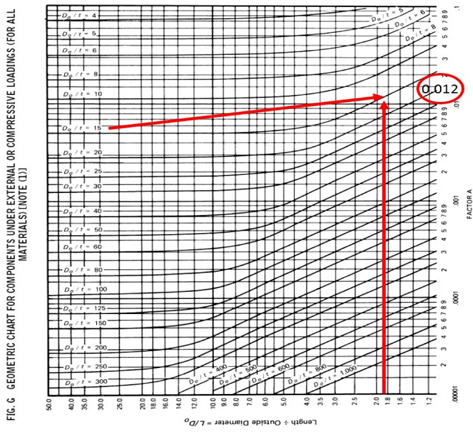
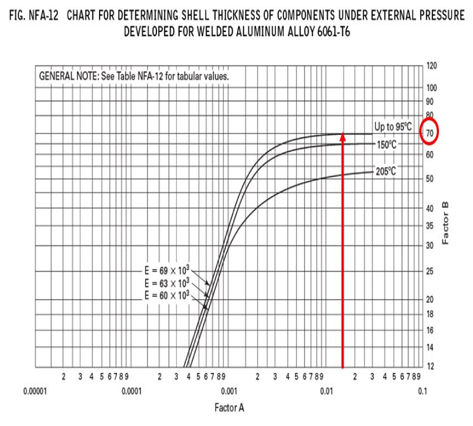
P2. Fig. 1의 ASME Section II Part D 의 SUBPART 3, FIG.G 에서 FACTOR A를 정한다. 이 때,
P3. ASME 규정의 Eq. (1)에 의해 허용하중(압력)
여기서,
본 내압용기의 경우
[Table 3] Dimension of cylinder
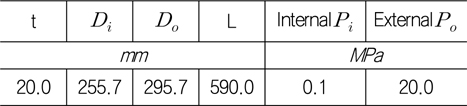
Dimension of cylinder
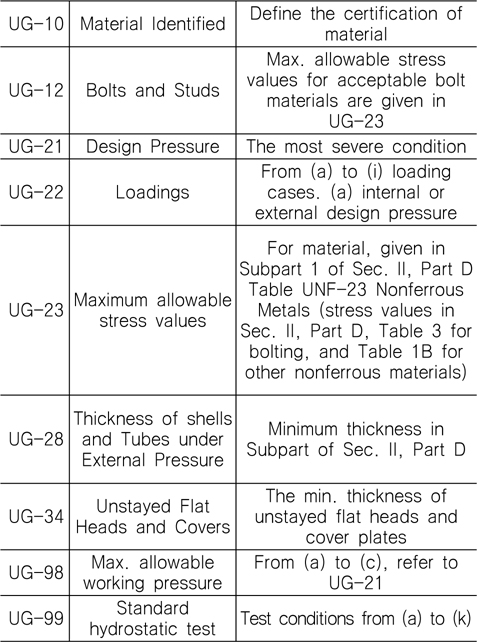
Division 1 에 의거하여 설계의 기본이 되는 코드 Part UG; General Requirements for all Methods of Construction and All Materials에서 제품과 관련된 부분을 다음과 같이 Table 4에 정리하였다. Fig. 3의 내압용기는 연구용 시료이기 때문에 용기가 사용되는 환경(온도), 제품의 용접, 제작과정, 마킹, 검사 등의 내용은 생략되었다. Table 4에 의한 내압용기 설계과정은 다음과 같다.
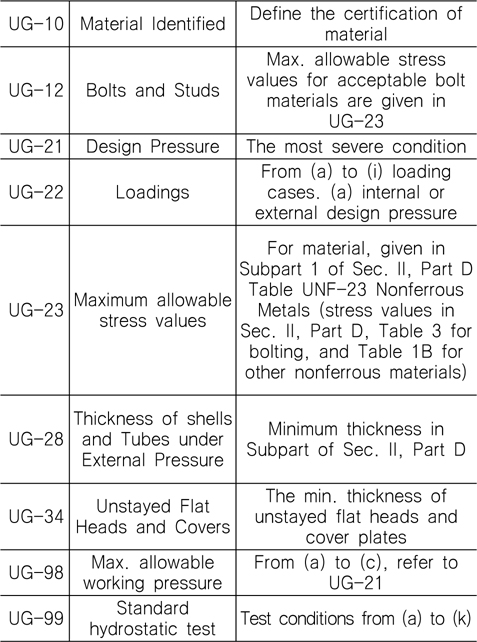
ASME UG procedure
(1) UG-10; 해양용으로 사용되는 알루미늄 AA 6061-T6 bar를 가공하여 제작하였다.
(2) UG-12; 덮개용 볼트는 8개이고 M6를 사용한다.
(3) UG-21; 설계하중은 수압 200 bar 이다.
(4) UG-22; 현재는 압력용기 내압 (1
(5) UG-23; ASME 규정에 의한 알루미늄 6061-T6 허용응력인 82.7
(6) UG-28; Lame 식에 의한 두꺼운 압력 실린더 식에 의하여 두께가 계산되었고 ASME 허용하중을 만족한다.
(7) Ug-34; 평평한 덮개가 적용되었다. ASME에서 추천하는 덮개 양식에는 해당되지 않는다.
(8) UG-98; 제품이 작용중인 허용 압력은 수압 200
(9) UG-99; 이 시험은 내부에 압력이 있는 용기에 대한 것이고 본 시험에는 미 국방성 시험표준 (MIL-STD-810G)이 수행되었다.
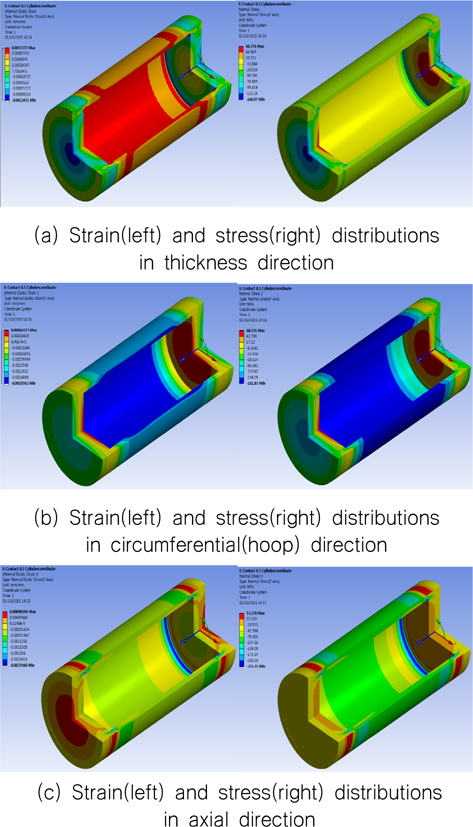
현재의 ASME 규격에 의한 알루미늄 재질과 설계 치수의 압력 실린더에서 항복응력 240
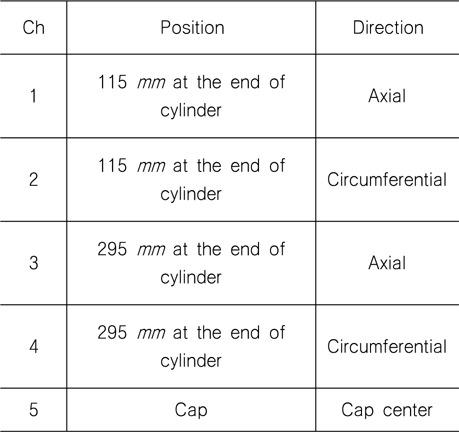
ANSYS Solid 요소 3040개를 사용하였고 덮개와 실린더가 만나는 부분의 접속조건은 Bonded가 사용되었다. 해석 시 산출 된 스트레인(변형률) 값이 큰 3점(Location A, B, C)의 위치에 스트레인 게이지를 부착하여 내압실험을 진행하였다. Location A, B, C 는 내압용기 끝단에서 115
[Table 5] Location of five strain gauges
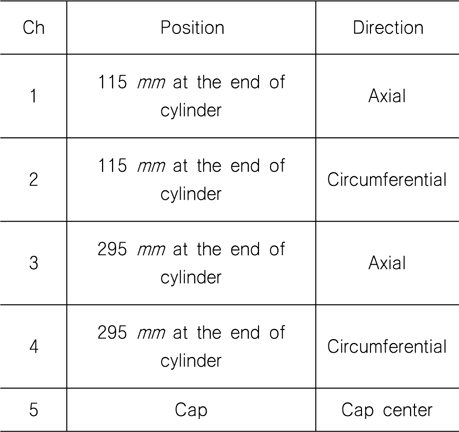
Location of five strain gauges
사용압력인 200
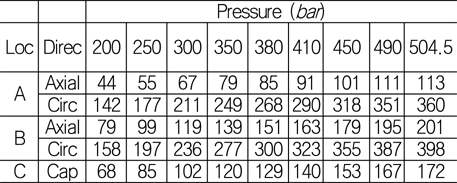
[Table 6] Stress values (MPa) for applied pressure at cylindrical external surface
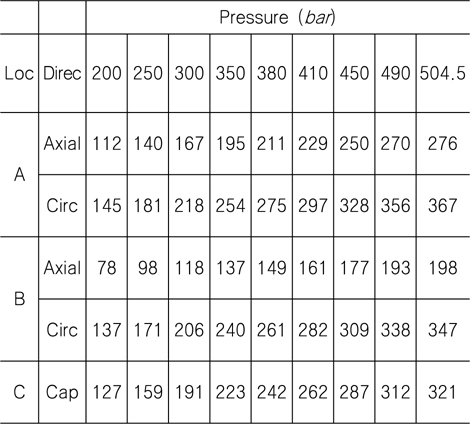
Stress values (MPa) for applied pressure at cylindrical external surface
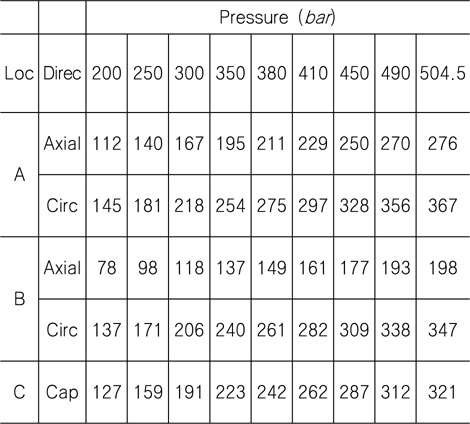
[Table 7] Stress values (MPa) for applied pressure at cylindrical internal surface
Stress values (MPa) for applied pressure at cylindrical internal surface
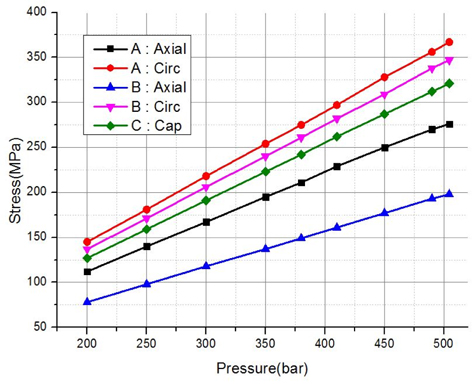
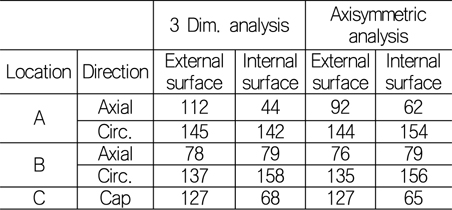
Fig. 5는 해석 된 응력 값의 그래프인데 선형해석이므로 해수압이 증가함에 따라 응력도 선형적으로 증가함을 볼 수 있다. Two dimensional 해석인 Axisymmetric 응력 해석의 경우, 수압 200
[Table 8] Comparison of Stresses(MPa) between 3D & axisymmetric analysis for 200 bar
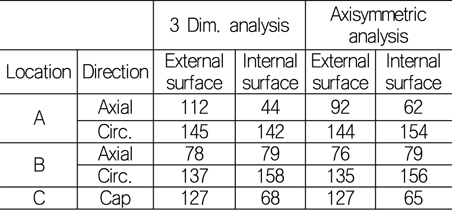
Comparison of Stresses(MPa) between 3D & axisymmetric analysis for 200 bar
치수 설계 후, 내압용기 시료 제작에 앞서 AA 6061-T6에 대하여 공인 시험기관에서, 금속재료의 인장시험법인 KS B 0802 규격에 따라, 항복강도와 인장강도 및 연신율을 구하였다. 총 5개의 시료 (Fig. 6) 시험 결과 인장강도는 평균 385.4
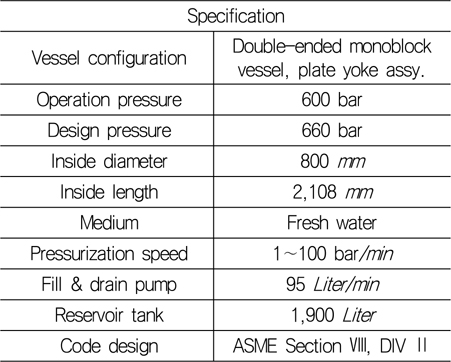
제작된 내압용기로 선박해양플랜트연구소에 설치된 고압챔버를 이용하여 내압시험을 수행하였다. 시험에 이용된 고압챔버의 형상과 주요사양은 Fig. 7, Table 9와 같다.
[Table 9] Specifications of KRISO’s hyperbaric chamber
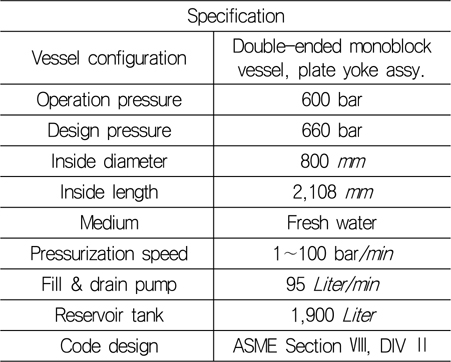
Specifications of KRISO’s hyperbaric chamber
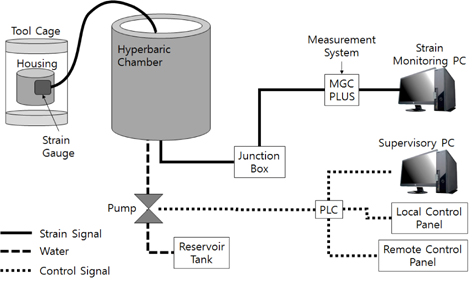
내압시험을 위해 Fig. 3과 같이, 스트레인 게이지의 부착 위치는 유한요소 해석 결과를 바탕으로, A 점, B 점과 C 점으로 선정하였다. 해석결과, A와 B 점에서는 축 방향과 원주방향 스트레인 측정을 위해 90° T Rosette 방식으로 부착하였고, 덮개 중심은 모든 방향이 동일하므로 1개의 게이지를 부착하여 총 5개의 스트레인 게이지를 부착하였다. 시험에 사용된 게이지 및 부속재료는 독일 HBM社 제품(K-LY-43-6/350)을 사용하였고, 게이지의 표면 방수를 위해 Putty 재질의 표면 보호제를 사용하였다. 시험 설비 및 스트레인 계측 시스템의 구성은 Fig. 8과 같다. 게이지와 연결된 신호선은 고압챔버 바닥의 관통구에 설치되어 있는 커넥터를 통해 외부 계측기에 연결하여 스트레인을 측정할 수 있도록 시스템을 구축하였다. 모든 연결을 완료한 후 내압용기를 보조용 치구에 고정한 후 고압챔버 내부에 배치하여 시험을 진행하였다. 시험은 고압챔버의 상단 덮개를 닫은 후에 고압챔버 내부에 시험용수(청수)를 채워 정해진 시험 조건에 따라 가압 및 유지하는 형식으로 진행하였다. 전체적인 시험 과정은 Fig. 9와 같다.
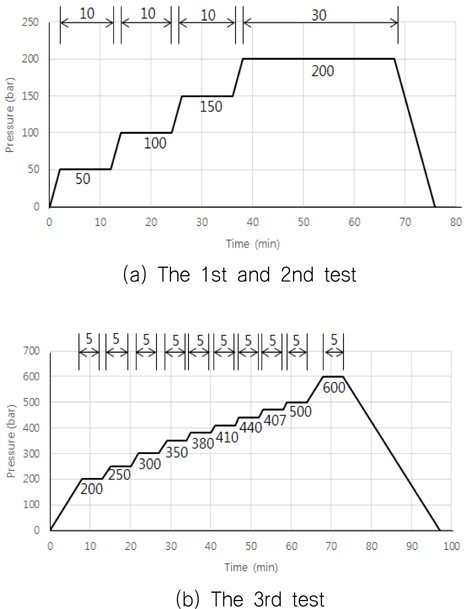
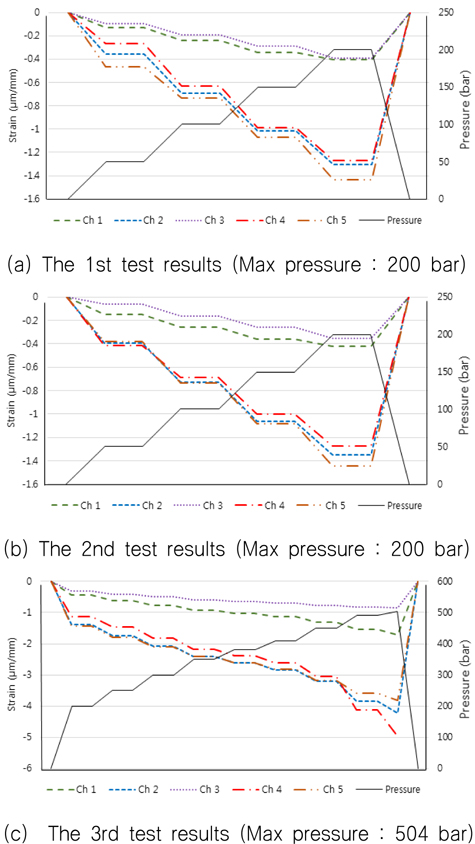
1차와 2차 내압시험은 미 국방성 시험표준(MIL-STD-810G)을 적용하여 운용압력 200
1차와 2차의 각 시험 결과는 거의 유사하여 Fig. 11 (a)와 (b)에 있다. 압력별 스트레인 결과는 Table 10에 있는데 축 방향 게이지인 위치 A의 채널 1과 위치 B의 채널 3의 최대압력 200
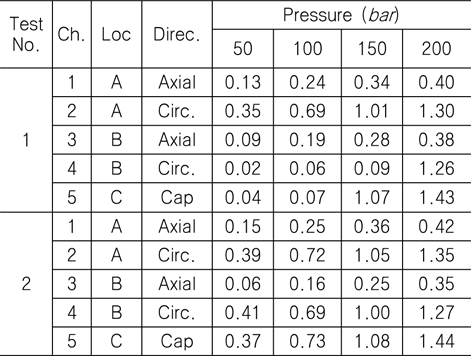
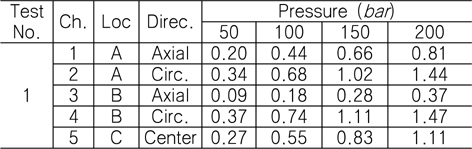
[Table 10] Strain result for 1st and 2nd chamber test: 50 ~ 200 bar (unit: ㎛/mm)
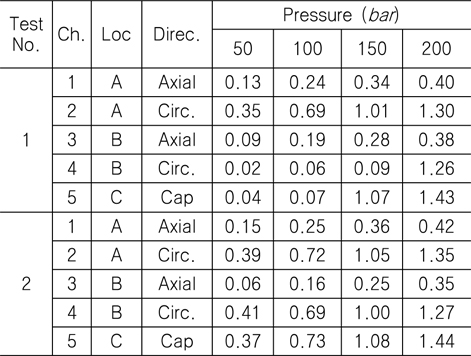
Strain result for 1st and 2nd chamber test: 50 ~ 200 bar (unit: ㎛/mm)
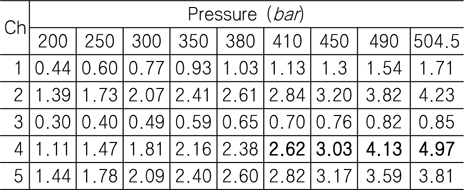
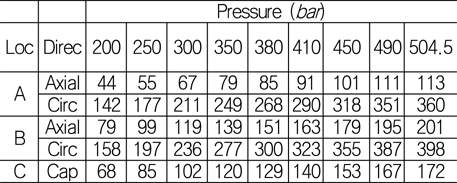
3차 시험의 결과는 Fig. 12 (c)와 같고, 압력별 스트레인 결과는 Table 11에 있다. 200
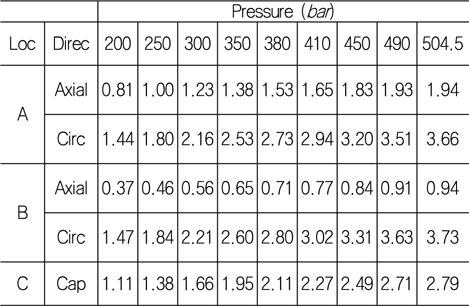
[Table 11] Strain result for 3rd test chamber test: 200 ~ 504.5 bar (unit: ㎛/mm)
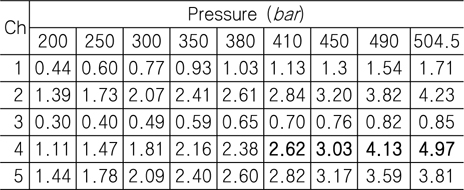
Strain result for 3rd test chamber test: 200 ~ 504.5 bar (unit: ㎛/mm)
Table 10 에서 중앙부위 B에서, Circ. (hoop) 방향 스트레인 값들이 Axial 방향에 비해 4배 이상 큰 것을 알 수 있다.
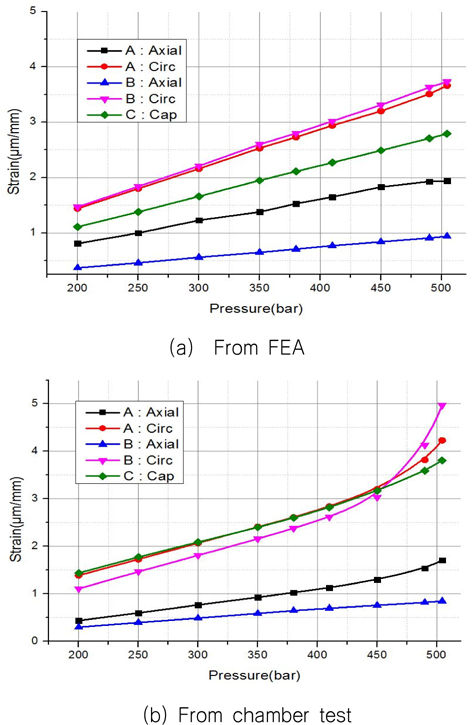
구조해석에서 산출된 스트레인이 Table 12와 Table 13에, 시험에서 구한 값이 Table 10과 Table 11에 있다. 이중 수압이 200
[Table 12] Strain result for FEA : 50 ~ 200 bar (unit: ㎛/mm)
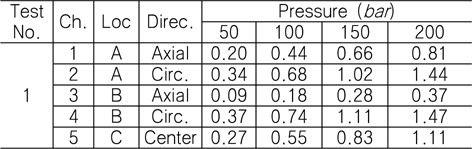
Strain result for FEA : 50 ~ 200 bar (unit: ㎛/mm)
[Table 13] Strain results for FEA : 200 ~ 504.5 bar (unit: ㎛/mm)
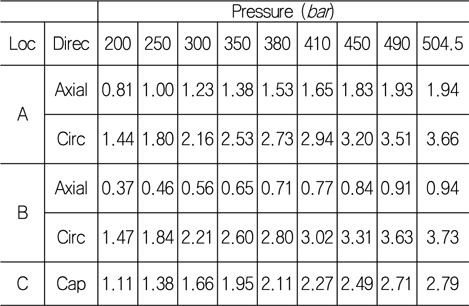
Strain results for FEA : 200 ~ 504.5 bar (unit: ㎛/mm)
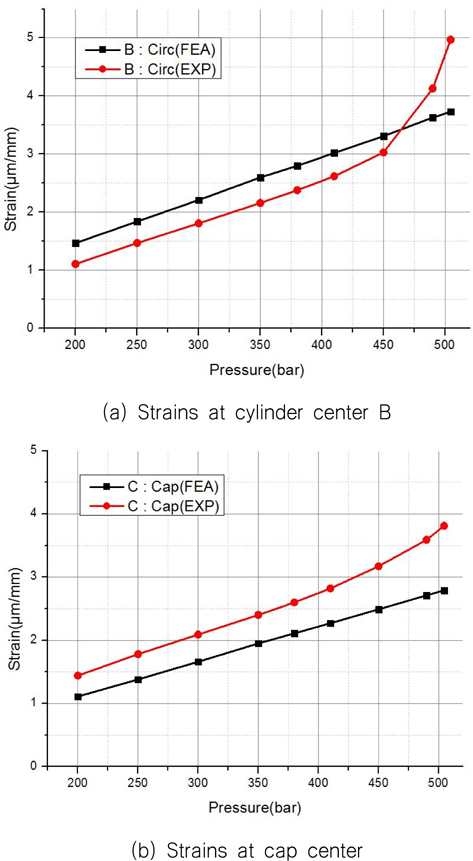
내압시험의 스트레인 값이 정확하다는 가정아래, Table 10 과 Table 11을 분석하면 덮개와 가까운 A점에서의 Circ. 방향은 해석과 시험 값이 비슷하다. 항복에 가까우면 시험 값이 더 커진다. 항복이 먼저 발생하는 중앙점 (B)의 Circ. 방향에서 해석 값이 대체로 약 20% 정도 크지만, 410
해석에서는 덮개 전체가 실린더와 접속되어 있어 실린더의 경계부분이 견고하므로 중앙부의 스트레인이 적게 산출된 것으로 보인다. 시험의 경우 볼트 8개가 원주 방향을 모두 고정할 수 없어 (단순지지의 경우처럼) 중앙부의 스트레인이 작은 것으로 보인다.
1. 국제규격인 ASME 규정에 의하여 설계를 진행하였으나, 규정에 적용된 알루미늄 재질의 강성이 실제 실험 시 적용된 시료의 재질보다 약하여 시험이 어려울 수 있었으나, 본 연구에서는 안전계수를 낮추어 설계를 한 후 압력챔버 시험을 수행하였다. 설계 전에 사용 될 알루미늄의 재질에 대한 문헌이나 규정의 자료보다는 실제 재질에 대해 정확하게 파악하는 것이 무엇보다 중요하였다.
2. 유한요소 해석의 응력값 분석을 통해 챔버시험시의 스트레인 게이지 부착위치와 방향을 결정하였다. 해석과 시험의 스트레인 값의 경향은 대체로 일치하였고 일부 구간에서 최대 20여 퍼센트의 차이를 보였다. 이론에서 제시된 바와 같이 Hoop 방향 응력이 축방향 응력 보다 크게 나오며 두께 방향 응력은 수압 값과 같게 나왔다. 위치 A 점 (115
3. 챔버시험 시, 사용된 알루미늄의 인장시험에서 도출된 항복응력 값에서 항복이 발생함을 알 수 있었다. 이는 내압용기 중앙 위치에서 스트레인 값이 410
4. 본 연구에서는 심해저용 압력챔버로 시험할 수가 있어 기존에 발표된 연구보다 좀 더 진일보된 구체적인 결과가 도출되었다. 향후, 재료의 특성이 설계 규정과 다른 현실적인 문제를 해결해야 하는 점과 강철이나 티타늄 등의 재질로 2000
5. 이번 시험을 통하여 덮개 부분이 다소 취약한 점이 인지되었다. 향후, ASME 규정에 의한 덮개 설계로 시편을 만들 필요가 있고, 유한요소 해석에서도 덮개와 실린더의 접속 조건과 볼트를 고려한 모델을 통하여 시험결과와 비교하여 시험과 해석의 관계를 더 면밀히 분석하여 규정에 기반한 설계에 참조할 필요가 있다.