LNG(Liquefied natural gas) 선박은 −163℃의 극저온 상태를 유지하며 액체상태로 안전하게 운송해야 하기 때문에 LNG 탱크내에 화물창을 설치하여 화물을 보관한다. LNG 화물창은 IMO에서 제시된 규정에 따라 선박의 선체에서 독립적으로 구성된 독립형 탱크와 선체에 부착된 일체형 형태인 멤브레인 탱크로 구분된다. 최근 개발되는 독립형 탱크의 경우 Torgy LNG 사에서 제시한 Prismatic 형태의 IMO-A 타입 탱크가 개발되었으며, 일본의 MHI 사에서 개발하여 Sayaendo Series LNG 선에 적용된 B 타입 탱크가 있으며, 열손실을 최소화하기 위해 NLI Innovation AS 사에서 개발한 Prismatic 형태의 B 타입 탱크가 있다. 또한 C 타입 탱크의 경우 Aker Engineering에서 알루미늄 이중 방벽을 적용하여 제시된 바 있다. 멤브레인형 화물창의 경우 대표적인 제조사인 GTT 사와 대형 조선사에서는 화물창의 단열 및 구조성능을 개선시킨 다양한 형태의 멤브레인형 화물창을 제안하고 있다(Johan, 2015).
GTT 사의 경우 기존 NO96의 단열성능을 향상시키기 위해서 내부재를 기존 펄라이트에서 글래스울로 변경한 NO96 GW 모델과 방벽의 수를 증가시켜서 단열성능을 향상시킨 L03 모델을 제시한 바 있고, Mark III 화물창을 개선한 Mark III Flex와 Mark V모델을 소개하였다(GTT, 2014). 또한 국내 조선사인 HHI에서는 SUS와 Invar 멤브레인 재료를 적용하여 2차 방벽으로 구성된 HC-10 화물창을 소개하였고, 한국가스공사에서도 멤브레인형 화물창인 KC-1 모델을 개발하였다. 또한 SHI에서는 2차 방벽에 PU 접착법을 적용한 SCA-MCL 모델과 SCA-WS 모델을 소개하였다(Jin et al., 2013; Lee et al., 2103; Kim et al., 2009).
화물창의 설계단계에서는 −163℃의 극저온 유체화물을 안전하게 운송해야 하기 때문에 단열성능 및 구조안전성에 대해서 엄격하게 평가하고 있다. 화물창의 단열성능 평가하는 지표는 BOG(Boil off gas), BOR(Boil off rate)로서 선급 및 선주가 제시한 단열성능의 요구사항을 만족하기 위해서 화물창의 구조는 R-PUF(Reinforced polyurethane form) 및 펄라이트 등의 다양한 단열재를 이용하여 다층의 방벽으로 구성되어 있다. 구조안전성을 만족하기 위해서 액체 화물 적재로 인한 정수압, 선체의 변형에 의해 발생하는 외력조건, 극저온 온도분포에 의한 열하중 및 유체화물이 적재된 선박의 운동에 의해 발생하는 슬로싱 하중 등에 대한 구조강도 평가가 선행되며, 선급에서 제시한 강도평가 기준을 만족하여야 한다. 일반적으로 화물창의 강도 평가 기준은 DNV 선급에서 제시된 GASA (General approval for ship application)의 승인을 받아야 하며, 평가항목은 크게 온도하중 및 정수압 등의 하중이 고려된 정적강도 평가 기준과 선체 운동 시 발생하는 슬로싱 하중에 대한 강도평가 과정으로 진행된다(Johan, 2015).
본 연구에서는 국내 조선사인 대우조선해양에서 현재 개발중인 새로운 형태의 멤브레인형 화물창을 개발하기 위하여, 선급에서 제시하는 평가기준을 만족하기 위한 정적 강도 평가 기법에 대해서 연구하였다. 제시된 멤브레인형 화물창은 2개의 단열 방벽으로 구성되어 있으며, 액체화물의 유출을 방지하기 위하여 SUS(Stainless steel)재질의 멤브레인을 적용하고 있고, 두 개의 방벽은 결속장치(Securing device)에 의해서 결속되어 있는 구조이다. 멤브레인 화물창의 정적 강도평가 모델은 화물창을 구성하는 주요 단열 부재들의 강도평가를 위한 전역(Global) 해석 모델과 방벽의 결속장치의 안전성을 판단하기 위한 국부(Local) 해석 모델로 구성되어 있으며, 강도평가 모델에 적용된 하중조건으로는 극저온 액체에 의한 온도하중, 액체 화물에 의한 정수압 조건이 변위로서 반영되어 있다. 제시된 강도평가 모델은 적용된 하중조건에 대해서 화물창의 강도를 평가하기 위해서 정적강도평가를 위한 하중 비선형해석이 수행되었으며, 정적강도 해석 후 결과를 통해 제시된 모델의 타당성에 대해서 검토하였다.
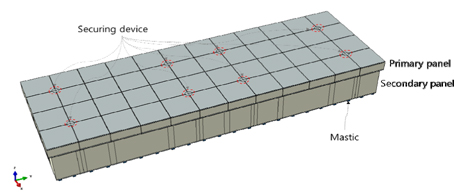
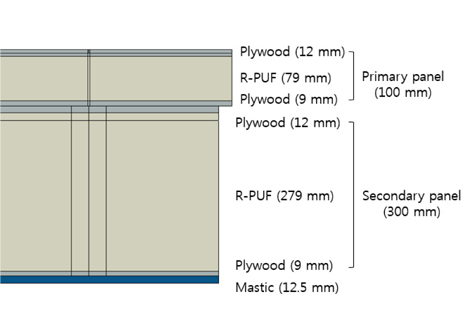
LNG 화물창의 구조는 LNG 액체 화물의 단열을 위한 1차 방벽(Primary panel)과 2차 방벽(Secondary panel)으로 구성되어 있으며, 두 개의 방벽은 결속장치에 의해 8개 지점에서 결속되어 있다. 따라서 액체화물에 의한 열하중 및 액체화물에 의한 정수압 및 슬로싱 하중에 의해 변형이 발생할 경우 두 개의 방벽은 서로 접촉이 발생하면서 수축과 팽창을 하는 구조로 구성되어 있다. Fig. 1은 멤브레인 LNG 화물창의 단위 단열창을 보여주고 있으며, 단위 단열창의 길이와 폭은 약 3x1m의 치수를 가지고 있다. 각 방벽은 Fig. 2에서와 같이 −163℃의 극저온 유체화물의 단열을 위한 Plywood와 R-PUP(Reinforced polyurethane form) 재료로 구성되어 있으며, 1차 방벽은 100mm의 높이를 가지도록 구성되어 있고, 2차 방벽은 300mm의 높이로 구성되어 있다. 또한 유체화물과 접하는 1차 방벽의 상부와 2차 방벽의 상부는 유체화물을 유출을 방지하기 위한 위한 SUS 재질의 멤브레인이 부착되어 있다.
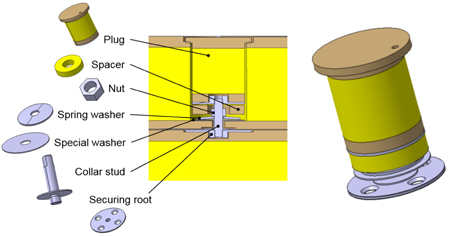
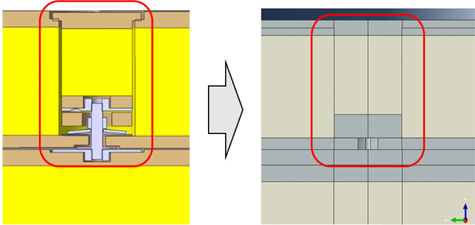
결속장치는 멤브레인 화물창의 8개의 지점에서 2차 방벽에 고정되어 1차 방벽을 결속시켜주는 장치로서, Fig. 3에서와 같이 구성되어 있다. 이 중 Securing root는 2차 방벽의 상부 Plywood에 볼트로 결속되어 고정되어 있고, 그 위에 Collar stud, Washer, Nut, Plug 의 부재가 조립되어 1차 방벽을 고정시키는 역할을 한다. 또한 결속장치와 1차 방벽의 변형을 허용하도록 측면으로 약 5mm의 공간을 가지도록 설계되어, 극저온 화물이 적재되었을 경우 1차 방벽의 수축과 팽창을 허용하도록 설계되어 있다.
멤브레인 화물창의 구조안전성 평가는 화물창에 작용하는 하중 조건에 대해서, 각 부재의 안전성을 평가하기 위한 전역(Global) 구조 강도 평가와 화물창의 상하부 방벽을 연결하는 결속장치를 평가하기 위한 국부(Local) 해석으로 나뉘어 평가하였다.
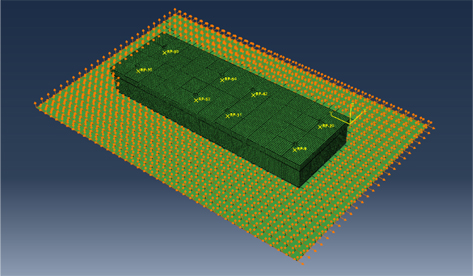
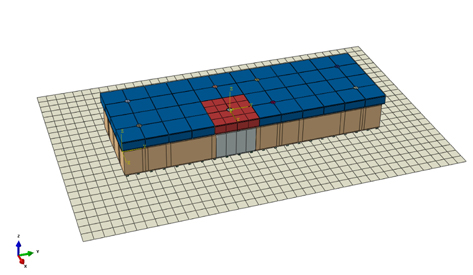
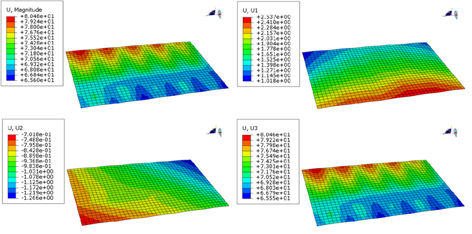
액체 화물이 적재된 LNG 탱크 내에서 발생하는 유체 화물의 하중 및 극저온 온도에 대한 화물창의 강도평가를 수행하기 위해서 Fig. 4에서와 같이, Mastic에 의해 LNG 선박의 내부 선체에 화물창이 부착된 형태로 구성하였다. 선체 구조는 Web. 및 Longi. 부재들이 생략된 평판 형태로 구성되어 있으며, LNG 선박에 작용하는 외력 및 발라스트에 의한 정수압 조건에 대한 선체의 국부 변형을 고려하기 위해서 Fig. 5에서와 같이 전선해석 결과 중 변위값이 내부 선체 구조의 초기조건으로 부여되었다. 또한 화물창의 연속성을 반영하기 위해서 측면인 4면에는 대칭조건을 부여하였다.
본 연구에서 검토하는 화물창의 구조는 2차 방벽이 선체와 접합되어 있고 1차 방벽은 결속장치에 의해 구속되어 있다. 따라서 변형 발생 시 1차 방벽은 2차 방벽의 수평방향으로는 변형이 발생하여 슬라이딩이 발생하는 형태이고 수직방향으로는 결속장치 에 의해 구속되어 있는 구조이다. 따라서 이러한 화물창의 구조적 특징을 반영하기 위해서 1차 방벽과 2차 방벽은 접촉조건을 부여하여, 1차 방벽에서 변형 발생 시 수평방향에 대해서는 슬라이딩이 발생 할 수 있도록 구성하였으며, 수직방향으로는 구속이 되도록 구성하였다. 또한 화물창과 선체의 결합된 상태에서 구조응답 계산 시 계산의 효율성을 위해서 모델의 세부형상을 단순화하여 모델을 작성하였다. 단순화가 적용된 구조는 Fig. 6에서와 같이 결속장치의 복잡한 형상을 삭제하고 단순화된 원기둥(Cylinder) 형상으로 대체하여 적용하였다. 이때 수직방향 변위 구속 및 Washer 등의 부재들의 효과를 구현하기 위해서 자유도 구속(Degree of freedom coupling)과 Collar stud 부재의 강성을 단순한 수직 스프링(Vertical Spring) 모델링 방법을 사용하여 적용하였다.
멤브레인 LNG 화물창의 유한요소해석모델에 사용된 요소는 Reduced 적분법을 사용하고 hourglass control이 적용된 8-node linear brick 요소를 사용하여 구성하였다. 분할된 요소의 사이즈는 10mm를 기준으로 하여 분할하였으며, 1차 방벽과 2차방벽의 상하부 Plywood는 두께방향으로 요소가 2개의 층을 가지도록 분할하고, Mastic의 경우도 두께 및 폭 방향으로 2개의 층을 가지도록 분할하였다. 선체모델의 경우 전선해석 모델에서 해석부위를 선정하여 사용하였기 때문에 4-node shell 요소로 구성되어 있다.
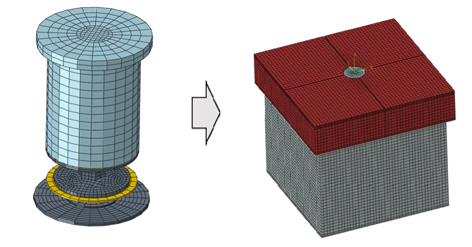
국부 해석 모델은 화물창의 구조에서 1차 방벽의 결속장치의 구조강도를 평가하기 위해서 수행되었다. 국부 해석 수행시 전역 해석 모델과 분할하여 해석을 수행하게 되면, 하중조건이 중복되어 반영될 수 있는 문제점을 방지하고, 화물창의 변형에 대한 거동을 보다 정확하게 반영하기 위하여 Fig. 7에서와 같이 결속장치를 상세하게 모델링하고, 평가하고자 하는 부위를 화물창에 결합하여 모델을 구성하였다. Fig. 8은 전역 해석 모델과 결합된 국부 해석 모델을 보여주고 있으며, 모델간의 경계면은 접착(Bonded) 조건을 적용하여 모델을 구성하였다. 국부 해석 유한요소 모델에 사용된 요소는 전역 해석 모델과 동일한 요소를 사용하였으며, 사이즈는 2mm를 기준으로 분할 하였다
멤브레인 LNG 화물창의 정적 강도평가를 위해 적용된 하중조건은 액체화물이 적재된 상태에서 발생하는 모든 하중조건을 기준을 작성되었다. 먼저 외력에 의해 발생하는 LNG 선박의 변형에 대한 하중조건은 Fig. 5에서와 같이 초기조건으로 선체 모델에서 발생하는 변위를 모두 포함하여 입력하였다.
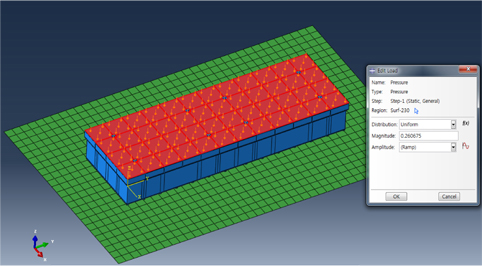
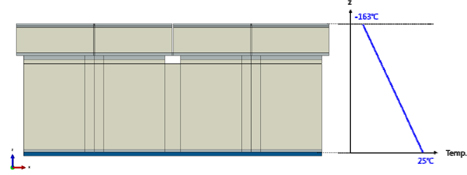
적재된 유체화물에 의한 정수압조건은 Fig. 9에서와 같이 액체화물에 의한 정수압이 화물창의 상부에서 균일하게 작용하도록 적용하였으며, 극저온 유체화물에 의한 열하중 조건은 Fig. 10에서와 같이 화물창과 접하는 상부 Plywood 부재가 −163℃ 이고 선체와 접하는 Mastic 부재가 25℃ 이며 화물창 내부에서의 온도분포는 선형적으로 분포한다고 가정하였다. Fig. 11은 열하중 조건이 적용된 상태에서 화물창의 온도분포를 보여주고 있다.
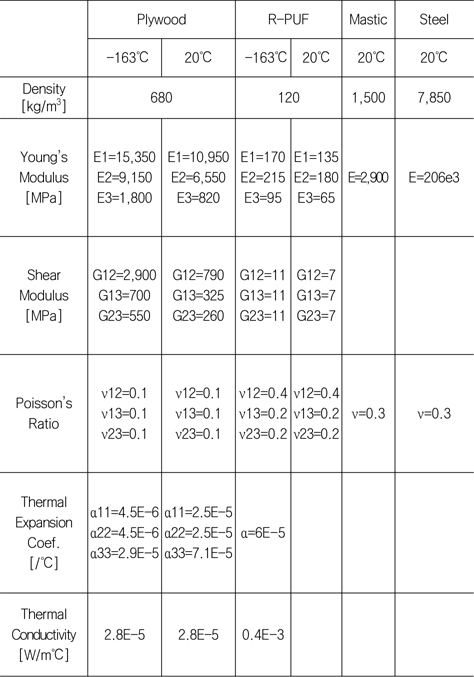
멤브레인 LNG 화물창의 유한요소 모델에 사용된 재료물성은 Table 1에서와 같이 Plywood, R-PUF 는 직교 이방성 재료로 가정하였으며, Mastic과 Steel은 등방성 재료로 가정하였다(Lee et al., 2007).
[Table 1] Material properties (Lee et al., 2007)
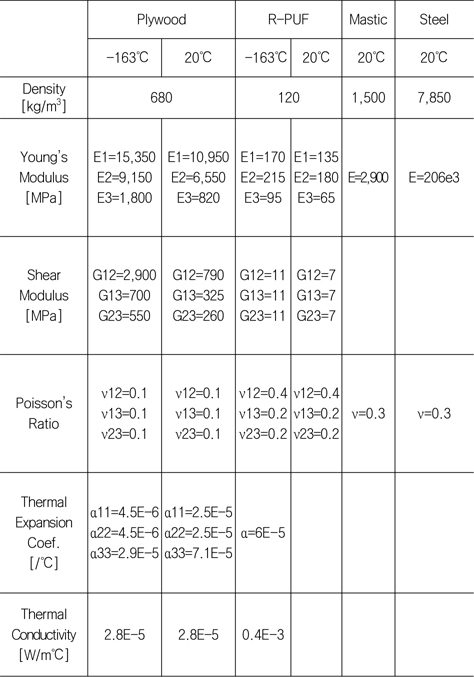
Material properties (Lee et al., 2007)
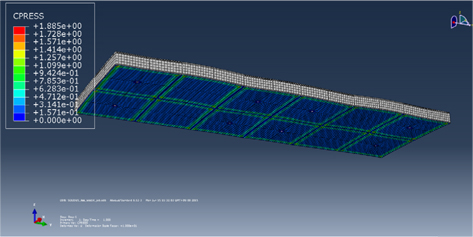
본 연구에서 검토 중인 LNG 화물창은 1차 방벽 과 2차 방벽이 접촉된 구조이며, 결속장치에 의해서 8개 지점이 고정된 형태로 구성되어 있다. 구조강도 평가 시 이를 단순화하기 위해서 자유도를 구속 기법을 적용하여 강도평가 모델을 작성하였다. 본 절에서는 앞 절에서 정의한 전역 해석 모델의 타당성을 1차적으로 검토하기 위해서, 자유도 구속으로 정의한 결속장치의 고정 유무와 방벽간의 접촉부에서 슬라이딩의 발생 여부를 검토하였다. Fig. 12와 Fig. 13은 1차와 2차 방벽에서 발생하는 접촉압력을 각각 보여주고 있다. 액체화물에 의한 압력이 방벽상부에 작용할 때, 결속 부에서는 고정된 형태로 변위가 발생하지 않는 것을 확인 할 수 있으며, 두 방벽의 경계부에서는 슬라이딩이 발생하여 접촉력이 발생하는 것을 확인 할 수 있다.
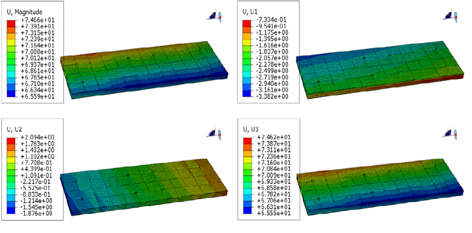
전역 해석 결과를 바탕으로 정적 하중이 화물창에 작용하였을 때 발생하는 최대 변형량 및 x, y, z 변위 성분들에 대한 변형량은 Fig. 14에서와 같다. 발생한 변형량은 약 80.5mm로서 z방향 변형이 크게 발생하였고 x, y 방향의 변위는 상대적으로 낮게 발생하였다.
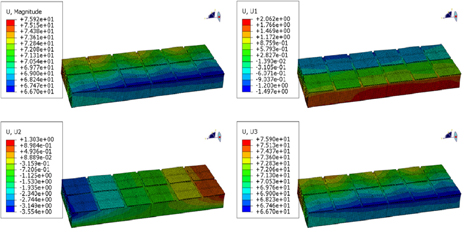
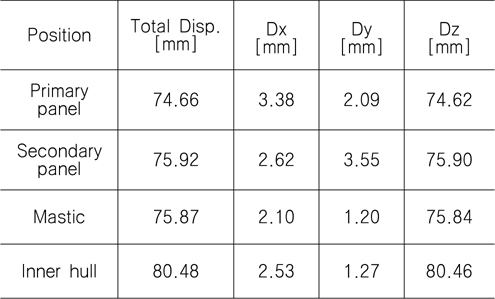
이는 Fig. 15에서와 같이 선체가 가지는 초기 변형량 때문에 발생한 것이며, 특히 수직방향의 변위가 크게 작용하고 있는 것을 알 수 있다. 또한 Fig. 16, Fig. 17에서와 같이 1차 방벽과 2차 방벽 에서 발생하는 최대 변형량은 각각 74.7mm, 75.9mm로서, 정수압에 의해 화물창이 수축하여 초기 선체 변형량에 비해 감소한 것을 알 수 있다. 화물창의 정적 강도평가를 통해 계산된 화물창의 각 부재별 최대 발생 변위는 Table 2에서와 같다.
[Table 2] Max. Displacement by global analysis of LNG CCS
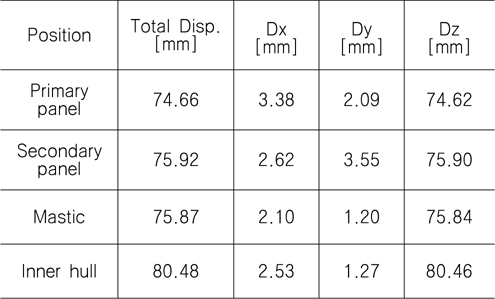
Max. Displacement by global analysis of LNG CCS
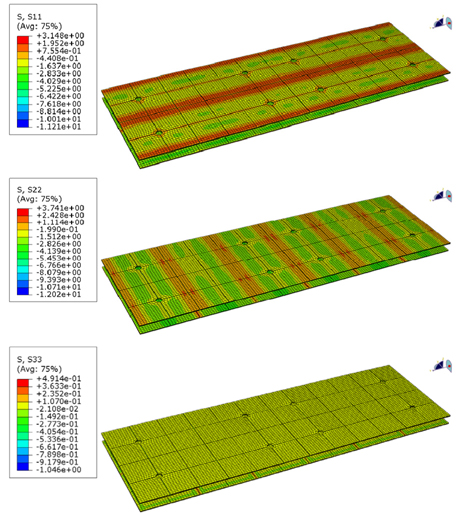
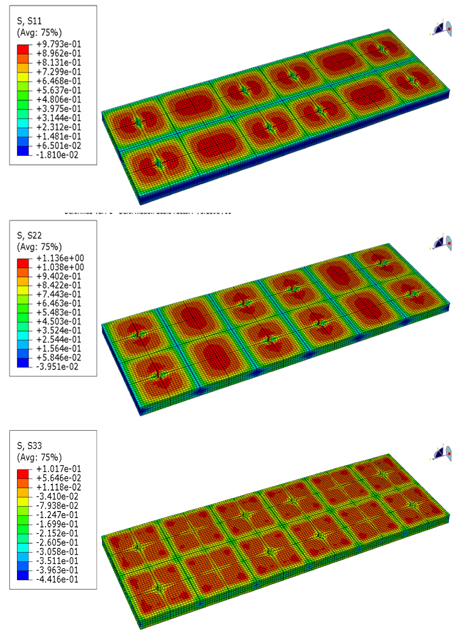
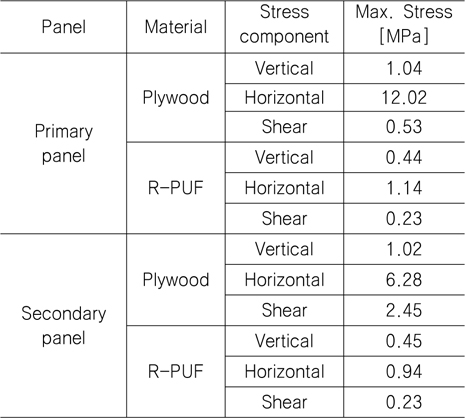
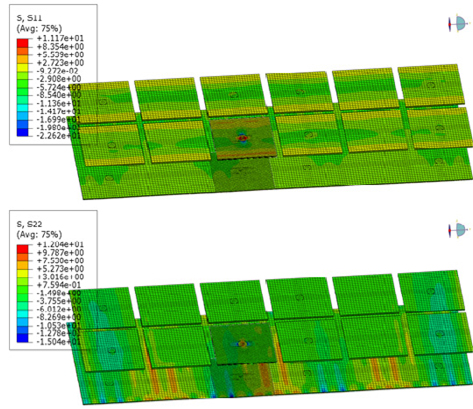
정적 강도평가 결과를 통해서 멤브레인 LNG 화물창의 각 부재에서 발생하는 응력을 각 부재 별로 검토하였다. Fig. 18은 Plywood에서 발생하는 응력을 성분 별로 도시한 것이며, Fig. 19는 R-PUF 부재에서 발생하는 응력 성분을 나타내고 있다. 그 결과 초기 선체 구조의 변형량 때문에 수직방향의 응력이 크게 발생하고 있고, 상대적으로 수평방향의 응력성분은 낮게 나타나는 것을 확인할 수 있다. 또한 2차 방벽에서 발생하는 응력 성분은 Fig. 20과 Fig. 21에서와 같이 수직 방향의 응력이 상대적으로 크게 발생하는 것을 알 수 있다. 각 부재별로 발생하는 최대응력을 정리하면 Table 3에서와 같으며, Plywood 부재의 경우 극저온 유체화물과 접하는 1차 방벽에서 응력이 상대적으로 크게 발생하는 것을 확인할 수 있다.
[Table 3] Max. Stress by global analysis of LNG CCS
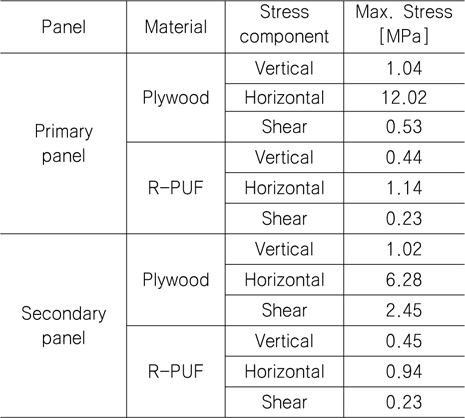
Max. Stress by global analysis of LNG CCS
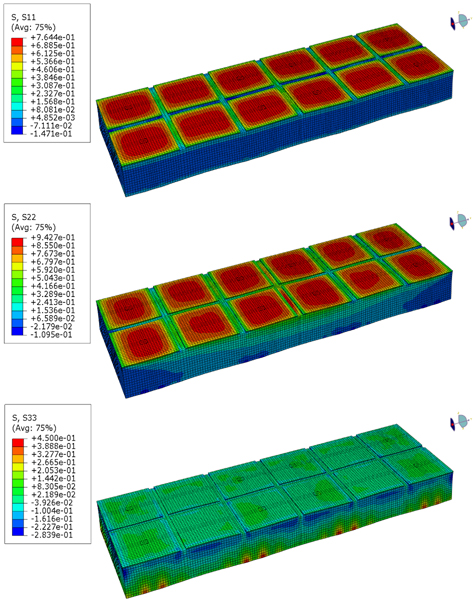
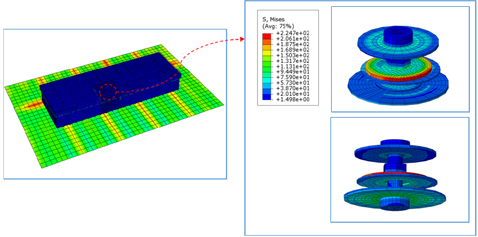
전역 해석과 같은 조건을 적용하여 결속장치의 강도를 평가하기 위한 국부 해석 모델을 Fig. 8에서와 같이 작성하여 강도 평가를 수행한 결과, 각 부재 별 발생하는 응력 성분에 대한 최대값은 거의 유사하게 평가가 되었으나, Fig. 22에서와 같이 결속장치가 부착된 2차 방벽의 수평 방향 응력성분이 약 12MPa로서 전역 해석 결과값의 약 2배정도 높게 발생하는 것을 확인할 수 있다. 이는 Fig. 6에서와 같이 결속장치가 2차 방벽에 부착될 경우, 해석 모델 상에서 단순화된 모델에 비해 기하학적 형상의 불연속이 발생하기 때문에 발생한 결과이고, 화물창에 작용하는 하중에 의해 발생하는 응력이 아니라 판단된다.
결속장치에 작용하는 응력은 Fig. 23에서와 같이 약 225MPa의 하중이 발생하는 것을 확인할 수 있으며, 특히 결속장치 중 Spring washer 부위에서 응력이 크게 발생하는 것을 확인 할 수 있다. 이는 유체화물에 의한 압력과 열하중이 CCS 에 작용할 경우 1차 방벽 및 2차방벽이 수축 변형을 하며 발생하는 Spring washer의 탄성변형 때문이라 판단된다.
본 연구는 −163℃의 극저온 상태의 단열 성능을 유지하며 구조안전성을 만족하기 위해 개발된 멤브레인형 LNG 화물창의 정적 구조강도를 평가 방법에 대해서 검토하고 그 결과를 통해 제시된 모델의 타당성을 검토하였다.
제시된 멤브레인형 화물창은 1차 및 2차의 두 개의 단열 방벽으로 구성되어 있으며, 액체화물의 유출을 방지하기 위하여 SUS(Stainless steel)재질의 멤브레인을 적용하고 있고, 1차 방벽은 결속장치에 의해서 구속되어 2차 방벽에 고정되어 있는 형태이다. 따라서 정적 강도평가 모델은 이러한 멤브레인 화물창의 특징을 반영하고 효율적인 해석을 위해 단순화된 전역 해석 모델을 제시하였으며, 해석 결과를 통해서 작용하는 하중에 대한 화물창의 타당성 있는 거동을 확인하였다. 또한, 1차 방벽 결속장치의 안전성을 판단하기 위해서 상세히 모델링된 국부 해석 모델로 구성하고 이를 전역 해석 모델과 연계하여 안전성을 평가하기 위한 모델을 제시하였다. 제시된 각 모델에는 온도하중, 정수압 조건 및 선체 변형을 반영하여 강도평가를 수행하여 제시된 평가모델을 적용하기 위한 타당성에 대해서 검토하였다.
추후 본 연구에서 제시된 모델을 기반으로 현재 개발 중인 멤브레인 화물창의 선급규정을 만족하기 위한 정적 강도평가 및 슬로싱 하중을 적용한 동적 강도평가에 적용할 예정이다.