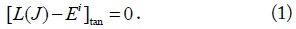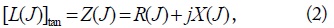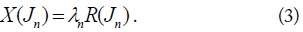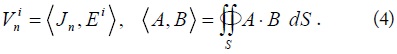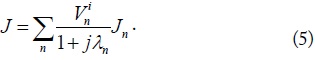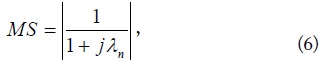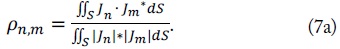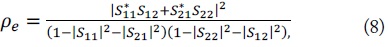Multi-input multi-output (MIMO) technology is widely considered to be a promising solution for telecommunication systems because of its many advantages. However, as mobile devices continue to become smaller because of the limitations of space and crosstalk (overlapping), the complexity of designing a multi-antenna system for use in compact devices increases. Among the approaches suggested for solving this problem, the characteristic mode analysis (CMA) is preferred because of its usefulness in intuitively understanding the antenna itself.

CMA is a theory of field analysis, which can describe the surface current in an arbitrary structure in terms of eigencurrents known as characteristic currents [1,2]. The far-field produced by each eigencurrent is orthogonal, and thus it can be used to determine the appropriate position for antennas when designing MIMO systems. Various approaches have been proposed to take advantage of the characteristic mode.

In [3], a systematic antenna placement procedure was demonstrated using CMA and the bandwidth potential concept. In [4], the position of dual antennas in a mobile terminal was determined based on CMA below the 1 GHz band. Further, in [5], a practical coupling structural concept, the Booster, was introduced to use CMA in a MIMO antenna design. [6] proposed the coupling structure for the current correlation coupling to be an exciter.

In this work, we propose the use of the factor known as the current correlation coefficient (C³) to explain the coupling effect between antennas. We validate this proposal through implementation. We choose a low band (below 1 GHz) for the purpose of simplicity, and the size of the device is 79 mm × 134 mm. Several parameters [7,8] have been proposed to calculate mode correlation. However, C³ is based on current, and thus it enables us to adopt an intuitive approach. It is also applicable when the structure is complex.

CMA was proposed and generalized by Garbacz and Turpin [1] and Harrington and Mautz [2]. After solving the method of moments (MoM), we obtain the Z-matrix, which is then decomposed into the eigenvalue and the eigenvector (eigenfunction or characteristic current). Solving the equation [Z][I] = [E] for the Z-matrix, [I], can be calculated as in [9].

Assuming the E-field Eⁱ to be incident to the arbitrary PEC (perfect electric conductor) surface S and using the conducting boundary condition, the following formula is obtained:

Physically, L(J) is the E-field, which is induced by J on the surface S. Eq. (1) has the dimension of impedance, so it can be expressed as follows:

where R(J) and X(J) are the real and the imaginary parts of the impedance operator, respectively. The characteristic currents are derived from Eq. (3) as a form of the eigenfunction J_n.

In Eq. (3), λ_n and J_n are the eigenvalue and the characteristic current of the n_th mode, respectively.

The modal coefficient can also be derived, assuming that the total current is expressed by a linear combination of the characteristic currents. Therefore,

Applying all the above mentioned results, we can express the total current as follows:

The physical meaning of Eq. (5) is that the total current J can be composed by the linear combination of the characteristic current J_n, the coefficient of which is determined by and λ_n. is the correlation between Eⁱ and J_n, where λ_n is expressed as the amount of reactive energy of the n_th mode. In particular, λ_n goes to 0 when the mode reaches the resonance frequency. The modal significance (MS) is defined as

which denotes how well the mode radiates at a particular frequency. As the MS increases to 1, the mode radiates more efficiently.

In practical terms, we require an additional structure to use the specific mode we desire. Two potential approaches are available. First, the mobile terminal itself can be used as an antenna with an electrically small coupling structure called the Booster. The second approach involves adding an antenna onto the ground plane. In the second case, we need to focus on the coupling problem, S₂₁, between the radiators. However, when we add an extra coupler, it changes its own characteristic mode prior to addition.

To make better use of CMA in the design process for MIMO systems, we propose a practical parameter called C³ as follows:

Then, it is discretized as follows:

where each J is the characteristic current of the n_th or m_th mode defined at mesh p (Fig. 1).

C³ has its own physical meaning and has a normalized correlation between the arbitrary characteristic currents (Fig. 2).

Therefore, we can use C³ in both cases for a more intuitive approach.

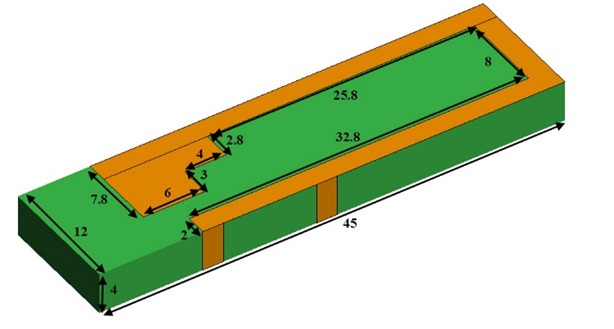
The size of the ground structure is 134 mm × 79 mm, and it is composed of PEC and FR4 (ϵ_r = 4.6). We choose a band near 800 MHz, which is the low band of the DMC project.

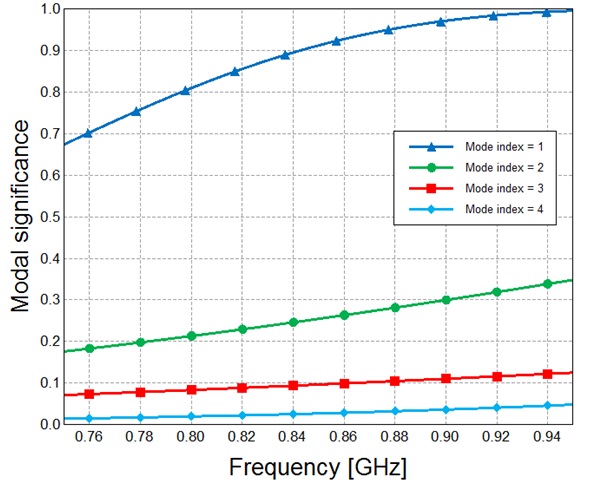
Considering the eigenvalues (Fig. 3) of each mode of the structure, we choose mode 1, which has a higher MS than the other modes. Therefore, mode 1 is the most efficient mode below 1 GHz. Mode 1 has a longitudinal current distribution shape. With this structure and C³, we can evaluate each design method numerically.

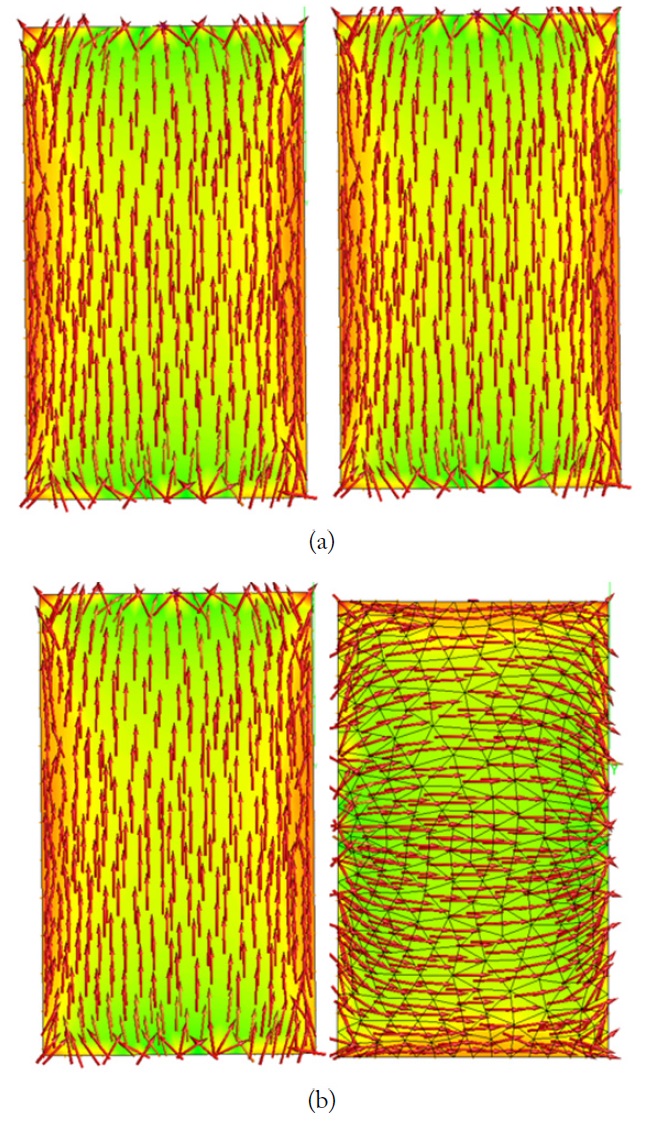
The Booster is an electrically small coupler used to excite the specific mode we desire. It has a relatively small size compared with the structure. Therefore, whether it is attached or not, no significant change is observed in the characteristic current distribution of the structure (Fig. 4). When the Booster structure is placed in the correct position, we can excite the mode we targeted without disturbing its own characteristic current distribution.

Among all the proposed structures, we choose a simple cuboid structure [5] to verify the usefulness of the C³.

To validate this method, we change the position of the Booster along the short edge of the ground plane and then check the C³ of the modified structure. Table 1 presents the results for the different positions, and we use C³ to confirm that no meaningful change occurs in the distribution because of the change in location. In other words, we have a greater degree of freedom when using the Booster structure to design the ground radiating antenna.

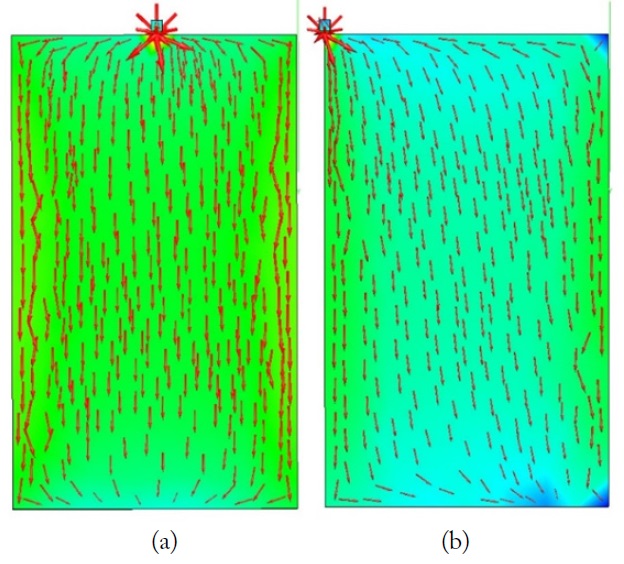
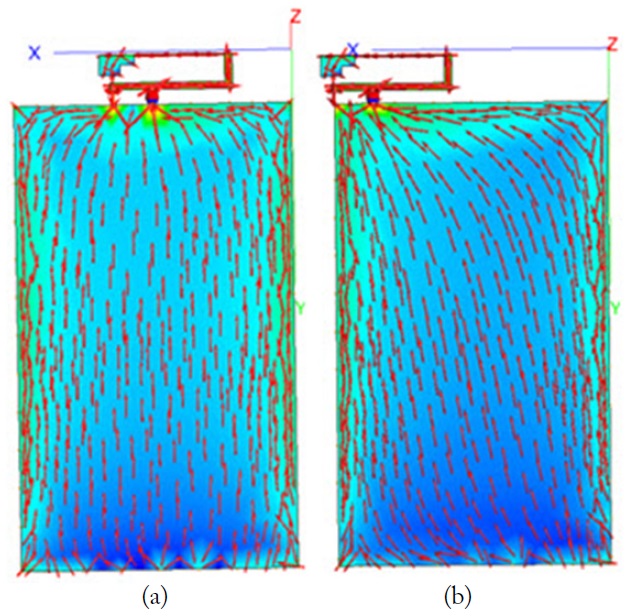
The radiator has its own radiating structure without a ground plane. We use the same procedure (Fig. 5) to observe the C³ value depending on its position. Unlike the Booster case, the radiator exhibits significant changes with the change in location (Table 2).

The results indicate that the degree of freedom of the design can be reduced when we use a radiating structure to excite the mode we want.

CMA appears to lose its advantage when the structure is modified because the outcome of the analysis can also be changed. Thus, using the radiator as a coupler for the specific mode can be disadvantageous in the design process.

The radiator can be affected by the ground plane and also by other radiators. Using C³, we can explain its coupling between radiators in a MIMO system on the same ground plane.

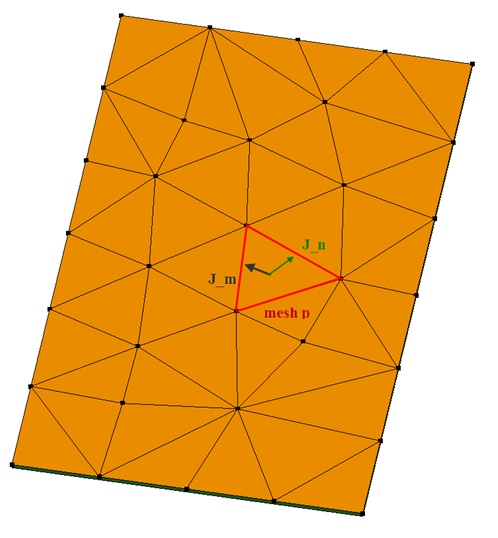
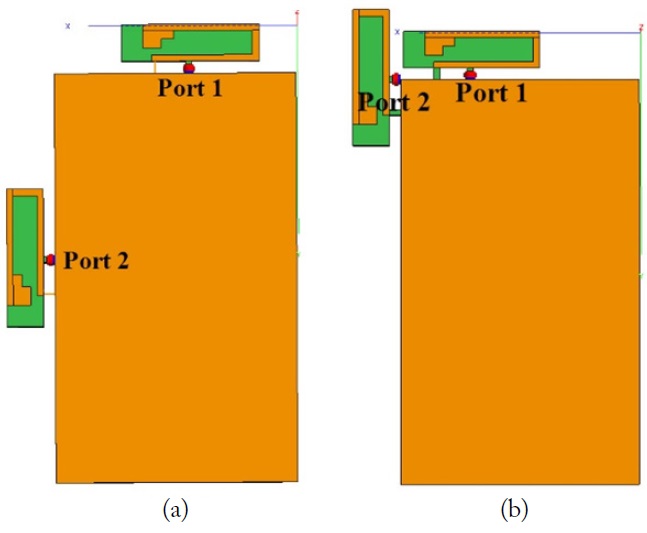
When considering the coupling between several antennas mounted on the same ground plane, C³ can also be a useful tool for explaining the phenomenon. If the current distribution produced by an antenna is similar to that produced by the others, then it can appear as the coupling effect. To validate this finding, we locate dual antennas (Fig. 6) located in the corners (Corner model in Fig. 7(b)), or middle edges (Middle model in Fig. 7(a)) of the ground plane and compare their coupling status. The dominant mode distributions produced by each port and the related ports are illustrated in Fig. 8.

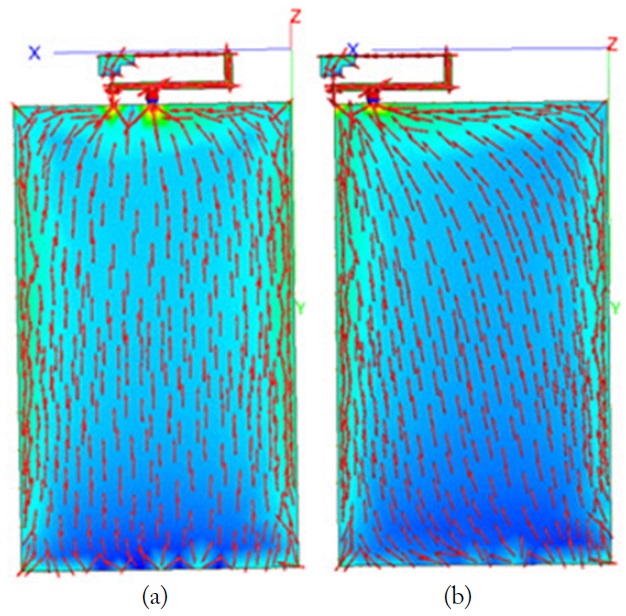
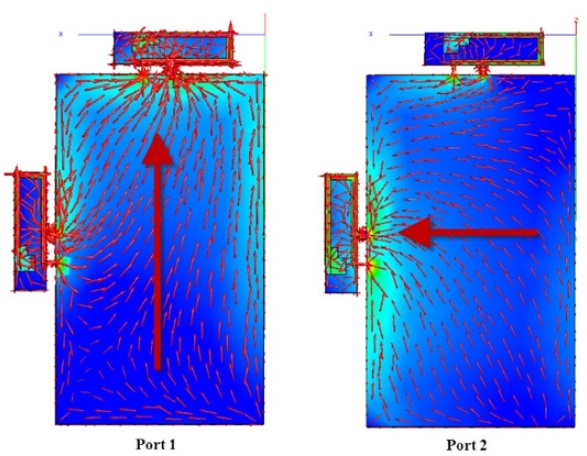
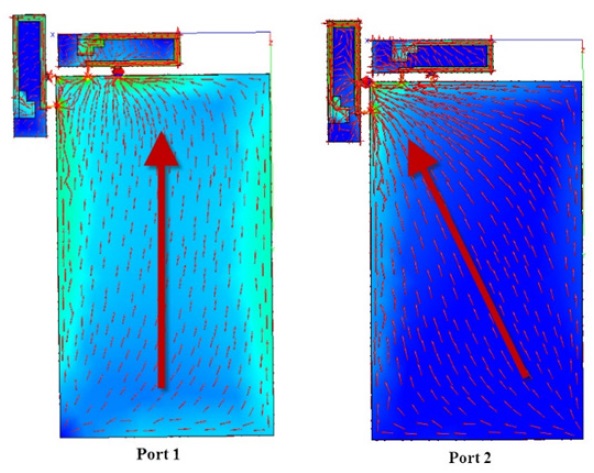
According to the results (Tables 3 and 4), a correlation is observed between ports 1 and 2 of the Corner model. The Middle model has a relatively smaller amount of correlation current distribution produced by ports 1 and 2 than the Corner model. (Tables 3 and 4) present the current correlation between the characteristic currents. The Middle model has a relatively smaller C³ than the Corner model. Therefore, the Corner model has more “correlated” current distributions than the Middle model. Accordingly, the Corner model has more coupling among the antennas.

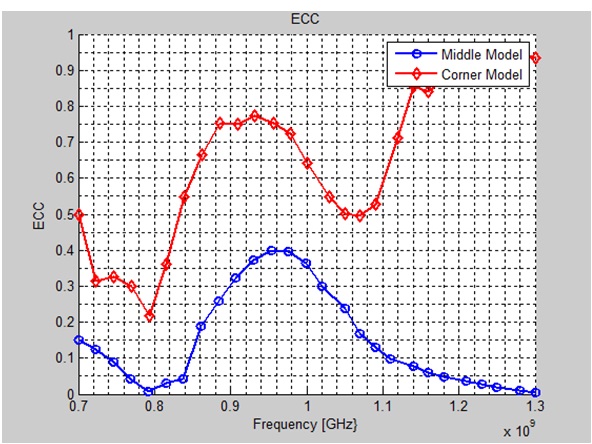
The envelope correlation coefficient (ECC) is the parameter that can estimate the performance of a MIMO system; a smaller ECC indicates better performance. The ECC between two antennas using the S-parameter is proposed in [10] as

and we adopt this approach as a crosscheck factor.

The result of the ECC is calculated (Fig. 9). Clearly, the trace of the ECC of the Corner model is larger than that of the Middle model. The main reason for this result is the coupling between the antennas. Thus, we prove that the result of the C³ coincides with the ECC value near 800 MHz.

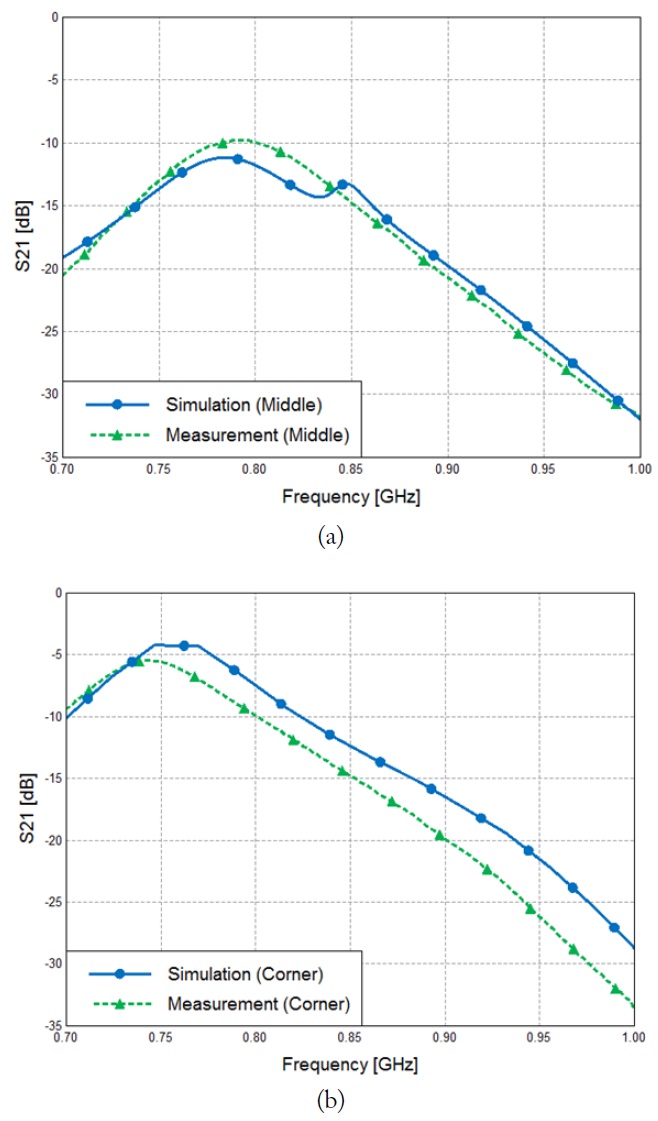
To validate the theory, an experiment is conducted using the Corner model and the Middle model as shown in Fig. 10. In the simulation, a MoM-based EM simulator called FEKO is used.

Fig. 11 shows the coupling, S₂₁, between the antennas in each model. Each model has its own f_res (795 MHz for the Middle model and 785 MHz for the Corner model).

Moreover, the current distributions of the Middle model are more orthogonal than those of the Corner model (Figs. 12 and 13).

Therefore, we are able to compare the coupling of the Middle model and the Corner model (–10 dB and –5 dB, respectively). We verify that the Middle model has a lower coupling tendency than the Corner model, thus validating the C³ results obtained prior to the experiment.

In this paper, we proposed the usefulness of the C³ factor and applied it in several design cases.

Two main approaches were used, namely, using the Booster and using a radiator. When using the Booster structure, which is electrically small whether it is attached or not, no significant change was observed. However, when using a radiator, which has an electrically large structure, a significant change in the ground plane’s CMA property was observed. Based on CMA, the Booster structure is more useful than a radiator in exciting a specific mode.

We also considered the coupling problem between dual radiators mounted on the same ground plane. Each radiator produces its own mode current. Therefore, we can compare the correlation to explain the coupling effect and validate this finding with other parameters (e.g., ECC and S-parameter). Future works can examine more than dual antennas on the same ground plane and/or use C³ in the near field.