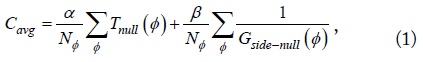A controlled reception pattern antenna (CRPA) array is widely used for a global positioning system (GPS) in various mobile applications, such as ground vehicles, ships, and aircraft. These applications adopt the CRPA array to suppress interference by forming a pattern null to the direction of an interference source in accordance with array weights iteratively updated by a space–time adaptive processing (STAP) algorithm. Although this iterative process performs well in a stationary system, the process is known to be less functional in a mobile environment because of the fast-varying direction of interference. For this reason, the null steering time has become an emerging consideration in mobile CRPA systems. However, only a few studies have reported on reducing the null steering time by developing a fast adaptive algorithm from a signal processing perspective [1–6].
This paper proposes an optimum array configuration to improve the null steering time for mobile CRPA systems. The proposed array is composed of nine uniformly distributed auxiliary elements with a reference element at the center of the array. The array radius is adjusted to optimize the null steering time, and the vertical placement of the center element is varied to suppress undesired side nulls in the upper hemisphere. Adaptive array patterns are computed using a microstrip patch antenna from Amotech [7], and their array weights are obtained from a constrained least mean square (LMS) algorithm [8]. The suitability of the proposed array is evaluated by comparing its null steering performance with a planar arrangement with the same number of elements. The results demonstrate that the steering time can be significantly improved with raised side-null gain by adjusting the array radius of the auxiliary element and the vertical placement of the center element.
II. PROPOSED ARRAY CONFIGURATION
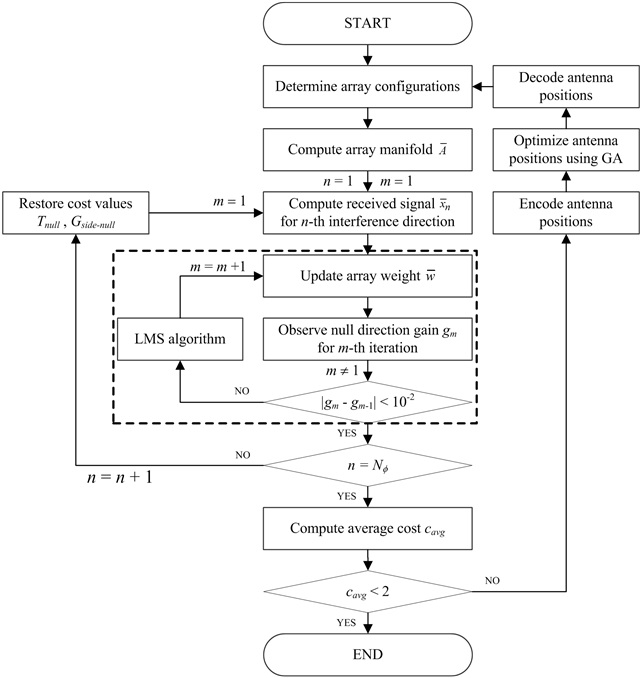
Fig. 1 presents a flowchart of our optimization process using a genetic algorithm (GA). The process is adopted to determine the optimum array radius and vertical placement of the center element in conjunction with the LMS algorithm for reduced null steering time. The null steering time is defined as the number of iterations to fully mitigate the effect of interference on the LMS algorithm. The process begins with determining an array configuration to compute an array manifold composed of steering vectors for all angles of elevation (
where
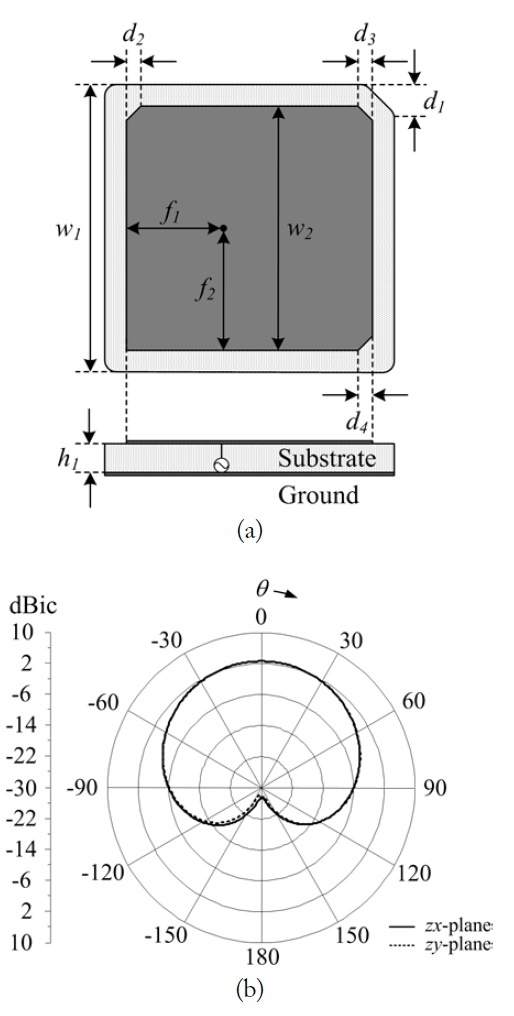
Fig. 2(a) illustrates the geometry of a microstrip patch antenna (Amotech Model B25-2D02753-STD70) that is applied to our process as an individual array element [7]. The antenna structure is printed on a ceramic substrate (
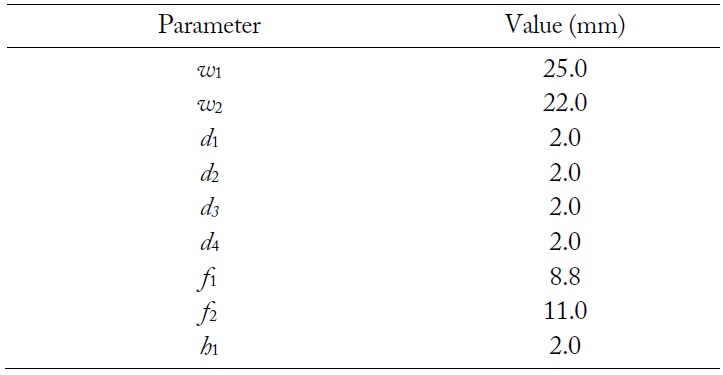
[Table 1.] Parameters of the array element
Parameters of the array element
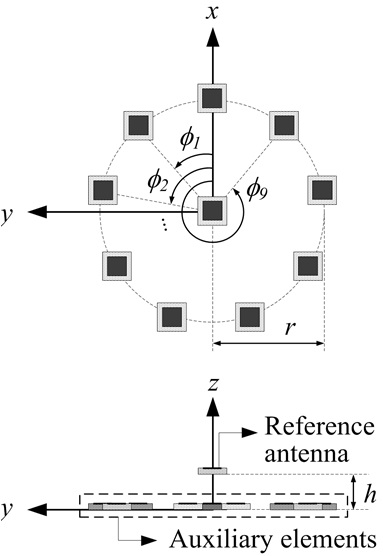
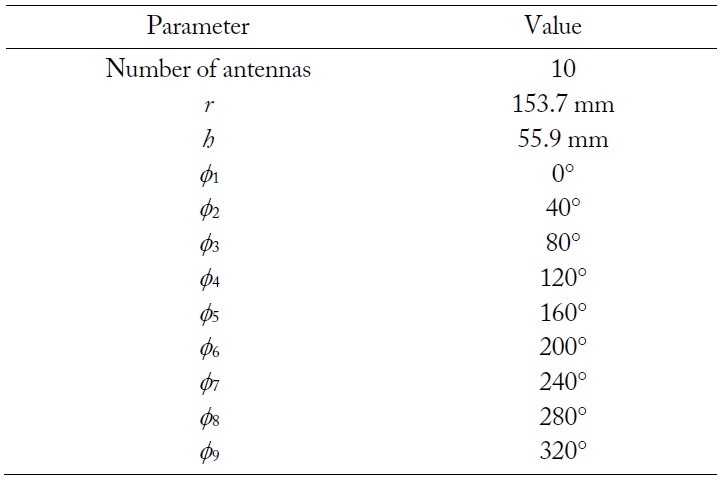
Fig. 3 shows the proposed array configuration that consists of nine auxiliary elements placed in a circular array and a single reference element at the center. The positions of the auxiliary element are determined by the array radius (
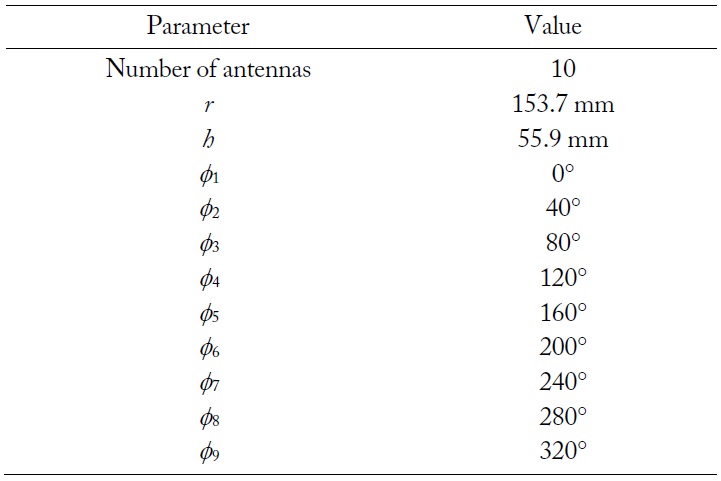
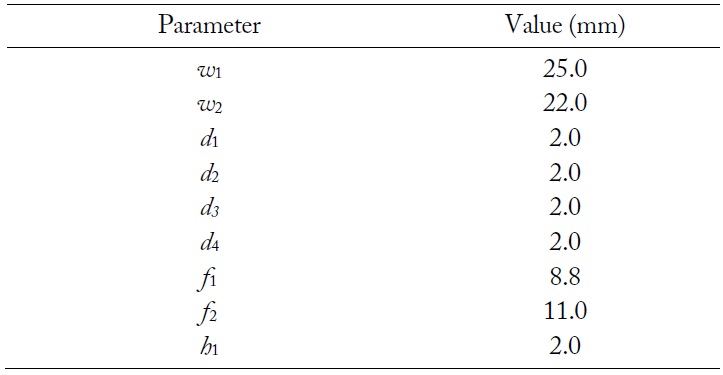
Table 2 presents the optimized values of the proposed array configuration. The array has a large array aperture with an interelement spacing of about 105 mm, and the center element is placed at
[Table 2.] Parameters of the proposed array element
Parameters of the proposed array element
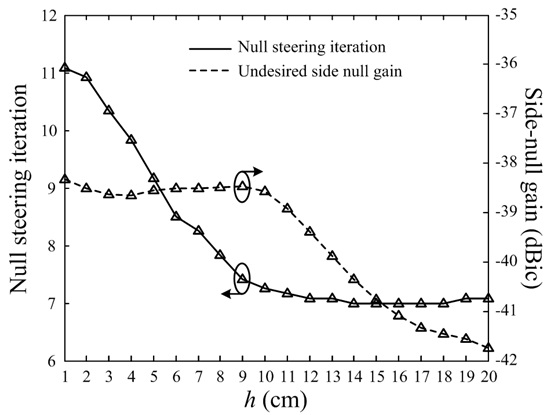
Fig. 4 demonstrates the effectiveness of placing the center reference antenna above the auxiliary antennas using the parameter
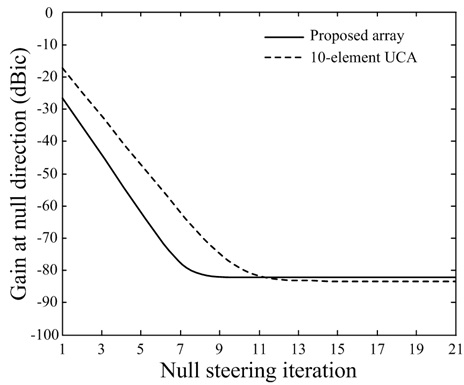
Fig. 5 presents the comparison of gain variations in the direction of interference according to the null steering iterations between the proposed array and a 10-element uniform circular array (UCA). The solid line illustrates the variation of array gains in the interference direction for the proposed array configuration, and the dashed line presents the variation of the UCA. We can verify that the null steering time can be more effectively reduced by placing the reference element at the center; for example, the array gain at the interference direction decreases by 15.5 dB compared with the UCA in the seventh iteration. In addition, the proposed array requires only 7 iterations to achieve a null direction gain of –80 dBic, whereas the UCA takes 11 iterations. This improvement becomes more significant in mobile environments, e.g., aircraft and missiles, because these applications require the processing time of less than tens of microseconds.
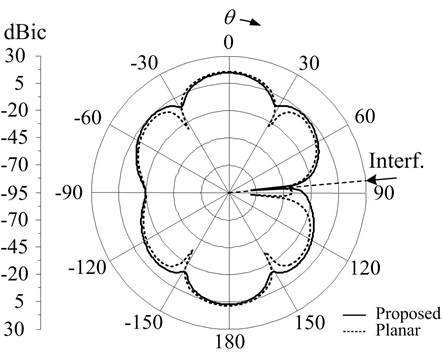
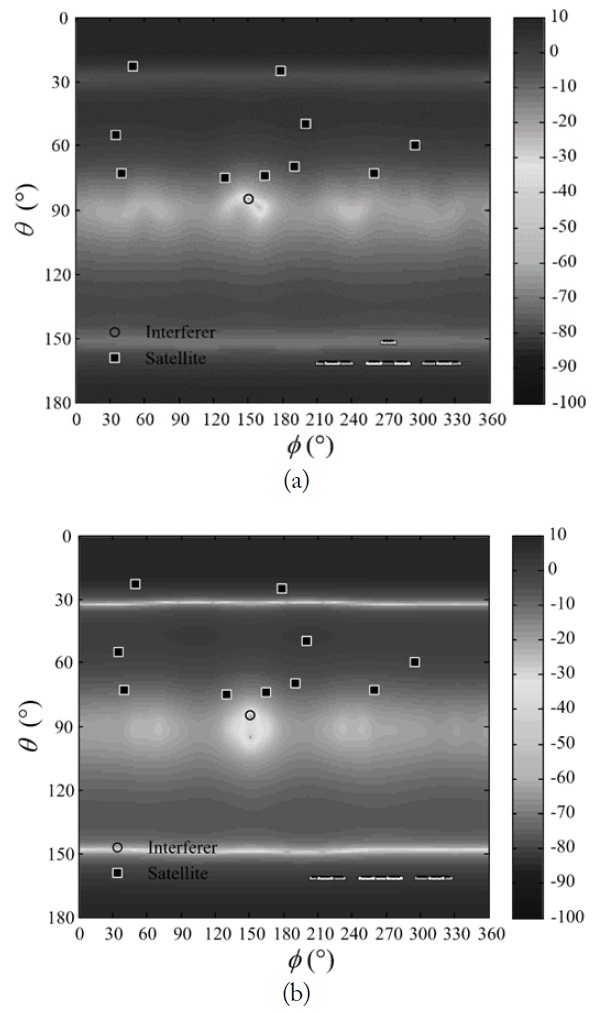
Another advantage of using the proposed array can be found in Fig. 6, which shows the comparison of the array patterns after the null steering process for an interference source placed at
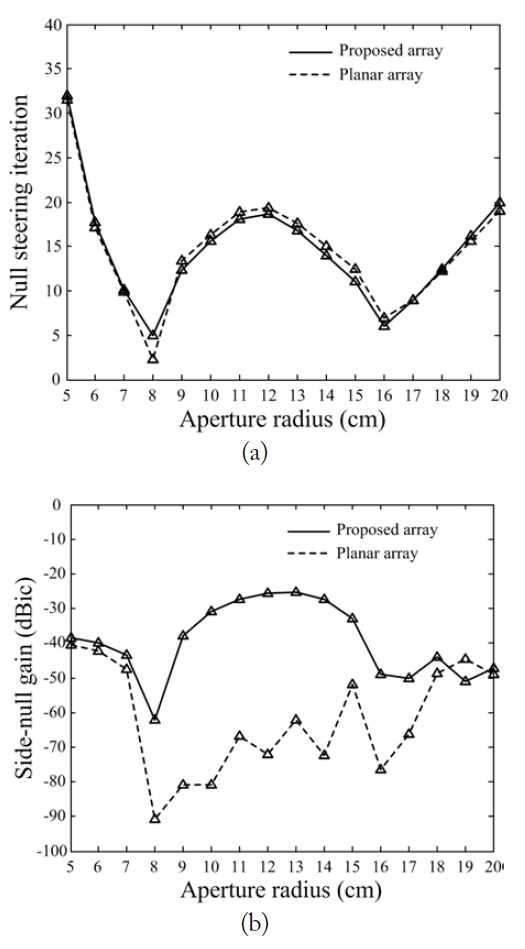
The proposed array configuration is then evaluated by varying the aperture radius from 5 cm to 20 cm as shown in Fig. 7(a) and (b). The solid line indicates the proposed array configuration, and the dashed line presents the planar arrangement used in Fig. 6(b). Both configurations show a similar trend for the null steering time, but they differ from each other in the sidenull gain because of the vertical placement. This analysis indicates that the null steering time is dependent on the array radius. Moreover, it supports the results in Fig. 6, which shows the variations of the side nulls according to the vertical placement of the center element. To further examine the importance of this vertical placement, the null steering performances are evaluated by adjusting the values of
We investigated an optimum array configuration to improve the null steering time for CRPA systems. The proposed array was composed of nine auxiliary elements arranged in a circular array and a single reference element, and its design parameters, such as the array radius and the vertical placement, were optimized by the GA. The null steering time and the side-null gain of the optimized array were then calculated in conjunction with the constrained LMS algorithm for evaluation. We verified that the reduced null steering time was suitable for fast interference mitigation and that the side-null gains could be increased by about 37.9 dB with the optimized vertical placement. This finding demonstrates that the proposed array is suitable for use in a mobile environment to achieve fast interference suppression without significant side nulls in satellite directions.