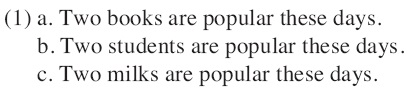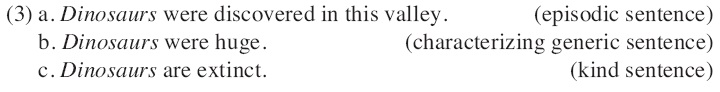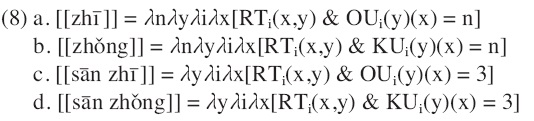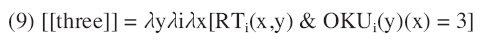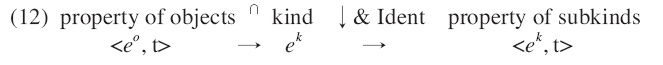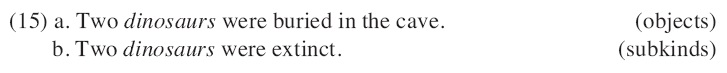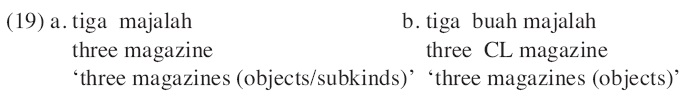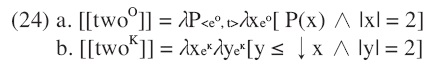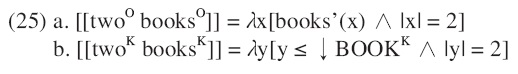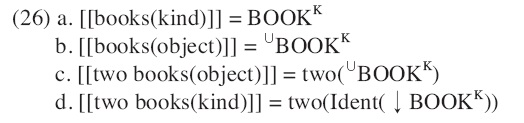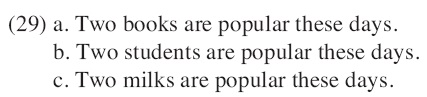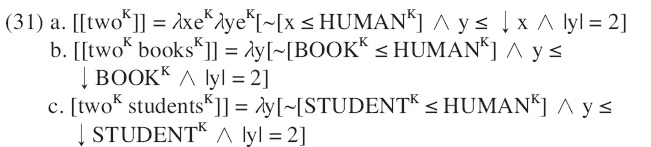Since Carlson (1977)’s seminal work, genericity has been one of the topics that are widely discussed in semantics. Although generic readings are conveyed through diverse forms of noun phrases (NPs), research has centered on characterizing generic readings of bare plurals. NPs with (in)definite determiners, demonstratives, or numerals have not drawn much attention. Kind-denoting interpretations are also treated as a secondary topic, compared with characterizing generic ones. This study will address a topic which is worth getting more academic attention: kind readings of NPs with numerals.

NPs with numerals show different patterns in their interpretations, occurring with predicates which take either an object or a kind as their argument.

The sentences in (1) are distinct only in the selection of the nouns in their subject positions, and the predicate be popular applies to either objects (including individuals) or kinds. (1a) asserts the popularity of two  individual books or two titles of books, having an ambiguity between the object and the kind readings. However, (1b) is concerned about the popularity of two individual students while (1c) focuses on the popularity of two kinds of milk. The distinction in the interpretations is more sharpened when objects or kinds are specified as in (2).

Two books is specified as two copies of John’s books in (2a) and two titles Book A and Book B in (2a’). Either of the sentences sounds natural, which supports the ambiguity of two books between the object and the kind readings. In contrast, the specification of kinds is quite awkward with two students as in (2b’) and that of objects with two milks as in (2c). Because the syntactic structure and the selection of the predicate are consistent, the different interpretations shown in (1) and (2) hinge on the semantics of the subject NPs.

To account for different preferences between object and kind readings, I will briefly summarize diverse categories of readings in generic sentences, giving a focus on kind readings of numeral NPs. I will critically review previous analyses on kind readings of numeral NPs and argue that none of the analyses provide satisfactory accounts for the different preferences. I will revise an interpretation domain for the interrelatedness of an object domain and a kind domain and propose a lexical restriction on the semantics of numerals.

Sentences may assert specific events or states that are restricted by time and space. For instance, (3a) asserts the event of discovering dinosaurs specified by the time of the past tense and the place referred to by this valley.

(3a) is called an ‘episodic’ sentence due to its specificity, and dinosaurs refers to a set of specific dinosaurs. In contrast with (3a), when

bare plurals occur with a predicate of general property, they are conducive to generic readings. Dinosaurs in (3b) is not interpreted as a set of specific dinosaurs; rather, it is interpreted as dinosaurs in general, which  are asserted to be huge.1 This class of genericity is called ‘a characterizing generic’, which is to report a regularity that summarizes a set of particular episodes or facts.2 Genericity covers not only a characterizing generic but also ‘a direct kind predication,’ which involves a special type of entity ‘kind.’ (3c) is not construed that dinosaurs in general are extinct; rather, it asserts that the kind or species of dinosaur as a whole is extinct. Hence, dinosaurs in (3c) refers to a special entity of kind individual.

According to Krifka et al (1995), there are predicates which take only kind-referring terms in their argument positions. For example, the subject argument of die out and be extinct are filled only with kinds while invent and exterminate take only kinds as their objects. Others like be a mammal or be domesticated are preceded by either object- or kind-referring terms. This shows that the lexical properties of predicates play a crucial role in making kind sentences.

Kind-referring terms are understood to denote kind individuals that are generated from the maximal sets of entities. Whether they are of bare plural forms or singular NPs with the definite article, kind NPs denote unique individuals that are abstract away from objects. Occurring with the kind-taking predicate be extinct, both dinosaurs and the dinosaur refer to the unique entity of kind Dinosauria. The maximality of kinds does not allow countable readings. However, when kind NPs do not denote the whole species but subkinds of species, they behave like count nouns syntactically.

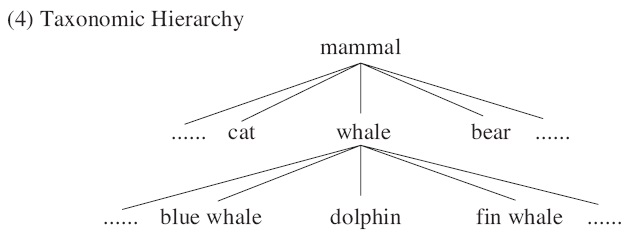
Here is a taxonomic hierarchy which shows that the species of whale is further divided into several subkinds such as blue whale, dolphin, fin whales, etc.

Just as individuals are summed to make a larger entity, subkinds are conflated into a higher entity of kind. Taking a number of subkinds in its denotation, the kind whale is countable in its subkind readings. According to Krifka et al (1995), it occurs with the indefinite article, numerals, demonstratives, or quantifiers as in (5).

All the NPs with whale in (5) do not refer to or quantify over the whole species Cetacea but subkinds such as blue whale, dolphin, fin whale, etc. These are called ‘taxonomic’ or ‘subkind’ readings.

Subkind readings are not limited to count nouns. Mass nouns occurring in a count noun context typically get taxonomic readings.

Two red wines in (6) does not denote a specific quantity of wine but subkinds of wine. Although diverse categories of nouns induce subkind readings, Krifka et al (1995) add that nouns associated with no species are hard to get subkind readings. For instance, the sentence a dodo is extinct sounds quite awkward. The singular indefinite a dodo cannot refer to the whole kind but only to a subkind. However, the kind dodo does not have taxonomic entities in its denotation, which makes the sentence sound awkward.

1One of the important features of characterizing generics is that they admit exceptions in their denotations. The existence of some dinosaurs that were nothuge does not make a difference in the truth of (3b) as far as they make a miscellaneous set of entities.  2Characterizing generic sentences include generalizations over events as well as generalizations over objects as in (3b). For example, (i) conveys a habitual reading of John’s activity. (i) John smokes a cigar after dinner. (i) is not about one instance of John’s smoking a cigar. It is about John’s habit, which is a generalization over the events of John’s smoking after dinner. For more argument about the habitual readings of generics, see Krifka et al (1995) and Pelletier et al (1997).

To derive subkind readings, Krifka (1995) notes that kind terms and proper names show close similarities and argues that kind terms denote names of kind individuals. An interpretation domain is divided into two structures, one for objects and the other for kinds. The structure of kinds makes a taxonomic hierarchy as in (4). Krifka also discusses the fact that kinds are ontologically prior to objects because all languages which allow bare NPs use them to refer to kinds.

Krifka posits two functions to derive object and subkind readings: realization relation R and taxonomic relation T. In the intensional framework, R and T depend on a possible world i. Then, if k is a kind, λx.R_i(x,k) applies to objects of k in a world i and λx.T_i(x,k) applies to subkinds of k in a world i. RT is the union of these two relations: RT_i (x,y) = R_i(x,y) ∨ T_i (x,y).

Given the relations, Krifka argues that classifier and non-classifier languages show distinction in the interpretations of kind terms with numerals. In classifier languages, classifiers distinguish the selection of objects and kinds whereas in non-classifier languages numerals include unit readings which encompass both objects and kinds. For example, Chinese, a classifier language, adopts distinctive classifiers to deliver object or kind readings.

The classifier zhī is reserved for objects and zhǒng for kinds.

Krifka suggests two operators OU and KU for numeral readings. For each possible world, OU takes a kind and yields a measure function that measures the number of objects of that kind, and KU takes a kind and yields a measure function for the number of subkinds of that kind. Then, the classifiers zhī and zhǒng are construed as follows:

Taking a kind y in each possible world i, zhī yields objects x the number of which is specified by a numeral n, and zhǒng yields subkinds x the number of which is specified by the a numeral n. When they are combined with a numeral like sān, their respective interpretations are like the ones in (8c) and (8d).

Although the selection between objects and kinds is specified by classifiers in classifier languages, non-classifier languages cannot make use of this strategy. Hence, Krifka argues that measuring functions are incorporated in the semantics of numerals, which includes OKU, the union of OU and KU. For instance, the numeral three in English is assigned an interpretation like the following:

Since a non-classifier language like English does not have classifiers to encode the measuring functions, the semantics of numerals incorporates the conflated function OKU. Taking a kind y in each possible world, three yields either objects or subkinds of y which are numbered three.

Krifka’s argument for the distinctive semantics between classifier and non-classifier languages has inspired much following research. The notion of the measuring functions is also understood as useful to derive numeral readings. Despite these merits, his analysis does not have a clue for the different preferences of subkind readings between human and nonhuman nouns as pointed out in section 1. He postulates a taxonomic hierarchy which is not affected by semantic feature like humanness, andthus there is no theoretical ground to distinguish the kinds of book and student in numeral readings.

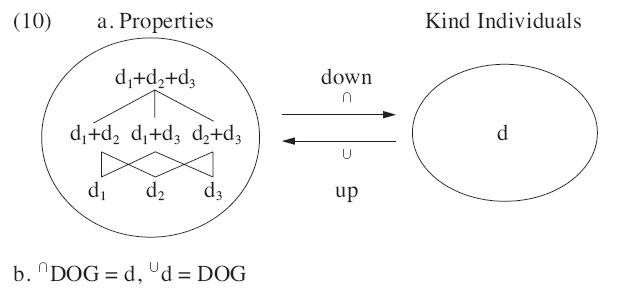
To account for kind readings cross-linguistically, Chierchia (1998) adopts a lattice-theoretic structure for the interpretation domain of individuals and kinds, following Link (1983) and Landman (1989).3 In their analysis, singular and plural entities are equally postulated as entities, which are defined by the join operation ‘+’ and the part-of relation ‘≤’ in a join semi-lattice structure. Suppose that a world w has only three individuals d₁, d₂, and d₃ for dogs . The singular noun dog denotes a set of atomic entities {d₁, d₂, d₃} while the plural noun dogs denotes a set of sums generated from the atoms by the join operation, i.e, {d₁+d₂, d₁+d₃, d₂+d₃, d₁+d₂+d₃} in this world.

Given the lattice structure of individuals, Chierchia argues that objects and kinds make separate structures and that they are mapped to each other by operators.4 The properties of the three dogs d₁, d₂, and d₃ in a world w make a lattice structure as in (10), and the kind dog d is posited as an individual. The properties of the dogs are mapped to the kind d by the down operator ‘^∩’, and the kind d is mapped to the dog properties by the up operator ‘^∪’.

In Chierchia’s analysis, kinds do not make a taxonomic hierarchy as in (4). Kinds are individuals that make a lattice structure and they are mapped to objects by the operators. Hence, kinds are not restricted to biological ones or ‘well-established’ ones. Chierchia argues that artifacts (like chairs or cars) or complex things (like intelligent students or spots of ink) may also make kinds as far as they show sufficiently regular behaviors. He further adds that what counts as kind is not set by grammar but by the shared knowledge of a community of speakers. Thus, the structure of kinds varies with the context to a certain degree and remains somewhat vague. Chierchia concerns himself with the semantics of characterizing generics, which is discussed to be derived from kinds. Hence, the concept of kinds is broad enough to include all instances of characterizing generics.

Chierchia’s analysis provides a satisfactory account for the typological aspects of NPs. As for the current topic of subkind readings, kind entities are assumed to be determined by the shared knowledge of language users and may be affected by contexts. At first glance, this appears to leave room where human and nonhuman nouns are distinctively assigned kind entities. However, Chierchia claims that all lexical nouns are mapped to kinds and that complex nouns may or may not. Hence, his framework does not provide a structure in which human and nonhuman nouns have different biases towards subkind readings.

In the analyses of Krifka (1995) and Chierchia (1998), a single structure is postulated for kind entities although the shape of the structure is distinguished. Krifka’s structure is more oriented to the taxonomic hierarchy, and Chierchia’s to the lattice-theoretic structure. This leads to the difference that kind entities of Krifka’s analysis are defined narrowly to include natural kinds or well-established ones while those of Chierchia’s are broad enough to encompass all entities that are mapped to sums of objects.

Nomoto (2010) follows the previous analyses in that individuals consist of two basic sorts, i.e., object and kind individuals, which are distinctly typed.5 He also adopts a lattice-theoretic domain of individuals in the sense of Link (1983) & Landman (1989). What deviates from the earlier approaches is that he posits two structures for kinds: a taxonomic one and a lattice-theoretic one. Following Dayal (2004), Nomoto argues that a taxonomic hierarchy is a list of names that denote natural kinds as exemplified in (4). Kinds used in generic sentences are not restricted to natural kinds, so a taxonomic hierarchy is just part of the kind structure.

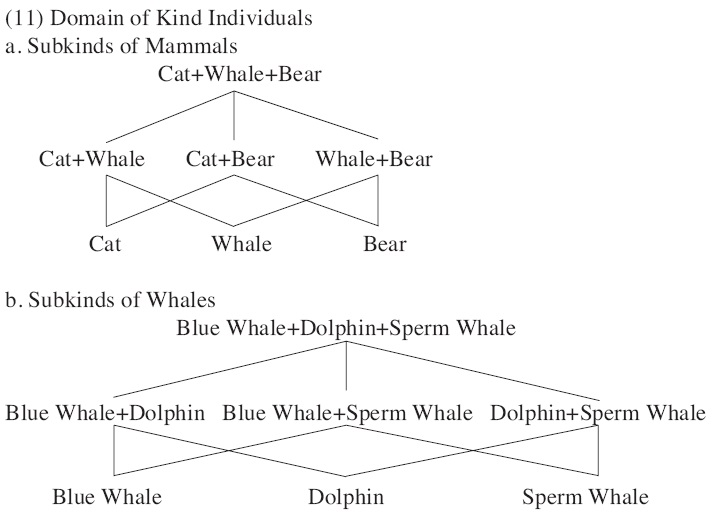
Kinds are individuals like objects. They are only distinguished in their types. Hence, kinds also constitute a lattice-theoretic structure like objects. For instance, the kinds and subkinds of mammals and whales are represented as in (11).

Nomoto argues that an atomic kind individual like whale is a group derived from its subkinds by the group formation function ‘↑’.6 In a world w, where there only three kinds of whales such as blue whales, dolphins, and sperm whales, these three kinds make a lattice structure as in (11b). The supremum of these three kinds, i.e. Blue Whale+Dolphin+Sperm Whale, is mapped to a group ↑(Blue Whale+Dolphin+Sperm Whale), which is identified as the kind whale. Then, the kind whale is again makes a lattice structure with other mammals as in (11a). In this domain, a taxonomic hierarchy is understood as the structure consisting of group entities of kinds without including sums of kinds.

Nomoto further argues that subkind readings are derived by the application of the member specification function ‘↓’ and the type-shifting function ‘Ident.’7

According to Chierchia (1998), the property of objects is mapped to a kind individual by ^∩. Since this kind is assumed to be a group of subkinds in Nomoto’s analysis, ↓ is needed to map it to a sum of its subkinds. Finally, Ident takes a sum of subkinds and yields a set of subsums. Bare nouns are type-shifted to derive subkind readings.

A type-shifted subkind reading is exemplified by whales as in (13).

The kind whale is a group of the three kinds of whales as in (13a). The subkind reading of whales is type-shifted as in (13b). First, ↓ applies to the group to yield a sum of the three species. Then, Ident turns a sum of the species into a set of subsums. In this set, the subkind reading of two whales takes subsums, the number of which is restricted to two atoms.

In the lattice-theoretic domain, where kinds and subkinds are related with the group formation function, the semantics of numerals is uniformly defined regardless of whether they combine with objects or kinds. After being type-shifted, bare nouns in subkind readings denote a set of sums just like bare nouns in object readings. Hence, the semantics of numerals simply restricts the number of atoms in the sums that are selected.

In spite of the convincing argument for the group denotations of kinds, Nomoto’s analysis is not equipped with a mechanism for the distinct preferences of subkind readings. Although a nonhuman NP like two books is freely construed as denoting subkinds, a human NP like two students is restricted to an object reading. In Nomoto’s analysis, ↓ and Ident equally apply to both human and nonhuman NPs with numerals.

When the kind book is member-specified and makes a set of sums by the functions, it is mapped to a sum of subkind like Book A and Book B. Likewise, since taxonomic kinds are the results of group formation of subkinds, human kinds like student are also related with their subkinds by the functions. When the type-shifting procedure applies to the kind student, it yields a set of subkinds of students such as elementary school students and middle school students. Hence, two students is wrongly analyzed as having a subkind reading in Nomoto’s analysis.

3Although Chierchia (1998) follows Link (1983), he does not accept nonatomic properties of materials for mass nouns. Chierchia assumes that mass nouns are plural by themselves.  4Chierchia (1998) assumes that properties and kinds are of different types. Properties are of type > and kinds of type e. Hence, they do not make a single structure.  5Object individuals are of type eo, and their properties . Kind individuals are of type ek, and their properties are naturally of type . The different types of objects and kinds contribute to make two distinct structures of objects and kinds.  6Link (1984) and Landman (1989) argue that higher entities of ‘groups’ are needed in the domain to deal with the interpretations of collection terms like committee. Collection terms have ambivalent properties in that they are singular but have plural members internally. Ordinary atoms are called ‘pure’ atoms, and groups, which are atoms generated from a sum of members, are called ‘impure’ atoms. To assign interrelations between pure and impure atoms, the group formation function ↑ is defined to map a sum to a group while the member specification function ↓ maps a group to a sum of its members.  7The formal definition of ‘Ident’ is given by Partee (1987) as follows: Ident := λxλy[y≤x] The function Ident takes an individual (or sum) and yields a set of subsums of the individual.

For the proper treatment of subkind readings, we will consider howsubkind readings are affected in sentences. First, as noted in the previous analyses, the lexical properties of predicates are crucial in determining kind or subkind readings.

The whole species of a kind cannot be buried in some place in most cases. Thus, be buried is a predicate that does not take a kind as its argument by its lexical property. The restriction of a kind reading also applies to a subkind reading, so two dinosaurs in (15a) is not construed as denoting two species of dinosaurs. On the other hand, be extinct is one of the representative predicates that select only kinds as their arguments. Individual objects cannot be extinct by nature. A kind only in the argument position means that an NP with a numeral leads to a subkind reading of the predicate. Hence, two dinosaurs in (15b) is naturally understood as two species of dinosaurs.

In addition to the lexical properties of predicates, I argue that those of nominal arguments also play a crucial part in determining subkind readings. As noted in section 1, not all nouns can make subkind denotations even in the cases that they occur with predicates with kind arguments.

Be popular is a predicate that applies to either objects or kinds. Individual objects (including people) may be popular to a group of people or kinds may be popular to general population. Given the ambiguity of the predicate, all the sentences in (16) are expected to have two interpretations, one for objects and the other for kinds. However, only (16a) is ambiguous as paraphrased above. Two students is construed as denoting only specific individuals such as John and Bill while two milks is confined to a subkind reading as exemplified. In view of the fact that both book and student are count nouns, the countability of the nouns does not hinge in their interpretations. When countability is excluded, the semantic features of the nouns like humanness may be considered as a factor in determining the sentence interpretations.

A scrutiny with more examples shows that the semantic feature of nouns indeed functions as a decisive factor in the selection of object and subkind readings.

Just as be popular applies to either objects or kinds, the predicate dislike may also apply to both categories of entities. People dislike specific objects or species in general. All the objects in (17) are paraphrased with subkind entities of the NPs. If the object NPs allow subkind readings, the paraphrased sentences in (17) should sound natural. However, the sentences show different degrees of acceptability. The human NP in (17a) sounds quite awkward whether it is paraphrased as denoting subkinds divided by school grades or school names. The primary reading of two dogs in (17b) is the object interpretation. However, its subkind reading is  not as awkward as two students. The other NPs in (17) are naturally construed as subkind entities. Notice that the nouns in (17) are deployed according to an animacy hierarchy.8 The human noun takes the highest position in the hierarchy, and the human-friendly animal dog takes a position higher than the other entities. Insect and flower are situated in lower places than human or dog although they are animate. Finally, the inanimate object book takes the lowest position. This means that the higher position the NP denotations take in the animacy hierarchy, the more likely they will have subkind readings. Therefore, it is concluded that both the lexical properties of predicates and nouns need to be considered in deriving subkind readings.

English is classified as a language which does not have classifiers in its grammar. Hence, subkind readings of NPs with numerals are affected only by the lexical properties of predicates and nouns. In contrast with non-classifier languages like English, classifier languages have further mechanisms that affect subkind readings, i.e., classifiers.9 Various language show different patterns of object and kind readings of numeral  NPs.

In Chinese, classifiers are mandatory to numeral NPs, so nouns cannot combine with numerals without the occurrence of a classifier. For numeral readings, distinct classifiers may be used to denote objects and kinds as discussed by Krifka (1995).

The classifier zhī is reserved only for objects while zhǒng is used to denote kinds. To reflect this interpretive distinctness, part of the semantics of classifiers in Chinese is to describe whether they apply to objects or kinds.

Unlike Chinese, classifiers in Malay yield only object readings. (cf. Nomoto 2010)

In contrast with the obligatory use of classifiers in Chinese, classifiers are optional in numeral NPs in Malay. Hence, two forms of NPs are available as in (19) to deliver numeral readings. Interestingly, numeral NPs without classifiers have an ambiguity between object and kind readings. The NP without the classifier buah in (19a) denotes either three specific magazines or three kinds of magazines. However, the occurrence of the classifier as in (19b) has a blocking effect of the subkind reading, so the NP refers only to three specific magazines. Thus, part of the semantics of classifiers in Malay is to restrict arguments to the object domain.

Although Korean is a classifier language where classifiers are optionally used in numeral NPs, subkind readings show a pattern that parallels with that of English. NPs that are highly ordered in the animacy hierarchy do not freely denote subkind readings while those in lower positions are easy to have subkind readings.

Chayk ‘book’ denotes inanimate objects, so it is situated in a lower position than other animate nouns. Haksayng ‘student’ refers to human entities, and thus it takes a higher position. Given the distinct order of the nouns in the animacy hierarchy, the NP in (20a) has an ambiguity between object and kind readings while the one in (20b) is restricted to an object reading. The distinctness exactly accords with the pattern in  English.

Subkind readings affected by the animacy hierarchy are also observed in Malay. (cf. Nomoto 2010)

As noted above, numeral NPs without classifiers are supposed to have subkind readings in Malay. However, nouns show different degrees of acceptability even in bare numeral structures. Nomoto observes that the ease of an object reading is higher in the following order: orang ‘person’ (human) > kucing ‘cat’ (nonhuman animal) > bunga ‘flower’ (plant). In other words, nouns of high animacy are more restricted in their subkind readings even when they do not occur with classifiers.

Chinese, Malay, and Korean are all classifier languages, in which the use of classifiers is either mandatory or optional in numeral NPs. However, classifiers carry different functions in these languages. Distinct classifiers may be used for object and subkind readings, or the use of classifiers has the effect of blocking subkind readings. Or classifiers may license both object and kind readings. The idiosyncrasy of classifier functions shows that selectional restrictions between objects and kinds need to be encoded in the semantics of classifiers.10 Furthermore, subkind readings are highly affected by the animacy hierarchy of nouns in English, Korean, and Malay. The easiness of subkind readings for NPs of lower animacy is cross-linguistically prevalent. Hence, the animacy degrees of nouns should be reflected in the semantics of numerals or classifiers.

For the proper treatment of subkind readings, I argue that the interpretation domain proposed by Nomoto (2010) needs to be further elaborated. Nomoto assumes that the domain of objects is separate from that of kinds. Objects make a lattice structure by the join operation and the group formation function, and kinds make another lattice structure by the same operation and function. However, an interrelated relation between the two domains is not considered in his analysis.

To see why an interrelated relation is needed between the two domains, let us consider the denotations of the proper names in the following:11

Obviously, The Alchemist does not refer to a single object of copy because what is published by Harper Torch is not a single copy but all the copies titled The Alchemist. However, the singularity of the NP does not allow it to denote a sum of copies. Then, the next candidate is a group or kind of the book. A group is an abstract entity that consists of all its members and a kind is another abstract entity that encompasses all the instantiations of the kind. Given the two notions, it is not easy to decide which one is more appropriate to represent the meaning of the NP in (22a). The same argument is also true with The Genesis in (22b). The Genesis is the name of a specific car model. Then, it does not denote an object but some abstract entity that includes all the cars named ‘the Genesis.’

Before going into the details of the problem, it needs to be considered whether this is a question worth pursuing. This problem arises because a group and a kind share many properties. Both of them are abstract atoms and represent a number of objects which may be located in disconnected times and places. In other words, The Alchemist delivers more or less the same interpretation whether it denotes a group or a kind. Then, what matters is not a decision between the two entities but why this problem arises from the beginning.

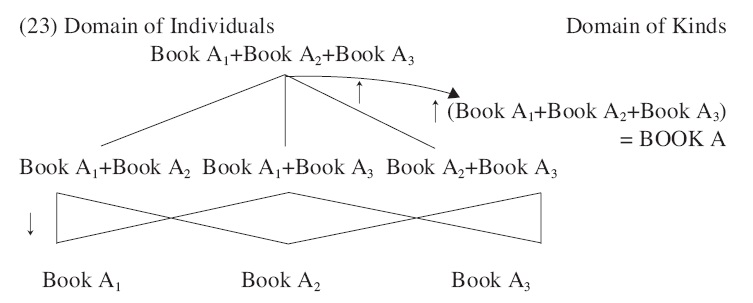
I argue that the unworthy selectional problem is attributed to the disconnectedness of the domains of objects and kinds. I propose that the grouping of objects by ↑ yields the group of the objects, which again corresponds to the kind of the objects. In other words, a group of objects makes a kind on the lowest level in the kind domain.

When all the copies of some book like Book A are grouped to a group like ↑(Book A₁+Book A₂+Book A₃), it is understood as a group of the copies. This group is also used as the title of the book, which is the kind BOOK A. The domains of objects and kinds are intertwined by the functions ↑ and ↓. Since a group of objects and a kind on the lowest level are not distinguished in this new domain, the selectional problem of the NPs in (22) is not an issue any more.

Kind and subkinds are relative concepts. Thus, once kinds on the lowest level are made by the grouping of objects, these kinds are grouped together to make another kind on the upper level. Suppose that copies of the book titled Book A make the kind BOOK A and that other book kinds such as BOOK B and BOOK C are made in the same fashion. In the situation that BOOK A, BOOK B, and BOOK C constitute an exhaustive set of books in the world w, BOOK A, BOOK B, and BOOK C are grouped to make the higher kind BOOK. A hierarchical structure of the kind domain is produced in the repeated grouping of kinds in this way.

In the lattice-theoretic domain of Link (1983), materials for mass terms make a separate lattice structure from that of objects for count terms. Although materials and objects are distinct in their atomicity, they constitute the same structure. In a lattice structure, materials are joined to make sums and also grouped to make groups. When groups are made by ↑, they serve to make a kind domain. Although materials are non-atomic and non-countable, kinds of materials are countable like kinds of objects. Hence, mass terms occur freely in count noun contexts, and the same subkind readings are available for mass terms. Hence, two milks denotes two kinds of milk in this domain.

Bare plurals in English are construed in two ways, namely indefinite object readings and kind readings. To deal with the ambiguity of bare plurals, two basic approaches are adopted in literature. One is to assign only kind readings to bare plurals and derive indefinite object readings from the kind denotations when necessary (cf. Carlson 1977, 1989; Chierchia 1998). The other is to accept the ambiguity of bare plurals and postulate both object and kind readings for them (cf. Wilkinson 1991, Diesing 1992, Gerstner & Krifka 1993, and Kratzer 1995).

Nomoto (2010) adopts the former approach, which is kinds-based. Bare plurals uniformly refer to kinds, which are defined by ^∩, the nominalization operation of properties. Occurring with kind-level predicates like be extinct, bare plurals like dinosaurs denote kind entities. When bare plurals combine with object-level predicates like be buried, they have a type-mismatch problem. Object-level predicates take a set of  objects while kinds are atoms. Hence, the predicativizer ^∪ applies to kinds and yields sets of objects. Nomoto further argues that when numerals occur with bare plurals in kind readings, another mismatch problem  arises. Thus, he proposes the application of ↓ and Ident to bare plurals to derive subkind readings.

In the latter approach, bare plurals are ambiguous between objects and kinds. Object-level predicates combine with object-denoting bare plurals and kind-level predicates with kind-denoting bare plurals. If we adopt this ambiguity approach, not only predicates but also numerals should be distinguished in their arguments. Unlike predicates, most numerals yield either object or kind readings. Hence, I argue that numerals should be ambiguous between object-level numerals and kind-level numerals.

Numerals other than the singular one denote plural-numbered entities. Object-denoting bare plurals refer to sets of atoms and sums. Thus, the plurality property of numerals does not pose a problem in object readings. However, kind-denoting bare plurals refer to atoms of kinds, which do not accord with the plurality of numerals. To resolve this mismatch problem, the incorporation of ↓ is required in the semantics of numerals. Then, the numeral two is interpreted in two ways as follows:

The object numeral two^o is defined as in most literature. Taking a set of objects, two^o yields a set of objects which have two members. The kind numeral two^K is defined to take a kind and yields a set of its subkinds the number of which is restricted to two. Following Nomoto (2010), I also assume that a group of subkinds is mapped to a kind. Thus, to get a subkind reading, the reverse procedure is required to a kind. The bare plural books combines with two in accord with its type.

When the object-denoting bare plural books^O is taken as the argument of two^O, it denotes a set of books whose number is two. Taking the kinddenoting bare plural books^K, two^K applies ↓ to derive the subkinds of the kind book and yields a set of book kinds which have two members.

The two possible approaches to the semantics of bare plurals naturally lead to the two analyses for numeral readings. To see which one is more appropriate to deal with subkind readings, we will compare them closely. According to Nomoto (2010), the interpretations of books and two books are like the following:

The bare plural books denotes the kind BOOK consistently. When an object reading is required, the up operation ^∪ applies to the kind to derive a set of objects from the atom of the kind. The object reading of two books results from the application of the numeral to the object denotation of books. The subkind reading of two books is more complicated. Before combining with the numeral, the bare plural books should be type-shifted by ↓ and Ident. ↓ has the effect of getting subkinds from the atom kind, and Ident is needed to make a set of sums with the sum of the subkinds. The semantics of the numeral is quite simple. It takes a set of sums and yields a set of sums whose number is as described by the numeral. However, the complex type-shifting of the bare plural is indispensible to make the numeral interpretation simple.

In contrast, the current proposal follows the ambiguity approach of bare plurals and postulates the ambiguities of numerals. Here are the interpretations of books and two books under the current proposal.

The kind books and the object books are assigned different entities BOOK^K, and BOOK^O, respectively. The object reading of two books is simply derived by the application of the object numeral two^O to BOOK^O. The subkind reading of two books results from the application of the kind numeral two^K to the subkinds of BOOK^K derived by ↓. The lexical meanings of bare plurals and numerals are more complex than those of Nomoto’s analysis. Instead, less additional operations are needed to derive subkind readings. All in all, the current analysis shows the same degree of theoretical complexity as Nomoto’s analysis. A major difference between the two analyses is which part of the semantics takes more burden for subkind readings. Hence, a true choice between the two analyses is made by comparing their theoretical plausibility and empirical usefulness to account for subkind interpretations.

In Nomoto’s analysis, the kind domain is not connected with the object domain. On the other hand, the current analysis assumes that the kind domain is intertwined with the object domain because kinds on the lowest level are equal to groups of objects. This revised domain provides a more efficient framework for the interpretations of proper names.

Proper names and kinds are discussed to share many semantic properties, so they are assumed to denote atoms. (cf. Krifka et al. 1995) Although proper names denote atomic entities of kinds like bare plurals, they are not used as nominal predicates. Then, the up operation does not apply to proper names according to Nomoto’s analysis. This means that since the object reading of Prius is not defined, the object reading of two Priuses as in (28) is not defined either. Even when type-shifting applies to Prius, it only returns a set of subkinds of the kind Prius but not objects. To get the object reading of two Priuses, an additional meaning shift is required to change the proper name to an ordinary count noun. Under the current analysis, the kind numeral two^K applies to the kind Prius, resulting in two^K (↓PRIUS^K). When there is an intermediate level of subkinds for the kind Prius, two Priuses denotes two species of Prius, which are members of the kind.12 However, when the context does not imply an intermediate level, the member specification function ↓ maps two Priuses to two objects of cars named Prius. Since the revised interpretation domain takes the interrelated domains of objects and kinds, which entities are selected by the function ↓ between objects and kinds is solely determined by the specificity of the context. Hence, subkind and object readings of proper names are uniformly derived without postulating additional operations in the current analysis.

Another problem to consider in comparing the two analyses is the different preferences of subkind readings depending on the properties of nouns. As noted in section 3.3., the empirical problem with Nomoto’s analysis is how to block the subkind readings of human NPs with numerals.

Two books and two milks are construed as two kinds of books or two kinds of milks. However, this subkind reading is not available for two students. The kind interpretation of two students is represented as in  (30a) under Nomoto’s analysis and as in (30b) under the current analysis.

When two applies to the type-shifted students, it returns a set of sums of subkinds of students under Nomoto’s analysis. Similarly, when the numeral two^K takes the kind student, it also returns a set of subkinds of students under the current analysis. This means that when two and students are combined, the two analyses give more or less the same result. Then, there should be an additional mechanism to block the application of two to the kind students.

There are basically two conceivable ways for the blocking effect. One is to revise the interpretation domain so that kinds of human nouns are not connected with subkinds. To achieve this purpose, a quite ad hoc stipulation will be needed. Conceptually, the kind student may be divided into smaller kinds such as elementary school and middle school students, and kind terms like middle school students may occur in generic sentences. To block the subkind reading of two students, there should be a stipulation such that although the kind student and its subkind middle school student constitute part of the kind domain, they are not connected by the functions ↑ and ↓. Since it is very hard to justify this stipulation, the revision of the domain is not a recommendable way to deal with the problem.

Another way to achieve the blocking effect is to attribute lexical properties to nouns or numerals to restrict the application. Since numerals are not assigned separate interpretations depending on their argument categories, this lexical approach is not made used of in Nomoto’s analysis. Object readings are open to all bare plurals, so numerals cannot have lexical properties targeting human arguments. Unlike Nomoto’s analysis, the current analysis posits the ambiguities of numerals so that only kind numerals may have a lexical restriction as to human nouns. Hence, I propose that although object numerals are not restricted in taking their argu-ments, kind numerals do not take human nouns as their arguments.13 Then, the semantics of kind numerals is revised as in (31a).

Taking an argument x which is not part of the kind human, the kind numeral two returns a set of sums of subkinds of x whose number is two. Since the kind book is not part of the kind human in the domain, two  books gives the expected subkind reading. However, the kind student lies under the kind human in the hierarchical domain, so it does not meet the definition of two. Hence, the subkind reading of two students is not defined.

As observed in section 4.2, classifiers in the classifier languages carry diverse functions intra-linguistically and cross-linguistically. The diversity of the functions provides a theoretical ground to lexical restrictions on classifiers as discussed by Krifka (1995) in section 3.1. It is not easy to assume that nouns have significantly different meanings between classifier and non-classifier languages. Then, it is natural to postulate that semantic roles of classifiers are partly transferred to numerals in nonclassifier languages.14 If we assume that the selection between objects or kinds is described in the semantics of classifiers, we can also assume that  numerals in non-classifier languages may be restricted in their argument entities between objects and kinds. The parallel restrictions on classifiers and numerals are further supported by the fact that human nouns are less  likely to have subkind readings in Korean and Malay as well as in English. In view of the fact that predicates in English are lexically restricted in their argument categories between objects and kinds, the lexical restriction on numerals is not quite unexpected.

8I follow the animacy hierarchy discussed by Corbett (2000). (i) Animacy Hierarchy speaker > addressee > 3rd person > kin > human > animate > inanimate Personal pronouns denoting a speaker, addresses, and 3rd persons take the highest position. Other human nouns including kinship terms take the next positions. Finally, animate nouns have higher animacy than inanimate nouns. Corbett argues that the singular-plural distinction in a given language must affect a top segment of the Animacy Hierarchy. Just as the degree of animacy affects the plurality of nouns, it also affects subkind readings.  9The semantic roles of classifiers in general are not discussed in this study. Some researchers argue for the counting function of classifiers and others for expressing semantic categories of nouns.  10Nomoto (2010) argues that classifiers uniformly block subkind readings cross-linguistically. However, widely used subkind readings of classifier NPs in Korean make explicit counterarguments against Nomoto. See Kwak (2012) for more details.  11The corelatedness between kinds and proper names is well discussed by Krifka et al. (1995).  12Whether the kind Prius is on the lowest level or not depends on contexts. In the context of (28), there are no subkinds under the kind Prius. However, in other contexts as in (i), the specificity of the kind domain is further refined, and the kind Prius may consist of its subkinds which are divided by years. (i) The magazine tested a 2002 Toyota Prius with over 200,000 miles on it, and compared the results to the nearly identical 2001 Prius with 2,000 miles tested by Consumer Reports 10 years before. (cf. http://en.wikipedia.org/wiki/Toyota_Prius) Since the specificity of the object domain is also determined by contexts for independent reasons, the different specificity of the kind domain is not at issue. Chierchia (1998) also notes that the structure of kinds is affected by contexts.  13I do not exclude a possibility that a taxonomic kind larger than human is taken as the lexical restriction of kind numerals. As noted in section 4.1, not only human but also animals that are cognitively prominent are less likely to be construed as subkinds. Human nouns do now show contextual variations in their preferences for object readings. However, other categories of nouns are subject to contexts in their preferences and also show different variations of preferences among speakers. Therefore, I restrict the lexical restriction of kind numerals to the kind human.  14Wilhelm (2008) also provides an argument in this aspect. An atom-accessing function OU in the sense of Krifka (1995) is expressed by classifiers in classifier languages while it is expressed by numerals in non-classifier languages. Thus, Wilhelm argues that English numbers have a ‘built-in’ classifier. Greenberg (1990) states that classifiers form constituents with numerals, not with nouns. This provides further support for argument of the built-in classifiers of English numerals.

Although generic readings are delivered through diverse forms of NPs in English, previous research on genericity is highly focused on the semantics of bare plurals. Additionally, characterizing generic sentences are widely discussed, but kind sentences do not draw as much attention. Hence, I have concentrated on subkind readings of NPs with numerals in this study.

As for kind interpretations, Krifka (1995) and Chierchia (1998) provide interesting analyses. However, they do not go into the details of subkind readings. Adopting the kinds-based approach of Chierchia, Nomoto (2010) argues that kinds are groups of subkinds and suggests a refined interpretation domain for kinds and subkinds in a lattice-theoretic structure.

I have pointed out that subkind readings are not available to all NPs with numerals. Human nouns are not allowed to have subkind readings even when they occur with predicates taking kind entities. The different preferences for subkind readings are not confined to English. The same preferences are observed in classifier languages like Korean and Malay.

In Nomoto’s analysis, numerals are not ambiguous whether they take objects or kinds as their arguments. Hence, the different preferences for subkind readings are not easy to be fit in his framework because object readings are open to all categories of nouns.

For the proper treatment of subkind interpretations, I have revised the interpretation domain suggested by Nomoto although I have accepted the group readings of kinds. The separate domains of objects and kinds are neither conceptually convincing nor empirically useful, especially in the semantics of proper names. In the revised domain, I have followed the ambiguity approach as to the semantics of bare plurals and proposed separate interpretations of kind-level numerals. Unlike object-level numerals, I have proposed that kind-level numerals are under a lexical restriction which states that arguments for numerals are not part of the kind human in the kind domain. By this restriction, nonhuman nouns freely occur with numerals to have subkind readings while human nouns do not.

This lexical restriction is not idiosyncratic to English. Classifiers in classifier languages carry diverse functions as to kind readings, which need to be lexically restricted. If we assume that part of the roles of classifiers are transferred to numerals in non-classifier languages, a similar lexical restriction is also naturally expected in non-classifier languages like English.