The purpose of this paper is to offer an amendment to David Chalmers’ construal of computation and its role in cognition. Although I largely agree with his structural analysis of implementation, I think that it suffers from a lack of attention to what is actually implemented and what notion of implementation is presupposed in arguments in cognitive science. Chalmers stipulates that all computations be specified as combinatorial-state automata, but this makes his account of computation too narrow and ill-suited for the explanatory purposes of behavioral sciences.

Computational processes occur in the physical world, and their properties are not limited to those discussed in computability theory. I argue that properties of implementation that go beyond abstract properties of computation, such as timing considerations, are crucially important in cognitive research, and that a good theory of implementation should encompass them. I also stress that implementation should not be confused with modeling: instead of focusing exclusively on the formal models of computation, we should account for physical realization and its properties.

Before I go any further, a terminological note is in order. A standard technical notion employed in computer science to describe a formal structure of computation is “model of computation,” and I shall use it throughout this paper in this meaning only. Standard models of computation, such as a Turing Machine or lambda calculus, are highly abstract and describe only how functions are computed. For example, the Turing Machine formalism does not say how much real time one step of computation takes (note, however, that it is possible to create a formalism that does exactly that: Nagy & Akl, 2011). It is important not to confuse this notion of model of computation with the one used in philosophy of science, e.g., to refer to computational models of the weather. Both are formal models that are supposed to represent reality (accordingly, computation or weather), but with different purposes and in different ways.

At the same time, because the question of how formal models represent reality has been the traditional focus of philosophy of science, I submit that accounting for physical computation, which after all is a special case of that more general problem, does not call for a completely new approach. Indeed, with so many valuable insights already on the market, ranging from theory of measurement to various accounts of explanation, the idea of analyzing the notions of computation and implementation by subsuming them under a more general conception seems only natural. In essence, this is what I propose to do in this paper: like many philosophers of cognitive science today, I espouse a general neo-mechanist conception of explanation, which, as I will show, is a natural extension of Chalmers’ causal-structural view of computation. The approach I advocate leads to a plausible theory of implementation which makes more sense of explanatory practices in computational cognitive science than the traditional functionalist view.

The remainder of this article is organized as follows. I begin by presenting the basic idea of causal accounts of implementation and the problems they are supposed to solve. I then sketch the model of computation preferred by Chalmers and argue that it is too limited to do full justice to computational theories in cognitive science. I also argue that it does not suffice to replace Chalmers’ favorite model with a better abstract model of computation; it is necessary to acknowledge the causal structure of physical computers that is not accommodated by the models used in computability theory. Subsequent to this, I outline a mechanistic proposal.

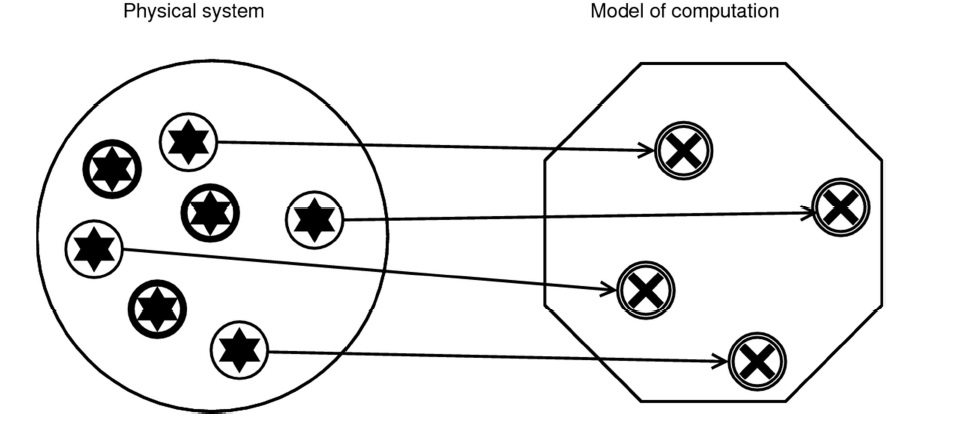
According to Chalmers’ causal-structural approach, implementation is a relation between the physical structure of a system and the formal structure of a computation. The theory says that “A physical system implements a given computation when the causal structure of the physical system mirrors the formal structure of the computation” (Chalmers, 2011, 328). One advantage of bringing causality into the picture is that it solves several problems that arise for traditional accounts of implementation appealing to an isomorphism between formal structure and a physical system.

The main difficulty with this traditional view is that it asserts a one-to-one correspondence between any state of the physical system and its formal structure. This seemingly innocuous claim has two related consequences, both of which are troublesome.

First, it implies that there have to be as few states in the physical system as in its corresponding formal structure. This conflicts with the intuitive view that some physical states must be inessential vis-a-vis the system’s computational characteristics: surely, the fact that, say, a sticker on my laptop computer is coming unstuck does not influence the performance of my word processor.

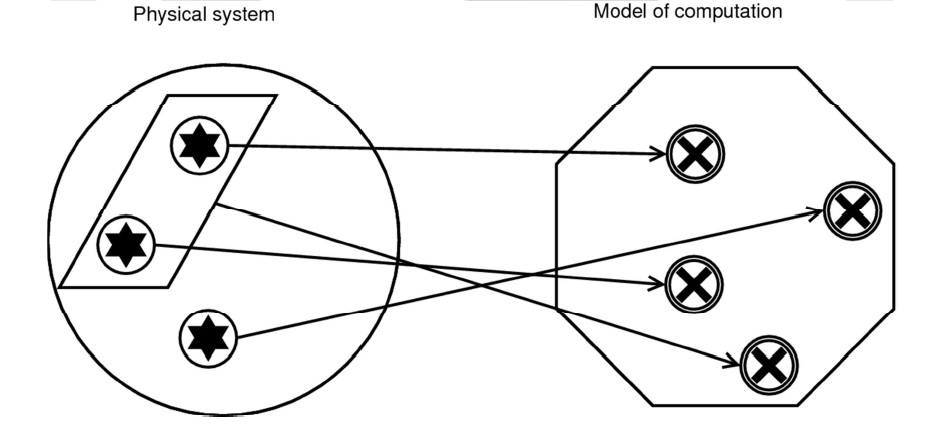
The second complication is even worse. Given that physical states are individuated within a particular theory and that different theories can carve the world at different joints, one can artificially generate any number of physical states in order to map them unto one’s favorite computation. So even if the physical system in question has fewer states than the mathematical construct, by using such set-theoretic operators as union (or their counterparts in a logical calculus), you can define as many physical states as required to interpret them in any way you want. This is how Putnam constructed his proof that any open physical system implements an inputless finite-state machine (Putnam, 1991). Such a description of the system will be complex but mathematically correct. Alas, this result makes the notion of computation more or less useless for the explanatory purposes of empirical science.

So what does one get with causality? The physical states taken to correspond to formal ones are simply causal factors, so one can eliminate causally irrelevant states (including those generated via Putnamesque redescriptions). The way to decompose the structure into its constituent parts is no longer just a matter of convention, which blocks the objection that the implementation relation holds between arbitrarily individuated objects in the world. Although one could still use the same mathematical tricks as Putnam did—since admittedly all causal ascriptions are theory-dependent—in practice the norms of causal explanation (and of explanation in general) require that it posit as few theoretical objects as possible. This means that parsimony considerations will take care of most such baroque ascriptions, including the ones necessary to turn a pail of water into a personal computer.1 Also, since on most accounts of word processor will come out false, it follows that a pail of water is not a kind of computer.

1To see how statistical measures of parsimony are used to choose among empirically equivalent theoretical models in psychology see e.g. Pitt et al. (2002).

So what is implemented? Without knowing this, we will not know whether the causal structure of the system actually corresponds to it. It seems obvious that it should be something that can be interpreted causally. This is precisely what Chalmers suggests when he claims that what is implemented are combinatorial state automata (CSAs).

Chalmers rejects the idea that what corresponds to a physical system are state transitions in a finite-state machine, with its inputs and outputs (if any). The justification is based on the fact that simple finite-state automata are unsatisfactory for many purposes, due to the monadic nature of their states. The states in most computational formalisms have a combinatorial structure: a cell pattern in a cellular automaton, a combination of tape-state and head-state in a Turing machine, variables and registers in a Pascal program, and so on. (Chalmers, 2011, p. 330)

He then goes on to defend the view that a theory of implementation ought to rely on CSAs instead. He cites four reasons for his choice of this model of computation. First, the “CSA description can … capture the causal organization of a system to a much finer grain” because it specifies states as vectors, not as monadic entities. Vectors can easily encode the states of various other kinds of machines. Second, CSAs are said to have more explanatory value than FSAs. Third, “CSAs reflect in a much more direct way the formal organization of such familiar computational objects as Turing machines, cellular automata, and the like.” The fourth reason is that CSAs may be generalized to accommodate finite and infinite machines (Chalmers, 2011, p. 331).

The problem with this justification is that it relies on the view that a physical structure is described by means of a formal system, which is then interpreted causally. Obviously, Chalmers’ interpretations are intended not to be arbitrary, but his assumption that there must be a single model of computation to which all others are equivalent introduces an element of arbitrary decision. Chalmers motivates his appeal to CSAs by saying: “To develop an account of the implementation-conditions for a Turing machine, say, we need only redescribe the Turing machine as a CSA. The overall state of a Turing machine can be seen as a giant vector ...” (Chalmers, 2011, p. 332). But, given the existence of other models of computation that satisfy the same requirements as CSAs, Chalmers’ choice is underdetermined at best.

The important point I want to make in this connection, and one that will reappear in section 5, is that although extensional equivalence of various models of computation is one of the most significant results of theoretical computer science, it tells us nothing about the causal complexity of the physical incarnations of these models. 2 Various models, if implemented physically, will differ in terms of basic causal structure. And in causal-structural accounts, we actually care for these structures, because they figure in causal explanations of behavior.

Turing machines were not invented to be implemented physically at all, but some people still build them for fun. Let us see if Chalmers’ claim will be plausible for such funny cases. Imagine a physical instantiation of a trivial logical negation Turing machine, built of, say, steel and rubber and printing symbols on paper tape. Its alphabet of symbols consists of “F” and “T”. If the machine finds “T” on its tape, it rewrites it to “F” and halts; if it finds “F”, it rewrites it to “T” and halts. Let us suppose that the machine’s head is so old and worn out that it tears the paper tape during the readout. As a result, no symbol will appear.

Now, the machine’s redescription in terms of a CSA cannot predict this: its vector contains no information about how a part of the system can be influenced by the wear of elements. Only when we describe the Turing machine literally, as a causal system that has a particular causal blueprint (engineering specifications of how it is built), can we causally predict such a breakdown.

Why are breakdowns and malfunctions so important? They help us discover the causal complexity of the system. It is well-known to what considerable extent the study of brain lesions and various deficits informs the formulation and evaluation of theoretical hypotheses in cognitive science (Glymour, 1994; Craver, 2007): without such evidence we would be completely unable to decide, on an empirical basis, which computations are actually implemented by the brain. At the same time, an abstract model of computation will not predict all the possible outcomes of the breakdown, as it abstracts away from a number of the system’s causal characteristics. So it will not tell us what is going to happen with the head; it will only say that the computation will no longer be correct.

There is a further problem with redescribing a machine in terms of CSAs. Let us suppose that my Linux laptop computer emulates an old Mac II series machine, using its old ROM. There is an ancient version of WordPerfect running on the emulated (virtual) Mac machine. Now, the crucial difference between the emulated Mac and my laptop is that the latter essentially emulates the Mac hardware and has its own causal dynamics as well. As before, a difference in causal dynamics is involved: in an old Mac, the emulator cannot break, because there is no emulator at all. To accurately describe what it is to execute a Mac program on my laptop computer one has to account for the emulator and my laptop rather than merely redescribe a Linux machine in terms of an old Mac. Given the importance of virtual machines in theories of mind (see e.g. Dennett 1991, Sloman 2008), we should allow for enough causal complexity to put the hypothesis of their existence in the brain to empirical test.

More importantly, measuring reaction time is one of the main empirical methods of testing hypotheses about mental processes in psychology and cognitive science (for a review, see Meyer et al., 1988). For example, the now classic results regarding the mental rotation of images relied on chronometric methods (Shepard & Cooper, 1982). Although some hypotheses about reaction time can rely on computational complexity considerations (Van Rooij, 2008), one still needs to know the causal complexity of the system in question to decide which of the extensionally equivalent models of computation is actually implemented. Note that the same point applies to the difficult question of whether serial or parallel processing is involved in a given cognitive capacity3 because the mathematical function computed by a serial automaton may be extensionally the same as that computed by a system employing parallel processing. Computational complexity of algorithms will not always be enough to decide empirically which is actually implemented; we also need to know the underlying machinery.

To sum up, cognitive scientists justify hypotheses about the implementation of cognitive processes by referring to non-formal properties and that includes spatiotemporal characteristics.4 This is what the talk of “details of implementation” is about. The task of philosophy of science, therefore, is to build a theory of implementation that acknowledges that. A related point is that many adversaries of the computational theory of mind point out that Turing machines are formal structures without any time-dimensions (e.g., Bickhard & Terveeen, 1995; Wheeler, 2005) only to argue against computational explanation, but this kind of objection is based on the same conflation of implementation with the formal model.

2Causal complexity is not to be confounded with computational complexity (Scheutz, 2001).  3For a discussion of how reaction time is related to this question in modern cognitive psychology see again Meyer et al. (1988).  4See the use of “implementation” in Marr (1982).

By relying on CSAs, Chalmers limits his account to digital effective computation—although some argue that inadvertently CSAs can compute uncomputable functions (Brown, 2004.) But any conception of implementation should be general enough to encompass various types of computation known in computer science, including unconventional ones, such as membrane computing or hypercomputation in a Malament-Hogarth spacetime (Hogarth, 1992). Philosophers are not privileged in their access to knowledge about computation; they know no better than computer scientists or mathematicians. Digital models of computation (which I call “classical” later on), extensionally equivalent to (or less powerful than) partial recursive functions, though prevalent in technological applications and presupposed in most variants of digital computationalism, should not be the only permissible kinds of models in a theory of implementation. True, usable forms of physical computation known today are probably not more powerful than a UTM,5 but the point of a theory of implementation should not be confused with that of the theory of computation, for computational equivalence does not imply implementational equivalence. We should be able, therefore, to distinguish between the implementation of a UTM that simulates, say, an analog computer and a physical implementation of the latter.

Chalmers argues that his theory of implementation accommodates analog computation because one can digitally simulate any analog system with arbitrary precision.6 Allen Newell defended a similar contention more explicitly by appeal to the sampling theorem (Newell, 1980, p. 177). But the claim that you can simulate any analog system digitally is true only in theory. In practice, however, no physical signal can satisfy exactly the conditions of the sampling theorem, and the reconstruction procedure (interpolation of the digital samples created from the analog source) cannot be carried out precisely. Now, one could still maintain that digital simulation is enough, since the analog source will also be noisy and cannot be measured with infinite precision (and both Chalmers and Newell argue this), but this does not serve the purposes of the theorist of implementation well.

An analog computational process will inevitably differ in terms of causal dynamics from its digital simulation. The upshot is that, having assumed at the outset that all computation is digital, Chalmers’ causal-structural approach cannot recognize any process as one instantiating an analog computation. This leads to the conclusion that there is nothing computational about analog processes and computation is just an artifact of simulation; a counter-intuitive view at best, especially if you also hold, like Chalmers, that simulating and realizing cognition are actually the same.

As a matter of fact, theories in computational neuroscience do posit analog and digital computation, distinguishing one from the other (O’Reilly, 2006). It is reasonable to suppose that such posits are not false a priori. Accordingly, philosophers would be well-advised to adopt transparent computationalism, as defended by Ron Chrisley (2001). Let us just accept whatever notion of computation will (or would) be used in ideal computer science.7 This is the first amendment I propose: extend the scope of admissible formal models to be realized.

5Arguably, analog networks operating on real values, like the ones described by Siegelmann (1994), are idealized distortions of neural networks that are subject to more noise than admitted by Siegelmann; this makes it less probable that they are really hypercomputational. However, if Siegelmann is right, my point is even stronger.  6Actually, Chalmers also mentions the possibility of representing state transitions by means of differential equations and describing states of the CSA as real, continuous values. It seems rather unlikely that this would work, as there is, to my knowledge, no general model of analog computation that is a universal model as well. Another difficulty is that the idea of using differential equations in this context, like the idea of constructing a digital simulation (on which I focus above), amounts to yet another redescription, and redescription is the real source of the problem.  7Piccinini & Scarantino (2010) recommend calling such computation “generic.”

If the point of the theory of implementation were to model any computation in cognitive science, Chalmers should abandon CSAs in favor of Abstract State Machines (ASMs), a formalism developed with precisely that purpose in mind. I will argue, however, that even replacing CSAs with a formalism designed to describe other models of computation will not save Chalmers’ theory of implementation.

Let me begin by sketching the idea of the formalism. ASMs are a powerful tool used to model not only classical computation (Gurevich, 1995), including parallel computation (Blass & Gurevitch, 2003), but, in its extended versions, analog machines (Bournez & Derschowitz, forthcoming) and quantum algorithms as well (Grädel & Nowack, 2003). It is also employed in high-level system analysis in computer science (Börger & Stärk, 2003). Although the ASM thesis—that you can use ASMs to model any algorithm—has not yet been proven for all unconventional omputational formalisms, let me assume for the sake of argument that it is in fact true.

The axioms defining the notion of algorithm in terms of ASMs are as follows:

I. An algorithm determines a sequence of computational states for each valid input.

II. The states of a computational sequence are structures.

III. State transitions in computational sequences are determinable by some fixed, finite description.

The states in axiom II are understood as structures that fully determine the subsequent computational sequence. By adding the fourth axiom one can derive a proof of Church’s thesis for ASMs (Dershowitz and Gurevich, 2008).

IV. Only undeniably computable operations are available in initial states.

Without axiom IV, oracles or genuine real numbers are admissible as initial states, rendering the computation non-classical.

One virtue of ASMs is that they can describe the behavioral dynamics of algorithms at several different levels of abstraction as well as model inter-component behavior on any desired level of detail. One can replace abstractly specified components of the system by an increasing number of concrete elements, thus gradually refining the description. One may, in effect, start with a general abstract specification of an algorithm and step by step add details until the final implementation is reached. Because the ASM formalism allows one to be general and specific according to one’s needs, it seems much more flexible than either CSAs or FSAs, not to mention Turing machines. No wonder, then, that ASMs are used to analyze various computer architectures, evaluate program correctness, assess whether code complies with specifications, etc.

To sum up, as state-transition systems, ASMs are easily interpretable in causal terms, which gives them an advantage over CSAs. The question then is whether it is really required that a philosophical theory of implementation use this tool rather than another. It is important to ask this question before we go on to define formally when a physical computational process is accurately represented using ASMs.

While Chalmers defends his choice of CSAs as the correct formalism to describe models of computation by saying that one can redescribe other models in terms of CSAs (which he takes to be a virtue), the redescribed models cannot mirror the causal dynamics of physical incarnations of other machines. This means that his account is no longer purely causal, which leaves a door open for arbitrary Putnamesque ascriptions. But since ASMs also represent all the other computational models in an abstract way, they will not match those of their properties that influence the processing speed at the hardware level. So we have less explanatory value than expected: we cannot use reaction time in full to distinguish physical implementations.

Indeed, any abstract model of computation, whether it be CSAs, ASMs, or UTMs, will be too limited, as its purpose is not to model the time-dimension exactly. We need to include something more in our account of implementation: the physical process cannot be just a mirroring of abstract models that were never designed to include all causal dimensions of computation.

There is a second problem with ASMs. What about some other, possibly not equivalent, models of computation that can be used to describe computational systems on the level of behavioral equivalence (i.e., including all inputs and intermediary states)? For the sake of the argument, I assumed this is impossible, but what if it turns out that some hypercomputational analog machines require essentially infinite descriptions (which violates axiom III)? In short, using any abstract model of computation, even as flexible as ASMs, could violate the thesis of transparent computationalism. For this reason, a philosophical account of implementation should remain neutral in the discussion over modeling computational systems on the level of behavioral equivalence.

To summarize, ASMs are a better modeling tool than CSAs. But physical implementation is not just a matter of modeling. Conflation of modeling with implementing seems to be at the core of the traditional isomorphism view on implementation: a physical system implements a computation just in case a description of the computation is true of the system, and it is true when the structure of the description is isomorphic to the physical structure of the system in question. Yet representations and models have different properties than their referents: a street plan is not the same as the city it represents. If you want to understand why I usually walk several hundred meters to the north of my apartment every other day, a standard map of Warsaw will not be helpful because it does not show kiosks where apples are sold. To understand my behavior, you need to know Warsaw (among other things) or to use a more fine-grained representation of it. Similarly, if you want to explain how people solve a certain class problems by positing mental rotation, a standard formal model of mental computation will not suffice because it cannot represent the speed of the computation. The reason is very simple: the purpose of the standard models of computation is to describe a system’s behavior as far as the steps of the computation are concerned. What is needed, then, is a rich causal model rather than an abstract mathematical specification. This is the second amendment I propose.

In the foregoing I have proposed two amendments to Chalmers’ theory: first, that it should cover all the kinds of computation; second, that it should include the causal structure as part of implementation. Neo-mechanism offers a natural framework in which to combine these amendments (Machamer, Darden & Craver, 2000; Craver, 2007).

Mechanistic conceptions of implementation, such as the one offered by Piccinini 2007, are a subclass of causal-structural accounts.8 In contradistinction to traditional functionalist views on computation, they require that all causally relevant details be given (Piccinini & Craver, 2011).

Piccinini (2007) focuses on digital computation, and has only recently admitted the need to accommodate non-standard models, all under the umbrella of “generic computation” (Piccinini & Scarantino, 2010). His general scheme of describing computational models is based on abstract string rewriting accounts of computation: computation is construed as rewriting strings of digits.

A computing mechanism is a mechanism whose function is to generate output strings from input strings and (possibly) internal states, in accordance with a general rule that applies to all relevant strings and depends on the input strings and (possibly) internal states for its application. (Piccinini 2007, 501)

his is suitable for digital computation but not for computing mechanisms that take genuine real numbers as input, and it is not obvious how to make it more general to cover generic computation. Moreover, string-rewriting systems are not so easy to map onto causal relationships as state-transition systems, for it is not at all clear what one should take as relata of the causal relations, if states are missing from the description. It is obviously not string values, but must rather be something that triggers the rewriting operation. Yet, in such a case, string-rewriting is mapped onto state transitions, and the original model is actually never used directly.

My suggestion is to remain both more general and less committed to classical computation. Computation is standardly understood as information-processing, so the notion of information can be used to define what is crucial about models of computation for the account of implementation. A computational process is one that transforms the stream of information it gets as input to produce some stream of information at the output. During the transformation, the process may also appeal to information that is part of the very same process (internal states of the computational process). Information may, although need not, be digital: that is, there is only a finite, denumerable set of states that the information vehicle takes and that the computational process is able to recognize as well as produce at its output. A bit of digital information construed this way is exactly equivalent to Piccinini’s notion of digit. (In the case of analog processing, the range of values recognized is restricted, but continuous, i.e., infinite.) By “information” I mean Shannon, quantitative information: the vehicle must be capable of taking at least two different states to be counted as information-bearing, otherwise it has no variability, so there cannot be any uncertainty as to the state it will assume. Note that the receiver’s uncertainty with regards to the state of the vehicle, which makes Shannon’s notion of information probabilistic in nature, has nothing to do with whether or not information-transmission is deterministic. Perfect, non-noisy channels still transmit information.

To say that a mechanistically adequate model of computation is implemented is to say that the input and output information streams are causally linked and that this link, along with the specific structure of information processing, is completely described. The description of a mechanistically adequate model of computation comprises two parts: (1) an abstract specification of computation, which should include all the causally relevant variables; (2) a complete blueprint of the mechanism on three levels of its organization. In mechanistic explanation, there are no mechanisms as such; there are only mechanisms of something: and here that something is (1). By providing the blueprint of the system, we explain its capacity, or competence, abstractly specified in (1).

Mechanisms are multilevel systems; they are composed of parts, which may be mechanisms themselves. The behavioral capacity of the whole system—in our case the capacity of the abstract model—is generated by the operations of its parts. According to Craver, every mechanism has three levels of organization: a constitutive level, which is the lowest level in the given analysis; an isolated level, at which the parts of the mechanism are specified, along with their interactions (activities or operations); and the contextual level, at which the function the mechanism performs is seen in a broader context. For example, the context for an embedded computer might be a story about how it controls a missile.

Now, only the isolated level corresponds to what was the traditional focus of philosophical theories of implementation; it is the only level at which the abstract specification of computation, namely (1), is to reflect causal organization. The causal organization of a mechanism will inevitably be more complex than any abstract specification. However, since we are building a constitutive explanation of a given capacity, only the causal variables relevant to that capacity will be included in our causal model. In normal conditions, the causal model of a mechanism, given as a set of structural equations or a directed acyclic graph (Pearl, 2000), will specify all the dynamics that reflect all the valid state-transitions of (1). However, it will also contain more, namely a specification of interventions that will render the computational mechanism malfunctional. So we can directly adopt Chalmers’ ideas about FSAs and CSAs to describe how the trajectory of state-transitions in the specification of computation reflects the proper subset of the causally relevant variables in the complete causal model, effectively

turning Chalmers’ definition into a scheme for various models of computation.

The isolated level is not autonomous, and the parts of the mechanism at this level should be localized, or identified, at the lower level independently of their computational roles—otherwise the whole description of the isolated level will remain unjustified. Notice that this principle of “bottoming-out” (Machamer, Darden & Craver, 2000) does not preclude the possibility of some parts being constituted in a distributed manner. It does, however, block Putnam-style tricks, since disjunctive states at the isolated level will have no counterparts at the lower level. The description of the lower level does not contain these disjunctions at all. Obviously, one could map a higher-level disjunction to a lower-level disjunction, but this does not satisfy the “bottoming-out” requirement. The principles of identity at the constitutive level come only from this level. You cannot explain how the higher-level objects are constituted at the lower level by saying that their constitution is determined at the higher level. This kind of top-down determination will fly in the face of the bottoming-out principle.9 Note also that this is not incompatible with using higher-level entities heuristically to discover lower-level entities.10

So instead of adding special provisos against using non-natural mappings, we simply require that the computational description at the isolated level not be completely independent of the constitutive level. In a similar vein, mechanistic explanation offers a way to individuate mechanisms (Craver, 2007; Miłkowski, forthcoming) that allows us to distinguish real systems from a mere hotchpotch of physical states. More importantly, parts of mechanisms are functional, and that helps to exclude from the set of mechanisms some physical systems, like tornadoes, piles of sand, or planetary systems (Piccinini, 2007, 2010; Miłkowski, forthcoming) that do not realize any capacity. In short, it can systematically answer difficult objections to Chalmers’ theory (Cocos, 2002) by saying what causal relationships are relevant, how to decompose systems, what parts of systems are, and so on.

Mechanistic explanation is deeply rooted in the methodology of cognitive science. For an early example, compare Allen Newell and Herbert Simon’s information processing system (IPS), which was essentially an abstract model whose architecture reflected certain psychological hypotheses about human problem solving, such as limited short-term memory (Newell & Simon, 1972, pp. 20-1). Besides sketching the abstract capacities of the IPS, Newell & Simon (1972, pp. 808-9) also described its relevant time properties. These properties were needed in order to use reaction time as empirical evidence.

Even if, by the lights of present-day mechanists, such models of cognition qualify as incomplete—they obviously fail to “bottom out” at the neurological level—Newell & Simon understood that in order to make the abstract structures explanatorily relevant they needed to relate them to their physical limitations. Similarly, contemporary computational modeling tries to integrate available neuroscientific evidence, and that is methodologically sound only if there is a causally-relevant difference between various physical implementations of computation. I take it as obvious that there is. And this was also presupposed in Marr’s methodology of explaining computational systems; his implementation level is not an isomorph of the algorithmic level (Marr, 1982).

What a computational mechanism is a mechanism of has traditionally been called “competence.” Newell & Simon (1972) accounted for competence by analyzing the cognitive task to be explained. Contrary to the received wisdom, mechanistic approaches explain cognitive competence with performance, and not performance with competence. This inversion means that data about performance are useful, and cognitive research is not just a matter of testing theoretical intuitions; it is also about experimental interventions and empirical data mining. Note that that is exactly what Newell & Simon did and claimed (1972, p. 11). They first performed task analysis to discover the nature of a cognitive capacity; then they described the behavioral performance of a single subject, and then they explained the performance with their computer model of the task. The immediate target of explanation was individual performance, but the distal target was also the competence, as the computer model was proven to be sufficient to solve the task. In Craver’s (2007) terminology, it is a how-possibly explanation.

To sum up, instead of requiring that one specify only an abstract model of computation, which is useful for computability theory, but not for computer engineering, one should require something that an engineer in a factory might use to actually produce a computer. There is no need to delve into purely abstract modeling via CSAs or ASMs at all. Some specification of abstract causal structure will be needed, of course, but this is not enough. In particular, what is implemented is not only the abstract model of computation but a complete causal structure of the mechanism, including its dynamics (i.e., state transitions).

8For a book-length account see Miłkowski (forthcoming).  9For a similar consideration see Piccinini (2010).  10For a story about how the psychological theory of memory helped to understand the hippocampus see Craver (2007).

In the foregoing I have proposed an alternative to Chalmers’ account of the implemented models of computation. While I endorse his causal-structural approach, my proposal is more mechanistic in spirit. The important point is that my (at least) three-level compositional account of mechanisms will engender hypotheses that can be tested using reaction times and various causal interventions. This means that it is more explanatorily and predictively relevant because it goes beyond formal modeling.

Chalmers stresses that modeling is explanatorily relevant as far as it maps the organizationally invariant properties of the physical system being modeled. This is why, by manipulating the model, we can predict and explain the behavior of the physical system. The same point was made long ago by Kenneth Craik (1943), who defined a model as “any physical or chemical system which has a similar relation-structure to that of the process it imitates” (Craik, 1943, p. 51). It is precisely this relation-structure that stays organizationally invariant and which is so important for computational modeling. In its mechanistic version, modeling can be brought to bear on more properties of the organization of physical systems than other structural or functional accounts allow. However, in order for that to happen, it is necessary to go beyond models of computation used in computability theory to use causal modeling in its full glory.