본 연구에서는 청소년의 진로와 직업결정에 중요한 영향을 미치는 수학자기효능감 척도를 개발하였다. 이를 위해 문헌연구와 설문조사를 토대로 기초 설문지를 구성한 후, 상담전공 전문가 5인의 평정을 거쳐 65문항의 질문지를 고등학생과 대학생에게 실시하여 40개의 예비 문항을 선정하였다. 예비문항을 고등학생과 대학생에게 실시하여 탐색적 요인분석을 실시한 결과 최종적으로 수학자기효능감 20문항이 선정되었다. 마지막으로 선정된 20문항의 5요인 모형이 적절한지를 확인하기 위하여 수학자기효능감, 수학 불안, 수학학습에 대한 자신감, 수학 신념,수학관련 진로선택 척도로 구성된 설문지를 실시하였다. 최종적으로 우리나라의 청소년들의 수학자기효능감 5개 요인-수학문제 효능감, 수학향상 효능감, 수학진로 효능감, 수학학습 효능감, 수학과목 효능감-이 확인되었다. 한편 수학자기효능감 척도의 구조와 문항들은 남학생과 여학생 집단에게 동일하게 기능하고 있었으나, 수학진로 효능감과 수학과목 효능감에서 남학생의 수학자기효능감이 여학생보다 유의미하게 높은 것으로 확인되었다. 개발된 수학자기 효능감 척도의 타당도를 확인한 결과, 수학자기효능감은 수학 불안, 수학학습에 대한 자신감, 수학 신념, 수학 관련 진로선택과 유의미한 상관이 있는 것으로 나타났다. 마지막으로 본 연구의 의의 및 제한점을 논의하였다.
역사적으로 볼 때 수학은 인류 최초의 학문이다. 고대 그리스 시대에서 학문이란 곧 수학을 말하는 것이었으며, 화음이론, 측량, 천체 관측 등 모든 것은 수학에서 비롯되었다고 볼 수 있다. 현대 사회에서도 수학은 과학은 물론 경제 분야와 일상생활 전반에 깊게 관여하고 있는 학문으로 경제활동에서 파생되는 경영 문제와 기업평가 등은 모두 수학을 통해 이루어진다. 이처럼 오늘날 수학은 과학과 사회의 발전에 큰 영향을 미치고 있으며, 그 중요성이 날로 증가하고 있다. 기본적인 일상생활을 영위하는 데에도 수학과 공학에 대한 이해가 필요하며, 특히 수학적 방법은 테크노로지 사회를 살아가기 위한 필수과목이라고 볼수 있다. 그러나 현대사회에서 수학의 중요성을 인식하는 사람은 소수에 불과하며, 대다수의 사람들이 적절한 수학적 능력을 갖추지 못하고 있다. 또한 많은 사람들이 수학이나 수학에 관련된 일에 관여하는 것을 회피하거나 불안하게 여기고 있다(허혜자, 1996).
그러나 우리나라와 같이 절대 자원이 부족한 국가가 IT 분야의 강국으로 성장한 원동력은 결국 대학이 우수한 엔지니어를 많이 배출함으로써 기술 산업의 발전과 연구계의 활성화가 이루어진 때문으로 생각할 수 있다. 그러나 현재 우리나라의 청소년들은 이공계를 기피하고 있는데 이에 대한 원인으로는 이공계 출신의 사회적 지위와 소득 수준의 하락, 이공계 진학 시 졸업 후 취업에 대한 문제, 이공계의 진로 전망이 불투명하다는 것과, 또한 어려운 것을 싫어하는 심리적 경향 및 수학과 과학 과목이 공부하기 힘들다거나 흥미가 없다는 등의 정의적 요인을 들 수 있다. 실제 인문계 고등학생들의 경우 국어, 영어, 사회과목의 성적이 낮을수록, 그리고 수학과 과학과목의 성적이 높을수록 자연계열을 선택하는 경향을 보였다. 또한, 전통적으로 여학생들이 수학과 과학 과목을 기피하는 경향이 강하므로 남학생보다 이공계열 선택을 더 꺼려하는 것으로 보고되고 있다(강혜정, 2003).
수학은 인류가 존재한 이래로 현재까지 인간의 산업과 기술 발달에 가장 지대한 공헌을 해 온 학문으로 볼 수 있다. 또한 현대사회는 예측할 수 없을 만큼 빠른 속도로 계속 변하고 있으며, 이런 빠른 기술 성장과 문명발달에 수학이 미치는 영향은 더욱 중요해질 것이다. 이를 반영하듯 새로운 수학의 분야가 계속 탄생하고 있으며, 수학에 사용되는 새로운 도구와 기법도 지속적으로 발전되고 있다(2006, 황종섭). 그러나 이처럼 수학의 중요성이 증가함에도 불구하고, 많은 사람들이 수학교과목을 기피하고 있으며 결국에는 개인의 진로 경로나 진로 선택권이 제한된다는 점을 고려할 때, 수학이 진로에 미치는 영향은 반드시 확인되어야 할 부분이다.
한국 교육과학기술부는 수학 교육의 필요성을 다음과 같이 설명하고 있다. 첫째, 수학적기초 지식은 사회생활에 필수적이며, 과학이나 다른 학문에 필요한 기초 학문이므로 수학은 국가발전에 도움이 된다. 둘째, 수학은 합리적이고 논리적인 사고력, 추상적 사고력, 창의적 사고력, 비판적 능력, 기호화하고 형식화하는 능력, 그리고 단순화하고 종합화하는 능력을 개발하므로 정신 능력을 신장시킨다(공귀옥, 2003). 사실 수학은 모든 나라에서 가장 기초적인 필수 과목으로 간주되며, 이는 수학이 실생활에 활용될 수 있으며 현대 문명과 기술의 발전에 도움이 되는 중요한 수단이기 때문이다(Dewey, 1997). 특히 현재와 같은 정보화 사회가 발전할 미래 사회에서는 거의 모든 직종에 종사하는 사람들에게 높은 수준의 수학적 문제해결 능력이 요구될 수도 있다. 사실 수학적 사고력은 수학에 대한 긍정적인 태도와 신념의 바탕 위에서 성장하고 발전될 수 있다. 개인이 수학에 관련된 성공경험과 체계적인 교과 경험을 통하여 수학 자신감과 같은 자기(Self)개념을 형성하게 되고, 이것이 궁극적으로 전공선택이나 진로선택으로 연결될 수 있기 때문이다. 이처럼 수학에 대한 인식이나 태도, 수행능력이나 수행행동 간에는 밀접한 상호관계가 있기 때문에, 개인의 수학에 대한 인식이나 태도에 대한 연구가 필요하다.
한편 수학에 대한 개인의 중요한 태도 변인으로 자기효능감을 생각할 수 있다. 자기효능감은 개인이 어떤 행동이나 활동을 성공적으로 수행 할 수 있는 자신의 능력에 대한 신념이기 때문에 성취행동을 예언할 수 있는 중요한 변인이 될 수 있다. 개인은 성취상황에서 여러 가지 방법을 통하여 자신의 효능수준에 관한 다양한 정보를 획득하며, 획득된 정보에 따라 효능감이 변화하고 결과적으로 행동변화가 일어나게 된다(이영희, 2002; Karsten & Roth, 1998). 결국 자기효능감은 대학의 전공선택과 학업수행과 같은 진로 진입행동에 대한 중요한 예언 변인이 될 수 있다(Lent & Hackett, 1987).
Bandura (1986)는 자기효능감을 개인이 어떤 행동이나 활동을 성공적으로 수행할 수 있는 자신의 능력에 대한 자신감으로 정의하였다. 이를 근거로 하여 Hackett와 Betz(1989)는 특정한 수학 과제나 문제를 성공적으로 수행할 것이라는 자신의 능력에 대한 상황적ㆍ구체적 문제의 판단으로 수학자기효능감을 정의하였다. 한편 국내에서 임은정(1998)은 특정 수학문제를 풀 가능성, 수학 관련과제를 수행할 가능성 또는 수학 관련 과정에 성공할 가능성에 대한 개인적인 판단으로 수학효능감을 정의하였다. 본 연구에서는 수학자기효능감을 수학과목이나 과제에 대해 개인이 지각하는 자신의 능력에 대한 효능감과 이후의 성공적 수행에 대한 신념(결과기대)으로 정의하였다.
Pajares(1996)는 자기효능감이 국어나 작문과 같은 학과목 보다 수학과 관련된 과제수행에서 더 상관이 높다고 보고하였다. Brown 등(1989)도 대학생을 대상으로 하여 수학자기효능감이 수학성적이나 수학결과 기대보다 수학에 대한 흥미와 수학과목 수강 선택에 더 중요한 예언변인임을 보고하였다(Brown, Lent, & Larkin, 1989). Hackett(1985)는 고등학교 과정의 수학에서(ACT 수학 점수) 수학자기효능감이 성별(gender)보다 더 중요한 예측요인이며, 대학의 수학 관련 전공 선택에서 수학자기효능감이 미치는 영향이 수학불안보다 크다고 보고하였다(Hackett & Betz, 1989). Hackett와 Betz (1989)도 대학생을 대상으로 수학자기효능감이 수학적 수행과 유의미한 상관이 있으며, 수학관련 전공의 선택과 유의미한 관련이 있음을 밝혔다. 이처럼 수학자기효능감은 개인의 여러 가지 수학 과목 선택 및 진로 결정에 영향을 미치는 중요한 요인이며, 궁극적으로 이공계열의 직업 선택과도 밀접하게 연결될 수 있다.
그러나 아직까지 우리나라에서는 수학의 태도와 인식에 대한 연구가 따로 구분되어 있지 않은 상황이며, 수학자기효능감에 대해서도 충분하게 다루어지지 않고 있다. 이러한 이유로 수학자기효능감은 수학자기(self)개념과의 구분없이 막연하게 같은 변인으로 인식되고 있다. 그러나 수학자기효능감은 자신의 수학능력에 대한 판단과 이후에 어떻게 행동할 것인가에 관한 예언적 개념으로 구분될 수 있고, 수학자기개념은 수학과 관련된 상황에서 자신에 대한 지각, 수학과 관련되어 형성된 긍정적, 또는 부정적인 자신의 현재 상태에 대한 개념 이라고 볼 수 있다(Gourgey, 1982). 따라서 자기개념은 전반적인 자기 이미지에 관한 것으로, 실제상황에서 개인의 수행정도를 예측하는 개념은 아니라고 볼 수 있다(Bandura, 1986).
자기효능감과 자기개념은 모두 수학적 수행 및 진로선택에 영향을 미치는 중요한 변인으로 밝혀지고 있다. 그러나 Pajares와 Miller(1994)는 수학문제해결에서 수학자기효능감이 수학자기개념보다 더 강한 예측력을 가진 변인이 라고 보고하였으며, Bong과 Clark(1999)도 자기효능감이 학업수행에 미치는 영향이 자기개념이 학업수행에 미치는 영향보다 더 일관적이라고 제안하였다(Bong & Clark, 1999). 자기효능감과 자기개념은 어느 정도 중첩되는 부분을 보이고 있지만, 과업과 관련된 효능감은 자기효능감에 가깝고 과제의 수행과 관련되어 형성된 자신에 대한 이미지 혹은 태도는 자기개념에 가까운 것으로 볼 수 있다. 따라서 자기효능감이 자기개념보다 학업적 수행 및 진로선택과 관련이 높은 것으로 볼 수 있는데, 자기효능감은 어떤 수행에 대한 개인의 확신감에 관련된 것이고 궁극적으로 행동변화를 통해 수행을 이끌어 낼 수 있기 때문이다. 이러한 근거로 볼 때, 개인의 수학과 관련된 진로의 선택에서 수학자기효능감이 수학자기개념보다 더 중요한 영향을 미칠 수 있음을 가정할 수 있다.
따라서 측정에서도 달라질 수 있는데, 수학자기개념은 개인의 수학에 대해 가지는 전반적인 이미지에 관한 질문(예: 당신은 수학을 좋아합니까?)을 사용하여 평가할 수 있는 반면에, 수학자기효능감은 보다 특별한 과제수행과 관련된 인지적인 질문(예: 당신은 이 문제를 풀 수 있습니까?)을 사용하여 평가할 수 있다(Pajares & Miller, 1994). 자기개념은 자신의 태도에 대한 인지적인 기술과 다른 사람과의 비교를 통한 평가인 정서적인 면으로 구성된 반면, 자기효능감은 자신의 과거 수행에 기초하여 미래의 행동을 예측하는 자신의 능력에 대한 인지적인 평가로 구성되어 있다(Bong & Clark, 1999). 따라서 자기효능감과 자기개념은 자주 같은 용어로 혼동되어 사용되지만 사실은 다소 다른 개념으로 보는 것이 바람직하다(Bandura, 1986).
그러나 수학자기효능감과 수학자기개념을 평가하는 연구들은 두 개념을 명확하게 구분하지 않고, 일반적인 수학에 대한 태도로 혼합하여 평가하고 있으며, 심지어 일반 자기효능감을 사용하여 수학 진로와의 연계를 찾기도 하고 있다(Norwich, 1987; Pajares & Miller, 1994). 하지만 수학자기효능감은 수학자기개념이나 일반 자기효능감과는 다른 변인이며, 따라서 수학 영역에 대한 자기효능감을 정확하게 측정할 수 있는 척도가 필요하다(Norwich, 1987; Pajares & Miller, 1994). 수학 영역에 대한자기효능감을 측정할 수 있는 도구가 없는 상황에서 이루어진 연구들은, 자기효능감의 중요한 부분인 전공선택 및 학습적 수행의 예언을 찾아내기 어렵고, 평가적이고 정서적(affective) 부분인 자기개념 요인과 혼동하여 측정하게 될 위험이 있다. 따라서 이러한 문제점은 개인의 수학 관련 전공 선택에 미치는 수학자기효능감의 영향을 명확하게 확인하려는 연구자들의 목표 달성을 어렵게 할 수 있다.
한편 Hackett과 Betz(1989)는 특정 수학 문제를 풀 가능성에 대한 개인적인 판단(수학문제 자기효능감), 수학관련 과제를 수행할 가능성에 대한 개인적인 판단(수학과제 자기효능감), 또는 수학관련 과정에 성공할 가능성에 대한개인적인 판단(수학관련 교과목 자기효능감)으로 수학자기효능감을 구분하였다. 또한 Multon등(1991)은 수학문제 해결력이나 수학과제의 성공적 수행에 대한 개인적 판단 능력인 수학 과제 해결력, 과제해결을 위한 노력, 그리고 과제해결에 대한 자신감을 수학자기효능감의 하위 요인으로 포함시키고 있다(Multon, Brown, & Lent, 1991). 이처럼 수학자기효능감은 다양한 하위요인들으로 구성되어 있을 가능성을 가지고 있다. 그러나 현재 우리나라에서는 수학자기효능감을 측정할 수 있는 도구가 개발되어 있지 않은 상황이며, 외국 척도를 번역하여 사용하거나 일반적인 자기효능감 척도를 사용하여 연구가 이루어지고 있다. 이러한 이유로 수학자기효능감의 중요성에도 불구하고 수학자기효능감에 관한 연구가 거의 이루어지지 못하고 있는 상황이다. 이에 본 연구에서는 개인의 전공 및 진로선택과 관련이 높은 수학자기효능감의 중요성을 제시하고, 이를 보다 정확하게 측정할 수 있는 수학자기효능감 척도의 개발을 목적으로 하였다. 그리고 개발된 수학자기효능감과 다양한 수학관련 변인들과의 관계를 확인고자 하였다.
본 연구는 청소년을 대상으로 하여 실시되었는데, 이는 대부분의 청소년들이 진로를 가장 중요한 고민으로 생각하고 있으며, 진로선택 및 직업결정이 청소년기의 중요한 발달과업이기 때문이다. 고등학교 시기가 되면서 개인은 자신의 진로를 선택하거나 장래의 생활방식을 선택하는데 있어서 체계적이며 현실적인 고려가 가능해지게 된다(최윤호, 2011). Super(1990)에 따르면 고등학교와 대학교 시기는 직업발달의 탐색기에 해당되는 단계로 개인은 잠정적인 진로를 선택하기 시작한다. 고등학교에서 시작한 진로탐색과 준비는 대학시기에서도 지속적으로 이루어지게 되며, 따라서 고등학교와 대학교 시기는 전공과 진로, 직업세계에 대해 탐색하며 자신의 장래를 결정하는 중요한 시기라고 볼 수 있다. 또한 대부분의 청소년은 고등학교 시기 이후 수학과목이 어려워진다고 지각하고 있기 때문에 이 시기에 개인의 지각하는 수학자기효능감은 진로와 직업의 선택과 결정에 중요한 영향을 미칠 수 있으며, 따라서 이를 확인하는 것이 필요하다.
한편 수학자기효능감에서 나타나는 성차에 대한 관심이 지속되어왔다. Hackett과 Betz(1981)는 효능감은 개인의 진로선택 결정에 중요한 영향을 미치며 특히 여성의 경우 낮은 자기효능감이 여자의 제한된 진로발달을 이해하는데 유용하다고 설명하였다. 전통적으로 여성적인 직업에서 여자들은 높은 자기효능감을 가지고 있으며, 비전통적인 직업에 대해 낮은 수준의 효능감을 가지고 있다. 많은 연구들에서 여학생들은 수학을 전통적으로 남자의 영역으로 지각하고 있으며, 따라서 남학생보다 낮은 수학자기효능감을 가지고 있음이 확인되었다(Brahier, 1995; Hackett & Betz, 1981; Post, Stewart, & Smith, 1991). 따라서 낮은 수학 자기효능감은 여성들의 진로선택과 방향을 제한할 수 있으며 수학자기효능감에 성차가 존재할 수 있다. 본 연구에서는 우리나라의 청소년들을 대상으로 하여 여학생들과 남학생들의 수학자기효능감을 비교하고 성차가 존재하는가를 확인하고자 하였다.
이러한 목적을 달성하기 위하여 본 연구에 서 설정한 연구문제는 다음과 같다. 첫째, 우리나라 청소년들이 지각하고 있는 수학자기효능감의 구성개념은 무엇인가? 둘째, 개발된 수학자기효능감 척도의 요인구조는 적합한가? 셋째, 수학자기효능감의 구성요인과 점수에성차가 존재하는가? 넷째, 개발된 수학자기효능감 척도의 타당도는 어떠한가?
먼저 청소년이 지각하는 수학자기효능감의 내용을 추출하기 위하여 대학생 227명(공과대학 112명, 심리학 전공수업 48명, 교양과목 67명)과 인문계 고등학교에 재학 중인 이과와 문과 고등학생 142명을 대상으로 설문조사를 실시하였다. 이를 성별로 구분하여 보면, 대학생은 남자 148명(65%), 여자 79명(35%)이었으며, 학년 별로 구분해 보면 1학년 57명(25.1%), 2학년 66명(29.1%), 3학년 52명(23%), 4학년 52명(23%)으로 구성되었다. 인문계 고등학생은 남자 68명(49%), 여자 74명(51%)이었으며, 학년별로 구분해 보면, 1학년 40명(28.2%), 2학년 34명(24%), 3학년 37명 (26.1%), 4학년 31명 (21.8%)으로 구성되었다.
두 번째 단계에서는 문헌연구, 설문조사를 통해 1차적으로 개발된 81개의 문항을 3명의 상담 전공 교수와 2명의 상담과정 박사가 평정한 후, 65개 문항의 설문지를 제작하여 서울 소재 대학생 271명과 인문계 고등학생 166명을 대상으로 예비검사를 실시하여 문항분석을 하였다. 이를 성별로 구분하여 보면, 대학생은 남자 174명(64.2%), 여자 92명(33.9%)이었으며, 학년 별로 구분해 보면 1학년 67명(30.8%), 2학년 73명(33.6%), 3학년 42명(19.4%), 4학년 35명(16.1%)으로 구성되었다. 인문계 고등학생은 남자 68명(40.9%), 여자 98명(59%)이 었으며, 학년 별로 구분해 보면 1학년 59명(35.5%), 2학년 48명(28.9%), 3학년 59명(35.5%)으로 구성되었다. 예비검사 결과 총 40개의 수학자기효능감 문항을 선정하였다.
다음으로 탐색적 요인분석을 위하여 서울소재의 인문계 고등학생 224명과 대학생 216명에게 40문항의 수학자기효능감 검사를 실시하였다. 표집 인원을 살펴보면 대학생은 단과대별로 공과대학 68명(31.5%), 상경대학 29명(13.4%), 인문대학 37명(17.1%), 사회과학대학 43명(19.9%), 자연대학 32명(14.8%), 기타 15명(6.9%)으로 구성되었으며, 성별로 구분해 보면, 남자 149명(69%), 여자 67명(31%)이었다. 학년별로 구분해 보면 1학년 46명(21.3%), 2학년 66명(30.6%), 3학년 34명(15.7%), 4학년 69명(31.9%)으로 구성되었다. 인문계 고등학생은 문과 93명(41.5%), 이과 131명(58.5%)으로 구성되었으며, 성별은 남자 110명(49.1%), 여자 114명(50.9%)이었으며, 학년 별로 구분해 보면 1학년 149명(66.5%), 3학년 75명(33.5%)으로 구성되었다.
세 번째 단계에서는 위의 단계를 걸쳐 선정된 20개 문항의 5요인 모형이 적절한지를 확인하기 위한 설문조사를 실시하였다. 개발된 20개 문항의 수학자기효능감 척도와 수학 불안, 수학학습에 대한 자신감, 수학 신념, 수학관련 진로선택 척도로 구성된 설문지를 서울 소재의 대학생 415명과 고등학생 414명에게 실시하였다. 표집인원을 살펴보면 대학생은 단과대별로 공과대학 171명(41.0%), 상경대학 29명(6.9%), 인문대학 14명(3.4%), 사회과학대학 143명(34.3%), 자연대학 32명(7.7%), 기타 28명(6.7%)으로 구성되었으며, 성별은 남자 280명 (70.4%), 여자 135명(32.5%)으로 구성되었다. 고등학생은 문과 183명(44.2%), 이과 231명(55.8%)으로 구성되었으며, 성별은 남자 313명(75.6%), 여자 101명(24.4%)이었다. 표집인원을 학년 별로 구분해 보면 대학생은 1학년 90명(22.6%), 2학년 147명(36.9%), 3학년 106명 (25.1%), 4학년 74명(15.3%)으로 구성되었으며, 고등학생은 1학년 100명(24.2%), 2학년 202명(48.8%), 3학년 112명(27.1%)으로 구성되었다.
수학불안
수학자기효능감의 준거타당도를 확인하기 위하여 수학불안척도를 사용하였다. 수학불안척도는 Betz(1978)의 MAS(Mathematics Anxiety Scale)를 정경아(2003)가 번안하고 일부 문항을 수정하여 완성한 수학불안 척도를 사용하였다. 척도는 총 10문항으로 구성되었으며, 5점 척도로 평가된다(문항 예: 수학은 나를 불안하고 초조하게 만든다). Betz의 MAS는 Fennema와 Sherman(1978)의 MAS(Mathematics Attitudes Scale)중 ‘불안척도(anxiety scale)’를 개정한 것으로 선행 연구들에서 강한 내적 일관성과 안정성을 가지고 있는 것으로 밝혀져 왔다(Hackett & Betz, 1989; Cooper & Robinson, 1991). MAS는 원래 대학생 집단을 대상으로 개발되었으나 Pajares와 Urdan(1996)의 구인 타당화 작업을 통해서 고등학생의 수학 불안을 측정하는데도 신뢰로움이 밝혀졌다. 점수가 높을수록 수학불안이 높은 것으로 해석되며 본 연구에서 수학불안 척도의 전체 문항에 대한 내적일관성 신뢰도 Cronbach
수학학습에 대한 자신감
수학자기효능감의 수렴타당도를 확인하기 위하여 수학학습에 대한 자신감척도를 사용하였다. 수학학습에 대한 자신감을 측정하기 위해서 Fennema-Sherman(1976)이 제작한 수학태도척도 MAS(Mathematics Attitude Scale)를 신임철(1987)이 번안 제작한 검사척도 중 일부를 사용하였다. 수학태도척도는 수학학습에 대한 자신감, 수학의 유용성에 대한 태도, 수학의 성역할 적합성(남성영역으로서의 수학), 학습자에 대한 어머니/아버지의 태도, 학습자에 대한 교사의 태도, 수학학습의 동기성, 수학학습결과에 대한 태도의 총 8개 하위요인으로 구성되어 있다. 본 연구에서는 수학학습에 대한 자신감 척도만을 사용하였으며 이것은 수학을 잘 학습하고 성취할 수 있는지에 대한 학습자의 자신감을 측정하기 위한 문항이다(문항 예: 수학문제의 종류에 따라 차이가 있긴 하지만 문제 푸는 것에 어려움을 느끼지 않는다). 각 문항은 5점 척도로 구성되어 있으며 점수가 높을수록 수학 학습에 대한 자신감이 높은 것으로 해석된다. 신임철(1987)의 연구에서 수학학습에 대한 자신감의 척도의 신뢰도는 .84로 나타났으며, 본 연구에서의 내적일관성 신뢰도 Cronbach
수학신념
수학자기효능감의 수렴타당도를 확인하기위하여 수학신념척도를 사용하였다. Carter과 Norwood(1997)의 수학에 대한 학생의 신념검사, Kloosterman과 Stage(1992)의 Indiana 수학 신념검사, Schoenfeld (1989)의 학생의 기하학에 대한 인식과 수학에 대한 신념검사, Fennema와 Sherman(1976)의 수학에 대한 태도검사, Sandman(1980)의 수학에 대한 태도검사 척도와 남상엽(1999)이 사용한 수학적 신념검사 문항을 토대로 김용성(2000)이 수정․보완한 수학 신념 척도를 사용하였다. 수학신념이란 개인이 수학과 수학적 과제에 접근할 때 가지는 신념을 말하며, 본 척도는 수학에 대한 신념, 수학학습에 대한 신념, 자아에 대한 신념의 3가지 하위 영역으로 구성이 되어 있다. 본 연구에서는 개인의 수학신념을 확인하기 위해 수학에 대한 신념척도만을 사용하였다(문항 예: 수학은 매우 가치 있고 필요한 과목이다). 각 문항은 5점 척도로 구성되어 있으며, 점수가 높을수록 수학에 대한 신념이 긍정적인 것으로 해석된다. 김용성(2000)의 연구에서 신뢰도는 .90으로 나타났으며, 본 연구에서의 내적 일관성 신뢰도 Cronbach
수학관련 진로 선택
수학자기효능감의 수렴타당도를 확인하기 위하여 수학관련 진로선택 척도를 사용하였다. 수학 관련 진로선택 척도는 양희진(2005)이 개발한 과학관련 진로선택 인식에 대한 설문지를 참고로 하여 수학관련 진로선택에 맞도록 박미란(2010)이 수정, 보완한 것의 일부를 사용하였다. 본 연구에서 사용한 척도는 수학직업 세계의 인식, 수학관련 직업의 경제적 측면 이해, 수학관련 직업의 교육적 측면 이해에 대한 문항으로 구성되어 있다(문항 예: 나는 수학 관련 직업에 대해 잘 알고 있다). 본 연구에서 사용한 척도의 학생용 설문지를 구성하기 위해 박미란(2010)이 수학교육 전공 전문가와 대학원생에게 의뢰한 결과 문항의 내용타당도 지수는 81.7%로 나타났다. 각 문항은 5점 척도로 구성되었으며 점수가 높을수록 수학관련 진로선택에 대한 인식과 이해가 높은 것을 의미한다. 박미란(2010)이 보고한 수학관련 진로선택의 신뢰도는 .81이였으며, 본 연구에서의 전체 문항에 대한 내적일관성 신뢰도 Cronbach
통계 처리는 SPSS 15.0과 AMOS 7.0을 사용하여 실시되었다. 첫째, 개발된 설문문항이 적절한지를 확인하기 위하여 상관분석 및 탐색적 요인분석을 실시하였다. 둘째, 최종적으로 선정된 문항과 요인의 적절성을 확인하기 위하여 확인적 요인분석을 실시하였다. 셋째, 수학자기효능감의 성차를 확인하기 위하여 측정모형 동일성 검증과 잠재평균분석을 실시하였다. 넷째, 개발된 수학자기효능감 척도의 타당도를 알아보기 위하여 기존의 수학관련 변인들과의 상관분석을 실시하였다.
기존의 수학자기효능감과 관련된 내용을 주제로 다룬 연구문헌들과 측정도구들을 선정하여 수학자기효능감과 관련된 내용 280개 항목을 추출하였다. 이 중 비슷한 내용을 포함한 항목들을 같은 항목으로 묶고, 청소년에게 적절하지 않거나 수학자기효능감과 관련된 것으로 보기에 타당하지 않은 문항들을 삭제한 결과 총 183개의 수학자기효능감 항목들이 남았다. 이후 대학생 227명(공과대학 112명, 심리학 전공수업 48명, 교양과목 67명)과 인문계 고등학교에 재학중인 이과와 문과 고등학생 142명을 대상으로 본 연구에서 정의한 수학자 기효능감의 정의를 설명한 후, 연구진이 개발한 20개의 예시 중 4개씩의 진술문이 제시된 설문지를 배분하여(예: 한두 번 수학시험 점수가 낮더라도 다음 시험에서는 잘 할 수 있다고 생각한다, 수학과 관련된 직업(진로)을 선택해도 잘 할 수 있을 것이다, 수학은 열심히 하면 성적을 올릴 수 있는 과목이다 등), 청소년들이 지각하는 수학자기효능감에 대한 생각을 자유 응답형식으로 가능한 많이 적도록 하였다. 다양한 응답내용들이 산출되었기 때문에 15명 이상이 응답한 내용을 중심으로 162개의 원 자료를 추출하였다. 고등학생과 대학 생의 응답내용을 비교해본 결과 비슷한 내용으로 구성되어 있음을 확인할 수 있었으며, 동일하거나 비슷한 내용을 포함하는 항목들을 통합하고 수학자기효능감과 관련이 적은 내용들을 삭제하여 141개의 문항을 추출하였다.
문헌 연구에서 추출한 183개의 항목들과 설문을 통해 추출한 141개의 항목들을 대상으로 하여, 1명의 상담심리 박사과정과 1명의 교육상담 박사과정, 3명의 상담심리 석사과정생이 동일하거나 비슷한 내용을 가진 항목들을 통합하고 본 연구의 수학자기효능감 정의에 적 절하지 않은 항목들을 제거하며 정리하였다. 그 결과 총 81개의 수학자기효능감 항목들이 남았다. 이 문항들을 대상으로 5명의 전문가(상담심리학 전공박사 및 교수 3명과 교육상담 전공교수 2명)가 각 문항들이 우리나라 청소년들이 지각하는 수학자기효능감을 얼마나 잘 나타내 주고 있는지를 ‘매우 그렇지 않다(1점)’에서 ‘매우 그렇다(5점)’까지의 5점 척도로 평정하였다. 이 과정을 통하여 평균이 3점이 되지 않는 문항을 삭제하는 방식으로 내용 타당도를 평가하였다. 또한 전문가들이 문항을 검토하여 표현이 적절하지 않거나 부적합한 문항들을 확인하여 수정하였다. 이러한 과정을 통해 총 65개의 수학자기효능감 문항이 구성되었다.
65개 문항의 수학자기효능감 척도를 서울소재 대학생 271명과 고등학생 166명을 대상으로 예비검사를 실시하여 문항분석을 실시하였다. 문항추출의 원칙은 이순묵(2000) 등이 제안한 방안을 따라 문항의 요인 부하량이 .40이상이면서, 다른 요인에 .30 이상 중복하여 적재되지 않고, 다른 요인간 요인 부하량이 .10 이상 차이나는 문항에 대해서만 추출하였다. 이러한 조건에 부합하지 않는 10개 문항을 삭제하고, 예비검사에서 하위요인에 묶인타 요인 8개 문항을 삭제하였으며, 다른 요인에 남은 문항의 신뢰도 분석에서 문항 제거시 신뢰도가 전체 및 요인 신뢰도보다 높아지는 7문항을 삭제하여 총 40개의 예비문항을 선정하였다.
두 번째 단계에서는 최종문항을 선정하기 위하여 40개 문항에 대한 탐색적 요인분석을 실시하였다. 이를 위해 2011년 9월부터 3주에 걸쳐 서울 소재의 인문계 고등학교 교사 및 대학교수와 강사들의 협조를 얻어 인문계 고등학생 224명과 대학생 216명에게 40문항의 수학자기효능감 검사를 실시하였다. 요인분석은 SPSS 15.0을 사용하여 탐색적 요인분석으로 요인을 추출하였고 추출한 검사에 대해 scree검사를 실시하였다. 회전방법은 각 요인 간에 상관이 있을 것으로 가정하였으므로 사각회전(Direct Oblimin)을 사용하였다. 자료의 적합성 을 확인하기 위하여 KMO test와 Batlett’s sphericity test를 실시한 결과, KMO 값은 .94, Batlett’s sphericity test 값은 6924.50(
마지막으로 최종 선정된 20개 문항에 대하여 5요인 모형이 적합한지를 확인하기 위한 설문조사를 실시하였다. 설문조사는 본 연구에서 개발된 수학자기효능감 척도 20문항과 수학 불안, 수학학습에 대한 자신감, 수학신념, 수학관련 진로선택 척도로 구성되었으며, 2012 년 3월부터 3주에 걸쳐 서울 소재의 대학생415명과 고등학생 414명에게 실시하였다.
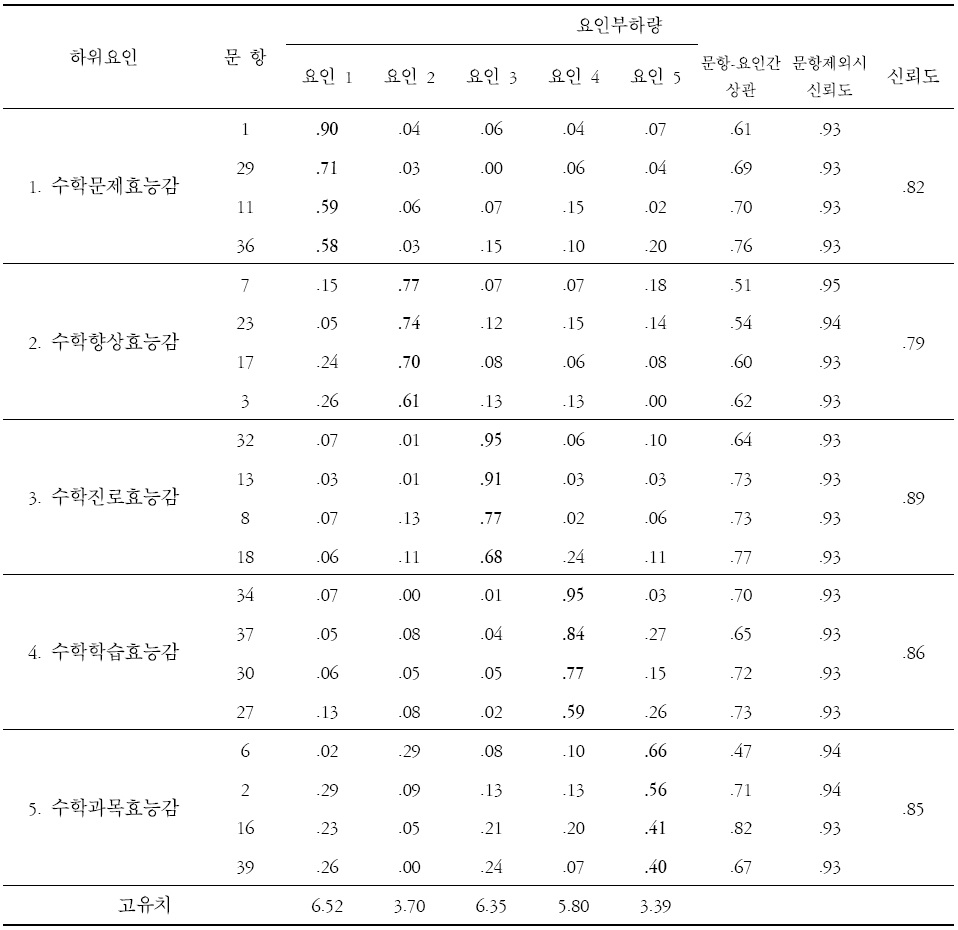
[표 1.] 수학자기효능감 최종문항의 요인별 부하량 및 문항제외시 신뢰도
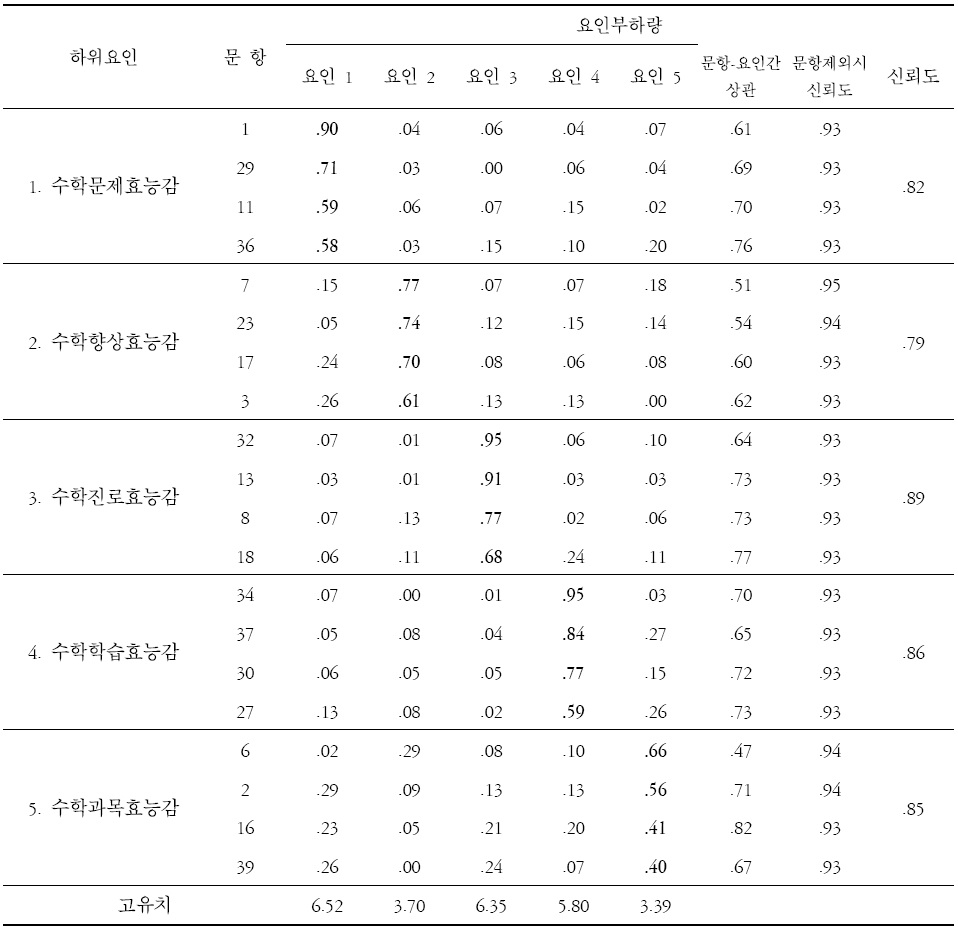
수학자기효능감 최종문항의 요인별 부하량 및 문항제외시 신뢰도
요인분석을 통한 Scree test 결과, 문항내용들의 해석 가능성과 문항의 내적일관성, 문항의 동질성 및 차별성을 기준으로 볼 때 5요인이 적절하다고 판단되었다. 이러한 절차를 통해 요인의 수를 5개로 가정하고 다시 요인분석을 실시하여 문항을 선별하였다. 그러나 요인분석에서 공통요인들에 의해 설명되어지는 변수의 분산비율인 공통성(communality)의 지수가 다소 낮은 문항들이 있어서(0.3 기준) 이를 제거하였다. 문항의 선별은 Pett 등(2003)이 제안한 기준을 토대로 자체 부하량이 .4 이하이거나 교차부하량(cross loading)이 .25를 초과하는 문항을 제거하여(Pett, Lackey, & Sullivan, 2003) 최종적으로 20개의 문항이 선정되었다. 최종적으로 선정된 20문항을 대상으로 SPSS 15.0을 사용하여 요인 수(N=5)를 지정하고 다시 사각회전(Direct Oblimin)을 실시한 결과, 5개의 요인은 각 4개 문항으로 구성되어 있었다. 최종 20문항들에 대한 요인행렬 및 문항별 부하량은 표 1에 제시하였다.
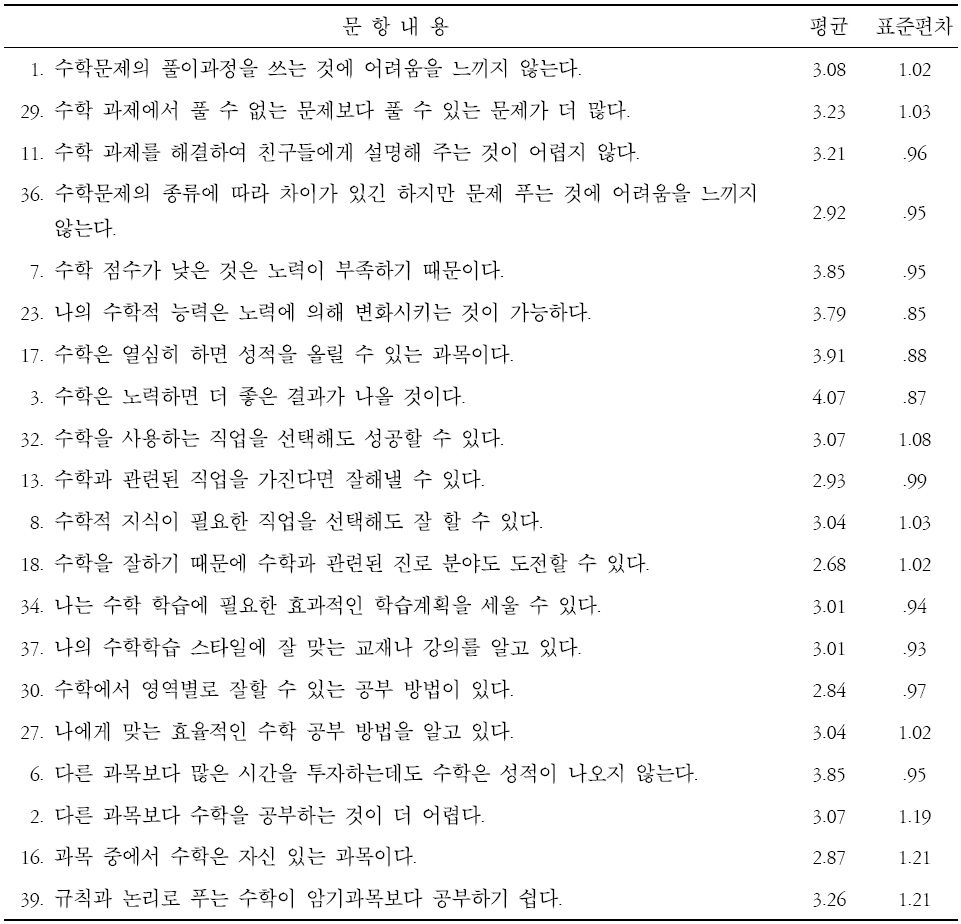
[표 2.] 수학자기효능감 최종 문항의 내용과 평균 및 표준편차
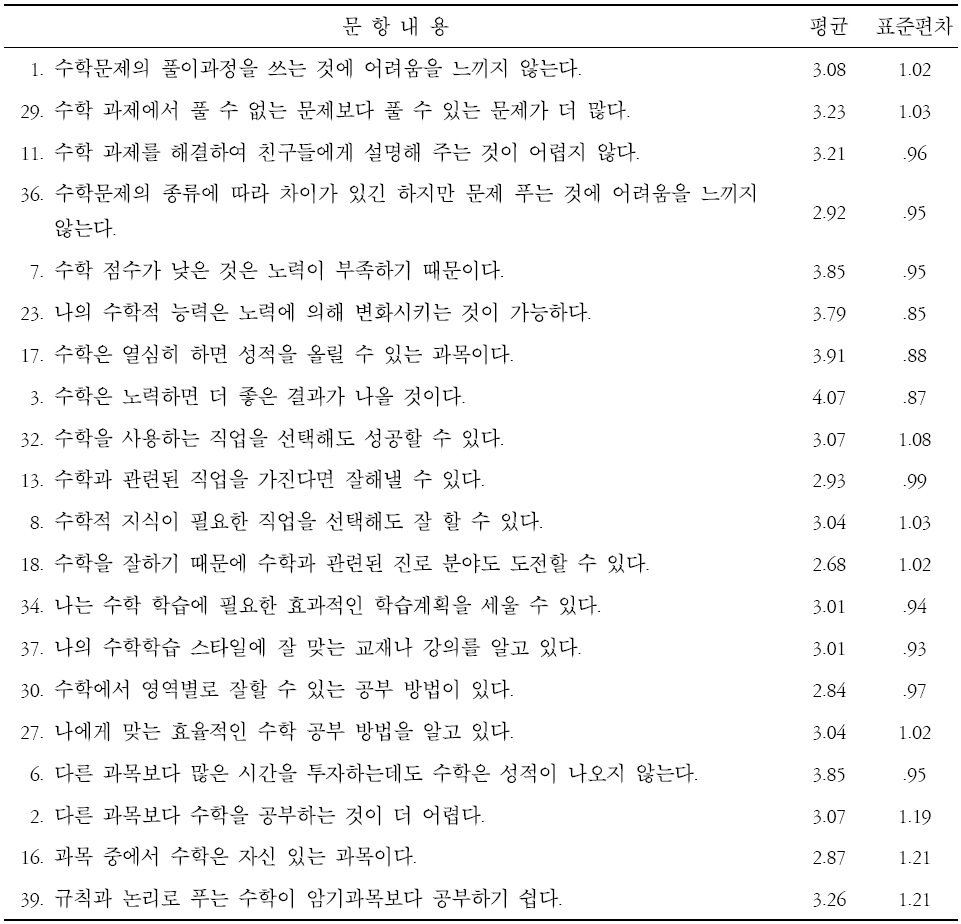
수학자기효능감 최종 문항의 내용과 평균 및 표준편차
요인 이름을 정함에 있어서 본 연구는 수학과 관련된 자기효능감에 관한 것이기 때문에 각 요인의 이름에 효능감이라는 말을 공통적으로 사용하였다. 수학자기효능감 요인 l은 수학 문제가 주어질 때 이를 잘 해결할 수 있다는 것과 관련된 효능감이므로 ‘수학문제 효능감’으로 명명되었고 요인 부하량이 .58∼.90였다. 요인 2는 개인이 스스로의 노력을 통해 수학에서 더 나은 결과를 얻을 수 있다는 효능감 내용이기 때문에 ‘수학향상 효능감’로 명명하였고, 요인 부하량은 .61∼.77이었다. 요인 3은 수학과 관련된 직업을 선택하여 성공할 수 있다는 것과 관련된 효능감이므로 ‘수학진로 효능감’으로 명명하였고 요인 부하량이 .68∼.95이었다. 요인 4는 수학을 공부하는데 있어서 효과적인 학습 방법을 가지고 있다는 효능감이기 때문에 ‘수학학습 효능감’으로 명명하였고 요인 부하량이 .59∼.95이었다. 요인 5는 다른 과목보다 수학 과목에 대해 개인이 가지고 있는 효능감에 관한 것이므로 ‘수학과목 효능감’로 명명하였고 요인 부하량이 .40∼.66이었다. 또한 각 문항이 신뢰도에 미치는 영향을 알아보기 위하여 각 문항 제거시 전체 신뢰도와 수학 자기효능감의 하위요인별 신뢰도를 표 1에 함께 제시하였다. 수학자기효능감의 최종문항과 문항별 평균은 표 2에 제시되었다. 개발된 수학자기효능감 척도의 전체 내적 일관성 신뢰도 Cronbach
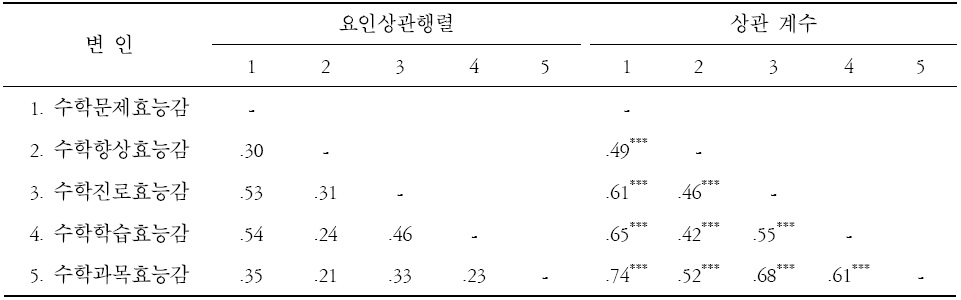
[표 3.] 수학자기효능감 척도의 요인상관행렬과 하위요인별 상관계수
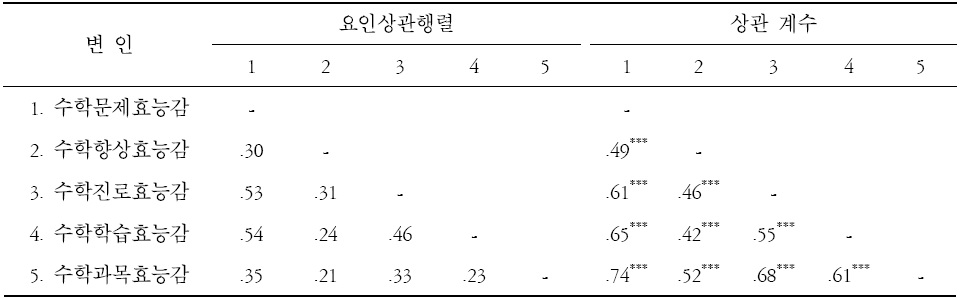
수학자기효능감 척도의 요인상관행렬과 하위요인별 상관계수
수학자기효능감 5개 요인의 성분 상관행렬과 하위요인별 상관계수를 구분하여 표 3에 제시하였다. 수학자기효능감 척도요인의 상관행렬은 .23에서 .54로 나타났다. 한편 수학자기 효능감의 하위요인 간의 상관계수는 .59에서 .74로 나타났으며, 수학자기효능감의 모든 하위요인들은 유의미한 정적 상관을 보이고 있었다.
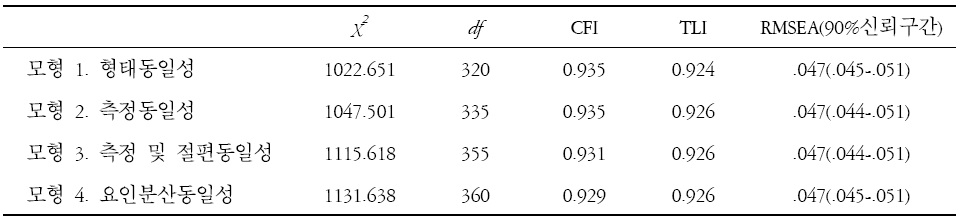
탐색적 요인분석을 통해 분석한 결과가 다른 집단에도 적용가능한지를 검토하기 위해 확인적 요인분석을 통해 교차타당화 작업을 수행하였다. 연구는 대학생 415명과 고등학생 414명을 대상으로 실시되었으며, 확인적 요인분석을 위해 구조방정식 모형분석을 실시하였다. 사용된 프로그램은 AMOS 7.0이었고 탐색적 요인분석에서 확인된 5요인 모형을 적합도 지수를 통해 확인하였다. 5요인 모형이 어느정도 적합한지를 알아보기 위하여
측정모형의 형태동일성 검증을 위해 수학자기효능감의 5요인 모형을 남학생과 여학생 집단으로 비교하였다. 수학자기효능감의 5요인 모형으로 형태동일성을 검증한 결과
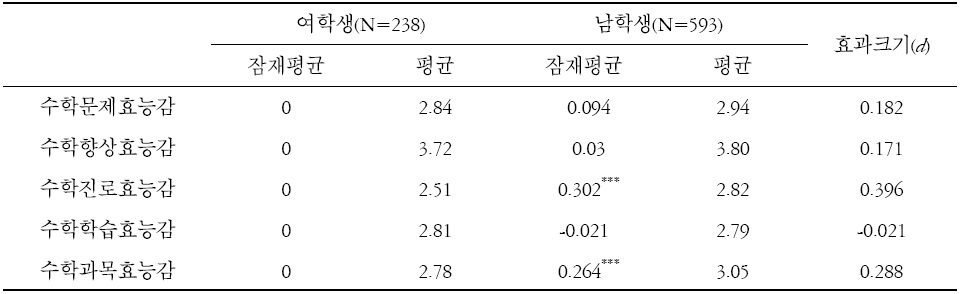
척도동일성이 확보되었기에 척도의 잠재평균이 남학생과 여학생에 따라 다른지에 대한 잠재평균분석을 실시하였다. 여학생 집단을 참조집단으로 각 잠재변수의 평균을 0으로 설정하여 여학생과 남학생 집단을 비교하였다. 산출된 잠재평균의 차이와 효과크기를 표 5에 제시하였다. 분석결과 여학생에 비해 남학생이 수학진로 효능감과 수학과목 효능감에서 잠재평균이 유의미하게 더 높은 것으로 나타났다. 잠재평균의 수준을 해석하기 위해 Cohen (1988)이 제시한 기준을 따르면 효과크기(
[표 4.] 남학생과 여학생 집단의 수학자기효능감 척도 동일성 검증에 대한 적합도 지수
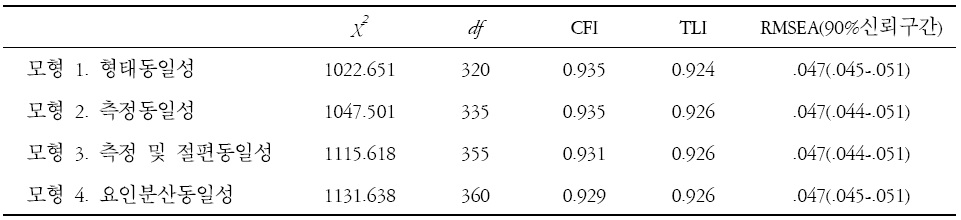
남학생과 여학생 집단의 수학자기효능감 척도 동일성 검증에 대한 적합도 지수
[표 5.] 남학생, 여학생 집단의 수학자기효능감 평균과 표준편차
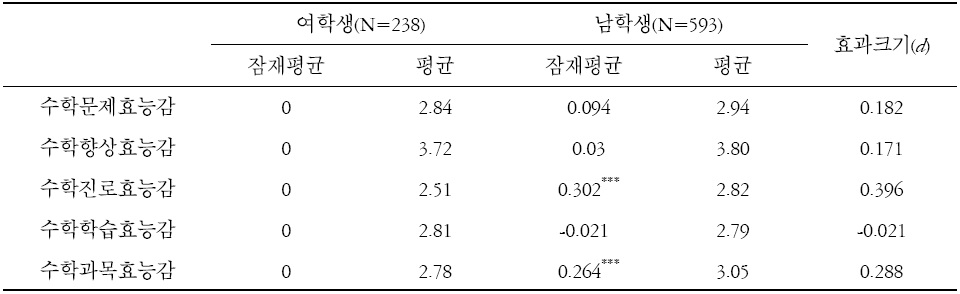
남학생, 여학생 집단의 수학자기효능감 평균과 표준편차
[표 6.] 수학자기효능감 척도와 관련 타당도 척도들 간의 상관관계

수학자기효능감 척도와 관련 타당도 척도들 간의 상관관계
>
수학 자기효능감 척도의 수렴타당도 및 준거타당도 분석
개발된 수학자기효능감 척도의 수렴타당도를 파악하기 위하여 수학학습에 대한 자신감, 수학신념, 수학관련 진로선택과의 상관을 분석하였다. 그 결과 수학자기효능감의 모든 하위요인들은 수학학습에 대한 자신감, 수학신념, 수학관련 진로선택과 유의미한 정적상관을 보이고 있었다. 또한 개발된 수학자기효능감 척도의 준거타당도를 검증하기 위하여 수학불안 척도와의 상관을 조사하였다. 그 결과 수학자기효능감 척도는 수학불안과 유의미한 부적 상관을 보였다. 결과는 표 6에 제시하였다.
최근 수학(mathematics)의 중요성을 강조하는 목소리가 높아지고 있는데, 왜냐하면 수학은 과학적이고 기술적인 직업의 선택 및 넓고 다양한 직업의 영역에 뛰어들기 위한 필수적인 학문이기 때문이다. 특히 우리나라처럼 인적자원의 중요성이 큰 나라에서는 수학(mathematics)과 관련이 높은 이공계열의 진로 및 전공 선택이 나라의 미래와도 관련될 것이라고 볼 수 있다. 그러나 이와 같은 수학의 중요성에도 불구하고 많은 사람들이 수학(mathematics) 교과목을 기피하고 있으며, 이는 결국 개인의 진로 경로와 진로 선택을 제한 시키는 악영향을 미치고 있다. 특히 수학(mathematics)이 진로에 미치는 중요성에도 불구하고 아직까지 국내에서는 수학과 관련된 연구나 척도의 개발이 부족한 상황이라고 볼 수 있다. 본 연구에서는 수학과 관련된 변인으로 자기효능감의 중요성을 제시하였는데, 수학 과목에서의 자기효능감은 특정한 수학과제나 문제를 성공적으로 수행할 것이라는 자신의 능력에 대한 상황적․구체적 문제의 판단으로 정의될 수 있으며(Bandura, 1986), 수학에 대한 흥미와 수학과목 수강 선택에서 중요한 예언 변인이 될 수 있기 때문이다(Brown, Lent, Larkin, 1989). 또한 수학자기효능감은 수학적 수행과도 유의미한 상관이 있으며, 수학 관련 전공의 선택을 예언하는 우수한 변인으로 밝혀지고 있다(Lent & Hackett, 1987).
그러나 수학자기효능감을 측정하기 위해서는 다양한 하위요인으로 구성된 측정도구가 필요하다고 볼 수 있는데(Hackett & Betz, 1989), 현재 우리나라에서는 수학자기효능감을 측정할 수 있는 도구가 개발되어 있지 않은 상황으로 외국의 척도를 번역하여 사용하고 있는 실정이다. 또한 수학 관련 진로선택에서 수학자기효능감의 중요성에도 불구하고 수학 자기효능감에 관한 연구가 거의 이루어지지 못하고 있는 상황이다. 이에 본 연구에서는 개인의 진로선택에 중요한 영향을 미칠 수 있는 수학자기효능감 척도를 개발하는 것에 목적을 두었으며 개발된 수학자기효능감이 수학관련 변인들에 미치는 영향을 확인하였다. 이상의 절차를 통해 얻은 결과를 바탕으로 본 연구의 결과를 요약하고 논의하면 다음과 같다.
첫째, 문헌연구와 설문조사 등을 통해 추출한 수학자기효능감의 내용들을 전문가 평정과 요인분석을 통한 타당화 과정을 거쳐 최종적으로 20문항으로 구성된 수학자기효능감 척도를 개발하였다. 기존의 진로연구에서 수학자기효능감의 중요성이 논의되어 왔으나 이를 측정할 수 있는 객관적인 척도가 부족하였음을 생각할 때, 본 연구에서 개발된 수학자기효능감 척도는 진로연구에서 개인이 지각하는 수학(mathematics) 영역에 대한 보다 세분화되고 명확한 자기 효능감의 측정을 가능하게 해줄 것이다. 지금까지 국내에서 이루어진 연구 들을 살펴보면, 외국의 척도를 번역하여 사용하거나 일반 진로자기효능감을 사용하여 측정한 것을 확인할 수 있다. 그러나 수학 영역에서의 효능감은 수학자기효능감을 사용하여 평가할 때 보다 정확하게 측정할 수 있을 것이다. 이에 대해 Bandura(1986)도 자기효능감이 과제특수적이기 때문에 평가해야 할 수행에 따라 다르게 측정해야 하며, 따라서 총체적으로 평가되기보다는 과제에 따라 다르게 평가되어야 함을 이야기하였다. 따라서 수학자기효능감은 일반 진로자기효능감이 아닌 수학영역에 관한 개인의 효능감으로 측정되어야 하며, 수학자기효능감 척도의 개발은 수학영역에 미치는 개인이 효능감 영향을 좀 더 명확하게 확인하기 위한 기본적인 과정으로 볼 수있을 것이다. 우리나라의 경우 많은 사람들이 수학 교과목을 기피하고 있으며 결국에는 개인의 진로경로가 바뀌거나 진로 선택권이 제한된다는 점을 고려할 때, 수학자기효능감 연구는 청소년의 진로를 이해하는 데 중요한 시사점을 제시해줄 것으로 기대할 수 있다. 더욱이 미래의 연구에서는 우리나라의 이공계 분야 발달과 활성화를 위해 수학자기효능감이 진로에 미치는 영향에 대한 세부적인 연구의 확장을 기대할 수 있을 것이다.
둘째, 수학자기효능감 척도의 요인분석을 실시해 본 결과, 각 4개의 문항으로 구성된 5개의 요인이 추출되었다. 수학자기효능감 척도의 5개 요인들을 살펴보면 다음과 같다. 요인 l은 수학 문제가 주어질 때 이를 잘 해결할 수 있다는 것과 관련된 효능감으로 수학문제 효능감, 요인 2는 개인이 스스로의 노력을 통해 수학에서 더 나은 결과를 얻을 수 있다는 효능감으로 수학향상 효능감, 요인 3은 수학과 관련된 직업을 선택하여 성공할 수 있다는 것과 관련된 효능감으로 수학진로 효능감, 요인 4는 수학을 공부하는데 있어서 효과적인 학습 방법을 가지고 있다는 효능감으로 수학학습 효능감 그리고 요인 5는 다른 과목보다 수학 과목에 대해 개인이 가지고 있는 효능감에 관한 것이므로 수학과목 효능감으로 명명되었다. 본 연구에서 나타난 수학자기효능감의 5개 요인들을 살펴보면 기존 외국 연구물 에서 밝혀진 수학효능감 요인들과 새로운 요인들로 함께 구성되어 있음을 확인할 수 있다. 수학문제 효능감, 수학과목 효능감 및 수학향상 효능감은 기존 외국의 척도에서도 확인되어진 요인들이며(Hackett & Betz, 1989; Multon, Brown, & Lent, 1991), 우리나라 청소년들의 수학자기효능감에서도 하위구성 요인으로 나타났다. 이외에 수학진로 효능감과 수학학습 효능감도 동일한 하위요인은 아니지만 기존 외국척도의 수학관련 과제효능감이나 수학과제해결에 대한 자신감 등의 요인과 비슷한 내용으로 구성되었음을 확인할 수 있다. 그러나 요인 이름을 정할 때 전문가들의 자문을 통하여 하위요인들의 문항과 내용을 고려한 결과, 좀 더 우리나라 청소년들에게 적합한 요인 이름으로 정해졌으며, 따라서 우리나라 청소년들이 지각하는 수학자기효능감의 세부적인 구성요인들을 좀 더 명확하게 밝힌 것으로 기대된다. 또한 본 연구에서 수학자기효능감을 수학과목이나 과제에 대해 개인이 지각하는 자신의 능력에 대한 효능감과 이후의 성공적 수행에 대한 신념(결과기대)으로 정의하였는데, 확인된 하위요인들이 정의에 잘 부합되고 있으며, 따라서 우리나라 청소년들이 지각하는 수학자기효능감의 내용을 잘 나타내주는 것으로 생각된다. 수학자기효능감의 각 요인에 대한 신뢰도 분석결과에서도 모든 하위요인의 신뢰도가 .79에서 .89사이의 신뢰도를 보이고 있어 본 연구에서 개발된 20개 문항들이 우리나라 청소년들이 가지고 있는 수학자기효능감의 내용들을 파악하는데 좋은 자료로 활용될 수 있음을 확인할 수 있었다. 또한 청소년의 진로지도시에 수학자기효능감의 전체점수 뿐만 아니라 각 문항별 또는 요인별 점수들을 구체적으로 살펴볼 수 있기 때문에, 수학관련 진로에 미치는 수학자기효능감의 영향에 대해보다 세분화된 진로지도 및 연구가 가능할 수 있을 것이다.
셋째, 청소년들이 지각하고 있는 수학자기효능감에 성차가 있는가를 확인한 결과, 수학자기효능감 척도의 문항들은 남학생과 여학생 집단에게 동일하게 기능하고 있음을 확인할 수 있었다. 그러나 수학자기효능감의 점수에서는 성차가 존재하는 것으로 확인되었다. 많은 연구들에서 여학생들은 수학을 전통적으로 남자의 영역으로 지각하고 있으며, 따라서 남학생보다 낮은 수학자기효능감을 가지고 있음이 밝혀져 왔는데(Brahier, 1995; Hackett & Betz, 1981, Post, Stewart, & Smith, 1991), 본 연구에서도 여학생들의 수학자기효능감 몇 하위요인들이 남학생보다 유의미하게 낮은 것으로 나타났다. 이를 좀 더 자세히 확인한 결과, 수학진로 효능감과 수학과목 효능감에서 여학생의 점수가 남학생보다 유의미하게 낮은 것으로 확인되었다. 이에 대한 내용을 살펴보면, 수학진로 효능감은 수학과 관련된 직업을 선택하여 성공할 수 있다는 것과 관련된 효능감이고, 수학과목 효능감은 다른 과목보다 수학과목에 대해 개인이 가지고 있는 효능감으로 설명될 수 있다. 따라서 우리나라 청소년의 경우, 여학생이 남학생보다 수학과목 자체와 수학관련 직업에서의 성공가능성에 대해 낮은 효능감을 가지고 있음을 알 수 있다. 그러나 한편 수학문제 효능감, 수학향상 효능감 및 수학학습 효능감에서는 유의미한 성차가 없는 것으로 나타나, 수학자기효능감의 하위요인에 따라 성차가 다르게 나타나는 것을 확인할 수 있었다. Randhawa 등(1993)은 남학생과 여학생의 수학자기효능감을 비교한 결과, 수학자기효능감의 모든 요인에서 남학생이 여학생 보다 높은 수학자기효능감을 가지고 있음을 보고하였다(Randhawa, Beamer, & Lundberg, 1993). 그러나 본 연구의 결과에서 볼 때, 우리나라 청소년의 경우에는 수학자기효능감의 하위요인에 따라 성차가 다르게 나타날 수 있기 때문에 미래의 연구에서는 수학자기효능감의 성차에 대해 보다 세분화된 연구가 진행되어야 할 것으로 볼 수 있다. 앞으로 수학자기효능감의 성차에 관한 결과는 지속적으로 확인되어야 할 과제이며, 또한 수학자기효능감의 하위요인으로 구분하여 남성과 여성의 진로선택에 미치는 영향의 차이를 확인하는 세분화된 연구가 필요할 것이다.
한편 남학생과 여학생 모두에서 가장 높게 지각하고 있는 수학자기효능감은 수학향상 효능감인 것으로 나타났다. 수학향상 효능감은 개인이 스스로의 노력을 통해 수학에서 더 나은 결과를 얻을 수 있다는 효능감을 내용으로 한다. 따라서 우리나라 청소년들은 자신이 노력을 하면 수학 점수가 올라갈 수 있을 것으로 긍정적인 지각을 하고 있으나 사실상 실제수학과 관련된 전반적인 효능감은 이보다 낮은 것으로 생각할 수 있다. 현재 수학의 중요성이 증가함에도 불구하고, 많은 사람들이 수학 교과목을 기피하고 있으며 결국에는 개인의 진로경로가 바뀌거나 진로 선택권이 제한된다는 점을 고려할 때, 수학자기효능감 중 수학향상 효능감이 높게 나온 것은 여러 가지 긍정적인 시사점을 제공하여 준다. 추후의 연구나 진로상담 프로그램에서는 청소년들의 수학향상 효능감을 기반으로 하여 수학자기효능 감의 다른 하위요인들을 높일 수 있는 방안을 모색해야 할 것이다. 또한 진로상담과 지도시에 수학자기효능감의 하위요인들을 고려하여 개인별로 낮은 수학자기효능감 요인에 대한 확인과 이를 위한 개선방안 등의 탐색이 세부적으로 제공되어야 할 것이다.
넷째, 청소년기에 개인이 가지는 수학효능감은 미래의 진로선택에 중요한 영향을 미칠 수 있다. 실제로 수학자기효능감은 수학성적이나 수학결과 기대보다 수학에 대한 흥미와 수학과목 수강 선택에 더 중요한 예언변인임이 보고되었고(Brown, Lent, & Larkin, 1989), Hackett와 Betz(1989)는 대학생을 대상으로 하여 수학관련 전공 선택에서 수학자기효능감이 미치는 영향이 수학불안보다 크다고 보고하였다. 본 연구에서는 개발된 수학자기효능감의 타당도를 검증하기 위하여 수학관련 변인들과의 상관분석을 실시하였다. 분석결과, 수학자기효능감은 수학관련 변인들과 유의미한 상관을 보이고 있었다. 수학자기효능감의 모든 하위요인들은 수학학습에 대한 자신감, 수학신념, 수학관련 진로선택과 유의미한 정적상관을 보였으며, 수학불안과는 유의미한 부적상관이 있는 것으로 나타났다. 또한 본 연구에 서 개발된 수학자기효능감 5요인 모형이 어느정도 적합한지를 알아보기 위해 확인적 요인분석을 실시한 결과, 개발된 수학자기효능감 척도의 5요인 모형 구조가 안정적인 것으로 확인되었다. 결과적으로 본 연구에서 개발된 수학자기효능감 척도는 모든 하위요인들이 수학관련 변인들과 유의미한 상관을 보이고 있는 것으로 나타났으며, 안정적인 모형구조를 가진 것으로 확인되었으므로 이후 수학(mathematics) 관련 진로 연구에서 유용하게 활용될 가능성이 크다고 볼 수 있다. 미래의 연구에서는 수학자기효능감의 하위요인에 따라 진로에 미치는 영향력의 차이를 세분하여 다양한 수학관련 변인들과의 관계 및 영향을 확인하는 작업이 필요할 것이다.
마지막으로 본 연구과정에서 나타난 제한점과 후속연구를 위한 제언을 살펴보면 다음과 같다. 첫째, 본 연구에서는 문헌조사 만이 아니라 실제적으로 우리나라 청소년들이 지각하는 수학자기효능감의 내용들을 반영하여 수학자기효능감의 문항들을 구성하려고 하였다. 이를 위해서 문헌연구와 설문조사 작업 등을 거쳐 수학자기효능감을 정의하였으며 이에 대한 설명과 예시문을 통하여 고등학생과 대학생들이 지각하는 수학자기효능감의 내용들을 조사하였다. 그러나 집단으로 설문조사가 이루어졌기 때문에 보완이 필요한 부족한 부분 이 있을 수 있다. 후속연구에서는 면대면 조사와 같은 심도깊은 질적 방법을 사용하여 본 척도의 문항에서 반영하지 못한 수학자기효능감의 구성요인이 있는가를 확인하여야 할 것이다. 둘째, 본 척도는 일부의 청소년을 대상으로 하여 만들어진 척도이며 수학관련 요인 중 수학자기효능감만을 연구의 주제로 다루었다. 따라서 수학관련 변인들과 수학자기효능감의 관계만을 살펴보았다. 그러나 개인의 수학관련 진로선택에서는 수학자기효능감 이외에도 수학자기개념, 수학신념, 수학태도 등의 다양한 변인들이 수학관련 진로선택에 영향을 미칠 수 있으며, 각 변인이 미치는 영향은 동일하지 않게 나타날 수 있을 것이다. 또한 본 연구에서 수학자기효능감과 수학학습 자신감과의 상관이 높게 나타나고 있는데, 미래의 연구에서는 이러한 개념들 간의 구분 및 확인작업이 진행되어야 할 것이다. 셋째, 본 연구 는 수도권에 재학중인 고등학생과 대학생만을 대상으로 하여 진행되었기 때문에 표집에 따른 효과가 나타났을 수 있다. 본 척도가 다른 연령의 집단이나 다른 지역의 고등학생과 대학생에게 실시하여도 동일한 연구결과가 나올지에 관한 지속적인 확인이 필요하다. 후속연 구에서는 연구의 대상과 연령을 다르게 구성하고 확대하여 본 연구에서 밝혀진 수학자기효능감 5요인 20개 문항의 적합성과 본 연구에서 나타난 결과가 동일하게 나타나는 가를 확인하여야 할 것이다.