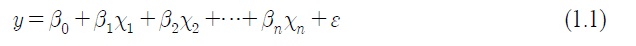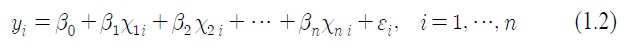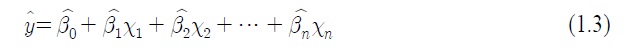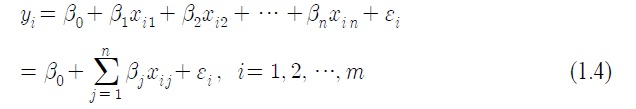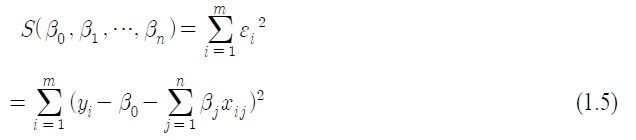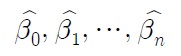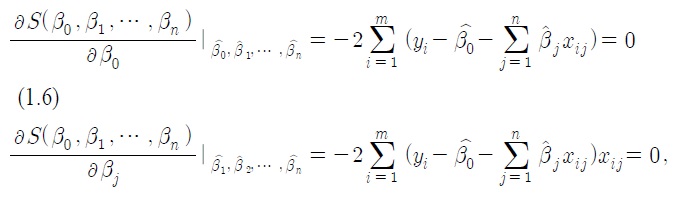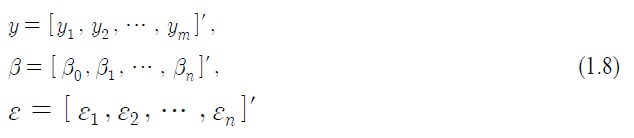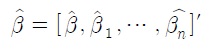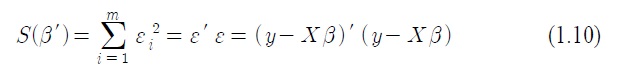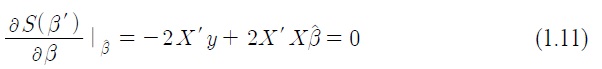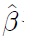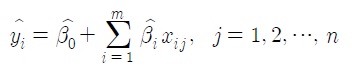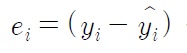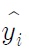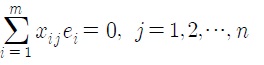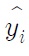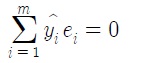ALC(Autoclaved lightweight concrete) 제조공정 중에서 예비양생이 완료된 반 경화제품(cake)인 상태에서 탈형을 실시할 때 적절한 탈형 시기가 지난 후에 탈형을 하게 되면 보습력이 떨어지고 절단 시 피아노선이 절단되어 제품에 균열이 발생할 우려가 있다. 이에 본 연구에서는 탈형 시기의 관리기준이 되는 경도(hardness)에 관한 예측을 하기 위해 관련된 변수들 간에 상호관련성을 찾고자 다중회귀분석 (multiple regression analysis)을 이용한 연구를 진행하였다. ALC 제조공정의 V/T(Vibration Time)대기, V/T동작, 발포 높이, 경화시간, 타설 온도, Rising, C/S비의 독립변수(Independent variables)들이 종속변수(Dependent variables)인 경도(hardness)에 어떠한 관련성이 있는지를 다중 회귀분석을 이용한 연구를 진행하였다.
현대 사회에서는 많은 문제들이 더욱 복잡하고 다양해져 관련된 변수(variables)들 간에 상호 관련성을 찾으려고 하는 경우가 많이 있다. 특히 공학문제나 경영·사회과학 문제 등을 다루면서 얻어진 자료에 대해서, 관련된 변수들 간의 관계를 설명(description)하거나 예측(prediction) 또는 추정(estimation)을 하는 것은 흔히 발생되면서도 중요한 문제 중의 하나이다. 이들 자료의 관계를 밝히는 기법의 개발은 여러 분야에서 활발히 이루어 졌으며, 그중 하나인 회귀분석(regression analysis)이 널리 사용되고 있다.
회귀분석을 할 때 가장 중요한 것은 무엇보다도 각 변수들 간의 관계를 충분히 반영하여 정확한 결과를 얻는데 있다(김광수, 1996).
최근 건축물의 고층화에 따른 건물자중에 대한 문제점이 발생하면서 구조물의 중량 부담을 경감하기 위해 비 구조용 재료인 경량콘크리트 제품의 사용이 급격하게 늘어나고 있는 추세이다. 경량콘크리트는 크게 경량골재콘크리트, 경량기포콘크리트, 무세골재콘크리트로 구분할 수 있다. 특히, 경량기포콘크리트(Autoclaved lightweight concrete, 이하 ALC)는 외국에서는 이미 범용화 되었으며, 국내에서는 주로 경량블록 등의 건식건축자재로 사용되고 있다(김영엽 외 3인, 2003).
ALC는 오토크레이브로 고온·고압하의 양생 과정을 거쳐 구조적으로 안정한 판상 구조의 토버모라이트(Tobermorite)결정을 이루는 과정에서 만들어지는 경량의 제품을 의미한다. ALC의 국제적인 학술용어는 AAC(Autoclaved aerated concrete)이며 이는 혼화제와 같은 화학물질로 콘크리트 내의 기포를 생성하여 자연 양생한 기포콘크리트와는 구별된다. ALC의 밀도는 0.5~0.7g/㎤의 경량으로 체적의 대부분을 기포로 구성하며 기포는 그 크기에 따라 거대기공과 미세기공으로 구분된다. 이들 기포는 전체 체적의 70~80%를 차지하며 구성물은 단지 20~30% 밖에 되지 않아 단열성, 내화성, 차음성 등이 우수하다.
지속적인 수요 증가와 우수한 장점을 지닌 제품을 생산하는 기업 또한 시장 환경 하에서 건강하게 생존하고 영속적인 경영활동과 경쟁력, 이익창출을 하기 위해 수많은 노력을 하고 있다(김영엽 외 3인, 2003).
ALC 제조공정은 원료의 분쇄 및 조합, 보강재의 준비, 혼합, 타설, 예비양생, 탈형 및 절단, 양생의 7단계로 분류된다. ALC 제조공정 중에서 예비양생이 완료된 반 경화제품(cake)인 상태에서 탈형을 실시하고 있다. 만일 적절한 탈형 시기가 지난 후에 탈형을 실시하면 보습력이 떨어지고 절단 시피아노선이 절단되어 제품에 균열이 발생할 우려가 있다. 절단 시 에는 반 경화제품의 적정온도, 양단부의 균열이 발생치 않도록 유의해야 하며 반 경화제품의 표면으로부터 표면 마감상태를 고려하여 표면절단을 실시한다(김덕재 외 13인, 1996). 이렇기 때문에 경도를 측정하여 탈형 시기를 관리하고 있다.
본 연구에서는 탈형 시기의 관리기준이 되는 경도에 관한 예측을 하기 위해 관련된 변수들 간에 상호관련성을 찾고자 다중회귀분석을 이용한 연구를 진행하였다. 경도에 대하여 다른 변수의 변화와 어떤 관련성이 있는지 관련이 있다면 어느 변수의 변화가 원인이 되고 어느 변수의 변화가 결과적인 현상인지를 분석하여 경도예측에 따른 ALC 제조공정에서 활용하고자 한다.
1.2.1 연구대상 및 측정방법
(1) 연구대상
ALC 제조공정 중 예비 양생된 반 경화제품(cake)의 경도(hardness).
(2) 측정방법
동일한 배합 비를 기준으로 타설 한 경량기포콘크리트 슬러리의 경화 진행과정을 독립변수별로 조건을 달리하여 독립변수별 변화에 따른 반제품의 경도를 측면 부 바닥으로부터 25㎝ 위쪽을 설비용량 0 ~ 20kgf이 측정 가능 한 경도측정기기(push pull gauge)로 경도를 측정한다(이레테크, 2005).
1.2.2 사용 재료 및 변수 데이터의 조건
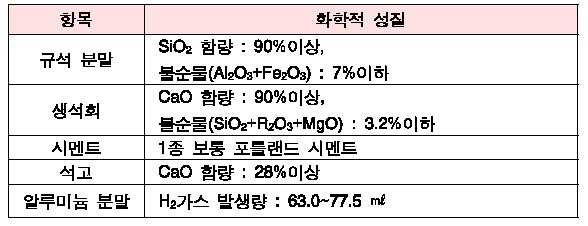
(1) 사용 재료의 화학적 성질은 <표 1>과 같다.
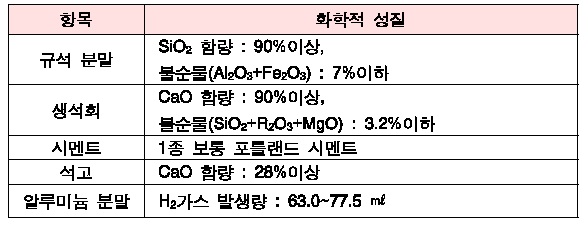
ALC 원.부자재의 화학적 성질
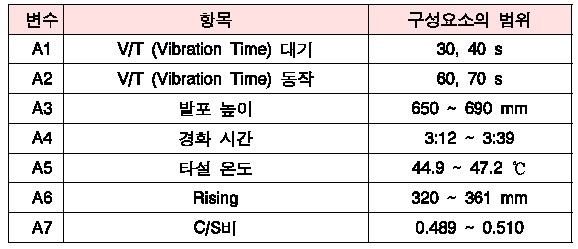
(2) 변수 데이터의 조건은 <표 2>와 같다.
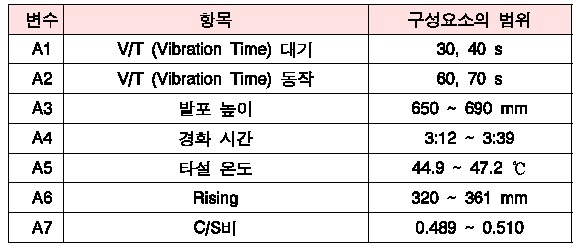
변수 데이터의 조건
1.2.3 독립변수와 종속변수의 데이터
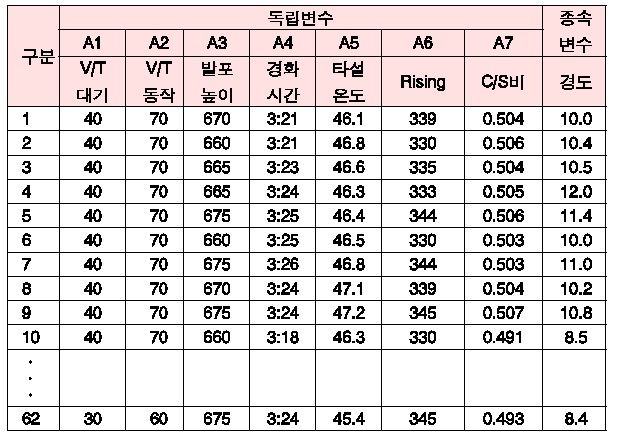
독립변수와 종속변수의 데이터는 <표 3>과 같다.
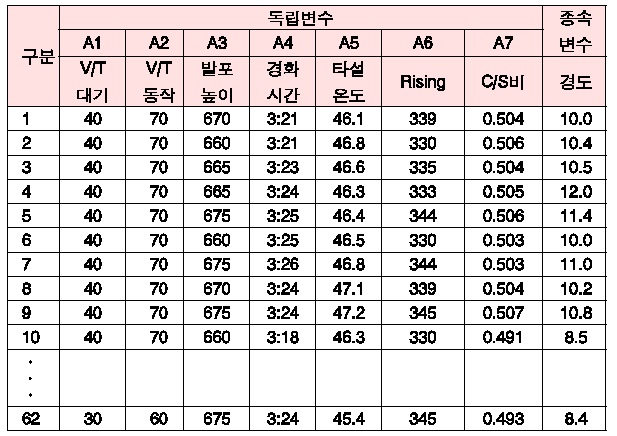
독립변수와 종속변수의 데이터
1.2.4 분석방법
Minitab 16버전 한글판으로 수집된 독립변수와 종속변수를 다중회귀분석을 이용하여 특정 변수의 변화와 다른 변수의 변화가 가지는 수학적 선형의 함수식을 파악함으로써 상호관계를 추론하는 회귀식을 산출하였다.
두 개 이상의 변수가 포함된 회귀모형을 다중회귀 모형이라 하며, 이때 자료들이 선형적인 관계에 있으면 다중선형 회귀모형(multiple linear regression model)이라고 한다.
다중 선형회귀모형에서
같은 방법으로
분석을 위하여 가지고 있는 데이터 (
에서 필요로 하는 가정은 다음과 같다(유성모 외 1인, 2006).
① 독립변수
② 오차 항
③ 오차 항은 정규분포를 따른다.
이때,
모수 추정에는 최소자승법이 사용되며, 만약
이때 오차의 자승 합은
식 (1.5)를 최소화하는
으로 두면 이들은 다음 식을 만족한다(김광수, 1996, 박성현, 2005).
식(1.6)을 최소자승 정규 방정식(least squares normal equations)이라 한다(김광수, 1996,박성현, 2005)).
이 연립방정식에서 추정치를 구하여 앞서 말했던 식(1.3)와 같은 예측 식을 만들 수 있다. 이것을 보다 간단하게 행렬로 표시하면,
와 같이 행렬로 표시되고, 이때
그리고
이다. 여기에서 최소자승 추정량(least square estimator)
을 구하기 위해서는
식(1.10)을 최소화하는 것으로 다음 식을 만족한다.
식(1.11)을 만족해야 한다.
이때
는 다음과 같다.
회귀모형의 타당성을 검토하기 위해 잔차분석(residual analysis)을 한다.
즉, 특정한 잔차가 타 잔차에 비하여 상대적으로 크다는 것은 회귀분석에 있어서 그 해당하는 자료가 모형에 적합하지 않다는 것을 나타내고 있다.
중 회귀모형을 데이터에 적합 시켜 얻은 추정식의 값
과
를 잔차(residual)라고 하며, 잔차를 검토함으로써 유용한 정보를 얻을 수 있다. 잔차들의 성질에 대하여 논하면 다음과 같다.
중 회귀모형 y =
즉,
(4) 잔차들의
에 의한 가중 합은 0이다.
즉,
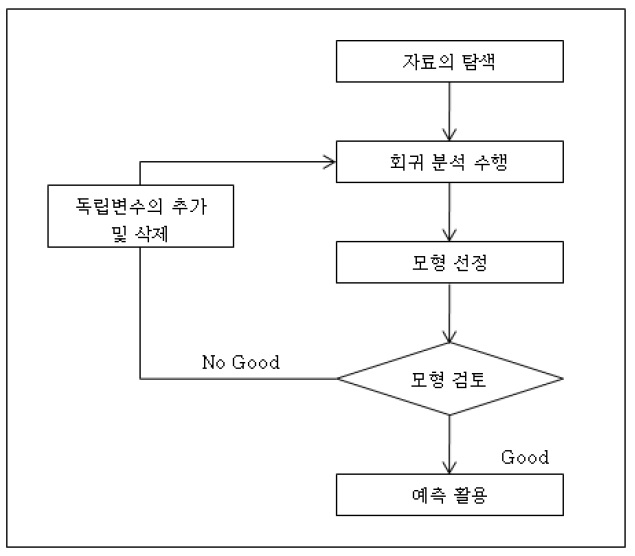
다중회귀분석의 절차는 다음 <그림 1>과 같다(유성모 외 1인, 2006).
다중 회귀분석에서는 여러 개의 독립변수들이 서로 상관관계가 없어야한다는 가정이 있다. 그 때문에 산점도, 상관분석을 통하여 변수들이 어떠한 관계를 가지고 있는가를 파악하는 것이 매우 중요하다.
종속변수와 독립변수를 구분하고, 독립변수의 수나 종속변수의 형태에 적절한 분석방법을 선택하여 분석한다. 독립변수가 여러 개인 다중회귀모형에서는 여러 복잡한 모형이 만들어진다.
(1) 회귀 분석
일반적인 최소 제곱법에 의한 단순 회귀분석 또는 다중 회귀분석을 수행하는 경우에 이용된다.
(2) 단계적 회귀 분석
회귀모형에서 독립변수를 선택하거나 제거하여 최적의 모형을 식별하기 위한 경우에 이용된다.
(3) 최량 부분 집합
지정한 독립변수 중 종속변수를 가장 잘 설명하는 독립변수를 구성하기 위한 경우에 이용된다.
(4) 적합선 그림
독립변수와 종속변수가 직선관계가 아니라 곡선인 경우에 이용된다.
(5) 부분 최소 제곱
독립변수들 간에 상관관계가 존재하거나 독립변수의 수가 관측된 데이터의 수보다 많은 경우에 유용하다.
(6) 로지스틱 회귀분석
종속변수가 범주형인 경우 이용된다.
회귀함수의 적합성, 회귀계수에 대한 유의성 검정 및 추정, 반응변수의 변화와 밀접한 관련이 있는 독립변수를 선정한다.
추정된 모형이 타당한지를 검토하기 위해 잔차 분석을 실시한다.
회귀모형 및 계수들의 유의성이 입증된 후 추정된 회귀식을 통하여 모형을 해석하고, 독립변수의 값에 따른 종속변수의 값을 예측할 수 있다(유성모 외 1인, 2006).
ALC라는 용어는 1950년대 말 유럽의 기술이 일본으로 도입될 때 일본에서 만들어진 용어로서 현재 일본, 한국, 말레이지아, 인도네시아, 대만, 태국등 주로 동남아시아에서만 사용되고 있다. 그 이외의 전 세계국가에서는 AAC라는 용어를 사용하고 있으며, ALC가 본격적으로 개발, 일반화된 독일에서는 현재 Porenbeton이라는 용어를 사용하고 있다. 또한 유럽의 일부 국가에서는 Cellular Concrete로도 불리 워 지고 있다. ALC는 혼화제와 같은 화학물질로 콘크리트 내 기포를 생성하여 자연 양생한 기포콘크리트 (Foam Concrete) 와는 전혀 다른 별도의 제품이다(http://www.alc.or.kr).
북유럽의 국가들은 한 냉한 기후조건에 따라 우수한 단열성능과 시공 상 기후제약요소가 적은 건축자재의 필요성에 맞춰 개발되어 사용되다가 건축현장 에서 본격적으로 보급되기 시작한 것은 2차 세계대전 후 전후복구사업을 위해 1945년부터 독일의 Josep Hebel에 의해 Hebel사가 설립된 후 부터다. 그 이후 주변 유럽국가로 보급되었으며, 품질 및 생산설비의 개발이 꾸준히 발전되어 현재 전 세계 50여 개국에서 사용되고 있다. 일본은 동경대지진 이후 내지진성 및 내화성이 탁월한 건축자재의 필요성에 맞춰 1960년대 초 유럽의 기술을 전수받아 생산해오고 있으며, 특히 조립식부재인 ALC패널공법을 집중 개발하여 고베 지진 시 ALC건축물의 탁월한 내진성이 입증된 바 있다(http://www.alc.or.kr)).
ALC (Autoclaved Lightweight Concrete) 는 발포제에 의하여 콘크리트 내부에 무수한 기포를 독립적으로 분산시켜 중량을 가볍게 한 기포콘크리트의 일종으로 블록과 사전에 철근이 보강된 패널형태로서 생산되고 있다. ALC는 석회질, 규산질 원료와 기포제 및 혼화제를 주원료로 물과 혼합하여 슬러리를 만든 후 고온고압(180℃, 10Kg/㎠)의 오토클레이브(Autoclave)에서 증기양생 과정을 거쳐 구조적으로 안정된 판상구조(板狀構造)의 토벌모라이트(Tobermorite)결정을 이루는 과정으로 제조된다.
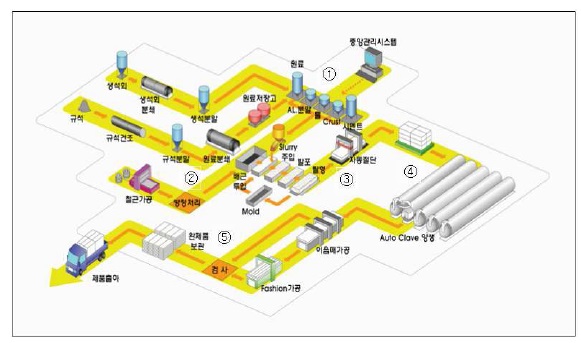
(1) <그림 2> ALC 제조공정도의 공정별 내용은 다음과 같다.
① 원재료배합
기본적인 원료는 물과 배합되어 슬러리(Slurry)형태로 되며, 여기에 소량의 알루미늄 분말을 첨가한다.
② 철근배근 및 타설
패널의 강도 유지를 위해 철근이 배근되며 방청처리 후 몰드에 세팅하여 원료슬러리가 타설된다.
③ 절단
몰드속의 슬러리가 충분히 경화되면 몰드를 해체시킨 후 절단공정으로 이동, 절단기기에 의해 필요한 규격으로 절단된다.
④ 증기양생
절단이 완료된 제품은 고온고압 양생기로 이동하여 고온고압으로 증기양생을 거치게 된다.
⑤ 품질검사 및 출하
증기양생 완료 후 양생 기에서 나온 제품은 품질관리 검사를 한 후 포장하여 출하한다((주)성은, 2000).
3.3.1 내화성
ALC는 무기질 소재로 불에 타지 않으며 화재 시에도 유독가스가 발생하지 않아 고층건물이나 대단위 아파트 등 안정성이 강조되는 건축물의 내·외장재로 적합하다.
3.3.2 단열성
ALC는 제품 내부에 포함되어있는 70%의 미세한 독립기포가 열의 전도를 강력하게 차단하므로 일반 콘크리트보다 10배 이상의 단열효과가 있어 보다 쾌적한 생활환경을 창출한다.
3.3.3 경량성
목재와 거의 같은 중량의 ALC(비중 : 0.5)는 일반 콘크리트 무게의 4분의 1 정도로 가벼워 건물전체의 경량화와 함께 시공효율, 인력절감 등 경제적 이익이 보장되는 초경량의 미래형 건축자재이다(http://www.syc-alc.co.kr).
3.3.4 차율성
ALC는 가벼우면서도 차음성과 흡음성이 뛰어나 소음이 심한 도심지의 오피스빌딩이나 주거용 건물 등의 내·외벽재로 좋다. 특히, 석고보드 등 다른 자재와 조합하여 사용하면 그 효과를 높일 수 있다.
3.3.5 평활성
ALC만의 특수공법(진동절단)으로 생산, 사인펜으로 글씨를 쓸 수 있을 정도로 표면이 평활하다. 이 평활성은 건물의 내구성에 큰 영향을 끼치는 방수제나 외벽 마감재의 부착성을 높이며, 이외에도 건물내부를 간단히 시공했을 경우에 분가루의 떨어짐이 적어 내장 마감재의 선택과 도색작업 등에 따른 비용을 훨씬 절감할 수 있다.
3.3.6 시공성
ALC는 가벼우면서도 목재와 같이 쉽게 절단 가공되므로 시공이 간편하고 제품의 규격화와 표준화와 건식공법에 의한 시공으로 공사기간의 단축은 물론 공사비용도 대폭 절감 할 수 있는 자재이다(http://www.syc-alc.co.kr).
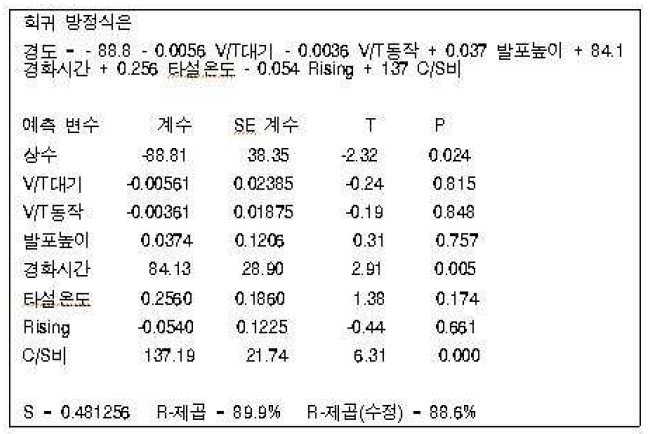
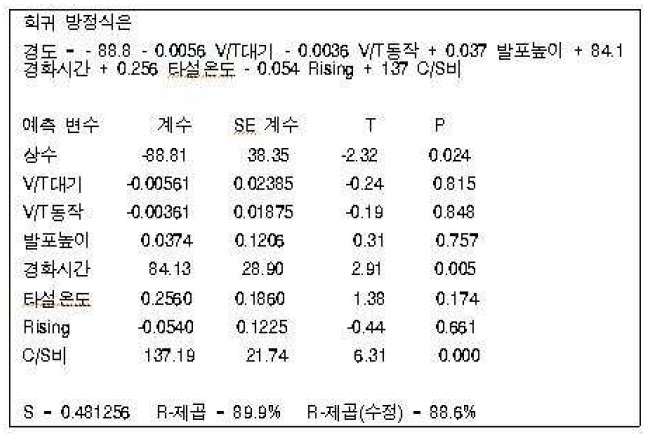
다중 회귀분석 결과
<표 4>의 다중 회귀분석 결과에서 회귀 계수의 유의성을 보면 경화시간, C/S비는 p-값이 0.005, 0.000으로 유의하게 나타났으며 V/T대기, V/T동작, 발포높이, 타설 온도, Rising은 p값이 각각 0.815, 0.848, 0.757, 0.174, 0.661로 유의수준 0.05보다 크므로 유의하지 않은 결과가 나왔다.
ALC 제조공정 경도 실험에 대하여 추정된 회귀 방정식은 경도 = - 88.8 - 0.0056 V/T대기 - 0.0036 V/T동작 + 0.037 발포높이 + 84.1 경화시간 + 0.256 타설온도 - 0.054 Rising + 137 C/S비이다.
4.2.1 결정계수 R2와 수정 결정계수 R2
회귀 제곱 합이 전체 제곱 합에서 차지하는 비율을 결정계수라고 하며
결정계수의 범위는 0과 1 사이의 실수이며 결정계수의 값이 1에 가까울수록 현재 고려하고 있는 다중 선형회귀모형의 독립변수들에 의하여 종속변수의 변동이 설명되는 설명력이 크다는 것을 의미한다.
4.2.2 분사눈석표의 F-검정
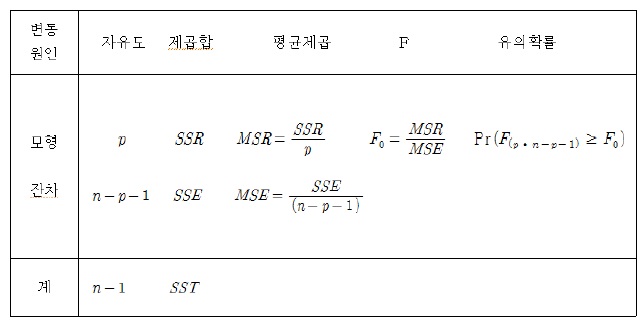
분산분석표는 종속변수의 전체 변동을 나타내는 총 제곱 합을 회귀 제곱합과 오차 제곱 합으로 분해하고 그들의 관계를 정리한 표이다. 회귀계수에 대한 유의성 검정을 통하여 각 독립변수가 종속변수를 설명하는데 유의한지를 검정할 수 있으며, 더 나아가 분산분석표를 통하여 현재 연구자가 고려하고 있는 회귀모형 자체의 유의성을 검정하는 것이 가능하다(박성현, 2005).
4.2.3 귀무가설과 대립가설 정의
4.2.4 유의수준
유의수준을 0.05로 정한다.
4.2.5 p-값 산출
설명변수와 반응변수의 관계를 설명하기 위하여 설정한 다중 선형회귀모형이 과연 타당하며 그 관계를 어느 정도 충분히 설명하고 있는지를 살펴보기 위하여 전체 변동을 나타내는 전체 제곱 합을 회귀 제곱합과 오차 제곱 합으로 나누고 그의 관계를 정리한 <표 5>가 분산분석표(Analysis of Variance Table)이다.
다중 회귀모형에서도 역시 MSR이 MSE 보다 상대적으로 충분히 크면 다중 회귀모형이 독립변수와 종속변수 사이의 관계를 설명하는데 유의하다고 판단한다.
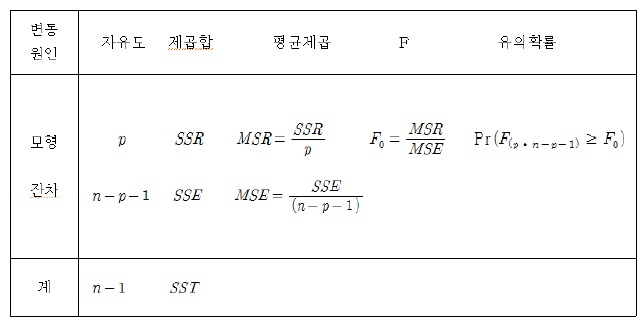
분산분석표
4.2.6 귀무가설(H0)의 기각 여부 결정
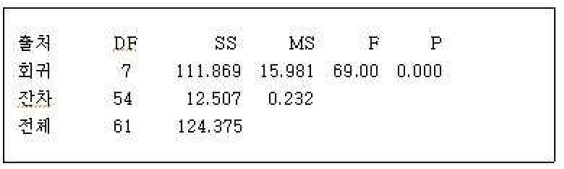
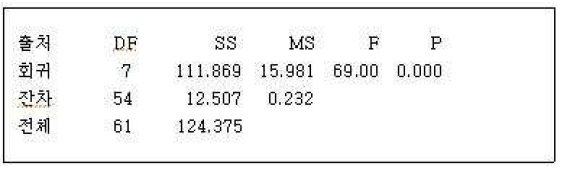
분산분석 결과
<표 6> 분산분석 결과 p-값이 0.000으로 회귀식이 유의하다고 할 수 있다.
결과적으로 ALC 제조공정 경도 실험에 대한 다중 회귀분석결과 모형 자체는 유의하지만 독립변수 중 경화시간, C/S비를 제외한 나머지는 추정된 회귀계수가 유의하지 못하므로 다중회귀모형에 포함시키는 것은 무리가 있다.
이러한 문제점을 해결하기 위해서 최량부분적합과 단계적 회귀분석을 수행하였다.
4.3.1 전진 선택법 (Forward Selection Method)
전진 선택법의 첫 단계에서는 상수항만으로 이루어진 모형으로부터 시작하여 추가되는 설명변수에 대한 회귀계수의 통계적 유의성에 대한 검정통계량 T-값(또는 부분 F-값)을 가장 크게 하는 변수 하나를 찾는다. 그 변수를 X(1)이라고 하자. 이때 X(1)에 관한 부분 F-검정에 대한 p-값이 유의수준
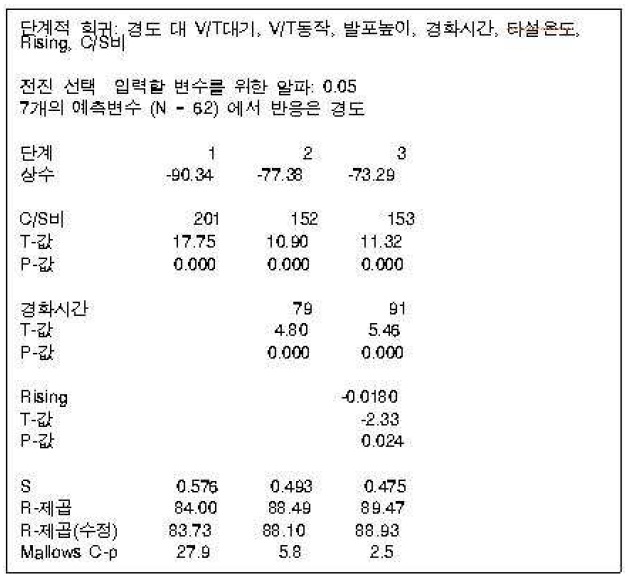
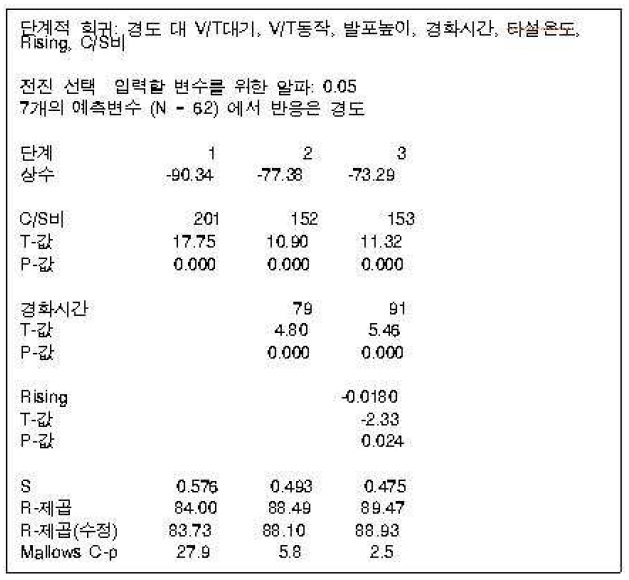
단계적 회귀분석 ?전진 선택법 결과
ALC 제조공정 경도 실험에 대하여 3단계에 걸쳐 전진 선택법(Forward Selection Method)을 진행시켰다. 여기서 주의 깊게 볼 것은 P-값으로 이 값이
1단계에서는 상수항과 C/S비가 회귀모형에 포함된다. R-제곱이 84.00%이다. 2단계에서는 경화시간이 회귀모형에 추가로 포함되었으며 R-제곱이 88.49%이다. 3단계에서는 Rising이 회귀모형에 추가로 포함되어 R-제곱이 89.47%이다. R-제곱(수정)은 83.73%에서 88.93%로 5.2% 증가하였다.
Mallows C-p 통계량은 적합치의 평균 제곱 오차와 관련이 있으며, 일반적으로 Mallows C-p가 작은 값이면 모형이 실제 회귀계수를 추정하고 미래 반응 값을 예측하는데 있어서 비교적 정확하다(분산이 작다)는 것을 나타낸다(유성모 외 1인, 2006).
결과적으로 7개의 예측변수에 대해 전진 선택법을 수행한 결과 C/S비, 경화시간, Rising만이 유의한 예측변수로 선택되었다.
4.3.2 후진 제거법(Backward Ellrnlnation Method)
후진 제거법의 첫 단계에는 완전모형으로 시작하여 하나의 변수가 제거되었을 때 부분 F-값이 가장 작은 변수를 찾는다. 그 변수를 X(k)이라고 하자.
이때 X(k)에 대한 F-검정의 p-값이 유의수준
두 번째 단계에서는 첫 단계에서 제거된 X(k)을 제외한 회귀모형에서 또 하나의 변수가 제거되었을 때 부분 F-값이 가장 작은 변수를 찾는다.
이 변수에 관한 부분 F-검정의 p-값이 유의수준
이와 같은 과정은 제거될 설명변수에 대한 부분 F-검정의 p-값이 유의수준보다 작을 때까지 반복한다(유성모 외 1인, 2006).
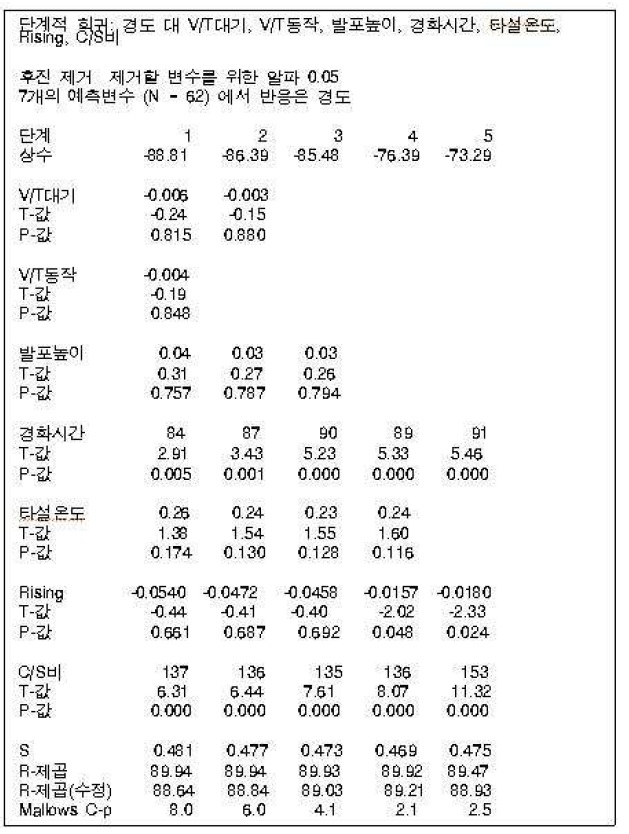
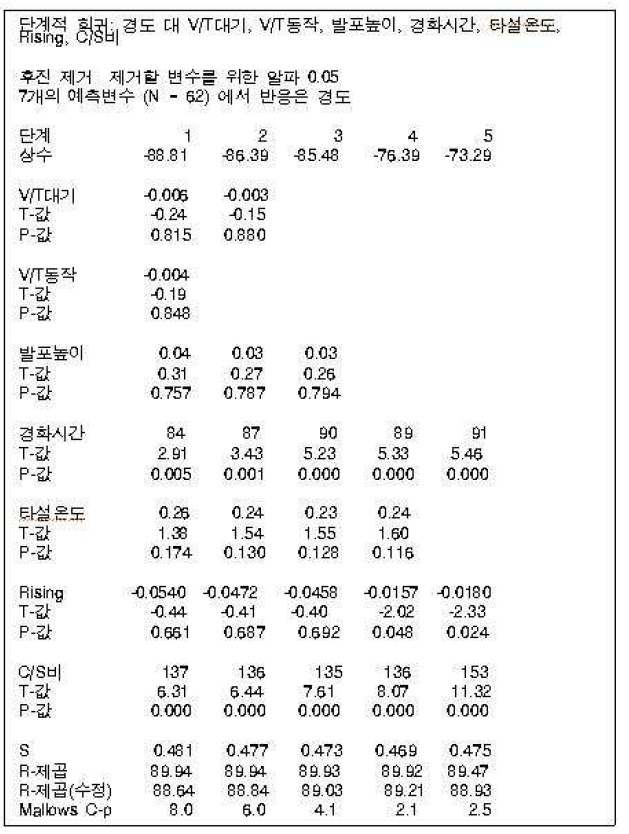
단계적 회귀분석 ? 후진 제거법 결과
ALC 제조공정 경도 실험에 대하여 5단계에 걸쳐 후진 제거법 (Backward Elimination Method)을 진행시켰다.
1단계의 모형은 상수항과 V/T대기, V/T동작, 발포높이, 경화시간, 타설온도, Rising, C/S비 모두 들어가는 모형이다.
2단계에서는 p-값이 가장 큰 V/T동작이 제거되었다.
3단계에서는 V/T대기가 p-값이 크기 때문에 제거된다.
4단계에서는 발포높이의 p-값이 0.794로 가장 크기 때문에 제거되었다.
마지막 5단계에서는 타설 온도의 p-값이 0.116으로 가장 크기 때문에 제거되고 나머지 예측변수들의 p-값이 유의수준 (
따라서 5단계에서 끝이 나고 그 때의 R-제곱은 89.47%, R-제곱(수정)은 88.93%이다.
결과적으로 7개의 예측변수에 대해 후진 제거 법을 수행한 결과 경화시간, Rising, C/S비만이 유의한 예측변수로 선택되었다. 이 결과는 앞서 전진 선택법을 이용하여 변수 선택을 했을 때와 동일한 결과이다.
최량 부분 집합에서는 예측변수로 가장 적합도가 높은 회귀 모형을 찾아낸다.
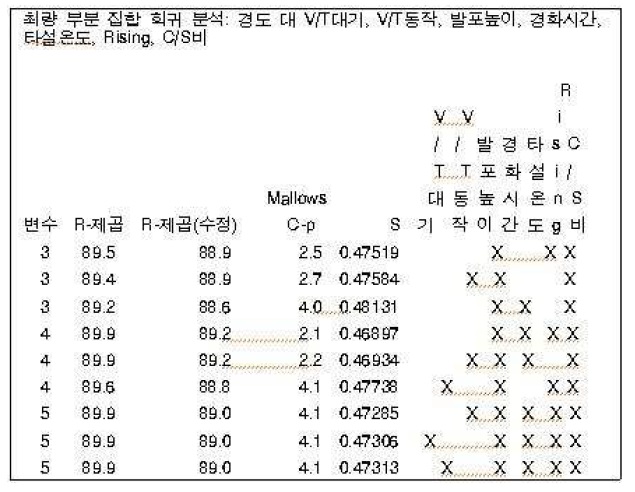
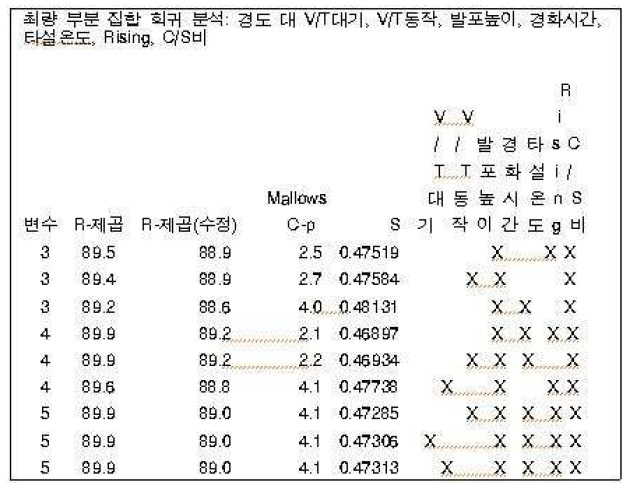
최량 부분 집합 결과
<표 9>는 최량 부분 집합 회귀 분석 결과로 모형별 자유 예측 변수 최소를 3으로, 모형별 자유 예측변수 최대를 5로 지정하고 출력할 각 크기의 모형을 3으로 설정하여 출력된 결과 값이다.
결과 값을 분석하기 위해 최량 부분 집합 모형 선택에 근거가 되는 통계량으로는 예측변수 수가 동일할 때는 R-제곱 값이 큰 모형을 선택한다. 예측변수 수가 다른 모형들과 비교할 때는 R-제곱(수정) 값이 큰 것을 선택한다.
일반적으로는 Mallows C-p가 예측변수의 수와 비슷하면서 작은 모형을 선택한다.
S는 회귀모형의 적합도를 측정하는 기준이 되는데 그 값이 작을수록 모형의 적합도가 좋다는 의미이다.
ALC 제조공정 경도 실험의 결과 예측변수가 3개인 경우 경화시간, Rising, C/S비를 포함한 모형이, 예측변수가 4개인 경우는 경화시간, 타설 온도, Rising, C/S비를 포함한 모형이, 예측변수가 5개인 경우는 발포높이, 경화시간, 타설온도, Rising, C/S비를 포함한 모형이 가장 좋게 나왔다.
예측변수 3, 4, 5를 비교하면 R-제곱 89.9%인 4, 5변수 중 R-제곱(수정) 89.0%보다 큰 89.2%의 예측변수 4개인 경우의 변수모형을 선택하며, 동일 변수 중 Mallows C-p값이 2.2보다 작은 2.1, S값이 0.46934보다 작은 0.46897로 적합도가 좋은 4개의 예측변수 경화시간, 타설온도, Rising, C/S비의 모형을 최종 모형으로 선택하였다.
선택된 모형이 타당한지를 검토하기 위해 회귀 분석과 잔차분석을 실시하였다.
4.5.1 회귀 분석
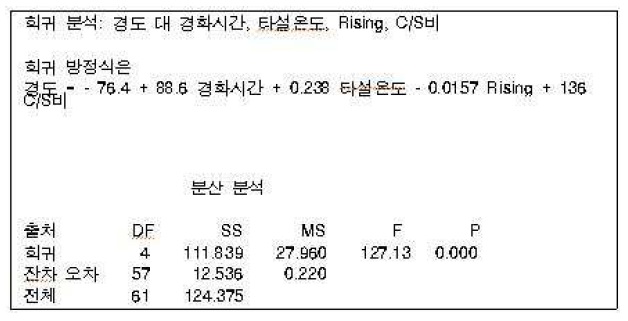
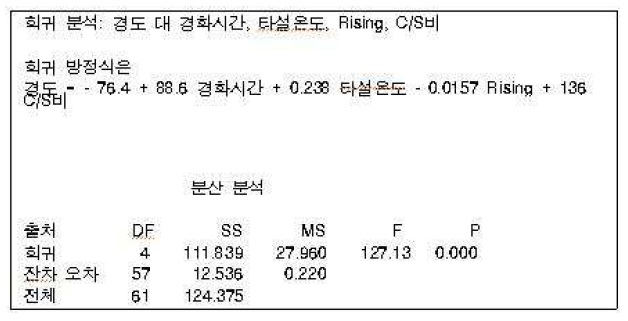
최종 모형의 회귀분석 결과
최종 모형의 회귀 분석 결과는 아래 <표 10>과 같다.
선택된 변수로 추정된 회귀 식을 보면 경도 = - 76.4 + 88.6 경화시간 + 0.238 타설온도 - 0.0157 Rising + 136 C/S비로 회귀모형이 적합 되었고, 분산분석표의 p-값을 보아도 모형자체가 유의하다.
4.5.2 잔차 분석
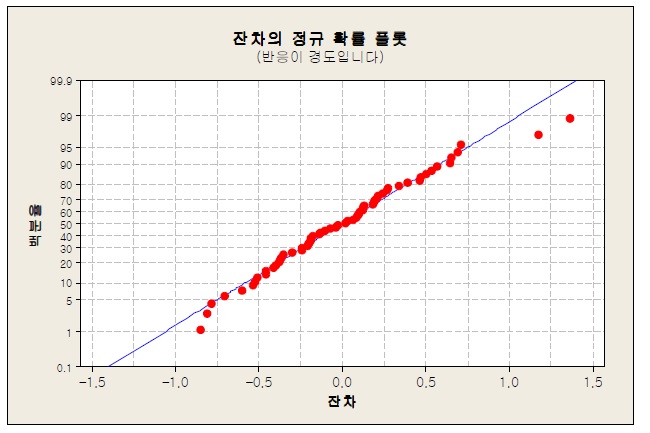
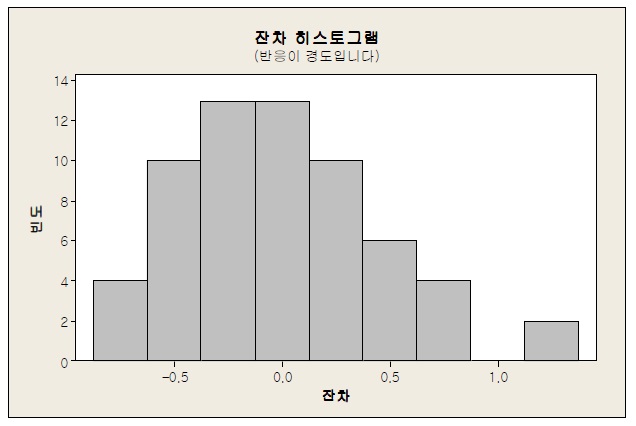
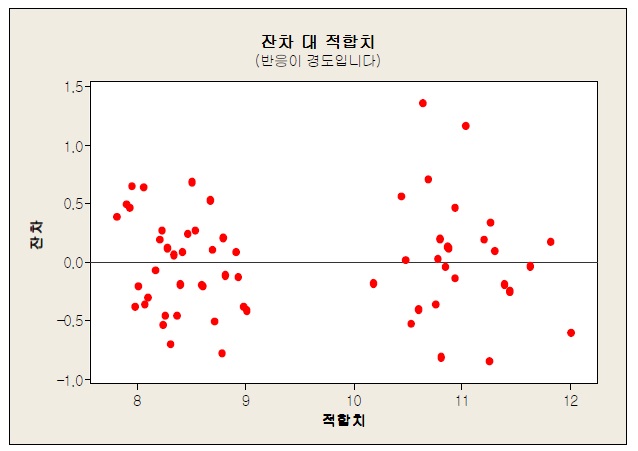
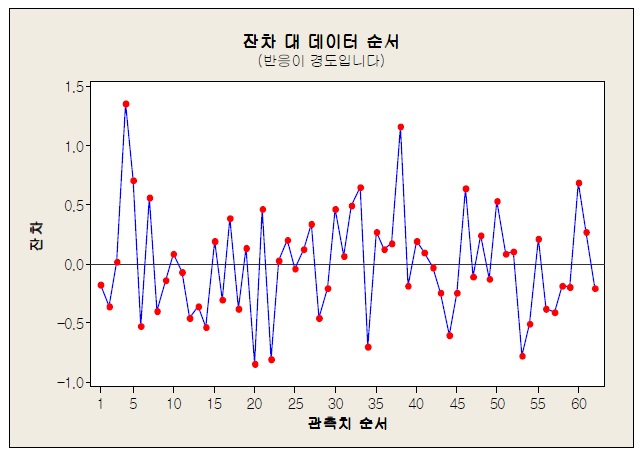
다중 회귀모형에서 필요로 하는 잔차 분석 결과는 <그림 3>~ <그림 6>와 같다.
<그림 3>, <그림 4>는 잔차 정규 확률도에서 데이터가 직선에 가까우므로 정규분포를 따른다고 볼 수 있다.
<그림 5>을 통해 잔차 등분산성을 알아볼 수 있다. <그림 5>의 경우 어떠한 규칙이나 패턴을 보이지 않고 랜덤으로 분포되어 있으므로 등분산성도 만족되었다고 볼 수 있다.
<그림 6>을 통해 잔차 독립성을 알아볼 수 있다. <그림 6>에서는 특정한 패턴을 보이지 않으므로 잔차 독립성이 만족되었다고 할 수 있다.
본 연구에서는 ALC 제조공정 중 예비양생이 완료된 반 경화제품(cake) 탈 형 시기의 관리기준이 되는 경도에 관한 예측을 하기 위해 관련된 변수들 간에 상호관련성을 찾고자 다중회귀분석을 이용한 연구를 진행하여 다음과 같은 결론을 얻었다.
1) 7개의 독립변수 조건에 따른 62개의 실험 데이터에 대하여 다중 회귀분석을 실시한 결과 추정된 회귀방정식은 경도= - 88.8 - 0.0056 V/T대기 - 0.0036 V/T동작 + 0.037 발포높이 + 84.1 경화시간 + 0.256 타설온도 - 0.054 Rising + 137 C/S비로써 회귀 계수의 유의성을 보면 경화시간, C/S비는 p-값이 0.005, 0.000으로 유의하게 나타났으며, V/T대기, V/T동작, 발포높이, 타설온도, Rising은 p-값이 각각 0.815, 0.848, 0.757, 0.174, 0.661로 유의수준 0.05보다 크므로 유의하지 않은 결과가 나왔다.
회귀모형의 설명력은 R-제곱이 89.9%, R-제곱(수정)값이 88.6%로써 설명력이 높게 나타났으며, 분산분석 결과 p-값이 0.000으로 회귀식이 유의하다고 할 수 있었다.
2) 7개의 예측변수에 대해 전진 선택법을 수행한 결과 C/S비, 경화시간, Rising만이 유의한 예측변수로 선택되었다. 1단계에서는 상수항과 C/S비가 회귀모형에 포함되어 R-제곱이 84.00%, 2단계에서는 경화시간이 회귀모형에 추가로 포함되어 R-제곱이 88.49%, 3단계에서는 Rising이 회귀모형에 추가로 포함되어 R-제곱이 89.47%로 나타났다.
R-제곱(수정)은 1단계 83.73%에서 3단계 88.93%로 5.2% 증가하였다.
Mallows C-p 통계량은 1단계 27.9에서 3단계 2.5로 작은 값일수록 실제 회귀계수를 추정하고 미래 반응 값을 예측하는데 있어서 비교적 정확함을 나타내었다.
3) 후진제거 법 수행 결과 5단계에서 끝이 나고 7개의 예측변수 중 경화시간, Rising, C/S비만이 유의한 예측변수로 선택되었다.
R-제곱은 89.47%, R-제곱(수정)은 88.93%로 전진 선택법을 이용하여 변수 선택을 했을 때와 동일한 결과를 얻었다.
4) 최량 부분 집합 회귀 분석 결과에서는 R-제곱 89.9%, R-제곱(수정) 89.2%, Mallows C-p값이 2.1, S값이 0.46897인 4개의 예측변수 경화시간, 타설 온도, Rising, C/S비의 모형을 최종 모형으로 선택되었다.
5) 최종 모형으로 선택된 모형이 타당한지를 검토하기 위해 회귀 분석과 잔차 분석을
실시한 결과 추정된 회귀 식은 경도 = - 76.4 + 88.6 경화시간 + 0.238 타설 온도 - 0.0157 Rising + 136 C/S비로 회귀모형이 적합 되었고, 분산분석의 p-값 0.000으로 모형자체가 유의함을 나타내었다.
잔차 분석 결과 잔차 정규 확률지에서 데이터가 직선에 가까운 정규분포를, 잔차 대 적합지 에서는 규칙이나 패턴을 보이지 않고 랜덤으로 분포되어 등분산성을 만족 시켰으며, 잔차 대 데이터 순서 그래프는 특정한 패턴을 보이지 않은 잔차의 독립성을 만족 시켰다.
본 연구는 ALC 제조공정 전체가 아닌 탈형 및 절단 공정에서 탈형 시기의 기준이 되는 경도에 관한 다중 회귀분석을 수행한 제한적 연구로 진행되었지만 향후 ALC의 대중 보편화를 위해서라도 ALC에 관한 많은 연구가 필요하다.