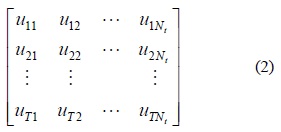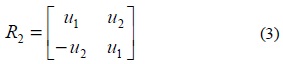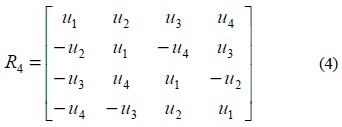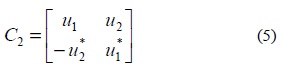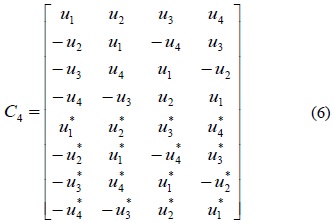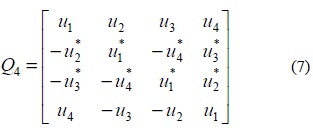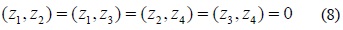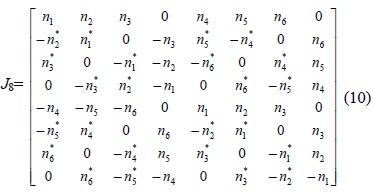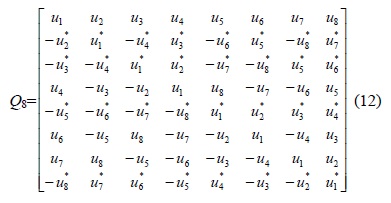본 논문은 최대 32개의 송수신 안테나를 사용하는 준직교 공간시간 블록부호 (QOSTBC) 를 적용한 대규모 MIMO 시스템을 제안한다. QOSTBC 는 전송율 및 복호 복잡성에 있어서 장점을 가지고 있으며 2개 이상의 송수신 안테나를 적용한 MIMO 시스템에서는 중요한 전송다이버시티 기술이다. 대규모 MIMO 는 매우 많은 송수신 안테나를 적용한 MIMO 시스템이며 최소한 15개 이상의 안테나를 적용하여야 한다. 본 논문은 다양한 안테나 구성 (2x2, 4x4, 8x8, 16x16, 32x32) 으로 QOSTBC를 적용한 대규모 MIMO 를 제안하며 BPSK 변조를 적용하여 성능을 분석하였다. 기존 대규모 MIMO 시스템과 비교하여 QOSTBC를 적용한 대규모 MIMO 에서는 송수신 안테나 개수 증가에 따른 다이버시티 이득이 증가하면서 높은 성능 개선 효과를 확인할 수 있었다.
As mobile communication systems evolve, higher transmission data rate, higher spectral efficiency and higher reliability requirements have been an important issue. To meet these requirements, massive multipleinput multiple-output (MIMO) technology has become an attractive field of research and massive MIMO can be built with inexpensive, low-power components [1]. Massive MIMO communication is widely considered to be an appropriate to achieve much higher bandwidth efficiency and improve the performance reliability of modern wireless communication [2]. The massive MIMO transmission of signal processing is performed in time and spatial dimensions by utilizing multiple, spatially distributed antennas at both transmitting and receiving sides.
In addition, combining with space-time codes (STC) [3], the usage of multiple antennas offers not only enormous spectral efficiencies but also a significant improvement in system performance. STC techniques such as Alamouti’s space-time block code (STBC) that combine coding, modulation and signal processing in wireless communication, have been used to achieve spatial diversity and improve the bit-error rate (BER) performance [4-6]. The transmit diversity scheme proposed by Alamouti [7] is a simple and effective orthogonal space-time block codes (OSTBCs or STBCs) of the full rate with two transmit antennas for the system. OSTBCs [8] based on orthogonal design are the most interesting schemes among space-time codes. They can significantly improve signal quality in quasi-static MIMO channel due to their full-diversity property.
Unfortunately, for more than 2 transmit antennas, the rate of the OSTBC [9], defined by the number of symbols transmitted divided by the number of time slots used by the OSTBC, cannot be larger than 3/4 [10]. However, we can achieve the rate larger than 3/4 for more than 2 transmit antennas using Quasi-Orthogonal STBC (QOSTBC) methods [11]. The QOSTBC is a very attractive transmit diversity scheme in terms of rate and decoding complexity. In [12], however, the number of transmit antennas for a rate-one QOSTBC was limited to 8. For massive MIMO systems, however, the number of antennas must be larger than at least 15. Therefore, a more thorough investigation in a true massive MIMO configuration with a large number of antennas still needs to be reported.
In this paper, we present a true massive MIMO with a large number of transmit and receive antennas up to 32 and perform comparative evaluation over different configurations. The main idea of increasing antennas is to increase the capacity with increasing error performance, i.e. decreasing BER. Therefore, we focus on BER reduction with full rate for a large number of antennas.
The rest of the paper is organized as follows. We explain about the massive MIMO system model in Section 2. The space-time block code is discussed in Section 3. Section 4 describes quasi-orthogonal spacetime block code. In Section 5, simulation results are presented. Finally, conclusions are drawn in Section 6.
Recently, massive MIMO systems, or large-scale antenna systems, have been investigated as new cellular network architecture for next generation high-speech wireless communications with several attractive characteristics. Massive MIMO can improve spectrum efficiency (SE), energy efficiency (EE) and reliability just by configuration massive antenna arrays at the existing base stations (BSs), which has been seen as a promising technology for future wireless communication systems [13]. This great potential of massive MIMO has stimulated great interest from both academics and industry.
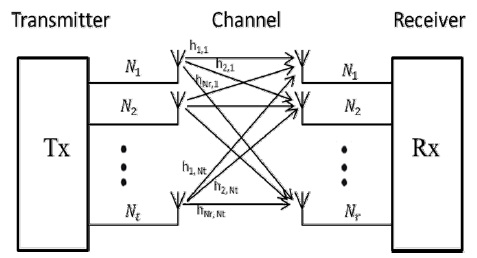
Let Nt denote the number of antenna elements at the transmitter, and Nr the number of antenna elements at the receiver. The channel with Nr outputs and Nt inputs is referred to a Nr×Nt matrix. The MIMO system model can be represented as
where
The term STBC, in general, is used to describe transmission schemes capturing these high data rates attainable by MIMO channels [14]. The STBC matrix has columns equal to the number of the transmit antennas and rows equal to the number of the time slots required to transmit the data. The STBC is represented by a matrix, where
where uij denotes information data symbol transmitted at time slot
In complex ODs, both the information symbols and their conjugates are utilized. The ith column of the code matrix can contain either the information symbols u1 ,⋯, uT , or their conjugates u1* , ⋯, uT* only. The space-time block code proposed by Alamouti [7] uses the complex orthogonal design. Orthogonal structure of code matrix of Alamouti scheme expressed in (5) achieves full-rate and full diversity.
Here, two time slots are required to transmit two symbols. Thus,
Ⅳ. Quasi-Orthogonal Space-Time Block Code
Alamouti code provides the full rate with full diversity for two antennas. Although Alamouti code can be further generalized for more than two antennas by using the concept of orthogonal designs, unfortunately, it does not provide any coding gain nor achieve a rate larger than 3/4 [16]. It is also proved in [17] that a complex orthogonal design and corresponding STBC which provide full diversity and full transmission rate is not possible for more than two antennas. Alamouti scheme is the only example of a full-rate full-diversity complex STBC using orthogonal designs.
QOSTBC is a full rate STBC for more than two transmit antennas. To design full rate codes with complex constellation, we consider codes with a decoding pair of symbols [17]. Such non-orthogonal codes for the 4 transmit antennas given in equation (7) are called QOSTBC.
In this code matrix column 1 and 2 as well as columns 3 and 4 are orthogonal to each other. We represent the ith column of above matrix by zi . Then, for any intermediate variable u1 , u2 , u3 , u4 , we have
In (8), subspace created by
Although Jafarkhani [17] built the transmission matrix for 8 transmit antennas from 4 antennas, the 8x8 matrix cannot provide more than rate code. For example, we compare two quasi-orthogonal STBCs with different rates for eight transmit antennas. The Jafarkhani QOSTBC for 8 transmit antennas (Nt) to send 6 information symbols (
The rate R of this QOSTBC code is,
The proposed design of transmission matrix for the same transmit antennas is shown in (12). This matrix is clearly a QOSTBC and sends
The BER performance of QOSTBC in massive MIMO is evaluated through simulations and the results are discussed in the next section.
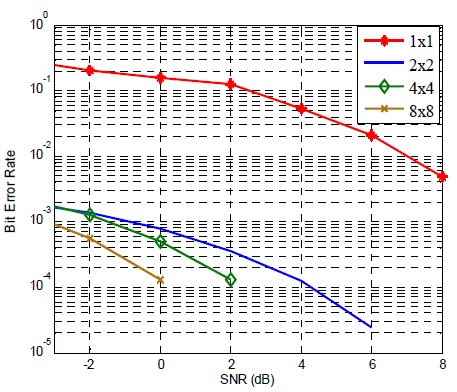
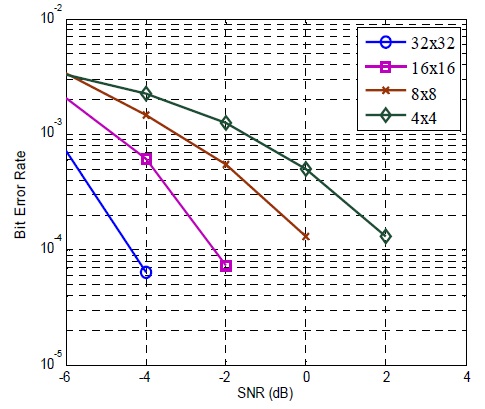
In this section, computer simulations are conducted to investigate the BER performance of the massive MIMO system. When we increase the QOSTBC matrix size (see in (12)), we evaluate the BER performance according to the matrix size (i.e., the number of antennas). It should be noted that for increasing the number of antennas, the STBC code should be matched to the antenna number. In the simulation, we increased the number of antennas up to 32, by designing the QOSTBC code into the size of 32×32. In order to examine the BER performance, the massive MIMO system using QOSTBC with 1×1, 2×2, 4×4, 8×8, 16×16 and up to 32×32 number of antennas is implemented and the results are shown in Figs. 2 and 3.
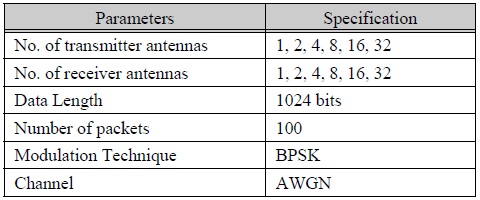
In this simulation, the modulation used is BPSK and the total transmit signal power was equally divided by the number of antennas. The channel is assumed to be an Additive White Gaussian Noise (AWGN) channel. The results are observed with the assumption that the channel state information is perfectly known to the receiver. The parameters used in the simulation are shown in Table 1.
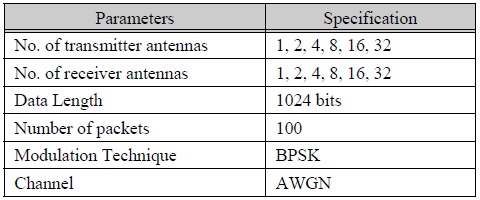
시뮬레이션 파라미터
Simulations are carried out for evaluating performances with different SNR values. Figs. 2 and 3 show a significant performance improvement when the number of transmit and receive antennas increases. Also, a greater performance improvement is observed with increased SNR.
Fig. 2 shows BER performance of the massive MIMO using QOSTBC with 1×1, 2×2, 4×4 and 8×8 number of antennas. As can be seen in Fig. 2, increasing the number of antennas results in significant BER performance. In case of higher SNRs, BER decreases drastically. It is important to note that the performances of massive MIMO increase with a higher number of transmit and receive antennas. This is due to diversity from a large number of transmission paths deliberately created. In the 8×8 configuration, the BER performance shows nearly 10-4 at a SNR value of 0dB.
Fig. 3 illustrates the comparison of the BER performances of massive MIMO with 4×4, 8×8, 16×16 and 32×32 number of transmit and receive antennas using QOSTBC. The BER performances increase as more antennas at both sides are employed. The best BER performance is achieved with the 32×32 configuration as expected. Therefore, it can be said that an increasing number of antennas in massive MIMO provide significant increase in diversity gain and subsequently BER improvement.
We have presented the BER performance of massive MIMO systems with up to 32×32 antenna configuration using QOSTBC. The performances are compared with a different number of transmit and receive antennas under the BPSK modulation scheme. Simulation results for QOSTBC in massive MIMO show a consistent performance improvement with increasing number of transmit and receive antennas.
It is concluded that QOSTBC shows full rate and is an adequate modulation format for massive MIMO. The work for massive MIMO performance evaluation under fading conditions as well as with imperfect channel state information can be undertaken. In addition, a field test of the proposed system could be of interest as future works.