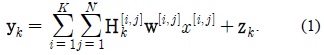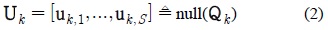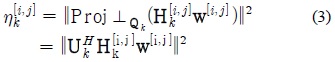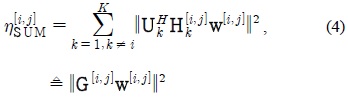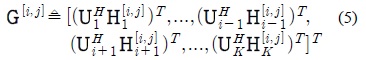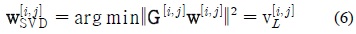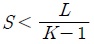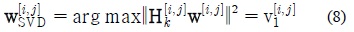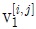최근 새롭고 다양한 멀티미디어 기기들이 등장함에 따라 무선 인터넷 통신의 수요가 급격하게 증가 하고 있다. 이렇게 늘어나는 트래픽 수요를 해결하기 위한 가장 효과적인 방법 중 하나는 스몰 셀 기술이다. 그러나 셀의 크기가 줄어들면 셀 간 간섭이 증가하여 이를 해결해야만 한다. 이러한 간섭 문제를 해결하기 위하여 다양한 연구들이 진행되어 왔다[1,2]. 그 중에서 간섭정렬 (interference alignment, IA) 기술은 기존의 간섭 관리 기법의 한계를 극복하고 사용자 간섭 채널의 최적자유도를 달성시키는 유망한 기술로서 학계와 산업계의 큰 관심을 받아 왔다[3,4].

간섭정렬 기반 간섭 제어 기법들 중 기회적 간섭정렬 (opportunistic interference alignment, OIA) 기술은 실제적으로 무선 시스템에 접목이 가능하고 이론적 성능뿐 아니라 시스템 전송률 측면에서도 탁월하다고 알려져 있다[5-8]. 기회적 간섭정렬은 간섭정렬과는 다르게 사용자 선택(스케줄링)이 포함된 기술로서 전체 네트워크의 채널 상태 정보를 필요로 하지 않으며, 시간과 주파수 확장 그리고 빔 형성 디자인의 반복이 필요 없으므로 기존의 간섭정렬보다 훨씬 구현하기 쉽다고 알려져 있다.

한편, 최근 IEEE 802.11ax 와 같은 차세대 무선 랜 네트워크에 대한 관심이 뜨겁다. 무선 랜 네트워크는 기본적으로 랜덤액세스 네트워크 (random acees network, RAN)라 볼 수 있다. 랜덤 액세스 네트워크는 각 사용자가 자신의 트래픽 전송을 분산적으로 결정하므로 동일한 네트워크 내에 존재하는 2명 이상의 사용자가 동시에 데이터를 전송할 경우 충돌을 발생한다. 이러한 패킷 충돌 문제를 해결하기 위하여 기지국(access point, AP)의 다중 안테나를 활용하는 방식이 고려되어 왔다[9-13]. 기지국의 다중 안테나는 추가적인 주파수 자원이나 표준의 변화를 요구하지 않아 매우 효과적인 성능향상 기법으로 평가된다. 최근 다중 안테나 기술을 단일 무선 랜 네트워크에 적용하는 것에서 벗어나 다중셀 무선 랜 네트워크에서 다중 안테나를 활용하여 성능을 향상시키려는 연구가 진행되고 있다[14]. 특히 차세대 무선 랜 네트워크로 알려져 있는 IEEE 802.11ax 표준에서는 인접한 무선 랜 네트워크에서의 간섭 문제를 해결하는 것이 매우 중요한 기술적 과제로 평가되고 있다[15]. 특히, 최근 기회적 간섭정렬 기술을 다중 셀 랜덤액세스 네트워크에 적용하면 기존의 네트워크 성능을 크게 향상시킬 수 있다는 사실이 밝혀졌다[16,17]. 제안된 다중 셀 랜덤액세스 네트워크용 기회적 간섭정렬 기술은 기존의 랜덤 액세스 네트워크의 기본적인 구조를 크게 바꾸지 않으면서 물리계층과 매체접근제어 계층을 보완하여 상용 시스템에도 효과적으로 적용될 수 있을 것으로 판단된다. 그러나 [16,17]에서 제안된 기회적 간섭정렬 기술은 인접 셀로 미치는 간섭의 양을 최소화하는 기법으로 자신의 셀 기지국에 도착하는 신호의 세기는 고려하지 않았다.

본 논문에서는 [16,17]에서 제안된 기회적 간섭정렬의 개념과 정반대로 자신의 신호세기를 최대화하는 기법을 고려한다. 또한 본 논문에서는 물리계층과 매체 접근제어계층을 동시에 고려한다. 물리계층에서는 특이 값 분해에 기반을 둔 빔 형성 기법으로 신호를 전송하고, 매체접근제어 계층에서는 사용자들의 기여 간섭을 오랜 시간 관찰하고 그를 통해 얻은 누적 분포 함수를 이용하여 특정한 임계값을 설정하여 이를 기준으로 사용자 선택이 이루어진다. 이 임계값은 사용자들의 패킷 전송 확률과 밀접한 관련이 있다. 본 논문에서는 기존의 간섭 최소화 기법과 본 논문에서 제안된 신호최대화 기법 사이의 상관관계에 관하여 자세히 살펴본다.

본 논문은 다음과 같이 구성된다. 제 2장은 시스템 모델을 소개하고 제 3장에서는 기존 기회적 간섭정렬기술과 본 논문에서 고려한 신호 최대화 기법을 비교한다. 제 4장은 3장에서 고려한 두 방식의 성능을 서로 다른 환경에서 비교하고 제 5장에서 결론을 맺는다.

본 논문에서는 각 하나의 액세스 포인트와 N명의 사용자가 존재하는 K개의 상향 링크 랜덤액세스 네트워크를 가정한다. 하나의 액세스 포인트는 M개의 안테나를 갖고 각 사용자는 L개의 안테나를 갖는다. 각 랜덤 액세스 네트워크는 시 분할된 ALOHA 프로토콜로 작동된다고 가정하고 매 타임 슬롯마다 사용자들은 패킷 전송할 확률 p를 가진다. 랜덤 액세스 네트워크의 특성상 동시에 여러 명이 패킷을 보내는 상황은 불가피하다. 이런 경우 간섭은 생길 수밖에 없다. i번째 RAN 에 있는 j번째 유저가 k번째 액세스 포인트로 향하는 채널행렬은 , i,k∈{1,...,K}, j∈{1,...,N}로 정의된다. k번째 액세스 포인트에서 받는 신호 y_k∈ℂ^M×L 는 다음과 같이 표현될 수 있다.

x^[i,j]∈ℂ 와 w^[i,j]∈ℂ^L×1 은 각각 정보 스트림과 전송 빔 형성 벡터를 나타낸다. z_k∈ℂ^M×1 은 k번째 액세스 포인트에서의 가우시안 잡음을 나타낸다. 기본적으로 모든 사용자들이 다중경로 페이딩 (Rayleigh fading)을 겪고, 한 사용자 당 한 개의 정보 스트림만 전송한다고 가정한다. 채널이득은 매 타임 슬롯마다 독립적으로 변하고 각 액세스 포인트는 파일럿 신호 등을 전송하여 무선 채널 상호성 (channel reciprocity)에 의해 사용자들이 채널을 추정 할 수 있다고 가정한다. 모든 사용자들의 전파 손실은 서로 같다고 가정한다.

신호공간에 대한 조건 때문에 간섭널링기법(Interference Nulling)은 자유도가 제한되고 실제 시스템에서 활용하는데 어려움이 있다 [7]. 이를 해결하기 위해 기회적 간섭 정렬에서는 S에 대한 제약이 없고 1부터 M까지 임의의 수로 신호 공간이 결정될 수 있다.

k번째 액세스 포인트는 간섭정렬을 위한 Q_k = [q_k,1,...,q_{k, M - S}]로 정의되는 간섭 공간을 미리 결정한다. 여기서 q_k,m∈ℂ^M×1 은 정규 직교 기저이고 1 ≤ k ≤ K 와 1 ≤ m ≤ M - S 을 만족한다. S∈{1,2,...,M}은 각 액세스 포인트에서 신호 공간의 차원을 나타낸다. Q_k가 주어지면 k번째 액세스 포인트는 이의 영 공간인

을 계산 할 수 있다. u_k,i∈ℂ^M×1 은 정규 직교 기저이며 사용자들에게 알려지는 벡터이다. 만약 S = M이면 U_k는 정규 직교 행렬이 된다.

i번째 랜덤 액세스 네트워크에 있는 j번째 사용자의 단위 놈(norm) 빔 형성 벡터를 w^[i,j]라고 가정하자. U_k와 로부터 i번째 RAN에 있는 j번째 사용자는 누설 간섭(leakage of interference, i.e., LIF)이라고 불리는 인접 셀로의 발생 간섭(generating interference)을 다음과 같이 계산할 수 있다.

i ∈ {1,2,...,K}, j ∈ {1,2,...,N} 이고 k ∈ {1,2,...,K} ╲ i ∈ {1,...i-1,i＋1,...,K}이다. Proj⊥_A(B)은 A의 영 공간에 대해 B를 투영시키는 것으로 정의한다. ( • )^H은 Hermitian operation을 의미한다. 누설 간섭은 k번째 액세스 포인트에서 받는 간섭 파워로 볼 수 있으며 간섭공간인 Q_k에 정렬되지 않는 간섭의 양을 의미한다.

특정 랜덤 액세스 네트워크에 있는 사용자가 다른 랜덤 액세스 네트워크로 가는 간섭을 완벽하게 제거하는 대신에 제안된 기회적 간섭정렬 기법은 다른 액세스 포인트로 가는 간섭들의 파워의 합을 최소화 시키는 빔형성 기법을 이용한다. 따라서 각 사용자들은 최적의 전송 빔 형성 벡터 w^[i,j]을 다음과 같은 방법으로 선택한다. 우선 다른 RAN으로 가는 누설 간섭들의 합은 다음과 같이 정의 된다.

G^[i,j]∈ℂ^(K-1)S×L은 다음과 같이 정의 된다.

G^[i,j]의 특이 값 분해를 G^[i,j] = Ω^[i,j]Σ^[i,j]V^[i,j]H라고 하면 Ω^[i,j]∈ℂ^(K-1)S×L 이고, V^[i,j]∈ℂ^{L× L}은 L개의 정규 직교 벡터의 열로 이루어져 있다. 또한 이다. 최적의 w^[i,j]를 선택하는 방법은

으로 하면 된다. 여기서 은 V^[i,j]의 L번째 열이다. 이렇게 선택을 취함으로써 의 결과를 얻는다.

k번째 액세스 포인트에서 신호를 받고 난 후, Q_k에 정렬된 간섭을 제거하기 위해 U_k가 곱해진다. 따라서 받은 신호는 다음과 같다.

앞서 말한 특이 값 분해를 이용한 빔 형성 기법으로 다른 랜덤 액세스 네트워크로 가는 간섭을 최소화 하긴 했지만, 여전히 액세스 포인트의 신호공간에는 잔여 간섭이 남아 있을 수 있다. 따라서 이 잔여 간섭을 더욱 줄이기 위해 MAC 계층에서 동작을 추가로 제안한다. 셀룰러 네트워크에서 제안된 기존의 기회적 간섭정렬 기법에서는 각 셀마다 전송 사용자의 수가 고정 되어 있다. 하지만 랜덤액세스 네트워크에서는 이 수가 확률변수가 된다.

각각의 사용자들은 매 타임 슬롯마다 자신이 인접 네트워크에 발생시키는 간섭의 양을 오랜 시간동안 관찰한다. 그리고 이 간섭들을 통한 누적 분포 함수를 형성하며 매 타임 슬롯마다 생성되는 간섭을 누적 분포 함수에 상응하는 값과 임계값을 비교하여 전송할지 말지를 판단한다. 이 임계값은 전송확률 p라고 놓는다. 다시 말하면 생성된 간섭을 통해 미리 확인된 누적 분포 함수에 대응하는 값을 취한다. 이 값이 p보다 작을 경우 패킷을 전송 한다.

각 랜덤 액세스 네트워크에서 총 사용자의 수(N)가 증가하면, 전송 확률 p는 패킷 충돌을 피하기 위하여 작아진다. p의 감소는 다른 랜덤 액세스 네트워크로 가는 기여 간섭을 줄인다. 그러므로 각 셀마다 총 사용자의 수가 증가하면 간섭이 감소하는 경향을 가진다.

앞서 기술한 기회적 간섭정렬 기법의 경우 다른 랜덤 액세스 네트워크로 가는 간섭을 최소화 시키는 방식으로 운영된다. 그러나 기회적 간섭정렬 기법의 물리계층에서 특이 값 분해를 이용한 빔 형성 기법을 사용 할 때 빔 형성 벡터를 V^[i,j]의 L번째 열을 선택한 것에 착안하여 신호를 최대화 시키는 방법도 생각해 볼 수 있다.

신호의 최대화 기법 역시 물리계기층과 매체접근제어계층 둘 다 고려한다. 물리계층에서는 앞서 말한 V^[i,j]의 첫 번째 열을 선택하여 빔 형성을 하는 방법이고, 매체접근제어계층에서는 간섭의 최소화에서 했던 방식과 동일하게, 의 누적분포함수를 이용하여 자신의 채널 이득 값을 오랜 시간 저장하여 누적분포함수를 만들고 가장 채널상황이 좋은 사용자를 선택하는 방식을 취한다.

본 장에서는 3개의 랜덤 액세스 네트워크와 각 네트워크에 10명의 사용자가 있다고 가정한다. 사용자들은 각각 3개의 안테나를 갖고, 하나의 네트워크에는 한 개의 액세스 포인트가 있으며 각 액세스 포인트에도 3개의 안테나가 존재한다고 가정한다. 신호 공간 S도 3이라 가정한다. 즉 K = L = M = S = 3, N=10이다. 채널행렬은 시간 축에서 독립적인 Rayleigh 페이딩을 가정한다. 기본적으로 모든 액세스 포인트에서 신호 대 잡음비(SNR)는 0dB라고 하자. 액세스 포인트들은 MIMO복호 방식으로서 Zero-Forcing 기법을 사용한다. 마지막으로 디코딩 성공확률의 기준으로 신호 대 간섭 및 잡음비(SINR) 역시 0dB로 가정한다.

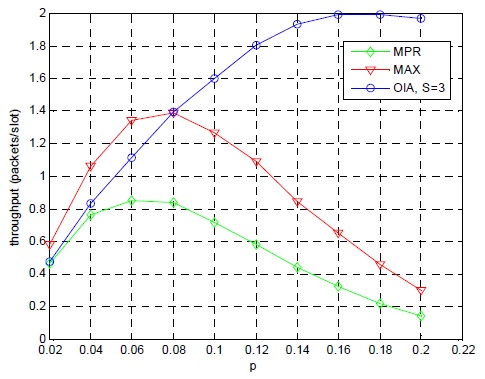
그림 1은 기존 multi-packet reception (MPR), 기회적 간섭정렬기법 (OIA), 본 논문에서 제안된 신호 최대화 기법 (signal maximization)의 시스템 전송률을 나타낸다. 그림에서 보는 바와 같이 기회적 간섭정렬 기법과 본 논문에서 제안된 신호 최대화 기법이 MPR 기법에 비해 월등히 높은 전송률을 달성한다.

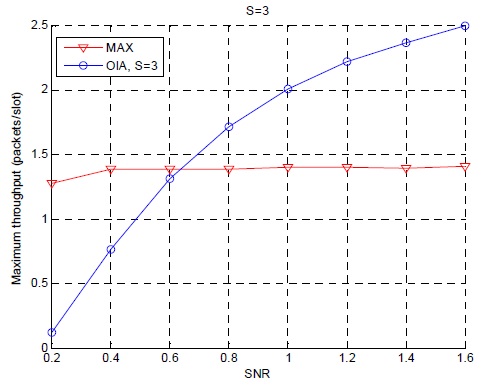
그림 2는 기회적 간섭정렬 기법과 신호 최대화 기법의 MAC 계층 전송률을 기준 신호 대 잡음비를 변화시키면서 비교하고 있다.

그림 2에서 보는 바와 같이 두 기법의 전송률은 신호대 잡음비의 변화에 따라 성능이 서로 뒤바뀐다. 대체적으로 신호 대 잡음비 변화에 따라 제안된 신호 최대화 기법은 크게 성능이 변화하지 않으나 기회적 간섭정렬기법의 성능이 크게 변화한다. 제안된 두 기술 모두 신호 대 잡음비가 약 0.63 (-0.2dB) 에서 1.38의 최대 처리율로 같다.

이 지점을 기준으로 트레이드오프가 발생한다. 이 지점 이후로는 기회적 간섭정렬 기법의 최대 전송률이 더 높다. 두 기법 모두의 성능은 최적 전송 확률 값이 적용된 결과이다.

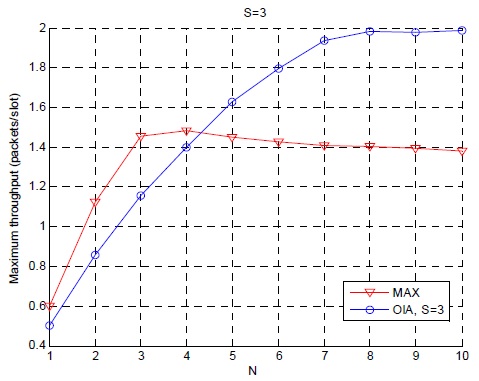
그림 3은 두 기법의 전송률 성능을 각 네트워크의 사용자 수에 따라 비교한 것이다. 여기서도 마찬가지로 두 기법의 성능이 서로 뒤바뀌는 것을 확인할 수 있는데, 각 네트워크에서 사용자의 수가 4명보다 많아지면 기회적 간섭정렬 기법이 신호 최대화 기법보다 높은 성능은 보인다.

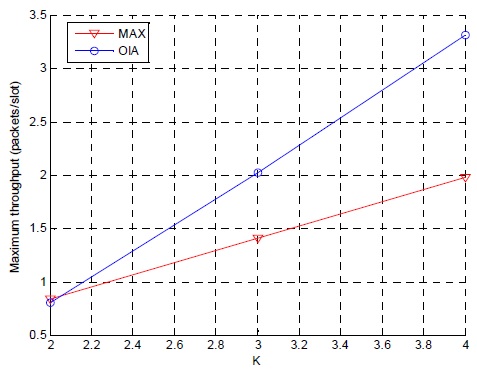
그림 4는 사용자의 안테나의 개수, 액세스 포인트의 안테나 개수, 신호 공간을 모두 셀의 수와 같게 변화 시켰을 때 (즉, K = M =L =S) 두 기술의 최대 전송률 경향을 보여준다.

그림에서 보는 바와 같이 네트워크가 두 개 있을 때만 신호 최대화 기법의 최대 전송률이 미세하게 높다. 3개 이상의 랜덤 액세스 네트워크들이 겹쳐 간섭이 매우 극심한 환경에서는 랜덤액세스 네트워크의 수가 증가할수록 기회적 간섭정렬 기법의 성능이 훨씬 좋음을 알 수 있다.

본 논문은 다수 랜덤 액세스 네트워크가 서로 간섭을 주고받는 네트워크에서 제안된 기회적 간섭정렬 기법과 신호 최대화 기법의 성능을 서로 비교하였다. 신호 대 잡음비, 사용자 수, 셀의 수 변화에 따라 두 기술중 무엇이 더 효과적인지 분석하였고 환경에 따라 두 기법의 성능 사이에 trade-off가 발생한다는 것도 관찰했다.

본 연구에 따르면 간섭이 심하고 사용자의 수가 많을수록 기회적 간섭정렬 기법의 성능이 신호 최대화 기법에 비하여 우수함을 알 수 있다. 그러나 사용자의 수가 적거나 간섭의 양이 크지 않은 상황에서는 신호 최대화 기법이 더욱 좋은 성능을 보임을 관찰하였다. 본 연구를 기반으로 트레이드오프가 일어나는 점을 중점적으로 연구하면 간섭 최소화 기법과 신호 최대화 기법을 결합한 다양한 상황에 따른 최적의 기술을 모색 할 수 있을 것이다.