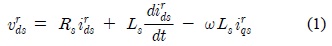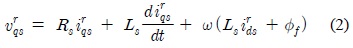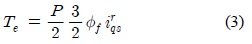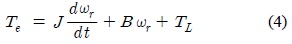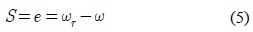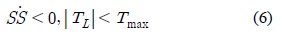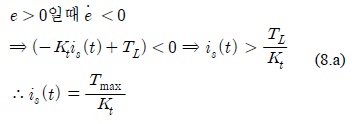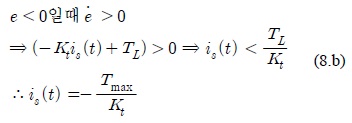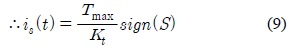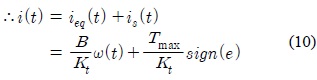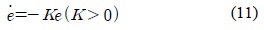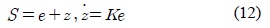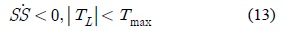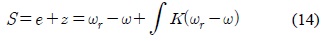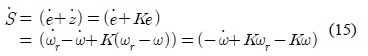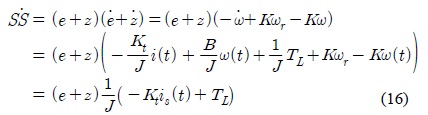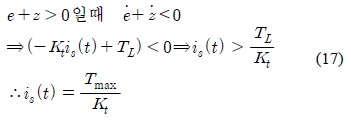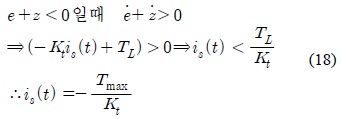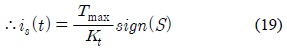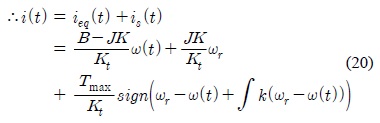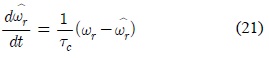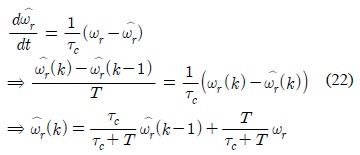Many robust controllers have been studied but most are considered in the theoretical point of view and can be used for only specific systems. So, in this paper, a more practical robust controller is proposed based on SMC(sliding mode control) and disturbance observer. The integral sliding mode is used to eliminate the reaching phase and minimizes the steady-state error, and the disturbance observer reduces the chattering due to the switching input for the bounded disturbances. The inevitable chattering of SMC is also removed by replacing the sign function with dead-zone function. The proposed controller has the improved steady-state error and robustness compared to PID controller.
최근 들어 다양한 산업분야에 적용할 수 있도록 영구 자석 전동기와 전용 드라이버 세트들이 상품화되어 나오고 있다. 이 제품들은 영구자석 전동기 모델에 따라 전용 드라이버를 사용하도록 권장하고 있으며 전동기에 대한 권선저항, 인덕턴스 등의 상세 파라미터는 공개하지 않는다. 이 파라미터들은 전용 드라이버에 내장되어 세트구성을 해야 제대로 사용할 수 있도록 하고 있는 것이다. 이들 전용 드라이버에 내장되어 영구자석 전동기를 제어하는데 쓰이는 제어기는 대부분 PID 제어기가 사용된다. 그 이유는 PID 제어기의 손쉬운 사용법에서 찾을 수 있다. 산업현장에서 어느 정도의 지식을 가지고 PID 제어기 이득을 조정해 봄으로써 사용자가 원하는 응답을 얻을 수 있기 때문이다. 즉 시행착오 기법을 통해서도 소기의 제어 목적을 어느 정도는 달성 할 수 있다. 그러나 PID 제어기는 제어기의 성능이 전동기 파라미터에 좌우된다는 단점을 가지고 있다. 전동기의 상세 파라미터를 공개하지 않는 것도 여기에서 출발한다. 전동기가 운전되고 있는 상황 즉, 환경적 요인, 부하 요건에 따라 전동기 파라미터가 변하게 되어 제어 특성이 달라지는 현상이 발생할 수 있다는 것이다. 이것을 보완하고자 드라이버 제작 업체들은 전동기가 운용되는 상황에 맞도록 PID 제어 이득을 자동 설정할 수 있는 PID 이득 자동설정(auto tuning)기능을 내장하고 있지만 이 기능은 관성 등의 기계적 부하 조건 변화에만 대응할 뿐이며 전동기가 운전 중에 변화하는 파라미터에 대해서는 대처하지 못한다. 이 변화를 통칭하여 시스템의 불확실성이라고 부른다. 이러한 불확실성이 존재함에도 강인하게 제어가 가능하도록 하는 제어 이론의 연구는 많이 진행되어져 왔다. 하지만 이 연구들은 제어 이론의 효용성을 검증하기 위한 실험 수준에 머무르거나 한정적인 특정시스템에만 적용되었고, 범용성을 가지는 상용화된 제품에는 적용되지 못했다.
따라서 본 논문에서는 강인 제어 이론의 실제 전동기제어 시스템 적용에 관한 연구를 수행하였다. 슬라이딩 모드 제어기는 대표적인 강인제어기이지만 정상상태 오차가 발생하고 불연속 입력으로 인한 채터링이 발생하는 단점이 있다[1-3]. 이러한 정상상태 오차를 개선하기 위해 스위칭 함수의 일차 도함수 값이 불연속항 또는 특정 상수로 수렴하도록 하여 도달기간을 미분방정식의 특성을 갖도록 하는 적분 슬라이딩 모드 제어기를 적용하였다[4,5]. 그리고 채터링 현상을 줄이기 위해 외란 관측기를 추가하였다. 외란 관측기를 통해 관측된 외란과 부하를 시스템 입력에 보상함으로써 강인성과 속응성을 유지하면서 슬라이딩 제어 이득을 작게 하여 채터링을 줄일 수 있고, 정상상태 오차도 제거할 수 있었다. 마지막으로 제안한 제어기를 컴퓨터 시뮬레이션을 통해 확인하고 실제 전동기 제어 시스템에 구현하여 제안한 제어기법의 우수성을 검증하였다.
PMSM은 구조상 동기전동기와 동일하며, 고정자는 3상 Y결선이 대칭 분포되어 있고, 회전자는 영구자석으로 이루어져있다. 속도
여기서 는 d축과 q축의 전압과 전류이고,
여기서
슬라이딩 모드 제어입력을 구하기 위하여 슬라이딩 평면을 다음과 같이 설정한다.
여기서 슬라이딩 모드 제어입력
시스템이 안정화할 조건식을 전개하면 아래와 같다.
여기서
위 식을 통해 구한 시스템의 안정화 조건은 다음과 같다.
두 식으로부터 얻은 불연속 제어입력은 다음과 같다.
따라서 등가 제어입력과 불연속 제어입력으로 이루어진 슬라이딩 모드 제어입력은 최종적으로 다음과 같다.
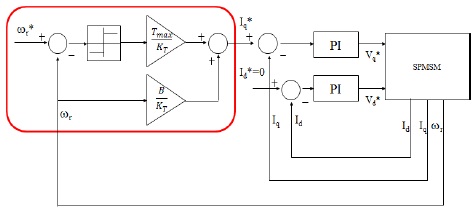
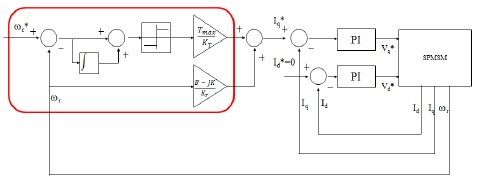
이렇게 구해진 슬라이딩 모드 제어입력을 이용하여 구성한 속도제어기는 그림 1과 같다.
슬라이딩 모드 제어기를 살펴보면 슬라이딩 평면을 기준으로 불연속입력이 매우 큰 이득을 가지고 스위칭을 하는 형태이다. 이로 인해 시스템에 파라미터 불확실성이 존재하여도 그 불확실성에 강인한 특징이 나타난다. 그러나 이 강인함은 시스템의 상태가 슬라이딩 평면상에 있을 때에 한정된다. 시스템의 상태가 슬라이딩 평면상에 있지 않고 슬라이딩 평면에 다가가고 있는 상태인 도달모드(reaching mode)에서 외란에 영향을 받을 수 있는 단점이 있다[1,2]. 따라서 이러한 단점을 보완하고자 적분 슬라이딩 모드 제어기를 채택한다.
도달모드를 제거하기 위해 슬라이딩 평면에 다음과 같은 동특성을 부여한다.
적분 슬라이딩 모드 제어입력을 구하기 위하여 아래와 같이 슬라이딩 평면을 설정한다.
여기서 슬라이딩 모드 제어입력과 마찬가지로 적분 슬라이딩 모드 제어입력
이 슬라이딩 평면을 사용하여 시스템이 안정화할 조건은 아래식과 같다.
시스템이 안정화할 조건식을 전개하면 아래와 같다.
여기서
식(16)을 통해 구한 시스템의 안정화 조건은 다음과 같다.
두 식으로부터 얻은 불연속 제어입력은 다음과 같다.
따라서 등가 제어입력과 불연속 제어입력으로 이루어진 슬라이딩 모드 제어입력은 최종적으로 다음과 같다.
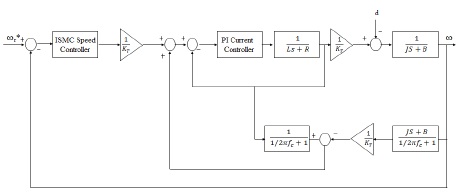
이렇게 구해진 적분 슬라이딩 모드 제어입력을 이용하여 구성한 속도제어기는 그림 2와 같다. 슬라이딩 평면이 적분 형태로 구성되어 있어 도달모드가 제거되었다. 슬라이딩 평면에 동특성이 부여되어 슬라이딩 모드 제어기가 가지는 단점이 보완되었음을 알 수 있다[4,6]. 하지만 불연속입력이 여전히 존재하고 이로 인해 발생하는 채터링은 전동기 제어시스템을 불안정하게 할 수도 있고 부가적으로 소음, 진동, 열의 발생과 기계적 연결계통의 마모 등을 유발하여 시스템의 수명을 단축시킬 수 있다[1]. 따라서 채터링의 원인인 불연속 제어입력의 큰 이득을 줄임과 동시에 불확실성에 강인함을 유지하기 위해 외란관측기를 도입하였다.
외란 관측기는 전동기 제어 시스템에 인가되는 외란들을 제거하여 실제 시스템을 설계한 공칭모델처럼 동작하게 하는 특징이 있어 강인 제어 및 외란 제거 제어의 여러 분야에 널리 적용되고 있다[6-9]. 저역 통과 필터인 Q-필터를 사용함으로써 불안정했던 시스템의 역모델이 안정화되고 고주파 성분인 잡음을 차단할 수 있으며, 저주파 형태를 가지는 외란만을 통과시켜 외란을 검출할 수 있게 된다[10,11].
논문에서는 고급제어기의 범용 전동기 드라이버 적용을 목적으로 하고 있기 때문에 전동기 제어 시스템에 인가되는 외란 제거에 우수한 성능을 보여주면서도 마이크로프로세서의 연산 부담을 줄일 수 있는 외란관측 기가 필요하다. 이러한 조건을 만족하는 외란 관측기를 구현하기 위해서 설계하기 간단하고 구현하기 쉬운 차저역 통과 필터를 사용하여 Q-필터를 설계하였다.
여기서 —필터출력,
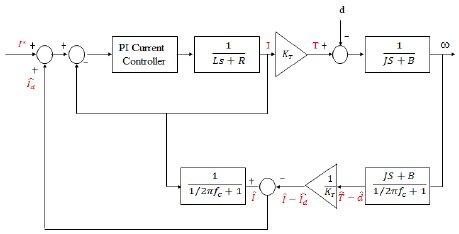
그림 4는 1차 저역 통과 필터를 이용한 전동기 제어시스템의 외란관측기를 나타내었다.
그림 4에 표현된 외란관측기는 연속 시간 영역에서 전달함수로 나타낸 것이다. 하지만 외란관측기를 마이크로프로세서에서 구현하려면 이산 시간 방정식의 형태로 변환하여야 한다. 먼저 1차 저역 통과 필터를 이산방정식으로 변환하면 아래와 같다.
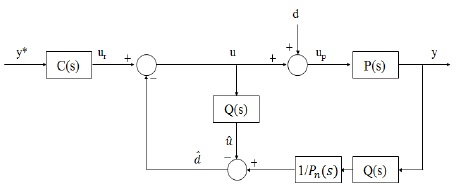
그림 5는 본 논문에서 제안한 강인 제어기를 구성한 블록도이다. 그림에서 보는 바와 같이 2-루프(loop) 구조를 가지고 있다.
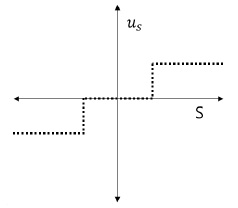
첫 번째 루프는 내부루프(internal-loop)로서 외란을 관측하여 전향 보상함으로써 외란의 영향을 가능한 상쇄시켜 실제 시스템을 설계한 공칭모델처럼 동작하게 하는 외란관측기로 구성되어 있고, 두 번째 루프는 외부 루프로서 시스템을 원하는 성능 기준에 만족하게 동작시키기 위한 적분 슬라이딩 모드 제어기로 구성되어 있다. 외란 관측기에 의해 외란이 제거되면 슬라이딩 모드 제어기의 불연속 제어입력 크기를 줄일 수 있다. 불연속 제어입력의 크기를 줄이면 채터링은 감소하지만 완전히 제거되지는 않는다. 채터링이 완전히 제거되기 위해서는 불연속 제어입력이 사라져야하지만 슬라이딩 모드 제어기의 강인성은 불연속 제어입력에 의해 나타나는 특성이므로 불연속 제어입력을 없애는 것은 불가능하다. 이러한 문제는 불연속 제어입력이 구간에 따라 변하는 가변이득을 채택함으로써 해결이 가능하며 프로그램으로 구현이 비교적 간단한 그림 6의 데드존 함수를 사용하였다.
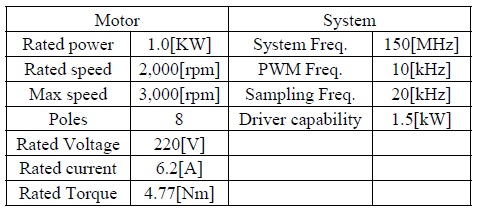
본 논문에 제안한 제어기를 검증하고자 모의시험 및 실험을 수행하였다. 본 실험에 사용된 전동기의 사양과 제어 시스템 사양은 표 1과 같다.
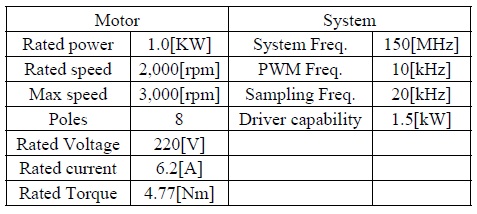
영구자석 전동기 및 제어 시스템 사양
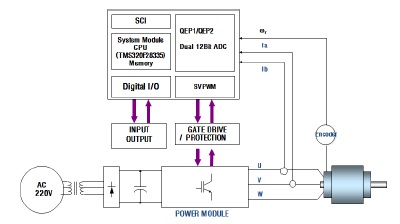
그림 7은 본 논문에서 제안한 제어기의 적용을 위해 개발된 전동기 제어 시스템의 블록도이다. 전동기 제어 시스템은 전동기 시험장치, 전기 부하장치, 전동기 드라이버와 알고리즘 구현을 위해 고속 연산 및 부동소수점 연산이 가능한 DSP(TI사 TMS320F 28335)가 탑재된 주 제어기로 구성된다. 그림 8은 실험을 진행하기 위해 구성된 전동기 시험 장치이다. 실험에 사용되는 1kW SPMSM을 토크센서를 통해 3kW 부하전동기에 연결하고 토크 인디케이터에서 토크를 측정한다.
모의시험은 5초간 수행되며, 0.5초부터 0.2초간 300[rpm]까지 가속시키고 2.5초에 step부하를 인가한다.
그림 9는 PI 속도 제어기의 모의실험 결과이다. 부하(3.92[Nm])가 인가 된 후 정상상태 복귀까지 상당히 느린 응답을 나타내고 있어 외란에 영향을 많이 받는 것을 알 수 있다. 즉 PI 제어기는 파라미터 불확실성에 대해 강인하지 못함을 알 수 있다.
그림 10~12는 SMC 속도 제어기의 모의실험 결과이다. PI 속도 제어기에 비해 속도 응답성이 좋아졌고 외란에 영향을 받지 않음을 그림 10에서 확인할 수 있다. 하지만 부하가 인가 된 후 속도를 확대한 그림 11에서 작은 부하(0.49[Nm])가 인가 됐음에도 불구하고 정상상태 오차가 발생하는 것을 확인할 수 있다. 뿐만 아니라 그림 11,12에서 채터링이 발생하는 것을 확인할 수 있다.
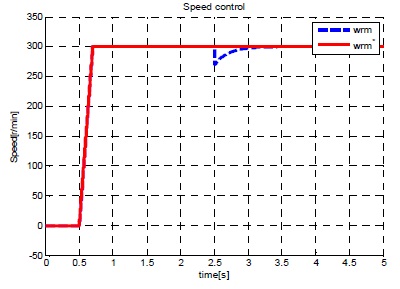
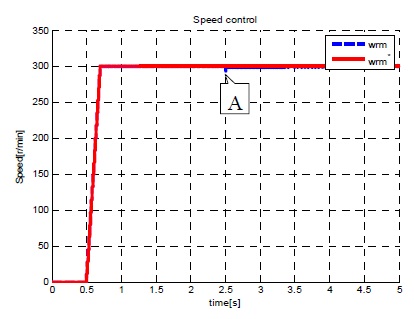
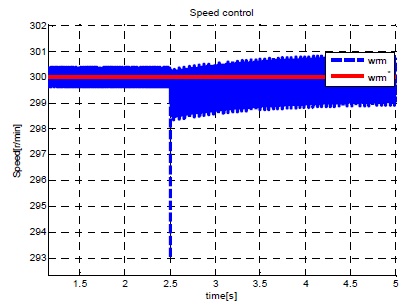
그림 13~15는 SMC 속도 제어기가 가지는 문제점 중 정상상태 오차를 개선하기 위해 채택된 ISMC 속도 제어기의 시뮬레이션 결과이다. 그림 14는 부하가 인가된 후 속도를 확대한 그래프로써 채터링은 여전히 발생되고 있으나 매우 큰 부하(3.92[Nm])가 인가된 후에도 정상상태 오차가 발생하지 않아 SMC 제어기에 비해 정상상태 오차가 개선되었음을 확인할 수 있다.
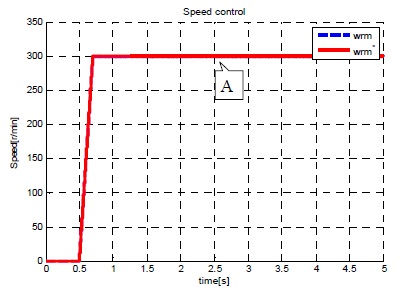
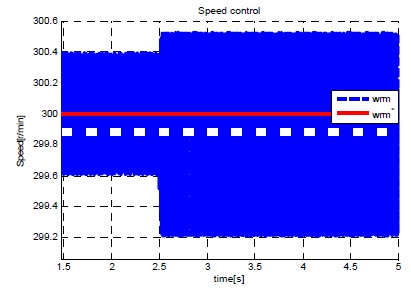
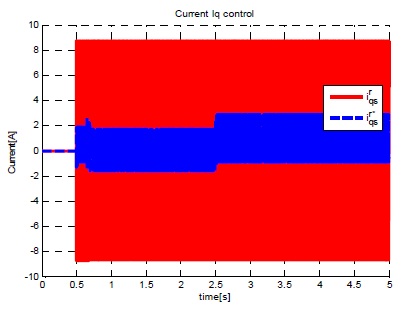
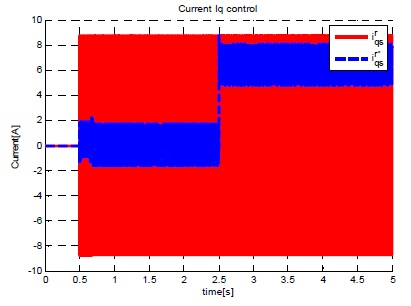
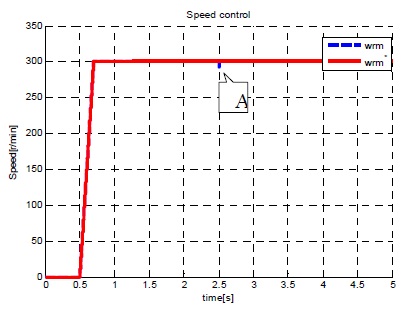
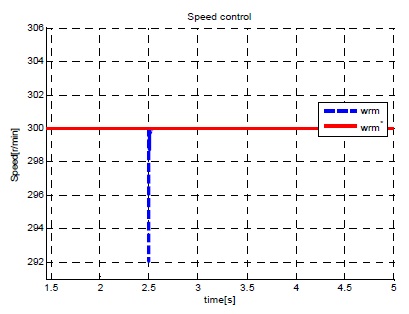
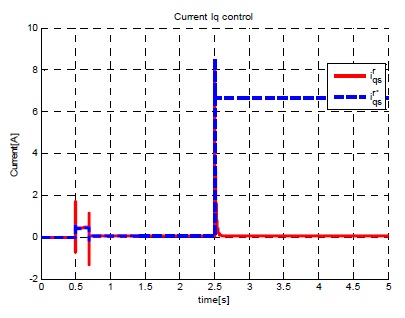
그림 16~18은 ISMC 제어기에 여전히 존재하는 채터링을 개선하기 위해 ISMC 속도 제어기에 외란관측기를 적용한 시뮬레이션 결과이다.
매우 큰 부하(3.92Nm)가 인가 된 후에도 빠른 속도 응답을 보이고 정상 상태 오차가 발생하지 않는 것을 그림 17에서 확인할 수 있다. 그림 17,18에서 보는 것과 같이 ISMC속도제어기에 외란관측기를 추가함으로써 속도, 전류 채터링이 사라졌음을 확인할 수 있다.
본 실험에서는 PI제어, 슬라이딩 모드 제어, 적분슬라이딩 모드 제어, DOB-적분 슬라이딩 모드 제어 각각에 대해 속도 지령에 따른 응답특성과 외란 발생 시에 속도 제어 성능 비교 등의 실험으로 제안한 제어기의 타당성을 검증하였다.
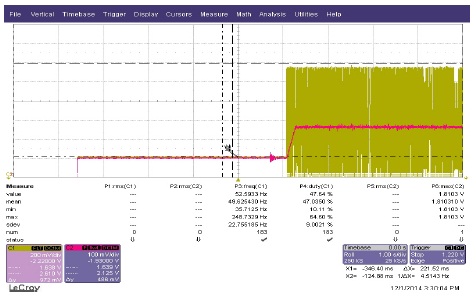
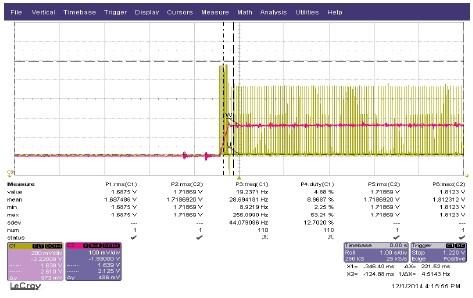
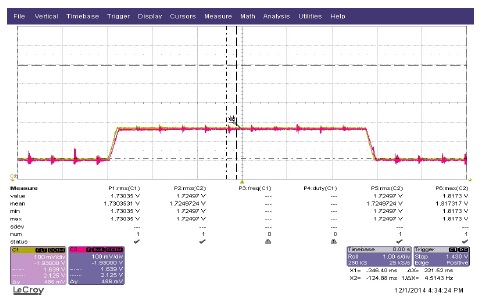
그림 19는 PI 속도 제어기를 이용한 실험 결과이다. 그림 19는 부하 변동(2.16[Nm]→3.92[Nm]→2.16[Nm])에 따른 속도의 응답을 나타낸 것으로 부하 변동에 따라 느린 응답을 나타내고 있어 외란에 영향을 많이 받는 것을 알 수 있다. 즉 시뮬레이션에서 확인한 바와 같이 PI 제어기는 파라미터 불확실성에 대해 강인하지 못하다는 것 실험을 통해서도 확인하였다.
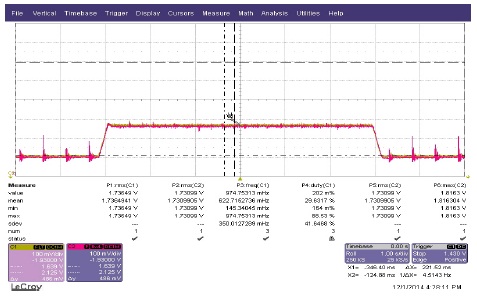
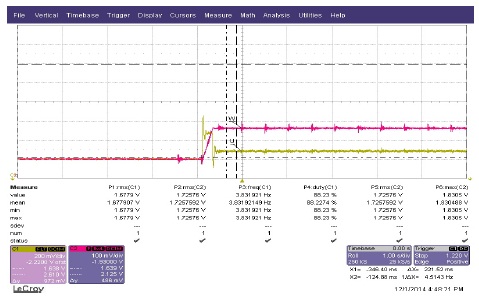
그림 20,21은 PI제어기의 느린 응답성과 파라미터 불확실성에 강인하지 못한 문제점을 개선하고자 채택된 SMC 속도 제어기를 이용한 실험 결과이다. PI 속도 제어기에 비해 속도 응답성이 좋아졌고 외란에 영향을 받지 않음을 확인할 수 있다. 하지만 정상상태 오차가 발생하고 있으며, 속도와 전류에 채터링이 발생하는 것을 확인할 수 있다.
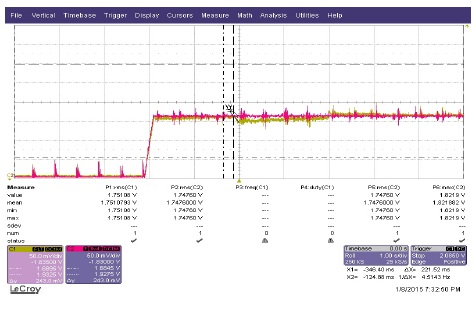
그림 22,23은 SMC 속도 제어기가 가지는 문제점 중 하나인 정상상태 오차를 개선하기 위해 채택된 ISMC 속도 제어기를 이용한 실험 결과이다. 그림 22에서 확인 할 수 있듯이 SMC 제어기와 유사하게 아주 빠른 속도 응답을 보이고 있으며 SMC 제어기에 비해 정상상태 오차가 개선되었음을 확인할 수 있다. 그림 22,23에서는 SMC 속도 제어기와 동일하게 여전히 속도와 전류에 채터링이 발생하지만 SMC 속도 제어기보다는 적은 채터링이 발생하는 것을 확인할 수 있다.
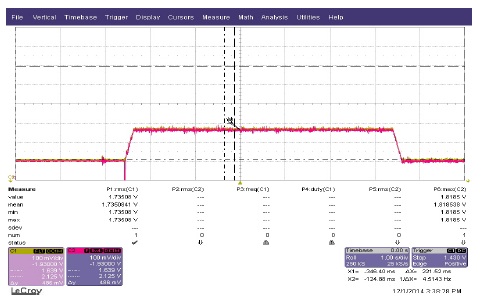
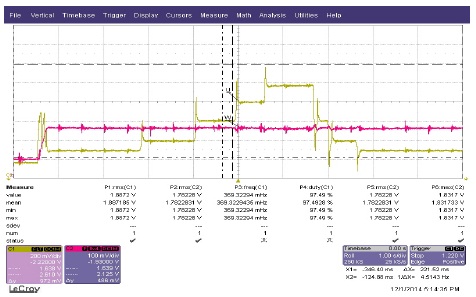
그림 24~26은 ISMC 제어기에 여전히 존재하는 채터링을 개선하기 위해 ISMC 속도 제어기에 외란관측기(DOB)를 추가한 실험 결과이다. 그림 24,25에서 확인 할 수 있듯이 기존 ISMC 속도 제어기의 속도 응답특성을 그대로 유지하고 있다. 또한 ISMC속도제어기에 외란관측기를 추가함으로써 속도, 전류 채터링이 사라졌음을 확인할 수 있다. 그림 26은 부하 변동(0.196[Nm]→0.686[Nm]→1.96[Nm]→2.94[Nm]→3.92[Nm])에 따른 속도와 Iq 전류를 나타낸 것이다. 빈번한 부하 변동에도 정상 상태 오차 없이 빠른 속도 응답을 보이고 있으며 부하 변동에 영향을 받지 않고 있어 파라미터 불확실성에 대해 강인하다는 것을 확인 할 수 있다.
본 논문에서는 일반적인 전동기 제어시스템이 지니는 불확실성을 극복하고자 슬라이딩 모드 제어기를 도입하고, 슬라이딩 모드 제어기에서 발생하는 정상상태 오차를 개선하고자 적분 슬라이딩 모드 제어기를 범용 전동기 제어 드라이버에 구현하였다. 그리고 슬라이딩 모드 제어기 고유의 채터링 문제를 개선하기 위해 외란 관측기를 추가로 구현함으로써 부하변동에 따른 빠른 부하 관측이 가능하여 응답성이 향상되었고 불연속 제어입력 이득의 크기를 줄이고 가변이득을 적용함으로써 채터링(chattering)을 제거할 수 있었다.
각 단계별로 문제점을 도출하고 그 문제점을 개선하기 위한 과정에서 Back-stepping 기법을 이용하였으면 Matllab simulink 컴퓨터 시뮬레이션과 실제 전동기 제어 시스템에 구현을 통해 설계된 제어기의 타당성을 검증하였다.
따라서 본 논문에서는 특정분야에 특정한 용도로만 적용되던 고급 제어기를 범용 전동기 드라이버에 적용 할 수 있도록 구현함으로써 사용자의 개별적인 파라미터 설정없이 정격 운전영역에서 신뢰성과 안정성을 확보할 수 있는 범용화된 고급제어기를 개발하고 검증하였다.