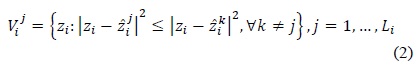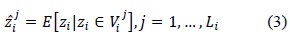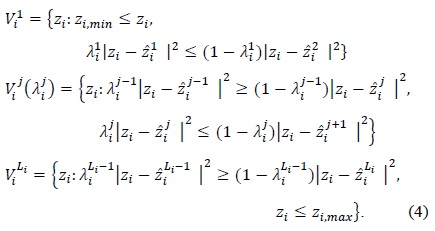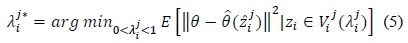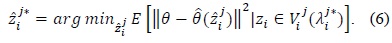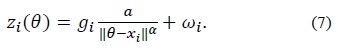In distributed estimation systems where many sensor nodes located at different sites operate on power-limited batteries, each node monitors its environmental conditions, such as temperature, pressure, or sound, related to the parameter of interest and sends the data to a fusion node, which then estimates the parameter value. In such powerconstrained systems, the quantization of sensing data has been an attractive topic of research for signal processing researchers since efficient quantization at each node has a significant impact on the rate-distortion performance of the system.
For a source localization system where each sensor measures the signal energy, quantizes it, and sends the quantized sensor reading to a fusion node where the localization is performed, the maximum likelihood (ML) estimation problem using quantized data was addressed and the Cramer–Rao bound (CRB) was derived for comparison [1], assuming that each sensor used identical (uniform) quantizers. However, if the node locations are known prior to the quantization process, sensor nodes can exploit the correlation between their measurements to design quantizers minimizing the system-wide metric (i.e., the estimation error) to replace typical quantizers, which would be devised to minimize the local metric, such as the reconstruction error. It has been demonstrated that a significant performance gain can be achieved by using such quantizers with respect to simple uniform quantization at all nodes.
There is a difficulty in designing independently and locally operating quantizers that minimize a global metric (e.g., the estimation error is a function of measurements from all nodes). To circumvent this, a
Previously, we proposed iterative quantizer design algorithms in the Lloyd algorithm framework (see also [7-9]), which design independently operating quantizers by reducing the estimation error at each iteration. Since the Lloyd algorithm is focused on minimizing a local metric (e.g., reconstruction error of local sensor readings) during quantizer design, some modification would be inevitable in order to achieve convergence with the global metric in the Lloyd design. Hence, we suggested a weighted sum of both the metrics as a cost function (i.e., local +
In this paper, we propose an iterative design algorithm in the generalized Lloyd framework that seeks to design independently operating scalar quantizers by partitioning quantization regions based on the weighted distance rule so as to minimize the estimation error. We search for the weights corresponding to the codewords such that the weighted partition of the regions using the codewords will result in an iterative reduction in the system-wide performance metric. To avoid a high computational complexity, we suggest a sequential search for the weights without causing performance degradation. We show that convergence of the proposed algorithm is guaranteed by reducing the global metric in each iteration and applying our design algorithm to a source localization system where the acoustic amplitude sensor model proposed in [11] is considered. We demonstrate through experiments that improved performance over traditional quantizer designs can be achieved by using our design technique. We also evaluate the proposed algorithm by a comparison with recently published novel design techniques [9,10], both of which were recently developed for source localization in acoustic sensor networks, the application considered in this work. As expected, the
The rest of this paper is organized as follows: we present the problem formulation for quantizer design in distributed estimation in Section II. We then consider quantization based on weighted distance and elaborate the proposed design process in the Lloyd algorithm framework in Section III. As an application system, we consider source localization in acoustic sensor networks in Section IV and then, evaluate the proposed technique for this system in Section V. Finally, we present the conclusions and future directions for research on distributed systems in Section VI.
In distributed estimation systems, it is assumed that
where
III. QUANTIZATION BASED ON WEIGHTED DISTANCE
Standard quantization follows the minimum distance rule on which the next quantization partition is conducted as well as the codeword computation in an iterative manner. Formally, the Voronoi region construction (i.e., quantization partitions) is defined as follows:
where
Clearly, the two main steps defined as Eqs. (2) and (3) in the typical Lloyd design minimize the average reconstruction error
It is noted that the minimum distance rule is generated with = ½, which will create the standard construction defined in Eq. (2). Our weighted distance rule considers various cases of partitioning determined by the weights 0 < < 1. This will produce a set of candidate partitions for our design process.
Second, we search for the optimal weight starting with that minimizes the estimation error over the corresponding quantization partition:
where () , the abbreviated notation for , can be computed by replacing with for all
Once the optimal weights are obtained, the next step would be to update the codewords over the Voronoi regions determined by their corresponding optimal weights: formally,
Note that the construction of the Voronoi regions, the search for optimal weights, and the subsequent computation of the codewords given in Eqs. (4), (5), and (6), respectively, are repeated at each sensor node until a certain criterion is satisfied. Clearly, these procedures are guaranteed to reduce the estimation error in each iteration, leading to convergence of the design algorithm.
>
A. Summary of Proposed Algorithm
Given
Algorithm 1: Iterative quantizer design algorithm at sensor
Step 1: Initialize the quantizers with and ,
Step 2: For each , construct the partitions ,
Step 3: Given a set of optimal weights {}, update the codewords ,
Step 4: Compute the average distortion D=
Step 5: If (D
Step 6: Replace by
Note that the quantizers are designed offline by using a training set that is generated on the basis of Eq. (1) and the parameter distribution
IV. APPLICATION OF QUANTIZER DESIGN ALGORITHM
We apply our design algorithm to a source localization system where sensor nodes equipped with acoustic amplitude sensors measure source signal energy, quantize it, and transmit the quantized data to a fusion node for estimation. For collecting the signal energy readings, we use an energy decay model proposed in [11], which was verified by a field experiment and was also used in [15,16]. This model is based on the fact that the acoustic energy emitted omnidirectionally from a sound source will attenuate at a rate that is inversely proportional to the square of the distance in free space [17]. When an acoustic sensor is employed at each node, the signal energy measured at node
Note that θ indicates the source location to be estimated and the sensor model
In this section, we discuss a weighted distance-based quantizer (WDQ), the quantizer designed using the algorithm proposed in Section III-A. In designing WDQ, we use the equally distance-divided quantizer (EDQ) to initialize quantizers (see Step 1 in Section III-A) because EDQ can be used as an efficient initialization for quantizer design due to its good localization performance in acoustic amplitude sensor networks [8, 9]. We generate a training set from the uniform distribution of source locations and the model parameters in Eq. (7) set as
>
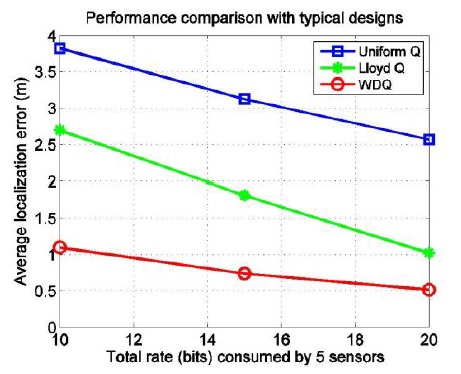
A. Performance Comparison with Typical Designs
In this experiment, 100 different five-node configurations are generated in a sensor field measuring 10 × 10 ㎡. A test set of 1000 random source locations is generated for each configuration to collect signal energy measurements with
>
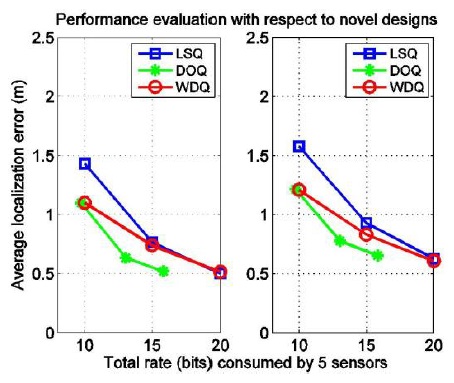
B. Performance Evaluation: Comparison with Previous Novel Designs
In this experiment, we evaluate the proposed algorithm by comparing it with the previous novel designs, such as distributed optimized quantizers (DOQs) in [10] and the localization-specific quantizer (LSQ) in [9] since both of them are optimized for distributed source localization and can be viewed as DSC techniques, which are developed as a tool to reduce the rate required to transmit data from all nodes to the sink. These design techniques are applied for 100 five-sensor configurations by using the EDQ initialization with
>
C. Sensitivity Analysis of Design Algorithms
In this section, we first investigate how the performance of the proposed design algorithm can be affected by the perturbation of the model parameters with respect to the assumptions made during the quantizer design phase. We further examine the design algorithms to understand how sensitive the localization results will be with respect to the presence of the measurement noise.
1) Sensitivity of WDQ to Parameter Perturbation
We design WDQ with
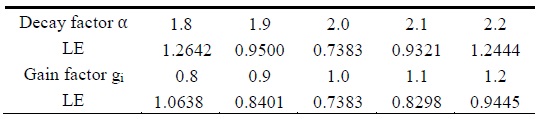
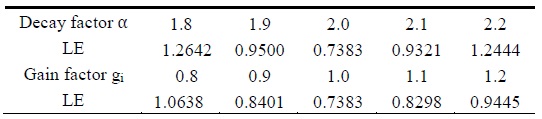
Localization error (LE) of weighted distance-based quantizer (WDQ) with Ri = 3 due to variations of the model parameters
2) Sensitivity of Design Algorithms to Noise Level
We design quantizers with
In this paper, we proposed an iterative quantizer design algorithm optimized for distributed estimation. Since the goal was to design independently operating quantizers that minimized the global metric such as the estimation error, we suggested a weighted distance rule that allowed us to partition quantization regions so as to reduce the metric iteratively in the generalized Lloyd algorithm framework. We showed that the system-wide metric could be minimized for quantizer design by searching the optimal weights in a sequential manner, yielding a substantial reduction in computational complexity. The proposed algorithm was shown to perform quite well in comparison with typical standard designs and previous novel ones. Furthermore, we demonstrated that the proposed quantizer operated robustly to mismatches of the sensor model parameters. In the future, we will continue to work on novel quantizer design methodologies and their theoretical analysis for distributed systems.