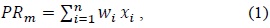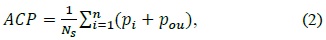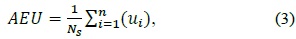Mobile communication has won the race in the field of communication in the 21st century. The proliferation of mobile devices (e.g., laptops, PDAs, and mobile phones) coupled with wireless communication technologies such as Bluetooth, Wi-Fi, and near-field communication (NFC) strongly motivates mobile applications for on-the-fly information sharing. Although mobile applications are built on top of various mobile platforms (e.g., iOS, Android, Windows CE, and Blackberry), most of them rely on the basic form of data, i.e., phone call (PC), short message (SMS), multimedia message (MMS), and Internet data (D). Moreover, service providers interact with the mobile devices through these data media for providing communication services, while mobile users pay for them.

These combination of services have various data prices, which are defined on the basis of the usage of PC, SMS, MMS, D, or their combinations. Interestingly, these data prices are also varied according to services and their respective usages across mobile users. Our work focuses on how to dynamically and efficiently define such data prices for individual or combined communication services in the field of mobile communication so that mobile users can obtain optimal services for the cost of data that they incur and service providers can ensure the quality of services (QoS) with justified data prices. Essentially, we propose a mobile service-based pricing platform, denoted as MobPrice, to provide various dynamic data-pricing schemes in the field of mobile communication. Here, for the sake of conciseness, we represent all communication services (i.e., PC, D, SMS, and MMS) and their combinations as mobile services (MSs). Moreover, providers and consumers of MSs are represented as mobile service providers (MSPs) and mobile users (MUs), respectively, throughout this paper.

Observe that the goal of dynamic data pricing is to create a “win-win” situation for both service providers and their consumers, with a reduction in the network congestion cost and with effective data usage schemes for MUs [1]. The interest of service providers is to motivate users to adopt their simple, preferably flat-rate, pricing for high QoS to operate the network at its optimal level. MobPrice has the aligned goal of effective sharing of communication services through data-usage sharing, while reducing the overall communication cost.

In real-world scenarios, cost-effective data usage and sharing of data with others are the core objectives for MUs. Because of high-traffic applications such as audio/video sharing and streaming apps on tiny mobile devices, MUs may run out of the available/allowed data usage within a certain time frame. In contrast, text-sharing applications (e.g., social networking, messaging, and e-mail) may have under-utilization of the available data usage. Thus, the sharing of such data usage balances the users’ needs at low costs.

Let us consider that Alice and Bob have subscribed to an Internet data plan of 5 GB and 2 GB, respectively, with onemonth validity. If Alice has utilized only 3 GB of data, while Bob runs out of data usage well before the expiry of his plan, then Alice may share data with Bob at a lower rate than the original rate charged by the service provider, as the remaining 2 GB of data is of no use after its expiry. Such collaboration among users brings high utilization of data usage at a low cost.

Moreover, this collaboration inspires “offshore business,” where an MU acts as a relay peer, who subscribes to the plan and further distributes it among other MUs. This essentially creates a win-win situation for both (MUs and MSPs); i.e., MUs get the benefit of reduced-cost MSs because of service distribution, and MSPs get the benefit of a higher number of subscriptions.

The main contributions of our work are three-fold:

Interestingly, our performance study demonstrates that the pDP is indeed effective as compared to kDP because of the effective sharing of MSs, thereby reducing the communication cost per user. In contrast, cDP outperforms both kDP and pDP as cDP incorporates the benefits of both the schemes, i.e., kDP’s scaled-price approach and pDP’s peersharing-price approach.

The remainder of this paper is organized as follows: Section II presents the related work. The architecture of MobPrice is proposed in Section III. Sections IV, V, and VI describe the kDP, pDP, and cDP schemes, respectively, for the data pricing of various mobile services along with their respective theoretical description. Our performance study is presented in Section VII. Finally, Section VIII concludes MobPrice.

This section discusses the various existing data-pricing schemes and approaches proposed for mobile communication.

The communication technologies, starting from telegraph and telephone to the latest e-mail and the Internet, follow the same typical methodology in terms of their services and usage. The analysis in [2] shows a relationship between pricing and the quality of the given services. Furthermore, it presents a method to increase the overall revenue by increasing the service usage across the users, thereby resulting in higher social welfare.

The work in [3] represents a study on multiple service class networks to allow network resources to be focused on performance-sensitive applications. Here, pricing policies help to spread benefits of multiclass services among users. While the incentivization of MUs leads to optimal network performance because of the self-interest of the users.

In the communication world, a conventional data plan enables users to use only a single device per data plan, while a shared data plan allows users to share data among multiple users and devices. The analytical comparison of singledevice vs. shared data plans along with their benefits and limitations is presented in [4]. The work shows that a shared data plan is more profitable than a single-device data plan as multiple devices have a diverse need of services; hence, services subscribed under the same plan can be distributed across multiple devices, thereby reducing the overall cost. This work is aligned with MobPrice, but it does not consider the level of services as well as the users’ group-based sharing across the mobile network.

Nowadays, ISPs use pricing as a network congestion control tool because of the increasing demand of broadband data. In the US and Europe, most of the operators follow a usage-based pricing model instead of a flat-rate pricing model for providing either wired or wireless services. However, there are certain limitations (e.g., management overhead and time coordination) of the usage-based pricing model. In order to overcome such limitations, [5] proposes a time-based incentive scheme to reduce network congestion. Time-dependent pricing categorizes incentives into static and dynamic categories and allows users to time-shift their data demand from peak to off-peak hours. Incentivizing users for their time-shifting of data results in effective network traffic management. However, this work does not consider usage sharing among multiple users in a network.

In a similar vein, [6] presents a survey of various pricing schemes, which includes a flat-rate scheme, a usage-based scheme, and a combination of both called the cap scheme. Implementation of a usage-based scheme enables the ISP to obtain a relatively high profit and enables effective traffic management as compared to a flat-rate scheme. In contrast, the cap scheme facilitates the ISP to increase its overall revenue. Furthermore, [7] proposes a time-dependent pricing system for mobile data, denoted as TUBE, which considers the time and amount of data consumption in order to facilitate users to choose their time and volume of usage. TUBE performs three tasks: calculates the prices of peak hours for the ISP in order to control congestion; offers lower prices to MUs for less congested hours; and enables MUs to provide system feedback.

Spatio-temporal variations of MUs sometimes cause network congestion during peak hours or at a hotspot. [8] presents a time- and location-aware pricing scheme, where users are incentivized on the basis of their efforts for flattening the network traffic. The users, who have scheduled their mobile traffic according to the time and location announced by the provider, are eligible to receive the incentives. This scheme creates a “win-win” situation for both the operator and a user.

Each user in a network transmits data as per the nominal rates of contract. Here, the transmission rate of limited data is lower than the contracted rates; however, the user may sustain any rate for the transmission of unlimited data because data are the first priority for the user. The pricing scheme proposed in [9] works effectively by using unutilized resources of limited transmission by allocating them to over-utilized users. However, a service provider has to decide only one price for all users. This work differs from MobPrice as the data-sharing prices are decided by the users but not by the service provider.

The survey in [10] discusses pricing schemes along with the affected elements of the networking environment and the characteristics of mobile subscribers and service providers with the core focus on static pricing vs. dynamic pricing. The further categorization of these schemes is defined on the basis of various affecting factors, such as subscription type, negotiation capabilities, network capacity, bandwidth and frequency spectrum, network hops, and base stations.

[11] presents an overall study of various pricing schemes for broadband multiservice networks. By considering a number of criteria, such as network, economy, social efficiency, and suitability for congestion control, an overview of flat pricing, priority pricing, Paris-Metro pricing, smart-market pricing, responsive pricing, expected capacity pricing, edge pricing, and effective bandwidth pricing is to be studied. Moreover, [12] presents a framework for dynamic resource allocation by considering an online traffic estimator. This framework helps the provider to effectively maximize profit, which is demonstrated through a performance study.

The optimization model, called the differentiated services framework (DiffServ) [13], offers multiple QoS over IP networks. Moreover, priority pricing-based optimal network resource allocation (PBORA) considers bandwidth allocation for different service quality levels to maintain efficiency.

MobPrice consists of three entities, namely mobile users (MUs), mobile service providers (MSPs) and mobile services (MSs). Here, MS is in one of the four following forms of data: phone call (PC), Internet data (D), short message (SMS), and multimedia message (MMS). Each MSP provides MSs to the MUs in mobile networks, while charging MUs for these MSs subject to various communication factors such as mobile usage, users’ privileges, and time-specific requirements. Furthermore, the MSP designs various payment plans (P), which are defined as the combined charges to multiple MSs with a limited validity period. For example, a monthly $50 payment plan can be used for 100 PCs, and includes 2 GB of D, 5000 SMS, and 100 MMS. MUs subscribe to these payment plans (also called plans) offered by the MSP.

In MobPrice, an MU performs the following tasks: 1) subscribes to plans for mobile communication, 2) requests special MSs for extra usage according to its need and privileges, and 3) collaborates with other MUs towards the selection of an optimal plan for MSs provided by the MSP. On the other hand, the MSP is responsible for 1) designing various plans, offered as subscriptions to MUs; 2) updating plans over a period of time, based on MUs’ requests and their data usages; and 3) suggesting an optimal plan to MUs.

Furthermore, MSs are provided in the form of either individual services of PC, D, SMS, or MMS or their various combinations. Each MS in MobPrice is a unique entity, which is defined on the basis of data usage and data pricing. For example, a plan with only 100 PCs is different from a plan with 1 GB of D. Moreover, data prices may vary across plans even though their MS usages are the same or less in quantity. For example, plan p1 costs $30 for 1 GB of D with 100 MMSs, while plan p2 costs $40 for 2 GB of D with 100 PCs. Observe that the MSP has defined these plans according to MU usages.

Further, the MSP targets to maximize the revenue by providing effective payment plans for their MSs to the MUs, thereby increasing the overall data usage as well as reducing data prices to create a “win-win” situation among MSPs and MUs.

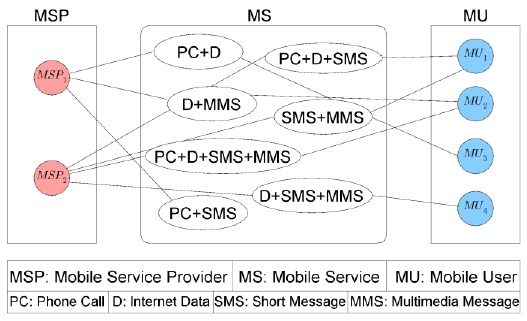
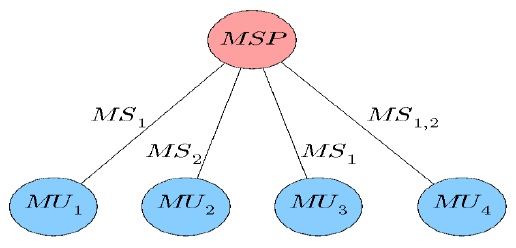
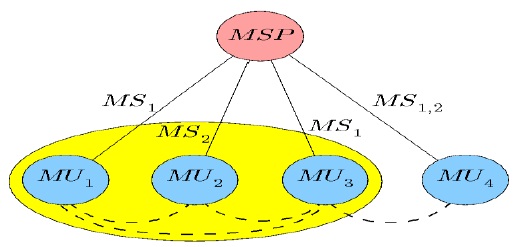
Fig. 1 illustrates the architecture of MobPrice. Here, MSP₁ and MSP₂ represent mobile service providers that offer various MSs. These MSs are made up a combination of PC, D, SMS, and MMS. As shown in Fig. 1, few MSs have PC and D, some others have SMS and MMS, and the rest have full service as they consist of all data forms. Furthermore, each MS connects an MU to the MSP. Notably, an MU can subscribe for one or more mobile services; e.g., MU₁ subscribes to two services, which consist of PC, D, and SMS; and SMS and MMS. Both of them are provided by MSP₂. On the other hand, MSs subscribed by MU₂ are provided by MSP₁ (i.e., service consists of D + MMS) and MSP₂ (i.e., service consists of PC + D + SMS + MMS). Observe that the MSP charges for each of the MSs defined; thus, all these MSs form various payment plans related to mobile communication in MobPrice.

Now, let us understand how data pricing has been considered in MobPrice. Here, we consider all data prices in the US dollars ($). Each MS is defined on the basis of the individual usages of data forms. Hence, the total price p_MS of an MS is evaluated as p_MS = p_PC + p_D + p_SMS + p_MMS, where p_PC, p_PD, p_SMS, and p_MMS denote the total offered usage prices for PC, D, SMS, and MMS, respectively. For example, let us consider that a given plan p allowing 100 PCs (i.e., 100 minutes of phone calls) costs $10, that allowing 1 GB of D costs $25, that allowing 1000 SMSs costs $20, and that allowing 100 MMSs costs $5. Therefore, the total price p_MS for p is $60 (=$10 + $25 + $20 + $5).

Observe that the above example is a flat-rate usage-based data-pricing scheme, where the overall cost of the plan is the summation of the individual service charges based on the usage. Now, let us discuss the various data-pricing schemes for mobile communication.

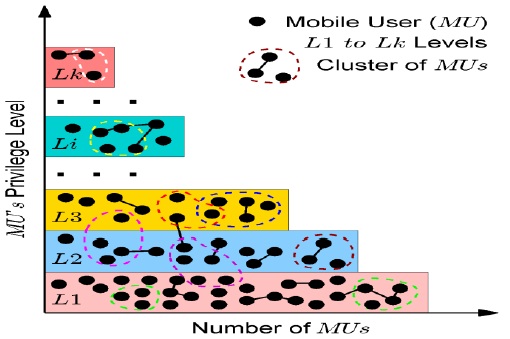
This section discusses a novel k-level data-pricing scheme, denoted as kDP. kDP defines the k number of different MU levels for the pricing of MSs according to the MUs’ privilege value, which depends on their data usage. Furthermore, kDP considers all four forms of data, i.e., PC, D, SMS, and MMS, for the evaluation of MUs’ privilege level. Notably, a relatively high privilege value of an MU promotes the MU at a high level of services.

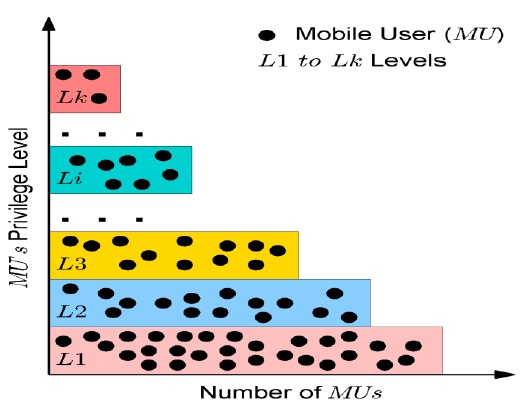
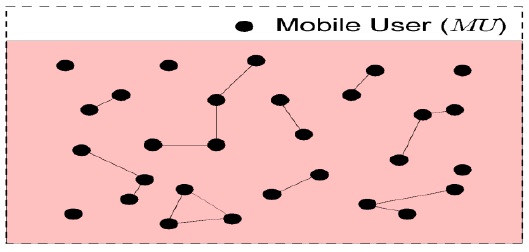
Fig. 2 demonstrates the logical diagram of kDP, which consists of the number of MUs at each level. L1 to Lk represent the low level to high level of MU privileges. In kDP, as the MU earns a high reputation, it has been promoted to a higher privilege level, thereby obtaining a high quality of services at a reduced cost. Notably, the number of users is very small at a higher level as compared to that at a lower level because even a few MUs are sufficiently capable to cross the ‘cutoff’ of a particular level. For example, MUs at L2 have to obtain a sufficient privilege value to cross the cutoff of L2 to L3. kDP considers the cutoff level on the basis of an equal or unequal distribution of the privilege values. We have described both the distributions later in detail.

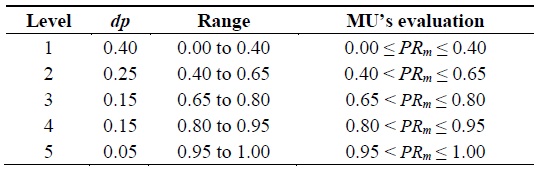
Let us consider that we have k number of privilege levels and n number of mobile evaluation parameters (e.g., PC, D, SMS, MMS, total bill amount, data usage, and payment consistency) with their weight coefficient and distribution period dp. An MU’s privilege value lies between 0 and 1; therefore, the ranges for k-levels also lie between 0 and 1. Once the privilege value for a given MU is evaluated, the level of this MU is decided, and according to its level, the MU obtains the benefits provided by the MSP. Thus, for a given MU m, its privilege value PR_m can be computed as follows:

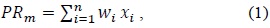
where x_i denotes the normalized value of the i^th mobile evaluation parameter and w_i represents the relevant coefficient of x_i. Here, 0 ≤ w_i,x_i ≤ 1, and For example, for a given mobile user m, we have three mobile evaluation parameters x₁, x₂, and x₃, and their respective values are 0.7, 0.3, and 0.5. Moreover, the values of their related coefficients w₁, w₂, and w₃ are 0.5, 0.3, and 0.2, respectively. Hence, by using Equation 1, we can calculate the privilege value PR_m of m as follows: PR_m = [(0.5 × 0.7) + (0.3 × 0.3) + (0.2 × 0.5)] = 0.54.

For a given set of MUs, the MSP evaluates the set of PR and decides the MU’s level among k levels. Here, the value of k is application specific; hence, the MSP is independent to decide the number of levels in kDP. As the number of levels increases, the MSP provides an increasing number of plans to benefit the MUs. Once k is decided, the MSP performs the range calculation on the basis of one of the following distributions: equal range or unequal range. Each level has a unique range of values to determine whether the MU belongs to that level. At any point of time, a given MU lies in any of the k levels on the basis of the MU’s PR. Notably, in both of the distributions, an increase in the range of the i^th level results in a low utilization of MSs because the data price is fixed for each level by the MSP, and as the privilege level increases, the number of MUs decreases.

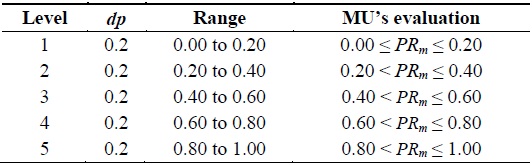
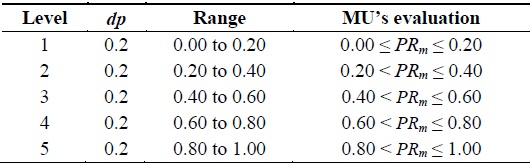
The distribution period (dp) or the length of the range for each level has been computed equally. Hence, dp = (1/k), where k > 0. The value of dp is used for deciding the privilege range for k-levels.

Furthermore, we have 0 ≤ PR ≤ 1; therefore, the range values for each level also lie between 0 and 1 and are distributed according to the value of dp. For example, let us consider that we have k = 5; in this case, the range for each level is computed as shown in Table 1, with dp = 0.2.

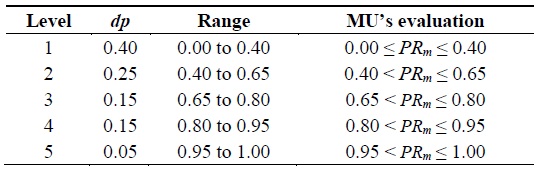
In this distribution, the MSP decides the varied distribution period for each level with the constraint that the sum of all the distribution periods must be equal to 1. Furthermore, no range values are less than 0 or more than 1. Let us consider that dp_i denotes the distribution period of the i^th level; hence, 0 < dp_i < 1 and We have presented an illustrative example of unequal-range distribution with the range of each level in Table 2.

Notably, as per our previous example, for a given mobile user m with the privilege value PR_m = 0.54 (computed using Eq. (1)), the equal-range distribution defines m in Level 3, while the unequal-distribution puts m in Level 2.

Fig. 3 illustrates the relationship tree of the MUs, MSP, and MSs under the kDP scheme. As shown in Fig. 3, MS₁ has been subscribed by MU₁, MU₃, and MU₄, while MS₂ is subscribed by MU₂ and MU₄. Suppose that MU₁, MU₂, MU₃, and MU₄ belong to level L5, L1, L2, and L4, respectively. Further, assume that at levels L1 to L5, the set of plan charges for MS₁ and MS₂ is {$70, $65, $55, $40, $35} and {$100, $80, $60, $50, $40}, respectively. Thus, considering kDP’s privilege-level computation, we calculate the total payable amount for MU₁, MU₂, MU₃, and MU₄ as $35, $100, $65, and $90 (i.e., $40 + $50), respectively. Notably, MU₁ gets benefited more as compared to MU₃ and MU₄.

Observe how MUs dynamically incur the data costs in kDP. The period of recomputation for the privilege values of all MUs in mobile networks is application- and MSP-dependent. The MSP may recomputed the MU’s privilege level fortnightly, monthly, quarterly, and so on, on the basis of the company policies and user requirements. kDP ensures an improvement in data pricing from the perspectives of the company and the customer, while providing an effective “win-win” situation towards efficient data usage for mobile communication.

This section discusses a cooperative peer-to-peer data-pricing scheme, denoted as pDP. pDP defines n number of different MUs to work cooperatively in a peer-to-peer fashion for effectively utilizing MSs at optimal data prices. pDP incorporates the sharing of MSs, which are made up of individual or combinatorial forms of data, i.e., PC, D, SMS, and MMS. In contrast to kDP, the sharing of MSs among MUs leads to effective load balancing in terms of data usage and data pricing for mobile communication. Furthermore, plans become more lucrative to the MUs as they can earn currency by providing MSs to the other MUs in the network. This is analogous to the real-world scenario of a production company and its distributors, which are the MSP and the MUs, respectively, in pDP. Notably, an MU’s roles as a service distributor and as a service consumer are interchangeable; i.e., a given MU may be a distributor for one MS and a consumer for another MS.

Fig. 4 shows the logical diagram of pDP, which consists of a number of MUs. Compared to kDP, pDP does not incorporate the notion of level-based differentiation of MUs, and thus, all MUs obtain MSs at the same cost albeit the individual costs of MSs may differ. In pDP, MSs provided by the MSP are subscribed by MUs and shared with other MUs on the basis of an intra-peer relationship. Therefore, the data pricing for an MS is defined at two stages: original data pricing of an MS (i.e., the MSP’s data pricing), designated as service-level pricing (SLP), and individual data pricing of an MS (i.e., the MU’s data pricing), designated as peer-level pricing (PLP). Here, for a given MS, the SLP is fixed across all MUs, while the PLP may differ from peer to peer in mobile networks, as we assume that all MUs are rational and are interested in increasing their individual benefit, thereby increasing the overall outcome of the mobile communication.

Each MS is associated with a predefined maximum allowed usage by an MU. Suppose that a given MS s has 1 GB of D and 300 PCs, then its subscribed MU is allowed to utilize a maximum of 1 GB of D and 300 min of PC at a fixed cost. On the basis of the MU’s utilization of the MS, we define three cases of service utilization: (i) perfect: s is fully utilized before its expiry, (ii) under: s is partially utilized till its expiry and (iii) over: s is fully utilized before its expiry and further utilization at an additional cost to the MU.

Notably, perfect utilization does not require any cost to be incurred by the MU. Interestingly, underutilization of the MS provides the MU an opportunity to serve as a service distributor and provide the underutilized amount of service data (i.e., in terms of PC, D, SMS, and MMS) to the other MUs, thereby earning money. In contrast, over-utilization of the MS needs the MU to serve as a service consumer in order to request service data at an additional cost from the other MUs in the mobile communication network.

Now, the additional cost charged by an MU to provide the MS to another MU is based on PLP (i.e., peer-level pricing). We consider that PLP = ρ × SLP, where 0 < ρ < 1, to ensure that PLP is always positive and lower than SLP. This is because rational mobile users should benefit by obtaining services from other MUs rather than requesting them from the MSP.

The sharing is also advantageous to the service distributor as the underutilized services are expired and are of no benefit. Hence, the underutilized services should be distributed at a low price in order to reduce the service cost to the peer. pDP ensures that all MSs are utilized at the perfect level, while peers get benefited by the lowering of service prices, thereby increasing the overall outcome of the mobile communication network. Here, the MSP may lose the extra money that it would have received from the MUs who over-utilized the MSs. Hence, pDP only benefits MUs through flexible and collaborative MS sharing and lower data prices. Let us consider a real-world application scenario: two mobile users MU₁ and MU₂ have subscribed to mobile services s₁ and s₂, respectively. s₁ has 2 GB of D for $60 and 500 PCs for $40, while s₂ has 1 GB of D for $40 and 300 PCs for $30 with a service expiry of 30 days each. Hence, the SLPs of s₁ and s₂ are computed to be $100 and $70, respectively, and the calculated per-unit price for s₁ (D, PC) = ($0.03/MB, $0.08/min) and s₂ (D, PC) = ($0.04/MB, $0.10/min). Furthermore, the MSP charges per unit for over-utilization of (D, PC) are ($0.05/MB, $0.15/min), which are the same across all the MSs and MUs.

Suppose that MU₂ over-utilizes a service and is out of data to be used within the expiry time. Therefore, MU₂ requests for extra service data from MU₁, who is supposed to have the remaining 1 GB of D and 150 PCs. Assume that ρ = 0.3 (i.e., 30% of the original cost of MS) and MU₁ provides 500 MB of D and 50 PCs to MU₂. Therefore, the per-unit PLP for MU₂ is computed as s_1:2 (D, PC) = ($0.009/MB, $0.024/min). Therefore, the total PLP cost to MU₂ is $5.7 (= [500 × $0.009 + 50 × $0.024]). If MU₂ uses service data from the MSP at the over-utilization charges, then the service cost would be $32.5 (= [500 × $0.05 + 50 × $0.15]). Hence, MU₂ gets a benefit of $26.8 ($32.5 – $5.7), while MU₁ earns $5.7 from its service distribution. In reality, MU₁ and MU₂ pay $94.3 for s₁ and $75.7 for s₂, respectively. This proves the benefit of an intra-peer relationship.

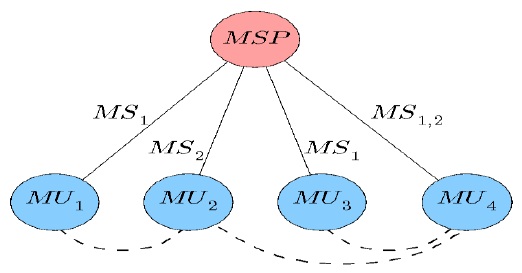
Fig. 5 illustrates the logical relationship among MUs, MSP, and MSs in the case of mobile communication using the pDP scheme. For ease of understanding, we assume the same MSP, MSs, and MUs in the mobile communication network, as discussed in Fig. 3. Here, the plan charges for MS₁ and MS₂ are $70 and $100, respectively, as there is no level consideration for the MUs as in the case of kDP. Further, the difference between the pDP and kDP relationship trees is the connectivity between the peer nodes; i.e., MU₁ is connected to MU₂, while MU₂ and MU₃ are connected to MU₄. The connectivity between the peer nodes demonstrates their cooperative sharing of data services in pDP. For example, MU₁ shared its subscribed MS₁ with MU₂ at the price negotiated between them, while MU₄ shared its subscribed MS₁ and MS₂ with MU₂ and MU₃. Here, MSs may be shared on the basis of partial usage; i.e., a given MU shares its D, PC, SMS, or MMS with other peer MUs through PLP. We consider that the negotiated charges are lesser than the original charges. Further, the sharing amount is 30% of the MS; hence, the data charges are 30% of the total cost of sharing. For example, MU₁ charges 30% for MS₁ to MU₂ on the basis of a 30% data-usage transfer. Similarly, MU₄ shares 20% of MS₁ and 30% of MS₂ with MU₂ and MU₃, respectively. Therefore, the total payable amount for MU₁, MU₂, MU₃, and MU₄ is $49 (=$70 - $21), $135 (=$100 + $21 + $14), $100 (=$70 + $30), and $126 (=$70 + $100 - $14 - $30), respectively. MU₁ benefits more than MU₃ and MU₄.

Here, we considered the notion of cluster, which consists of MUs in a mobile communication network. In this section, we discuss a cluster-based data-pricing scheme, denoted as cDP. In cDP, each cluster is formed from two or more MUs, who are closely related. MUs join the clusters to obtain benefits from the other members of the cluster. Furthermore, cDP is a hybrid scheme, which incorporates the notions of k-level data pricing and peer-to-peer pricing from kDP and pDP, respectively. Moreover, the MS in cDP considers all four forms of service data, i.e., PC, D, SMS, and MMS.

cDP gains the benefits of kDP and pDP as k-level pricing reduces the individual data prices for the MUs and peer-level pricing reduces the collaborative data prices for the MUs. Moreover, each cluster in cDP subscribes to the combined MSs provided by the MSP; such a service plan is provided as a cluster-service subscription, and its charges are defined according to cluster-level pricing (CLP). In cDP, MUs are motivated to exchange their individual service data with others to obtain the data-usage benefit. For example, MU₁ and MU₂ belong to the same cluster. MU₁ has higher utilization of D, while MU₂ requires more PCs; hence, the subscribed MS in the cluster provides an exchange of their individual D and PCs, thereby enabling effective utilization of MSs at reduced costs. The hybrid concept of cDP benefits both the MSP and the MUs as the MSP generates a high revenue from large service plans, while the MUs receives flexibility in terms of their individual service usage at a low cost.

As shown in Fig. 6, cDP has a hybrid structure of kDP and pDP. Fig. 6 shows the same analogy that we discussed for Fig. 2. In cDP, MUs subscribe to MSs as per the “cutoff” level of kDP. However, the MUs get the privilege to share and exchange their individual MSs in a peer-to-peer fashion as discussed in the case of pDP. cDP also incorporates the equal and unequal distributions of kDP as per the specific policies of the MSP.

Observe that the MUs in a cluster may belong to the same or different privilege levels. MUs at a higher level provide more benefit to the cluster, as their subscribed MSs are costeffective as compared to those of the lower-level MUs in the cluster. Furthermore, a given MU may associate with more than one cluster in a mobile network. This is related to the real-world scenario that a person is associated with two different cluster plans, i.e., one for home usage and the other at work. Thus, cDP provides flexibility to balance the service data usage for an MU across all the clusters to which the MU belongs. Moreover, a member MU of a cluster may share its service data with other independent peers in mobile networks to generate revenue for its own cluster. This enables MUs in a cluster to sell their MS data to other MUs. Furthermore, two clusters can be associated with one another through their MUs. For example, two social network friends may belong to two different home plans, but they may share/exchange data.

As in the cases of kDP and pDP, we have found a logical relationship among MSP, MUs, and MSs for cDP; it is shown in Fig. 7. Here, the MUs are clustered, and they exchange their service data within the cluster or outside the cluster, depending on the total cluster usage. For example, MU₃ is associated with MU₄ for exchanging MSs. We consider that the computation for data pricing in cDP is a combination of the kDP data-pricing computation and pDP’s PLP (i.e., peer-level pricing) computation.

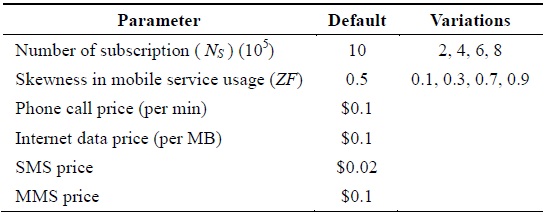
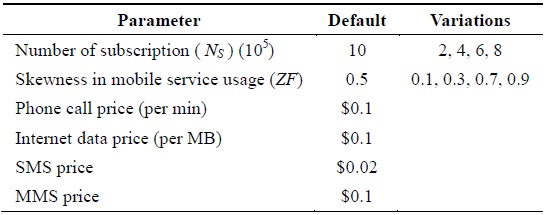
This section reports our performance study conducted using our own simulator for MobPrice. All our experiments have been performed for all our schemes, namely the kDP, pDP, and cDP schemes presented in Sections IV, V, and VI, respectively. Moreover, Table 3 summarizes the parameters used in our performance study.

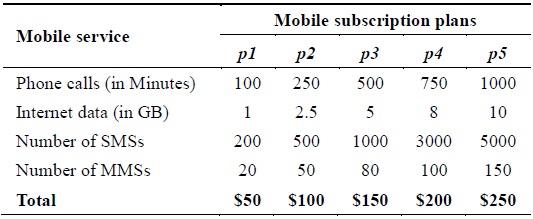
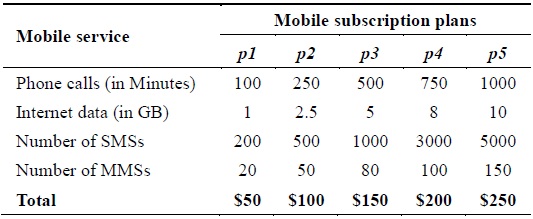
Our experiments consider a total of 1 million mobile subscriptions for all four forms of services, namely phone call (PC), Internet data (D), short message service (SMS), and multimedia message service (MMS). Each subscription is associated with one of the five mobile subscription plans {p1, p2, p3, p4, p5} defined in Table 4. Notably, each mobile subscription plan (p) consists of fixed usage for MSs. For example, as shown in Table 4, p1 costs $50, which includes 100 min of PCs with 200 SMSs and 20 MMSs along with 1 GB of D usage for a month. Hence, we assume that each p is applicable on a monthly basis; i.e., each billing cycle has a period of 1 month. Furthermore, the overusage for each of the services will be charged according to the prices described in Table 3. For example, if a given mobile user subscribes to p1 and has 150 PCs, then the over-usage of 50 PCs costs $5 at the rate of $0.1/PC.

Here, the allowed usage is described as an upper limit of the usage of MSs for a given subscription plan, while the actual usage is defined as the total usage of MSs per billing cycle. Notably, the actual usage may not always be equal to the allowed usage; i.e., under a given subscription plan, few services may be over-used, and the others may be underused. Hence, over-usage means actual usage > allowed usage, and under-usage means actual usage ≤ allowed usage.

We considered the performance analysis based on the communication price per user. Here, the communication price (CP) is defined as the total price that has been paid by a given MU to the MSP. CP may vary per user on the basis of the user’s subscription and its over-usage of the MSs. Hence, the average communication price (ACP) is computed as the total charges paid by all users in the system divided by the total number of subscriptions. Thus, ACP is computed as follows:

where p_i denotes the price of a mobile subscription plan subscribed to by mobile user i and p_ou represents the price of i’s over-usage, while N_S represents the total number of subscriptions. Furthermore, we considered the average effective utilization (AEU) of MSs on a per-user basis. Here, the utilization of an MS is considered to be the percentage of the difference between over-usage and under-usage for a given MU. Thus, AEU is computed by using the following equation:

where u_i denotes the usage difference of MSs under i’s subscribed plan. For example, two mobile users m₁ and m₂ share data services. Suppose that m₁ has 1000 MB of D to be used under its subscription plan, but it has used only 500 MB of D. Thus, the under-usage of D is 500 MB. Now, m₁ gives 300 MB of D to m₂ at the negotiated price; hence, m₁ ’s usage of D becomes 800 MB. Thus, u₁ becomes 30% (i.e., (800 MB – 500 MB)/1000 MB × 100).

As reference, we consider the fDP (which stands for fixed data pricing) scheme, which does not provide any lucrative pricing to subscribe to any MSs. Similar to kDP, pDP, and cDP, the MSP offers this pricing scheme to the MUs. In fDP, an MU subscribes the service exactly in the same manner as in kDP, pDP, and cDP. The only difference is that the MU gets the service without any flexibility of sharing any MSs among other MUs. Thus, it has to use only the subscribed plan with the fixed rates offered by the MSP. We also assume that for the pDP and cDP schemes, the sharing prices (or negotiating prices) for MSs are 50% of the actual prices from the MSP; i.e., if the MSP charges $0.1 per PC, then the sharing price of PC among mobile peers would be $0.05.

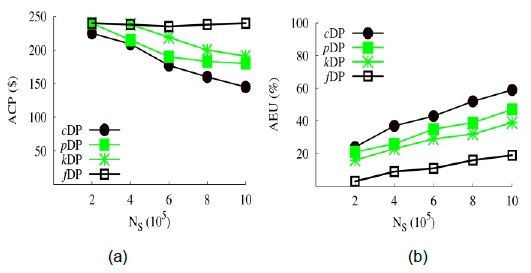
We conducted this experiment using the default values of the parameters in Table 3. Fig. 8 depicts the results. As the number of subscriptions increases, ACP decreases sharply for both pDP and cDP because of the flexibility of intra-peer service sharing. Moreover, ACP decreases slightly for kDP as compared to fDP because of kDP’s effective scaled-pricing mechanism, which reduces the bit price for each user, thereby reducing the overall communication price in MobPrice. However, in kDP, the decrease in ACP is comparatively low because of the cutoff restrictions of the levels. In kDP, although the prices are distributed among the levels, the user has to cross the cutoff for a level in order to take advantage of the high-level subscription benefits. In contrast, fDP has a comparable performance in terms of ACP because of its fixed pricing model and its firm nature for service distribution irrespective of the actual usage, thereby resulting in high communication prices and low utilization.

Recall that the prices of subscription plans are fixed by the MSP. Hence, AEU is inversely propositional to ACP. Considerable flexibility of a service exchange results in maximum utilization of this service per user, thereby minimizing ACP. The most effective distribution pattern of a service results in minimum ACP and maximum AEU, which further benefits MobPrice and improves the price/bit. fDP exhibits relatively constant ACP because of its firm nature for service distribution and pricing. Hence, AEU remains relatively low for fDP because it does not allow intra-peer service sharing.

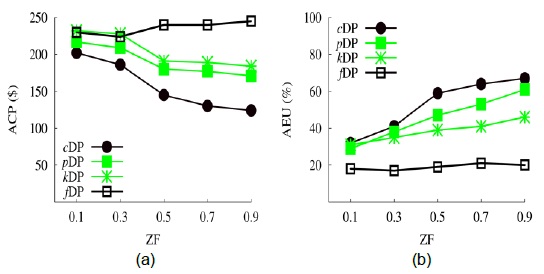
The skewness ZF of the MS usage across all MUs in the system is defined as the usage distribution of the MSs among mobile subscriptions. The value of ZF = 0.1 depicts that the MS usage is comparable across all MUs, while ZF = 0.9 denotes a highly skewed scenario in which a few MUs may have a relatively high utilization of one of the services. This creates an impact on the communication prices as well as the effective utilization of the MSs at the system level as service usage is highly skewed and distributed.

Fig. 9 depicts the effect of the variations in ZF across N_S, which represents the number of mobile subscriptions. As ZF increases, ACP decreases for all the proposed schemes except fDP. This is because of the effective utilization of the MSs across all the MUs. Moreover, cDP outperforms pDP and kDP because of its effective sharing of MSs across the subscription as a cluster of mobile peers may have different requirements of MSs. This improves the utilization at reduced costs of subscribed services. Similarly, AEU increases for all the proposed schemes except fDP, as the high skewness defines the impact of a few prominent MUs on the system, which is advantageous for the collaborative usage of MSs. Moreover, this shows that the real-world scenario has a highly skewed distribution of MS usage as a few users use more D than PCs; e.g., tablet users need more D than PCs or SMSs.

In this paper, we proposed MobPrice, a platform for dynamic data-pricing schemes. In MobPrice, MUs are inspired to subscribe to MSs according to the flexibility of dynamic data sharing at a reduced cost. The core objective of MobPrice is to achieve optimal usage of MSs at optimal prices. Moreover, the intra-peer relationship enables MUs to exchange their individual MSs at a reduced cost. On the basis of the different levels of data pricing and the intra-peer relationship, we have proposed three data-pricing schemes, namely k-level data pricing (kDP), peer-to-peer data pricing (pDP), and cluster-based data pricing (cDP) for all four forms of service data, namely phone calls, short/multimedia messages, and Internet data, for mobile communication. Moreover, our performance evaluation shows that our schemes are indeed effective in improving MobPrice functionality in terms of maximizing the overall service subscription and minimizing the price/user for a subscribed service.

In the future, we intend to extend our work by incorporating social networking and crowdsourcing for data pricing in the field of mobile communication. The social network increases cooperativeness, which results in an effective dynamic data-pricing strategy, thereby reducing the overall data costs.