정보가 급증함에 따라 큰 용량의 데이터를 전송해야 할 경우가 있다. 빅 데이터 전송 기술은 큰 용량의 데이터를 전송할 때 필요하다. 본 논문은 빅 데이터를 최적화된 속도로 전송하기 위해 GridFTP의 주된 기능인 PCP를 사용하며 또한 PCP 값을 예측하는 알고리즘을 개발한다. 또한, TSK 퍼지 모델을 적용하여 PCP에 따른 최적화된 전송률을 측정하는데 사용된다. 따라서, 제안된 TSK모델을 이용한 PCP 예측 알고리즘은 본 논문의 우수성을 입증한다.
Big data transfer technologies have been in the spotlight with three properties of the velocity, volume and variety.
As these technologies are actively researched, areas of computer network researching data transfer technology are also emerging as important topics. Although FTP is being used in order to allow the transfer of the data among the computers, it may decrease the throughput of data transfer especially in big data transfer. In order to solve this problem, GridFTP [1] is popularly used to achieve an optimal throughput to transfer the large amounts of data by enhancing security, transfer speed and reliability of data transmission. Existing work has tried to find optimal values of Pipelining, Concurrency and Parallelism (PCP) by using historical PCP datasets. Hence, the author is willing to propose an efficient algorithm with Takagi-Sugeno-Kang (TSK) fuzzy model [2,3] to predict optimal values of PCP and the throughput. PCP includes the following functions.
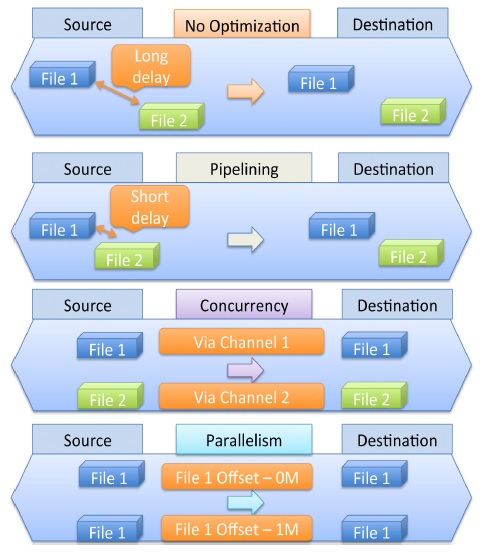
Pipelining is a method of transmitting files continuously without waiting for a response signal for the previous transmission. Concurrency usually transmits various files via different channels at the same time. Parallelism is a method of transmitting different parts of the same file via multiple parallel data channels at the same time. Therefore, three PCP functions are very useful for large-scale data transmissions.
GridFTP [1] can improve throughput by optimizing PCP values which are manageable major functions depending on file size, number of files, bandwidth, round trip time (RTT) and buffer size. Prior studies [4-10] suggested some algorithms for finding the optimal combination of parallelism. However, a drawback of these studies is that throughput of data transfer may decrease due to overhead, which could occur when the conventional algorithm finds the optimal combination of PCP values by using the information gained by transferring sampling files through network channel.
Hence, this paper suggests an efficient algorithm for predicting the optimal combination of PCP based on fuzzy model; this is appropriate for certain circumstances of data transfer based on the measured abundant experimentation datasets which contain throughput values depending on PCP in different testbed environments. In addition, the author designed a model of predicting the throughput of data transfer under the optimal combination of PCP using the processed experimentation dataset by TSK fuzzy model.
Abundant PCP experimentation datasets measured in various testbeds contain more than seventeen factors such as file size, number of files, bandwidth, round-trip time, buffer size, pipelining, concurrency, parallelism, throughput, transfer duration and so on. The system will be complex and difficult to interpret because each factor has a non-linear relationship with the throughput and other factors. The PCP background is designed in Fig. 2.
In this paper, the author used clustering, which is a data classification algorithm that identifies the nature of PCP experimentation dataset and specially contains the concept of fuzzy to reflect a more specific characteristic of the data. The author designed a model of predicting the highest throughput of data transfer under the optimal combination of pipelining, concurrency and parallelism based on PCP experimentation dataset. The TakagiSugeno-Kang fuzzy model [2,3] can approximate the very complex non-linear system based on fuzzy rule-based inference.
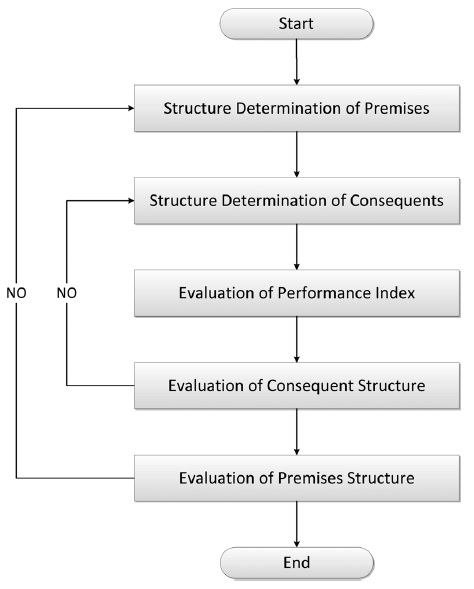
2.1. Takagi-Sugeno-Kang Fuzzy Model
TSK Fuzzy Model is a method of inference based on the fuzzy rule for approximating the complex non-linear system. After creating several rules by dividing input space into fuzzy area, which infers final output by applying fitness into each rule. Here are the steps of the procedure of TSK Fuzzy Model (Fig. 1).
The proposed algorithm finds the most similar data by comparing certain input data with the existing abundant datasets. Most similar data is determined by the data that have the lowest sum of error rate by comparing factors of input data with factors of data in the dataset. In addition, the maximum operators were added in order to consider the factor that contains the outlier.
The proposed algorithm uses the following steps to find optimal PCP values. First, each error is calculated by comparing each of the factors of the data in dataset with each factor of the input data. Second, the algorithm calculates the maximum value on each factor. Third, the algorithm finds the error rate by dividing the maximum value of each factor for each factor in error. Fourth, the algorithm calculates the sum of error rate (SumER) for each data. Fifth, the algorithm calculates the maximum value (MaxER) for each of the error rate data. Sixth, the algorithm calculates the final error rate by combining SumER and MaxER using weight coefficient. Finally, the algorithm finds the minimum value out of final error rate and corresponding data number is determined as most similar data with input data.
The above comparison algorithm is a method of comparing each error rate. However, several factors need to be taken into account simultaneously for one data. If the scale of range of each factor is different, then the comparison method cannot determine the most similar characteristics of data. The proposed algorithm is able to compare characteristics of data by compensating for the differences of range for each factor, using rate of error in the case of several factors exist in data.
Hence, they are useful characteristics for comparing data that contains various scale factors. Therefore, the author applied the concept of the maximum operator to error rate to control for the amount of removal of the outlier.
Finally, compared value is calculated by the total amount of the sum of the error rate multiplied by the weight coefficient and maximum value of error rate multiplied by the weight coefficient. If the weight coefficient is close to 1, then it is difficult to remove the outlier because it is a total comparison method. On the other hand, if weight coefficient is close to 0, then it is more likely to remove the outlier because it is a partial comparison method. The weight coefficient can be used by adjusting to appropriately find most similar characteristics of data.
The author applied the proposed algorithm to PCP experimentation dataset that contains data transfer throughput depending on file size, number of files, bandwidth, round trip time, buffer size, pipelining, concurrency and parallelism generated from various testbeds. Input data is the data corresponding to certain circumstances of file transmission. The author compared the characteristics of input data with characteristics of data in a PCP experimentation dataset and determined the most similar characteristics of data and determining the PCP values of corresponding data number as an optimal combination of pipelining, concurrency and parallelism for certain circumstance of file transmission.
In this experiment, the author applied the most effective five factors to throughput of data transfer such as file size, number of files, bandwidth, round trip time and buffer size in the proposed algorithm. Also, it is essential to preprocess the PCP experimentation dataset before applying the proposed algorithm to dataset.
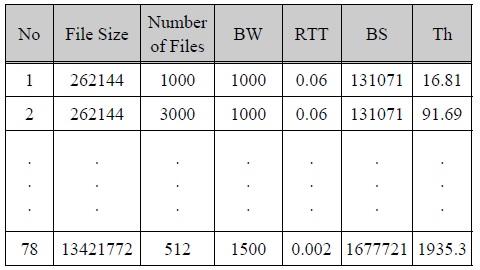
PCP experimentation dataset contains many data that have the same values in file size, number of files, bandwidth, round trip time and buffer size. However, PCP values and throughput values are different. Therefore, a preprocessed experimentation dataset is constructed by extracting each data of highest throughput in all possible cases of the values is same in factors such as file size (Bytes), number of files, bandwidth (BW, Mbps), round trip time (RTT, seconds), buffer size (BS, Bytes) and Throughput (Th, Mbps).
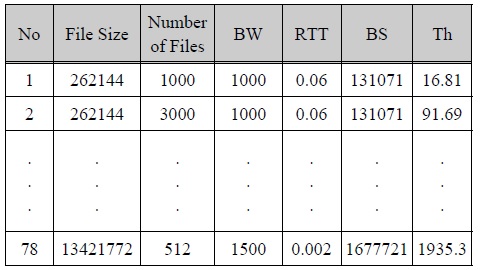
전처리 실험 데이터
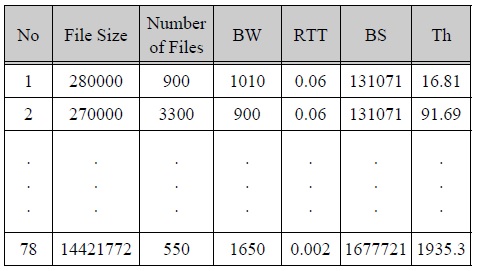
Testing dataset is randomly constructed within the error of 10% with the processed experimental dataset.
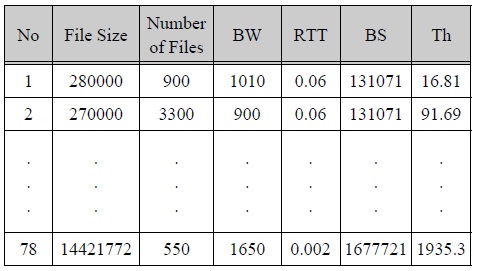
테스팅 데이터
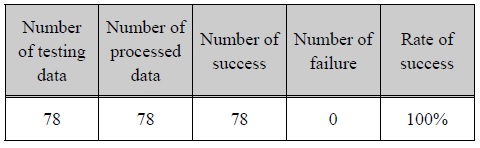
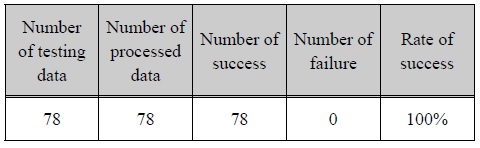
실험결과
The result of the experiment shows highly accurate determination capability, though the range of each factor is very different.
4.2. TSK fuzzy model for predicting throughput under optimal combination of PCP
A prior preprocessed experimentation dataset is used as training data in design of TSK Fuzzy Model. Also, a testing dataset is constructed by extracting each data with the second highest throughput in the same value in file size, number of files, bandwidth, round trip time and buffer size from original PCP experimentation dataset.
In this paper, the author predicted an optimal combination of pipelining, concurrency and parallelism (PCP) for certain circumstances of file transfer such as accruing overhead, network saturation, based on experimental dataset measured by various testbeds. Hence, it would be feasible to transfer large-scale data in optimal throughput with GridFTP by using optimal combination of PCP.
In addition, the author designed a model for predicting throughput of file transfer under the optimal combination of PCP by using TSK fuzzy rule based inference. In future work, the author will optimize weight of error rate in the proposed algorithm based on objective function. Therefore, the new optimization algorithm will provide more efficient way and accomplish to find optimal values of PCP and throughput.