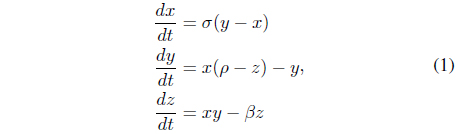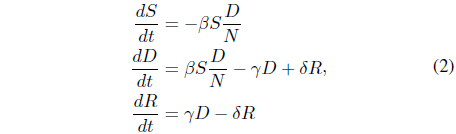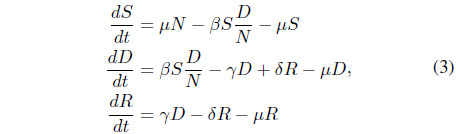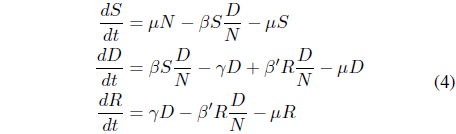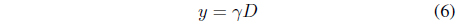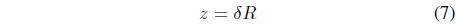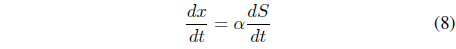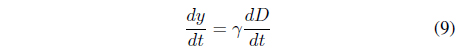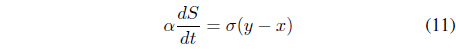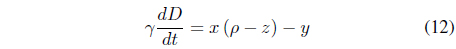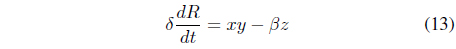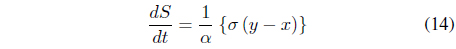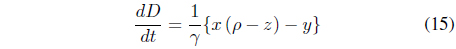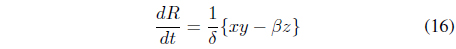In the last two decades, chaotic dynamics have been widely used in real-world applications such as biological systems [1], brain modeling [2], weather modeling [3], vibration modeling [4], mechanical and electrical engineering [5,6], control and synchronization [7,8,19], robotics [9,10], and more [12-15,20,21]. Currently, it is an active area of research by many in biology, physics, sociology, psychology, physiology, and engineering. However, this research is not only performed in natural sciences but also in the social sciences, including politics, economics, and the prediction of societal events composed of various addiction problems [12,18,19].

Addictions caused by tobacco, drugs, games, shopping, and the Internet are serious problems in our current society and many researchers are interested in treating and curing these addictions. Due to the different nature of each addiction, each symptom differs dramatically from one to the other. Therefore, it is not so easy to define encompassing symptoms for all the addictions mathematically [16]. Tobacco addiction has been subject to intense investigation by medical research groups. However, they mainly approach the tobacco addiction epidemiologically rather than mathematically. Therefore, it is necessary to develop a mathematical model of nonlinear phenomena in addiction of tobacco.

In this paper, we propose a dynamic model of tobacco addiction that originates from the dynamics of tobacco use, recovery, and relapse [17]. In order to make an addiction model of tobacco, we try to modify and rescale from the existing chaotic tobacco model and Lorenz model. By using this information, we derive a new tobacco addiction model mathematically. Finally, we obtain periodic and chaotic motion from the addiction model of tobacco. We say that periodic motion and quasi-periodic motion are related to the pre-addiction stage or recovery stage, respectively. Quasiperiodic and chaotic motion are related to the addiction stage and relapse stage, respectively.

The mathematical models of the Lorenz system proposed by Edward L. Lorenz describe various dynamical models of weather systems. The formulation of the Lorenz system is given by the following Eq. (1).

where sigma is called the Prandtl number, which is the ratio of momentum diffusivity (kinematic viscosity) and thermal diffusivity; ρ is the Rayleigh number, which is determined by the heat transfer, primarily in the form of conduction or convection; and β is a geometric factor. The typical values of these three parameters are σ = 10, ρ = 28, β = 8/3; x is proportional to the intensity of convection motion; y is proportional to the temperature difference between the ascending and descending currents; and z is proportional to the distortion of the vertical temperature profile from linearity.

Carlos Castillo-Garsow et al. [17] proposed mathematical models for the dynamics of tobacco use, recovery, and relapse.

They described the general model for drug abuse, vital dynamics, and nonlinear relapse. From these mathematical models, they found the parameter value by using stability theory.

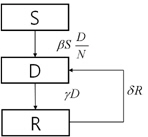
From the model proposed by Carlos Castillo-Garsow et al. [17], a general mathematical model for drug abuse is shown as Figure 1 and can be represented as s Eq. (2).

where S is the total number of individuals in a given population that are susceptible to becoming regular drug users. D is a habitual drug user in that population, and R is the number of people recovered from habitual use. The parameters β, γ, and δ are per capita influence rate, recovery rate per habitual drug user per unit of time, and relapse rate per recovered individual per unit of time, respectively.

Because Eq. (2) assumes a constant population, we need to consider constant mortality rate, following as Eq. (3).

where μ is the constant mortality rate.

The previous two models did not provide the mechanism for the relapse process. We consider a similar peer pressure mechanism for relapse of recovered individuals. Eq. (4) represents relapse of recovered individuals.

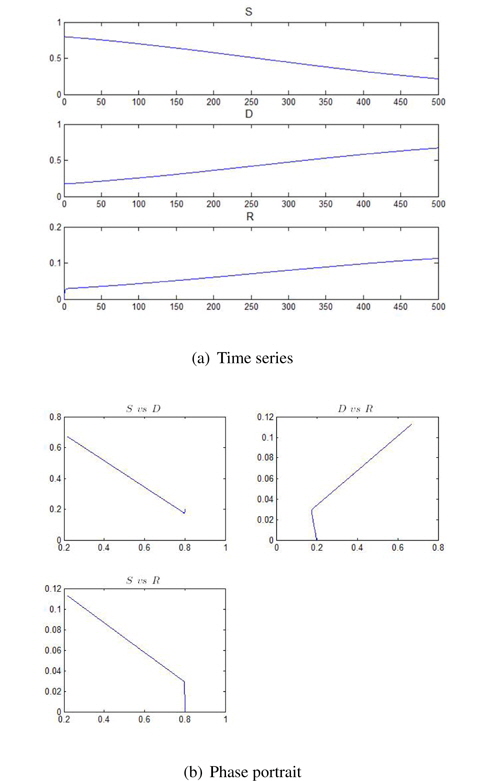
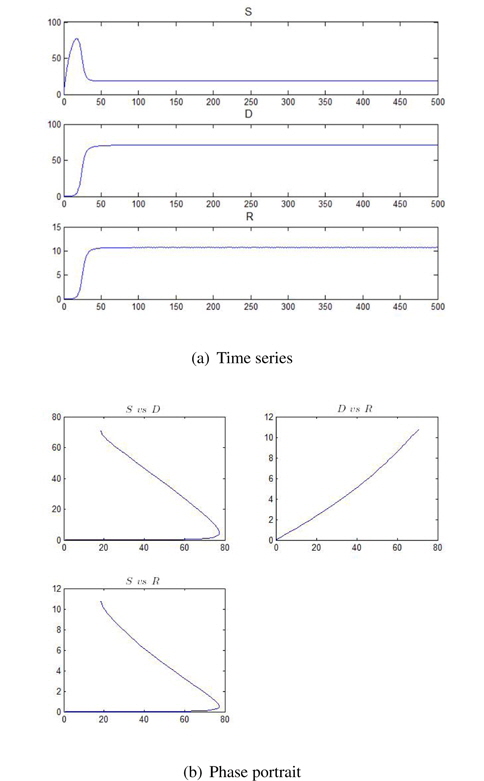
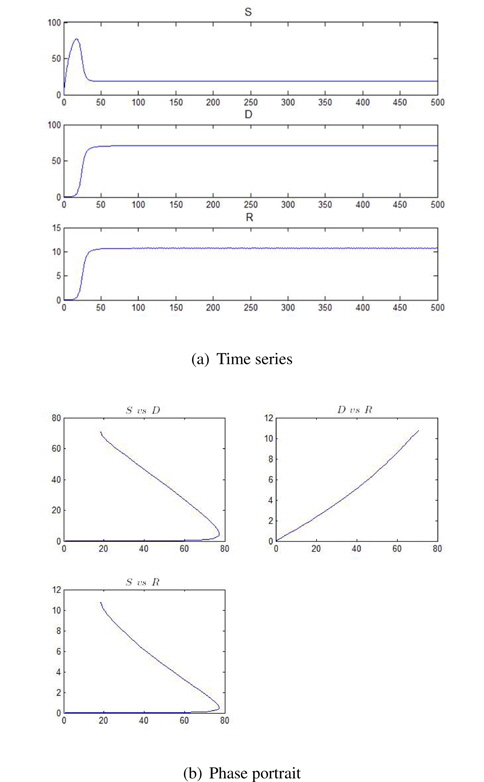
In order to derive chaotic or nonlinear phenomena from Eqs. (2) and (3), we need to modify these equations. From Eqs. (2) and (3), we obtain a solution, which is shown in Figure 2 and 3. Figures 2 and 3 show time-series and a phase portrait for Eqs. (2)-(4), respectively. Here, we use N = 100, δ = 0.89, γ = 0.15, and β = 0.625 for Eq. (2), N = 100, μ = 0.1, δ = 0.89, α = 0.4, γ = 0.15, and β = 0.625 for Eq. (3), and N = 100, μ = 0.1, δ = 0.89, α = 0.4, γ = 0.15, and β = 0.625, R = 2.5 for Eq. (4). We recognize that there is no vibration or fluctuation because Eqs. (2) and (3) lack a nonlinear term.

To make a similar Lorenz equation such as Eq. (1) from Eq. (2), we need parameter rescaling and some substitution. To do this, we rescale each parameter x, y, and z, as described in Eqs. (5)-(7).

When we take derivatives of Eqs. (5)-(7), we obtain Eqs. (8)-(10).

We can set Eq. (1) equal to Eqs. (8)-(10). The new equation can be written as Eqs. (11)-(13).

From Eqs. (11)-(13), we can rearrange a new dynamic equation for tobacco use, recovery, and relapse, as shown in Eqs. (14)-(16).

In order to display nonlinear phenomena from Eqs. (14)–(16), we define each parameter in the previously shown equations to find periodic motion and chaotic motion.

From Eqs. (14)-(16), after assigning parameter values for α, γ, and δ, we varied σ, ρ, and β. As a result, we obtained various time series, phase portraits, and Poincaré for the pre-addiction stage of tobacco, as shown in Figure 5 and 6. The pre-addiction stage has a periodic motion, as with the following:

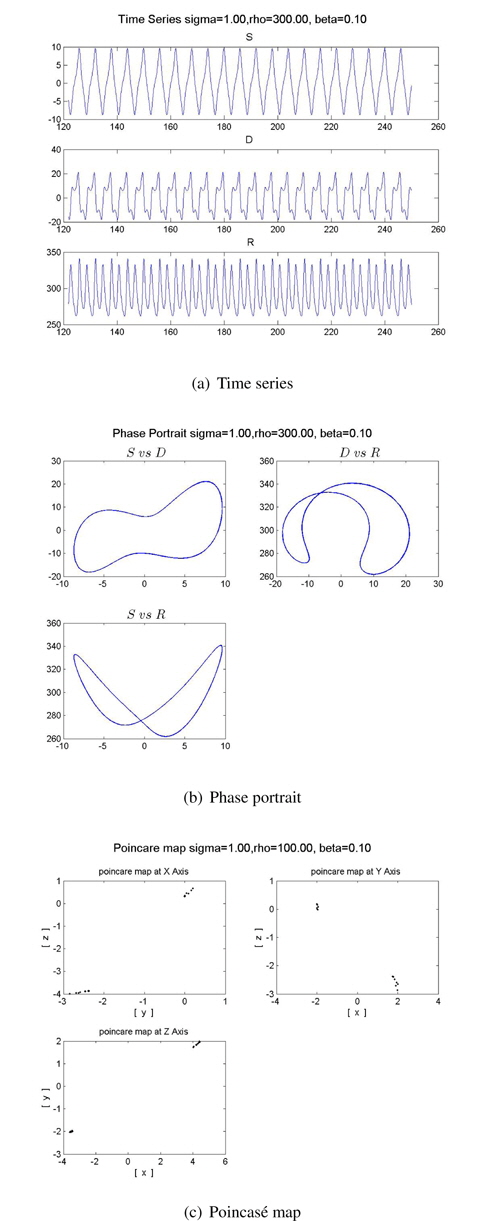
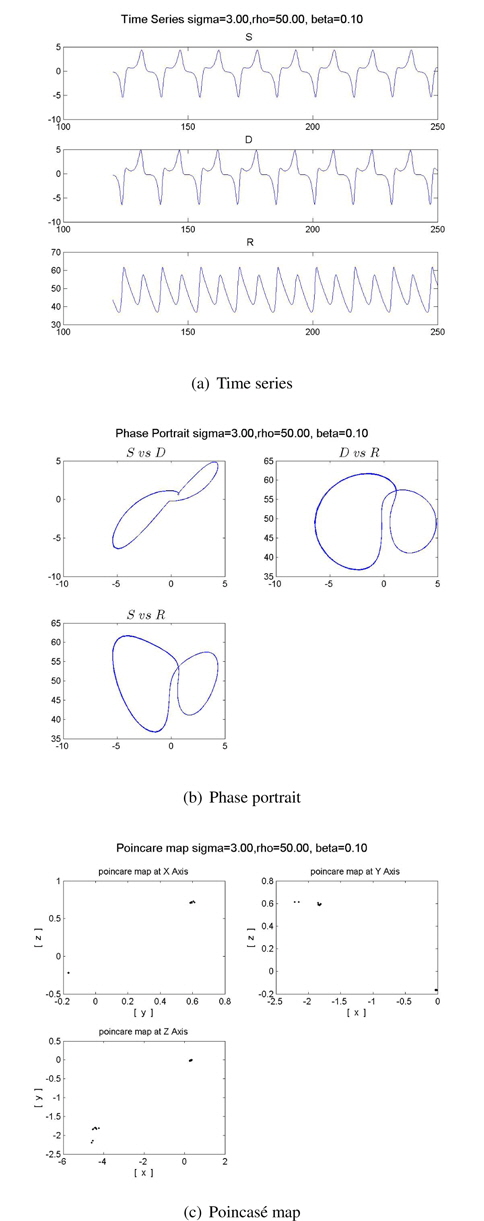
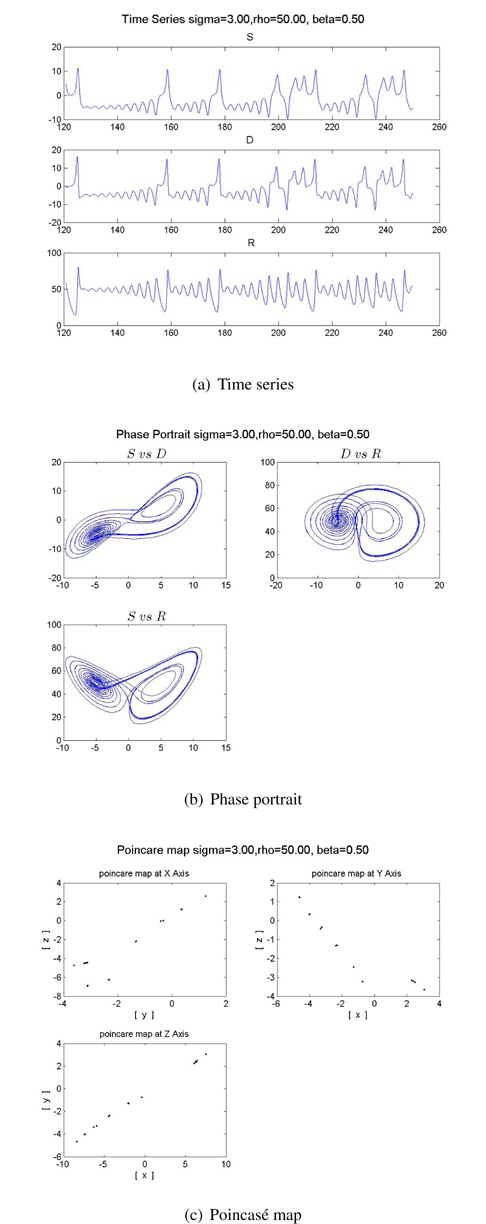
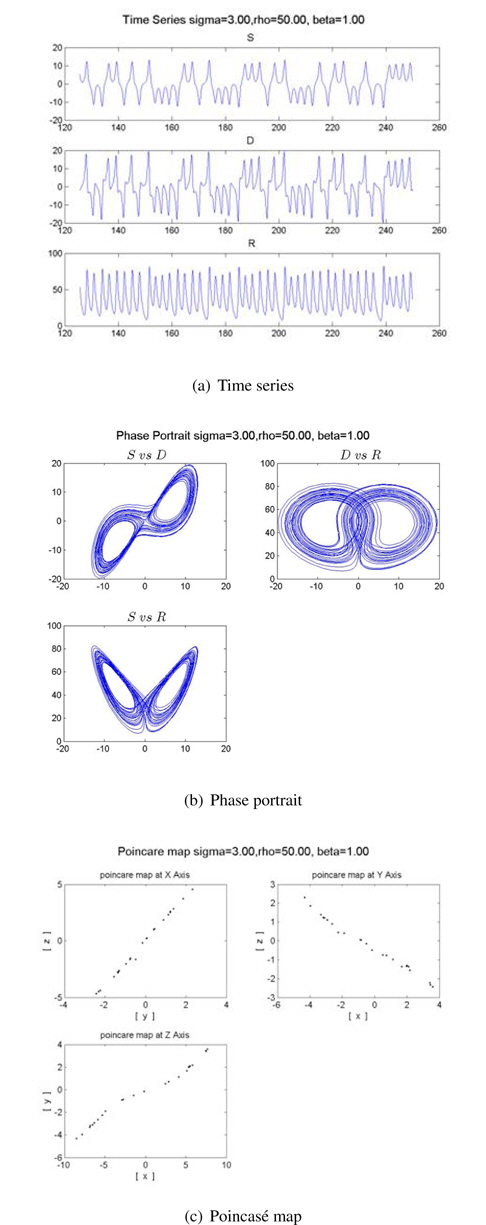
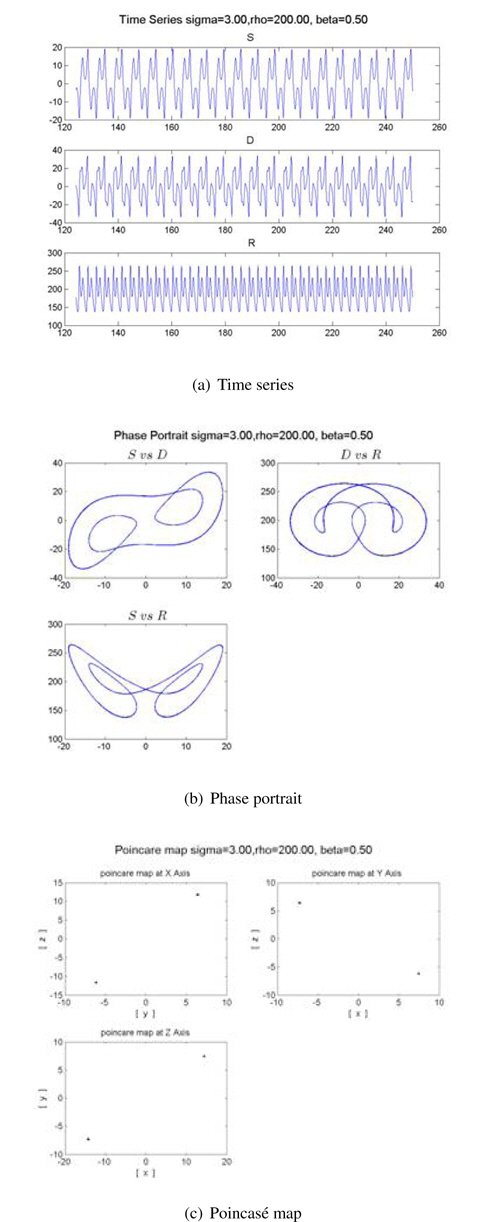
We obtain various time series, phase portraits, and Poincaré maps for the addiction stage of tobacco as the parameters vary. These are shown in Figures 7 and 8. These addiction stages show chaotic motions such as quasi-chaotic and chaotic attractor.

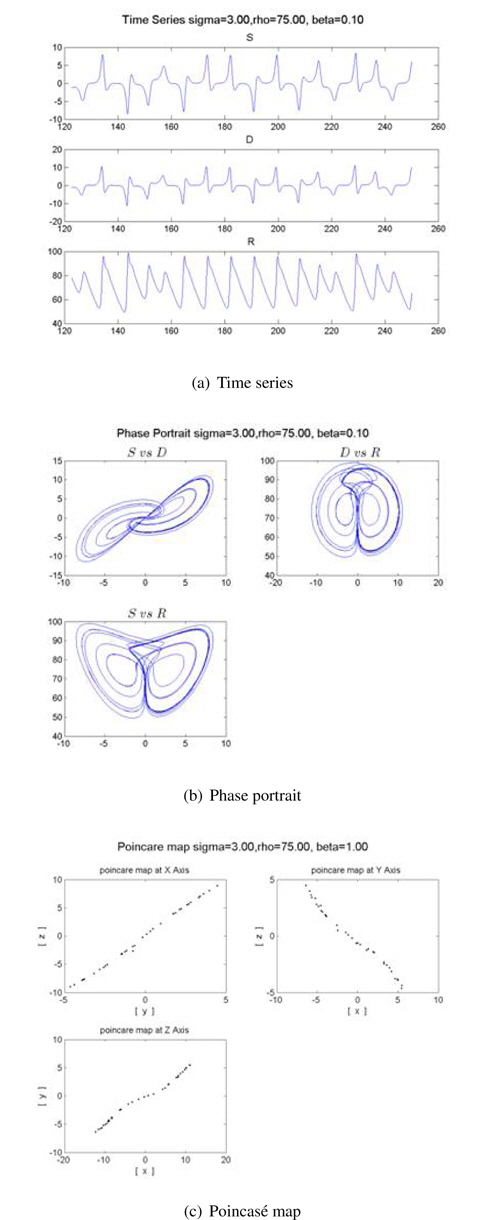
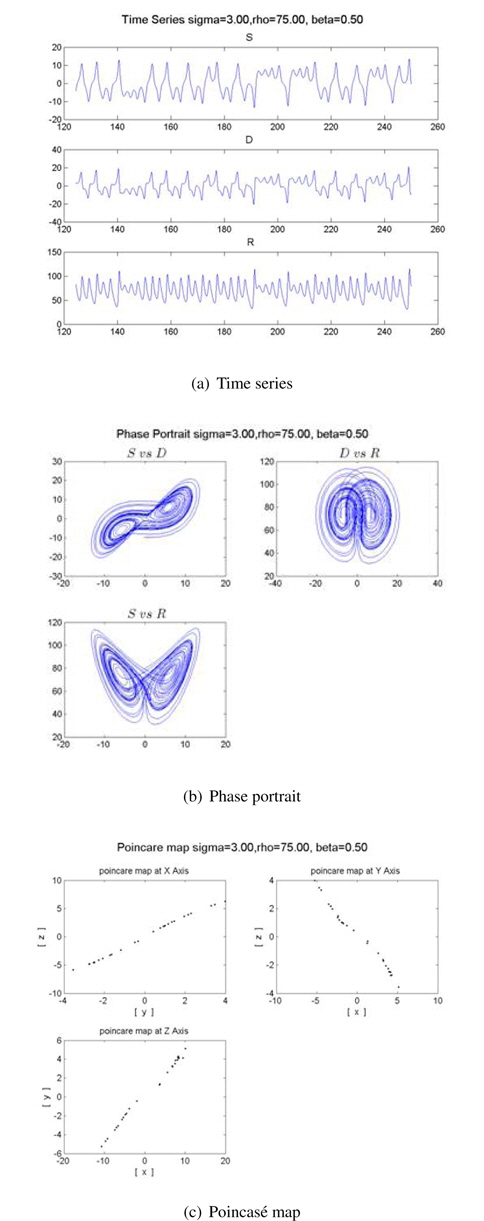
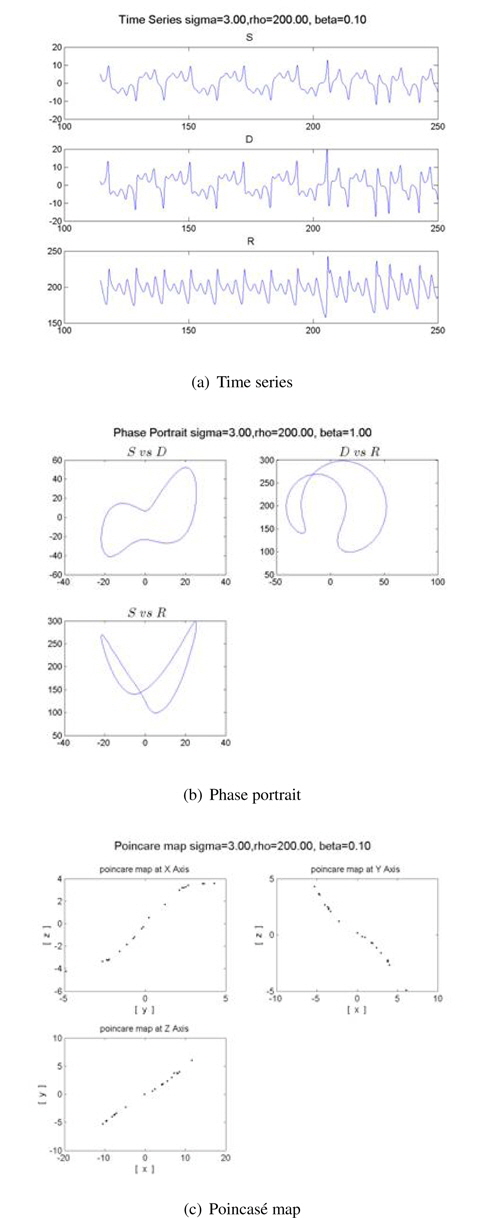
We also obtain another time series, phase portrait, and Poincaré map for the recovery stage of tobacco, as shown in Figure 9. The recovery stage has a quasi-periodic motion unlike the chaotic attractors of Figures 7 and 8. We also varied parameters of σ, ρ, and β, and obtained another phase portrait for the re-addiction stage of tobacco, as shown in Figure 10. The re-addiction stage displays chaotic motion well.

When we change the parameter valuesσ, ρ, and β accordingly, we obtain the relapse stage of the tobacco model, as shown in Figure 11. We obtain recovery and complete the recovery stage of tobacco, as shown in Figures 12 and 13, as we adjust more parameter values accordingly. Figures 12 and 13 represent periodic motion of the complete recovery stage for an addiction.

We proposed a tobacco addiction model by rescaling parameters from the existing tobacco model and the Lorenz system. The mathematical addiction model of tobacco is organized by a third-order differential ordinary system. It is similar to the Lorenz system because it is derived from the system.

From the tobacco addiction model, we obtained periodic motion, quasi-periodic motion, quasi-chaotic motion, and chaotic motion. These motions correspond to pre-addiction or complete recovery, recovery or re-recovery, and the relapse and addiction stages, respectively.

In the future, we need to find detailed roles for each parameter in the addiction model of tobacco that we devised in order to control and treat the addiction status in humans.