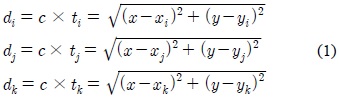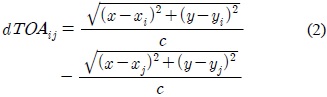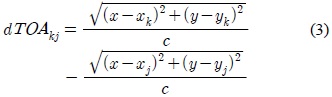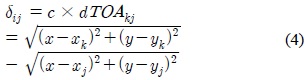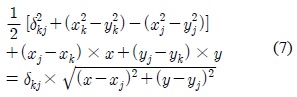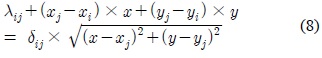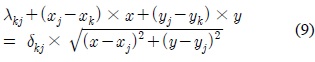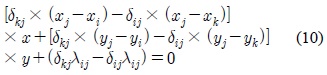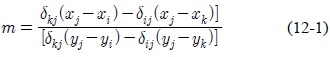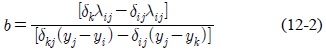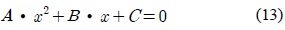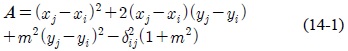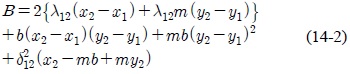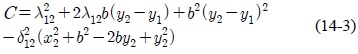선박 환경에서 TDOA 기법에 의한 위치 추정 방법

doi:10.6109/jkiice.2015.19.8.1934

OA학술지
Journal of the Korea Institute of Information and Communication Engineering

선박 환경에서 TDOA 기법에 의한 위치 추정 방법 A Location Estimation Method Using TDOA Scheme in Vessel Environment

DOI : 10.6109/jkiice.2015.19.8.1934
Publish: Journal of the Korea Institute of Information and Communication Engineering Volume 19, Issue8, p1934~1942, 31 Aug 2015

ABSTRACT

선박 환경에서 TDOA 기법에 의한 위치 추정 방법

An estimation problem in the environment which GPS signals do not reach, should be solved by employing an indoor location estimation scheme. Location estimation schemes for indoor environments generally include the AOA, TOA, RSS, Fingerprint, and TDOA. For a ship environment where there exist many spaces enclosed by iron plates, the TDOA scheme is appropriate because location estimation is usually performed at a closed range. In this paper, we address the problem of estimating the location of a terminal under the ship environment. The problem of location estimation by using the TDOA is presented in detail, and then an algorithm for applying the estimation to the ship environment is proposed. Finally, the proposed algorithm of location estimation in a ship by the TDOA scheme is verified through simulations from three viewpoints.

KEYWORD

선박환경 , 위치추정 , Detection Process , TDOA , WLAN

본문

Collapse all

Ⅰ. 서 론

GPS(Global Positioning System) 신호가 도달하지 않는 환경에서 위치를 추정하는 문제는 지금까지 많은 연구가 이루어져 왔다[1-4]. 일반적으로 실내 환경에서 위치 추정은 여러개의 AP(Access Point)를 직교 배열로 배치하여 위치를 찾고자 하는 단말기의 신호를 이용하여 이루어진다. 이러한 방법은 크게 AOA(Angle of Arrival), TOA(Time of Arrival), RSS(Received Signal Strength), Fingerprint, TDOA(Time Difference of Arrival) 방식이 있다. 먼저 AOA 기법은 두 개 이상의 AP를 써서 AP로부터 단말기로 오는 신호의 방향 θ₁, θ₂, ⋯ θ_n을 추정하여 단말기의 위치를 추정하는 방법이다[5-8]. 다음으로 TOA 기법은 단말기와 AP간의 전파 전달시간을 구하여 교차되는 지점을 찾아 위치를 추정하는 방법이다[9]. 또한, RSS 기법은 전파가 거리에 따라 일정하게 감소하는 특징을 이용하여 위치를 추정하는 방법이고[10], Fingerprint 기법은 확률적 모델링에 의한 위치 추정 방법으로 노이즈 및 주위 환경정보를 이용하여 위치를 추정하는 방법이다[11,13]. 마지막으로는 TDOA 기법은 단말기로부터 AP까지의 신호의 전파시간을 구하여 임의의 AP를 기준으로 다른 AP간의 시간차를 구해 추정 문제를 푸는 방법이다[12].

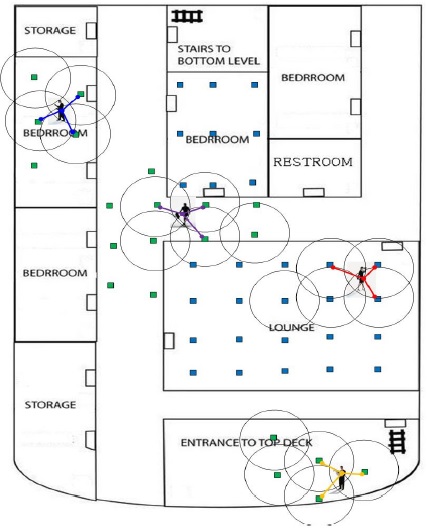
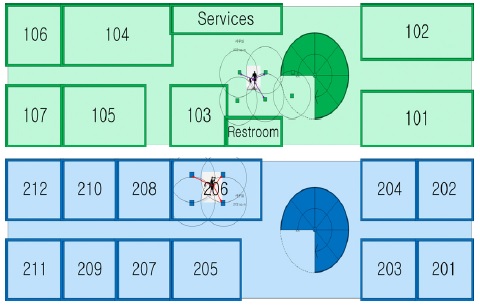
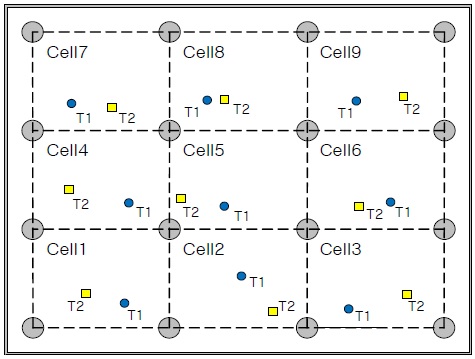
본 논문에서는 [13]와 다르게 TDOA기법에 의한 위치 추정을 다룬다. 선박의 실내 환경에서 단말기의 위치 추정 문제를 생각해보자. 일반적으로 선박은 여러개의 층으로 건조되어 있고 각 층은 두꺼운 철판으로 막혀있는 공간이 상대적으로 많다는 특징을 갖고 있다. 그림 1은 선박의 한 개 층에 대한 평면도를 보여주고 있는데 이러한 환경에서 위치를 추정하는 방법의 예를 보여주고 있다. 이 환경에서 단말기의 위치 추정은 매우 어려운 문제로 생각할 수 있다. 실제로는 각 층마다 평면상의 추정이 아닌 공간상의 추정 문제로 접근해야 한다. 그러나 공간상의 추정문제는 상대적으로 많은 계산량을 필요로 하기 때문에 평면상의 추정문제로 접근하는 것이 타당하다. 이는 선박내에서 단말기의 위치에 대한 의미가 정확히 어느 지점에 있는가가 아니라 어느 공간에 있는가가 중요하기 때문이다. 즉, 정확한 위치를 추정하기 보다는 어떤 단말이 몇 층의 어느 실에 있는가를 판별하는 것이 중요하기 때문이다.

[그림 1.] 선박내 구조 및 위치 추정에 대한 개념도

따라서, 본 논문에서는 GPS 신호가 도달하지 않는 선박내 공간에서 2차원 상의 위치 추정 문제를 다룬다. 이를 위해 먼저 TDOA 기법에 의한 위치 추정 방법에 대해 심도있게 살펴보고, 다음으로 선박의 환경에서 TDOA 기법을 적용 가능하도록 알고리즘을 제안한다. 마지막으로 세가지 관점에서 모의실험을 수행하여 선박의 실내 환경에서 TDOA기법에 의한 위치 추정의 타당성을 검증한다.

Ⅱ. 선박 환경에서 TDOA를 적용한 위치 추정 방법

2.1. TDOA 기법에 의한 위치 추정 방법

ISO/IEC JTC FDIS 24720 규격에 적용된 TDOA 위치 추정 방식은 단말기가 임의의 위치에 있을 때, 세 개 이상의 AP를 써서 단말기로부터 각 AP로 들어오는 신호의 도달시간을 측정하여 상호간 시간차를 구해 위치를 추정하는 방법이다. 위치 추정은 두 단계 과정으로 이루어지는데 첫 번째는 Estimation Process이고 두 번째는 Detection Process이다. Estimation Process는 세 개의 AP 중에서 임의의 하나를 기준으로 잡고 다른 두개의 AP와의 시간차를 알아냄으로서 단말기의 위치 추정값 를 구하는 것이다. 이는 미지수 x와 y를 구하는 문제로 x 혹은 y의 2차 방정식을 푸는 문제로 되기 때문에 결과적으로 추정값은 두 개의 값 과 로 나온다. 그런데 두 개의 추정값 중 하나는 구하고자 하는 추정값이고 다른 하나는 버려야 하는 값이다. 따라서, Detection Process에서는 두 개의 추정값인 과 중 단말기의 위치 (x, y)에 더 가까운 추정값 하나를 결정하는 것이다.

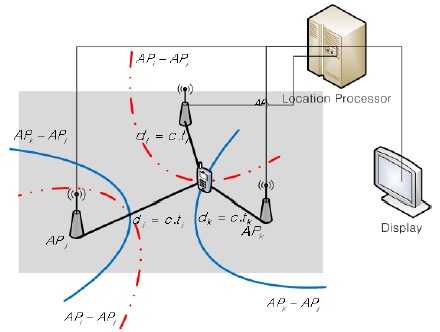
그러면 그림 2와 같이 단말기와 세 개의 AP가 동일한 평면상에 있을 때 단말기의 위치를 추정하는 문제를 생각해보자.

[그림 2.] 평면상에서 TDOA 추정 기법

단말기가 (x, y) 좌표에 있다고 가정하고 AP_i는 (x_i, y_i), AP_j는 (x_j, y_j), AP_k는 (x_k, y_k)에 위치하고 있다고 하자. 단말기로부터 송신된 신호가 AP_i에 도달하는 시간은 t_i이고, AP_j에 도달하는 시간은 t_j, AP_k에 도달하는 시간은 t_k인데 이는 세 개의 AP로부터 측정된다. 측정된 값 t_i, t_j, t_k로부터 단말기에서 각 AP까지의 거리를 구하면 (1)과 같이 된다.

여기서 c는 단말기에서 송신되는 RF 신호의 전파속도로 3 × 10⁸ m/sec이다. 그러면, 세 개의 AP 중에서 임의의 하나를 기준으로 하면, 즉, j째인 AP_j를 기준으로 하면, t_i와 t_j 간의 시간차인 dTOA_ij는 (2)와 같이 되고,

t_k와 t_j 간의 시간차인 dTOA_kj는 (3)과 같이 된다.

그러면 단말기에서 AP_i까지의 거리 d_i와 단말기에서 AP_j까지의 거리 d_j 간의 차는 |d_i – d_j|로 되는데 이를 δ_ij로 쓰면, δ_ij는 (4)와 같이 된다.

식 (4)의 양변을 제곱하여 추정하고자 하는 값인 x와 y로 정리하면 (5)와 같이 된다.

또한, 단말기에서 AP_k까지의 거리 d_k와 단말기에서 AP_j까지의 거리 d_j 간의 차는 |d_k – d_j|로 되는데 이를 δ_kj로 쓰면, δ_kj는 (6)와 같이 된다.

그러면 식 (6)의 양변을 제곱하여 x와 y로 정리하면 (7)와 같이 된다.

여기서 (5)의 좌변을 보다 간결하게 표현하기 위해 로 하면, (5)는 (8)과 같이 되고,

또한, 로 하여 (7)의 좌변을 정리하면 (9)와 같이 된다.

식 (8)과 (9)를 자세히 보면 x와 y의 연립방정식으로 되어 있음을 알 수 있는데 두 개의 식을 정리해 보면 (10)과 같이 될 수 있다.

그러면 (10)을 자세히 관찰해 보자. 이는 추정하고자 하는 두 개의 값인 x와 y의 1차방정식 꼴을 갖추고 있음을 알 수 있다. 식 (10)을 더 간결하게 표현하면 (11)과 같이 된다.

여기서, m과 b는 (12)와 같다.

이제 1차방정식 (11)를 이용하여 연립방정식 (8)과 (9)의 해를 구해보자. (11)을 (8)과 (9)에 각각 대입하여 두 식을 정리하면 (13)와 같은 x에 관한 2차방정식을 얻을 수 있다.

여기서 A, B, C는 (14)와 같다.

그러면 단말기의 위치 (x, y)의 추정값인 을 구하는 문제는 먼저 (13)에서 x에 관한 두 개의 근인 을 구하고, 다음으로 (11)에 를 대입하여 를 구하고 를 대입하여 를 구하는 것으로 된다.

지금까지의 과정을 다시 한번 요약하면, 평면상에서 단말기가 있는 임의의 위치 (x, y) 추정은 세 개 이상의 AP를 써서 추정할 수 있다. 그런데 TDOA 방식을 적용하여 추정할 경우에는 추정값이 두 개의 값 와 로 나온다는 것이다. 이는 두 개의 추정값 중 하나는 구하고자 하는 값이고 다른 하나는 버려야 할 값이라는 것이다. 따라서, 두 개의 값으로부터 구하고자 하는 값을 찾아야 하는 Detection Process가 이어져야 한다. Detection Process는 추정할 위치라고 가정하고 dTOA'_ij와 dTOA'_kj을 구해 실제로 AP_i, AP_j, AP_k에서 측정된 t_i, t_j, t_k로부터 dTOA_ij와 dTOA_kj를 구해 서로간의 오차를 계산하고, 같은 방법으로 를 추정 위치라고 가정하고 dTOA''_ij와 dTOA''_kj를 구해 dTOA_ij와 dTOA_kj 간의 오차를 계산하여 어떠한 경우가 더 적은 오차를 갖게 되는가를 알아내어 오차가 더 적은 추정값을 결정한다.

2.2. 선박의 환경에서 TDOA 기반 위치 추정 알고리즘

1절에서 세 개의 AP를 써서 TDOA 기법에 의한 평면상의 위치 (x, y)의 추정 문제를 알아보았다. 이 절에서는 선박이라는 환경에서 위치를 찾는 실제적인 문제를 고찰해 보자. 여객선을 포함한 대형선박은 일반적으로 여러개의 층으로 구성되어 있다. 이러한 환경에서 1절에서 쓴 평면상의 추정기법을 그대로 적용하기는 어렵다. 또한 공간상의 위치 (x, y, z) 추정기법이 있다고 해도 이를 그대로 적용하기는 어렵다. 이는 선박은 여러개의 층으로 구성되어 있기 때문에 높이에 대한 기준을 어디로 설정해야 하느냐가 어렵기 때문이다. 따라서, 본 논문에서는 여러 개의 층으로 구성되어 있는 선박에서 단말기가 어느 층에 있는지를 판정하고 난 다음에 단말기가 있는 층에서 단말기의 위치를 추정하는 문제를 다룬다.

선박은 그림 3과 같이 건조시부터 여러개의 층으로 구성되어 있기 때문에 각 층에서 단말기의 위치 추정은 그 층의 바닥이나 천정의 높이를 기준으로 추정문제를 다루는 것이 타당하다. 즉, 그림 3과 같이 여러개의 AP가 설치되어 있는 평면상의 추정문제로 생각해도 타당하다고 볼 수 있다.

[그림 3.] 선박의 각 층에서 위치추정에 대한 개념도

따라서, 선박의 실내 환경에서 단말기가 있는 위치를 추정하기 위한 알고리즘은 표 1과 같이 제안할 수 있다. 즉, Estimation Process에서는 단말기가 어느 층에 있는지를 결정하고 그 다음에 TDOA 기법을 써서 평면상의 위치를 추정하는 문제로 이루어진다. 또한, Detection Process는 두 개의 추정값 중 구해야할 추정값을 결정하는 것으로 이루어진다.

[표 1.] Estimation and Detection 과정

Estimation and Detection 과정

Ⅲ. 성능평가

선박의 실내 환경에서 TDOA를 적용한 위치 추정문제의 타당성을 검증하기 위해 세가지 관점에서 모의실험을 하였다. Example 1에서 단말기로부터 오는 신호의 전파시간를 측정하여, 측정된 값으로부터 거리를 환산하는 실험을 하였고, Example 2에서는 한 개의 단말기와 네 개의 AP를 써서 단말기의 위치 (x, y)를 추정하는 문제를 다루었다. 마지막으로 Example 3에서는 실제의 선박내 실내 환경과 비슷한 환경에서 16개의 AP를 써서 각 셀 당 2개의 시험 위치를 정해 이를 추정하는 실험을 하였다.

[Example1]

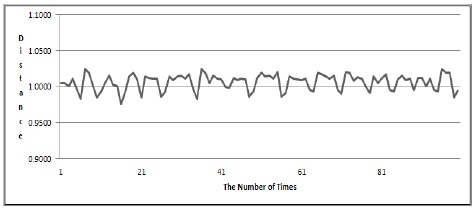
단말기로부터 AP까지의 거리를 1m, 3m로 두고 두 경우에 대해 신호의 전파시간을 측정하여 이를 거리로 환산하는 실험을 하였다. 먼저 1m 떨어진 경우에 단말기로부터 신호를 100회를 송신하여 각각의 전파시간 t₁, t₂, ⋯, t₁₀₀를 구하였고 이를 거리로 환산하여 d₁, d₂, ⋯, d₁₀₀을 구해 보았다. 그림 4는 결과값인 d₁, d₂, ⋯, d₁₀₀을 보여주고 있다. 실제로 매 실험마다 거리에 대한 오차가 발생하였는데 이를 통계적으로 분석한 결과, 평균은 1.006303m, 분산은 0.00012677m, 표준편차는 0.01131577m, 표준오차는 0.01125516m로 나타났다.

[그림 4.] 1m거리에서의 100회 측정 결과

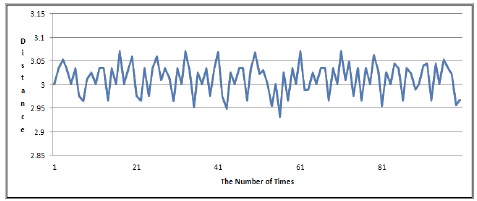
또한, 단말기와 AP간의 거리가 3m 떨어진 경우에 대해서도 100회의 실험을 하였는데 그림 5는 d₁, d₂, ⋯, d₁₀₀을 보여주고 있다. 이 경우에 평균은 3.013339m, 분산은 0.00109874m, 표준편차는 0.0333143m, 표준오차는 0.01919949m로 나타났다.

[그림 5.] 3m거리에서의 100회 측정결과

두 경우에 대한 실험을 통해 알 수 있었던 것은 거리가 길어질수록 거리 오차가 조금 더 커짐을 발견할 수 있었다.

[Example2]

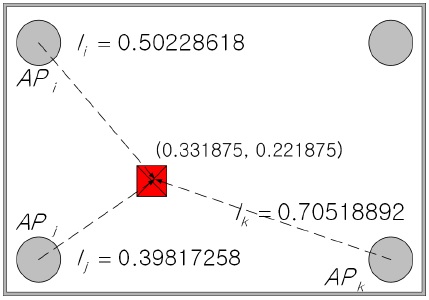
TDOA에 의한 평면상의 위치 추정 문제를 알아보기 위해 그림 6과 같이 한개의 단말기와 세개의 AP를 써서 단말의 위치 (x, y)를 추정하는 문제를 다루었다. 먼저 단말기를 (x, y) = (0.331875, 0.221875) 위치에 두고 네 개의 AP에서 신호를 받아 전파시간이 짧은 세 개의 AP를 결정하였다. 그리고 세 개의 AP에서 측정된 t_i, t_j, t_k로부터 단말에서 각 AP까지의 거리를 환산하면 은 0.50846737m, 는 0.40275322m, 는 0.69531299m로 나타났다. AP_j를 기준으로 하여 다른 두 AP_i와 AP_k와의 dTOA_ij, dTOA_kj를 구하였다. 그런 다음 TDOA를 수행하여 = (0.32829723, 0.22471678)를 찾았다. 추정결과를 분석해보면 x방향의 추정오차는 이었고 y방향으로의 추정오차는 |y – ŷ|=-0.0028418m으로 나타났다.

[그림 6.] 네 개의 AP를 쓴 TDOA 위치 추정 문제

[Example3]

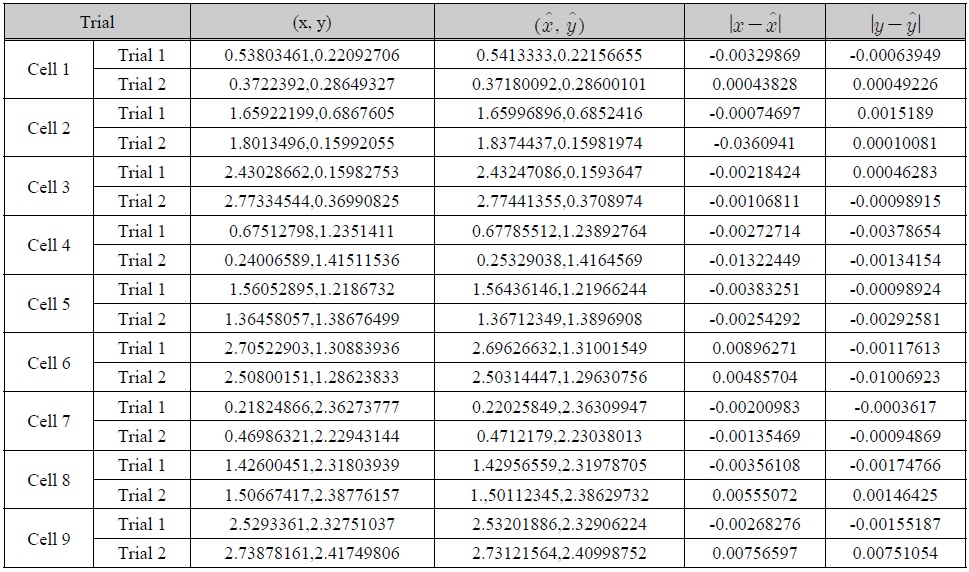
선박의 실내 환경에서 단말기가 위치하고 있는 층의 AP 배치 상태는 그림 7과 같다고 보자. 즉, 16개의 AP가 직교 배열로 설치되어 있는 상황에서 9개의 셀이 나온다. 각 셀에서 2회의 추정 실험을 하였는데 표 2는 그에 대한 추정결과를 보여준다.

[그림 7.] 16개의 AP를 직교 배열로 쓴 TDOA 위치 추정 문제

[표 2.] 18번의 위치 추정에 대한 측정값과 오차

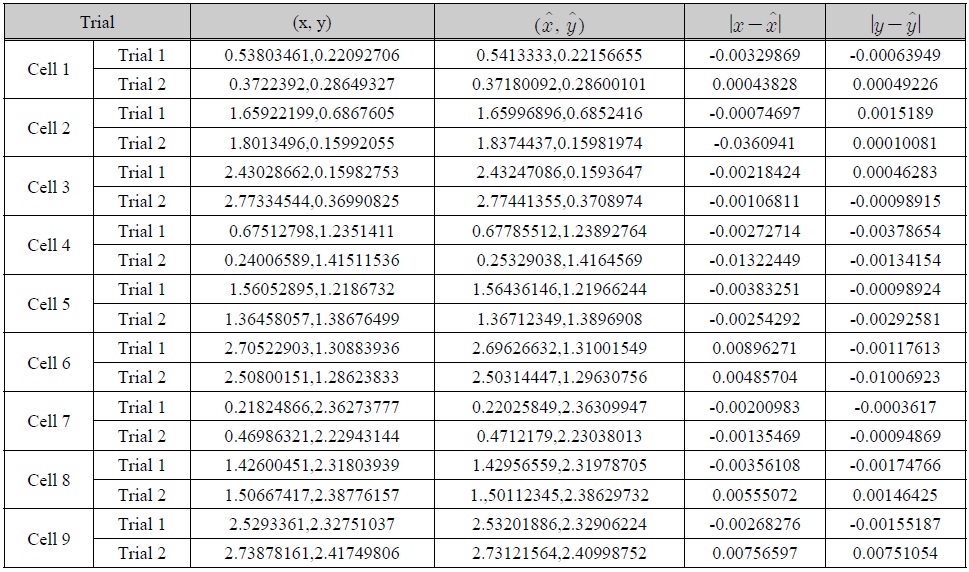
18번의 위치 추정에 대한 측정값과 오차

18회의 모의실험을 통해 결과를 분석해보면, x방향으로의 추정값에 대한 기대값은 로 나타났고 분산은 Var(x)=0.000089654793519m으로 나타났다. 또한, y방향으로의 추정값에 대한 기대값은 이었고 분산은 Var(y)=0.000010288533277m으로 나타났다.

Ⅳ. 결 론

본 논문에서는 여러개의 층으로 구성되어 있는 선박의 실내 환경에서 TDOA기법을 적용하여 위치를 추정하는 문제를 다루었다. 먼저 단말기가 있는 층을 결정하는 방법으로는 선박의 중앙 부위에 별도의 AP을 층마다 두고 단말에서 AP로 들어오는 신호의 강도를 비교하여 단말기가 있는 층을 결정하는 방법을 생각하였다. 다음으로는 단말기가 있는 층에서 단말기의 위치를 TDOA 기법을 써서 추정 문제를 다루었다. Example 1에서 단말기로부터 AP로의 전파시간을 측정하여 단말기와 AP간의 거리를 구하는 실험을 1m, 3m인 환경에서 모의실험 하였다. 1m, 3m 경우에 대해 100회의 실험을 수행한 결과 측정 오차는 거리가 커짐에 따라 좀 더 크게 나타남을 알았다. 그러나 각각의 실험에 대해 기대값과 분산을 구해서 분석한 결과 전파시간 측정에 의해 거리를 환산하는 방법이 타당성이 있다는 사실을 알게 되었다. 다음으로 Example 2에서는 네 개의 AP를 써서 단말기로부터 오는 신호의 전파시간이 가장 짧은 세 개의 AP를 선택하고 선택된 세 개의 AP를 써서 단말기의 위치 (x, y)를 추정하는 문제를 다루었다. 실제로 단말기를 (x, y) = (1.331875, 1.221875)인 지점에 두고 TDOA 기법을 써서 모의실험을 하였는데 추정결과는 = (1.32829723, 1.22471678)으로 나타나 추정 성능이 아주 우수함을 알 수 있었다.

마지막으로 Example 3에서는 16개의 AP가 설치되어 있는 공간에서 각 셀에서 2번씩 모의실험을 하여 추정오차를 구해보았다. 18번의 실험을 수행한 결과 위치 추정 오차가 상당히 작음을 알 수 있었다. 본 연구는 선박이라는 환경에서 각 층의 위치 추정을 평면상의 추정 문제로 가정하고 다루었는데 실제로 선박의 각 층은 공간적 접근을 해야 한다. 따라서 향후 연구는 3차원 공간에서 위치 추정에 관한 문제를 다루어져야 한다고 생각한다.

참고문헌

1. Lee J. J., Kwon J. W., Jung M. A, Lee S. R. 2010 “Fingerprinting Bayesian Algorithm for Indoor Location Determination,” [The Journal of Korea Information and Communications Society] Vol.35 P.888-894
2. Lee J. J., Jung M. A, Lee S. R., Song I. H. 2011 “KNN/ANN Hybrid Location Determination Algorithm for Indoor Location Base Service,” [The Journal of Institute Of Electronics And Information Engineers] Vol.48 P.109-115
3. Lee J. J., Song L. H., Kim J. H., Lee S. R. 2011 “Optimized KNN/IFCM Algorithm for Efficient Indoor Location,” [The Journal of Institute Of Electronics And Information Engineers] Vol.48 P.125-133
4. Lee J. J., Jung M. A, Lee S. R. 2010 “KNN/PFCM Hybrid Algorithm for Indoor Location Determination in WLAN,” [The Journal of Institute Of Electronics And Information Engineers] Vol.47 P.146-153
5. Jo H. G., Jeong S. Y., Kang S. J. 2012 “Enhanced Accurate Indoor Localization System Using RSSI Fingerprint Overlapping Method in Sensor Network,” [The Journal of Korea Information and Communications Society] Vol.37C P.731-740
6. Kim T., Tak S. 2013 “Modeling and Performance Evaluation of AP Deployment Schemes for Indoor Location-Awareness,” [Journal of the Korea Institute of Information and Communication Engineering] Vol.17 P.847-856
7. Cha J. Y., Kong Y. B., Choi J. W., Ko J. H., Kwon Y. G. 2012 "IEEE 802.15.4a based Localization Algorithm for Location Accuracy Enhancement in the NLOS Environment," [Journal of the Korea Institute of Information and Communication Engineering] Vol.16 P.1789-1798
8. Son S., Choi H., Cho H., Baek Y. 2013 "Location Information Reliability-Based Precision Locating System Using NLOS Condition Estimation," [The Journal of Korea Information and Communications Society] Vol.38C P.97-108
9. Wooo S., Jeon H., Park H. 2006 “A Study on NLOS Error Solution Method in Indoor Location Estimate,” [Korea Computer Congress] Vol.33 P.178-180
10. Lim Y., Park J., Ahn S. 2008 “A Geometric Approach for the Indoor Localization System,” [Journal of The Institue of Electronics Engineers] Vol.45 P.1058-1065
11. Ahn D., Ha R. “Indoor Localization Methodology Based on Smart Phone in Home Environment,” [The Journal of Korea Information and Communications Society '14-04] Vol.39C P.315-325
12. Cong L., Zhuang W. 2001 “Non-line-of-sight error mitigation in TDOA mobile location,” [IEEE Global Telecommunications Conference] P.680-684
13. Kim B., Jeong M. A., Lee S. R. 2014 “Location Estimation Method Employing Fingerprinting Scheme based on K-Nearest Neighbor Algorithm under WLAN Environment of Ship,” [Journal of the Korea Institute of Information and Communication Engineering] Vol.18 P.2530-2536