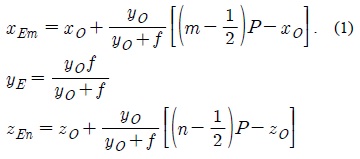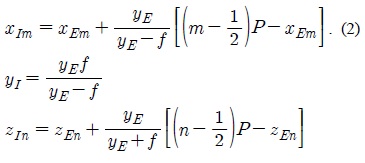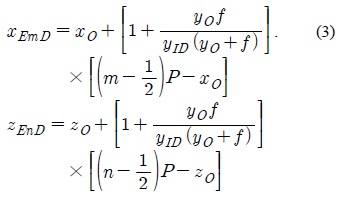집적영상 (Integral Imaging)은 1908년 Lippmann에 의해 처음 제안된 3차원 영상 구현 방법이다[1]. 집적영상은 자연광의 이용이 가능하고 완전한 색상 구현, 시야각 내에서 연속적인 관찰시점과 Autosteroscopic 영상 제공, 무안경 방식 그리고 시차영상의 획득과 재생과정이 다른 3차원 영상 기술에 비하여 상대적으로 간편하다는 장점이 있다[2-7].

집적영상은 3차원물체를 다양한 시점에서 관찰하였을 때의 정보를 획득하고, 이를 재생함으로 3차원 물체와 동일한 영상을 재생하는 영상구현방법이다. 물체의 다양한 시점에 대한 정보를 획득하기 위하여 요소렌즈(elemental lens)가 연속적으로 배열된 평면 형태의 렌즈배열(lens array)을 이용한다. 이 때 렌즈배열 내에 위치한 요소렌즈의 위치에 대응하여 3차원 물체의 연속적인 시차정보가 결상된다. 이 시차정보의 배열을 요소 영상이라 하며, 요소영상은 카메라 등의 픽업장치를 이용하여 획득된다. 3차원 영상 재생은 렌즈배열을 영상 표시장치 앞에 놓음으로 요소영상 획득시 3차원 물체가 놓였던 깊이에 3차원 영상을 재생한다. 집적영상의 재생영상에서 관찰되는 특성으로써 재생영상이 반전된 깊이 감을 갖는 도치영상 (Pseudoscopic image) 문제가 있다. 재생상의 도치영상 문제를 해결하기 위한 초기의 연구로는 요소영상 획득시 사용되는 광학계를 GRIN (gradient index)렌즈 어레이[8,9], 오목렌즈 어레이, 그리고 렌즈어레이를 한 번 더 사용하는 방법 [10], 등이 연구 되어졌다. 그러나 위 방법들은 재생상이 허상으로만 구현될 수 있는 한계가 있다. 정치 실상 구현을 위한 연구로는 광학적인 방법을 이용한 다양한 깊이 변환법이 시도 된바있다[11-14]. 그러나 특별한 광학장치를 부가적으로 활용하여 재생되는 정치실상 (Orthoscopic real image) 즉, 바른 순서의 깊이를 갖는 영상은 재생영상의 왜곡과 질적 저하를 수반 한다.

본 논문에서는 물체와 요소영상 그리고 재생상의 기하학적 관계를 정의하고 이들의 관계에 대한 분석을 통하여 광학적 손실과 부가적인 수차 없이 도치영상문제를 해결하고자 한다. 요소영상과 획득계 그리고 재생계의 분석을 통하여 수식을 유도 하였으며 이를 이용하여 재생하고자 하는 깊이에 대응하도록 요소영상 변환이 가능하다. 제안하는 방법의 유용성을 보이기 위하여 이론적 분석과 실험을 수행하였다.

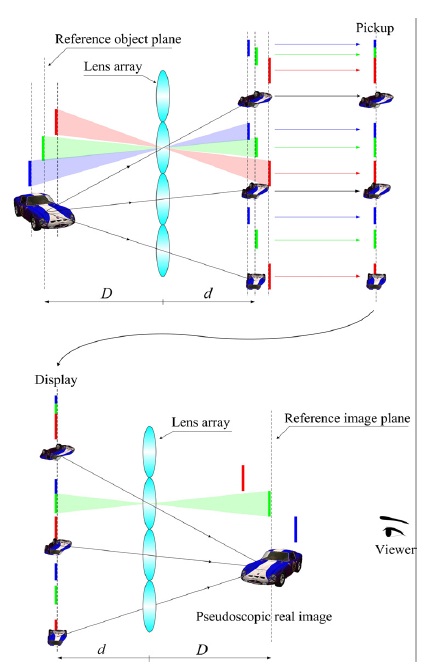
일반적인 집적영상법 (Integral Imaging Method)을 통해서 재생되는 영상은 도치실상(Pseudoscopic real image)의 형태로 관찰된다. 이는 광학계의 문제로 인하여 발생하는 것이 아니며 3차원 물체의 정보가 획득되며 재생되는 과정에서 나타나는 자연스러운 결과이다.

그림 1은 이를 표현한 것으로 요소영상 획득시 3차원 물체와 렌즈배열 사이의 깊이 순서는 재생과정에서 동일한 순서를 가진 영상으로 재생되기 때문이다. 도치영상 (Pseudoscopic image)은 반전된 깊이로 재생되므로 3차원 영상으로 관찰자에게 제공하기에는 부적절 하며, 도치영상 문제는 집적영상이 상업적으로 성공하기 위해서 해결 돼야할 과제이다.

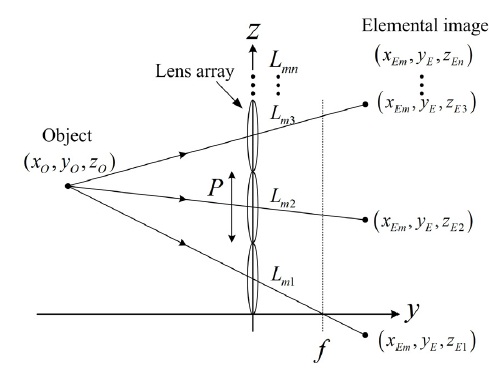
집적영상 (Integral Imaging) 에서 물체의 3차원 정보는 요소렌즈(elemental lens)가 연속적으로 배열된 렌즈배열(lens array)을 통하여 결상되며 카메라나 CCD(Charge Coupled Device)등의 장비를 이용하여 2차원 형태로 저장된다. 저장된 2차원 영상을 요소영상배열(elemental image array)이라 하고 각 요소렌즈에 대응되는 영상을 요소영상(elemental image)이라 하며 획득과정은 그림 2와 같이 표현 할 수 있다. 그림 1은 공간상의 점 물체, 렌즈배열, 요소영상의 기하 광학적 관계를 2차원 좌표계로 나타낸 것이다.

이때 변수들의 대응관계는 다음과 같이 표현된다.

그림 2와 식 (1)에서 좌표의 원점은 렌즈배열의 제일 아래에 위치한 요소렌즈의 가장자리이다. (x_O,y_O,z_O)는 물체의 좌표이며, 실물체의 경우 y_O < 0을 만족한다. P는 이웃한 요소렌즈광축 사이의 거리이고, 요소렌즈의 직경이기도 하다. f는 요소렌즈의 초점거리 이며, x_Em과 z_En은 각각 m과 n번째 요소렌즈에 의한 x축과 z축 방향의 결상 점을 나타낸다. y_E는 요소영상의 결상 깊이이며, L_mn은 렌즈배열 내에서 각 요소렌즈의 위치를 나타낸다.

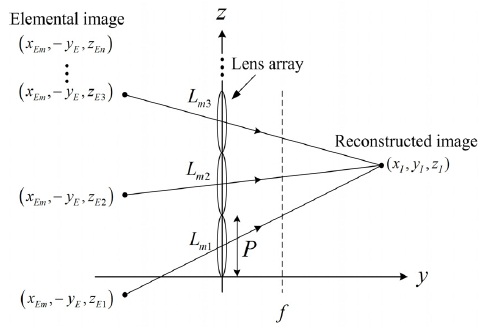
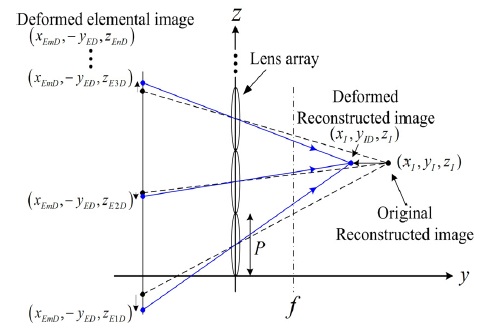
재생상의 깊이 변환은 획득된 요소영상배열의 위치에 대응하는 재생영상 (Reconstructed image)의 위치관계를 참고하여 수행되어야 한다. 따라서 각 요소영상의 위치와 이에 대응하는 재생영상의 기하학적 관계에 대한 분석이 필요하며, 그림 3은 이를 표현한 것이다.

요소영상과 재생영상들 사이의 변수들의 대응관계는 다음과 같이 표현된다.

그림 3과 식 (2)에서 (x_I,y_I,z_I)는 재생영상의 좌표이고, 다른 변수들은 그림 2의 설명과 동일하다.

그림 4는 재생영상의 깊이를 변환하기 위한 요소영상의 좌표변환을 설명하기 위한 것으로 변환되기 전 요소영상의 좌표는 (x_Em, -y_E, z_En)이고 이 점들에 대응되는 재생영상의 집적점 (integrated point)의 좌표는 (x_I,y_I,z_I)으로 그림에서는 점선으로 표시된 부분이다. 재생영상을 임의의 깊이 (x_I,y_ID,z_I)에 집적하기 위하여 그림에서 표현한 것처럼 대응되는 요소영상의 변환이 필요하며 변환된 점의 좌표는 (x_EmD, -y_E, z_EnD)로 그림에서 실선으로 표현하였다.

변수를 정하는 과정에서 요소영상면과 렌즈배열사이의 거리를 변환 전과 후 모두 -y_E이다. 그림 4에 표현된 것처럼 깊이가 변환된 재생영상 (Defromed recostructed image)의 좌표는 변환되기 전 재생영상(Original reconstructed image)과 y 축 좌표에서만 차이를 보인다. 그러나 요소영상면에서는 변환된 재생영상에 대응되는 x 축과 z 축좌표에 대한 좌표변환이 필요하다. 변환하고자 하는 깊이 y_ID 를 결정하였을 경우 이에 대응되는 요소영상면위의 점들은 식 (1)과 (2)를 응용하여 유도할 수 있고 요소영상면 y = y_E (y_E > 0) 이므로 변환된 좌표는 다음과 같다.

식 (3)은 변환되기 전 요소영상의 좌표 x_Em 과 z_En을 포함하고 있지 않으며 y_ID 를 임의의 값으로 주었을 경우와 물체의 위치와의 관계를 나타내고 있다. 이 수식이 의미하는 바는 알고 있는 물체 정보에 대하여 재생영상을 위치시키고자 하는 깊이에 재생하기 위한 중간과정인 요소영상획득 과정 없이 원하는 깊이에 집적될 요소영상을 얻을 수 있음을 말한다.

획득된 요소영상에서 재생상의 깊이를 변환하고자 하는 경우 수식 (1)을 x_O 와 z_O 에 대하여 정리한 후 수식 (3)에 각각 대입하면 되며 그 결과는 식 (4)와 같다.

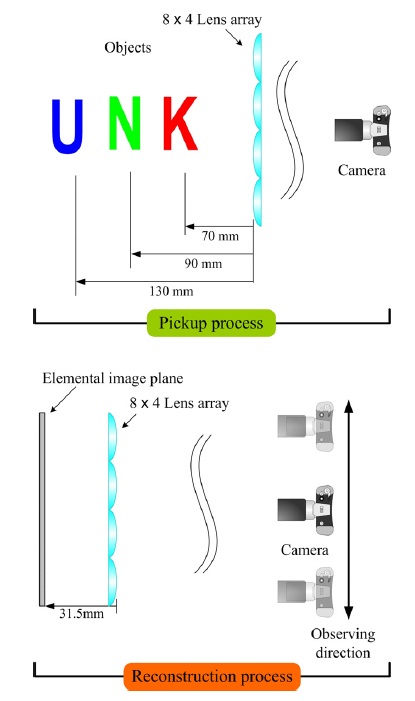
제안하는 깊이변환법에 대한 구현 가능성을 확인하기 위하여 깊이변환 실험을 수행하였다. 각 재생상의 특성을 확인하기 위하여 원본 요소영상으로 재생된 상과 제안하는 변환법을 이용하여 변환된 요소영상의 재생 상을 비교하였다. 그림 5는 요소영상 획득과 재생과정의 실험 셋업 이다. 실험에서 요소렌즈의 직경은 10mm이고 초점거리는 30 mm이며 요소렌즈는 사각형 형태의 평볼록렌즈이고 렌즈배열 전체크기는 8X4이다.

물체는 K, N, U 알파벳 문자가 사용 되었으며 각각 렌즈배열로부터 거리 70mm, 90mm, 110mm 떨어져 있다. 요소영상 재생과정에서는 요소영상을 획득할 때와 동일한 사양의 렌즈배열을 사용하였다. 또한 렌즈배열은 요소영상배열로부터 31.5 mm에 위치시켰다. 재생영상의 특성을 확인하기 위하여 카메라를 수평방향으로 이동하며 관찰하였다.

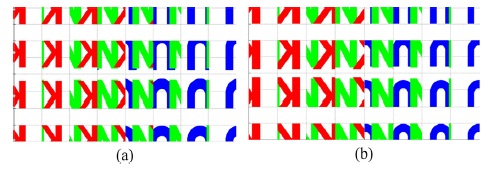
그림 6(a), (b)는 각각 획득된 원본 요소영상과 깊이가 변환된 요소영상이다. 그림 6(b)의 요소영상은 원본 요소영상으로부터 제안하는 깊이변환법을 이용하여 변환한 결과이다.

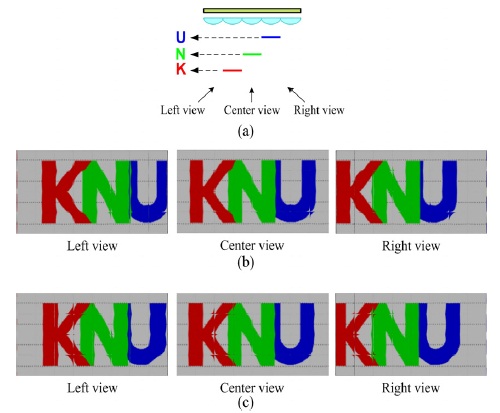
그림 7(b)와 (c)는 각각 그림 6(a)와 (b)의 요소영상을 이용하여 재생한 결과이다. 그림 7(b)는 도치실상으로 재생되었다. 도치실상은 반전된 깊이로 재생되는 특성이 있는데 이로 인하여 관찰위치에 기대되는 재생영상이 관찰되지 않는 것이다. 이를 구체적으로 설명하기 위하여 그림 7(a)의 관찰위치와 그림 7(b)에서 재생된 영상을 논의하면, 관찰 위치가 왼쪽일 경우 관찰자는 물체의 왼쪽에 대응하는 영상이 관찰될 것을 기대한다. 그러나 그림 7(b)의 재생영상을 보면 왼쪽에서 관찰할 때 물체의 오른쪽 부분이 관찰되며, 오른쪽에서 관찰할 때 물체의 왼쪽 부분이 관찰되는 것을 확인할 수 있다.

그림 7(c)는 제안하는 깊이변환법을 이용하여 깊이가 변환된 그림 6(b)의 요소영상을 이용하여 재생된 결과로써 정치실상으로 재생되었다. 도치영상과 달리정치실상은 올바른 깊이를 갖는다. 이는 다양한 관찰 위치에서 관찰한 재생상을 통하여 확인 할 수 있는 특성이다. 그림 7(a)의 관찰 위치와 이에 대응하는 영상을 그림 7(b)의 정치실상으로 재생된 결과에서 살펴보면, 관찰 위치에 대응하여 올바른 영상이 재생됨을 확인 할 수 있다. 이는 제안하는 도치영상에서 정치실상으로의 깊이변환법 이론을 실험으로 검증한 결과라 할 수 있다.

결론적으로 본 논문에서는 집적 영상 기술에서 재생상의 도치영상문제를 해결하기 위하여 요소영상의 좌표를 재생깊이를 고려하여 변환하는 새로운 깊이변환법을 제안하였으며 기하학적 분석을 통하여 제안하는 변환법을 제시하였다. 또한 제안하는 방법의 유용성을 확인하기 위하여 획득된 요소영상을 이용하여 도치실상 재생 실험과, 요소영상변환을 통하여 정치실상 재생실험을 수행하여 재생된 영상들을 관찰위치와 비교하였다. 실험결과 깊이가 반전되는 특성을 갖는 도치영상이 변환된 후 올바른 깊이 감을 갖는 정치실상으로 재생됨을 확인하였다.