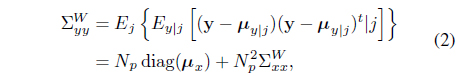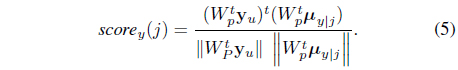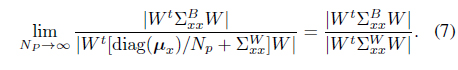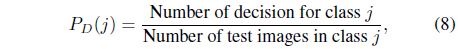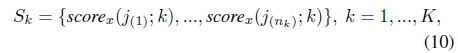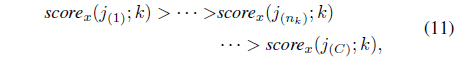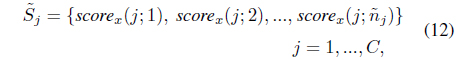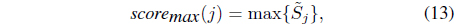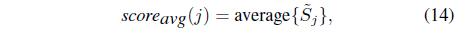Face classification has many applications in security monitoring and intelligent surveillance, as well as robot vision, image and video retrieval, and human-machine interfaces [1-3]. However, it is challenging to classify a facial image acquired in an uncontrolled setting, such as those captured at long distances. Unexpected blurring and noise may occur, in addition to conventional distortions caused by pose, illumination, and expression changes. To address these issues, various classifiers have been developed based on statistical analysis, including Fisher linear discriminant analysis (LDA) combined with principal component analysis (PCA) [4], (often referred to as “Fisherfaces”), as well as the “Eigenfaces” method, which uses only PCA [1]. Typically, the number of training images is much less than the number of pixels. Thus, the Fisher LDA requires a dimensionality reduction such as PCA in order to avoid the singularity problem, often referred to as the “small sample size problem.” However, photoncounting (PC) LDA does not suffer the singularity problem associated with a small sample size [5]. Originally, PC-LDA had been developed to train grayscale images and classify a photonlimited image obtained under low illumination. However, it has been shown that PC-LDA is also suitable for classifying grayscale images, which can be obtained by a visible camera [6].
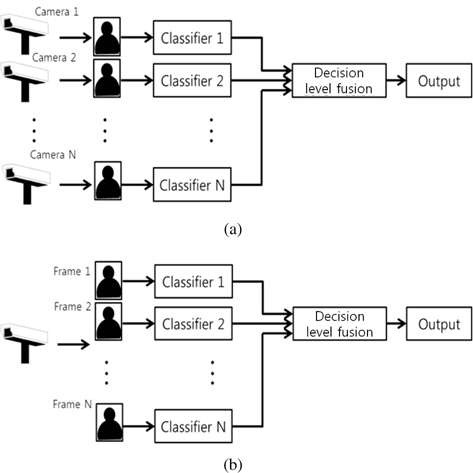
Decision-level fusion is a high-level data fusion technique [7, 8]. It aims to increase classification accuracy by combining multiple outputs from multiple data sets. Compared to single frames, multi-frames contain additional information acquired from varying spatial or temporal settings, as illustrated in Figure 1. Various fusion rules such as maximum, averaging, and majority-voting rules have been studied in the literature [9, 10]. Bayesian estimation and Dempster-Shafer evidential reasoning are often adopted for decision-level fusion [11]. In [12], preliminary results are provided for multi-frame recognition with several data sets.
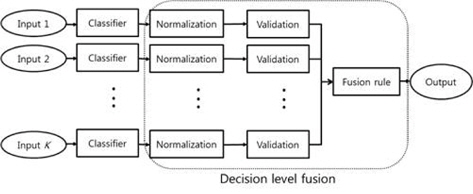
In this paper, multi-frame decision-level fusion with PC-LDA is discussed. Decision-level fusion involves three stages: score normalization, score validation, and score combination. After the scores are normalized, candidate scores are selected using a screening process (score validation). Subsequently, the scores representing the classes are combined to render a final decision using a fusion rule (score combination). The validation stage screens out “bad” scores that can degrade classification performance. The maximum, averaging, and majority voting fusion rules are investigated in the experiments. Three facial image datasets (ORL, AR, Yale) [13-15] are employed to verify the effectiveness of the proposed decision-level fusion scheme.
The remainder of the paper is organized as follows. PC-LDA is discussed in Section 2. Section 3 describes decision-level fusion. The experimental results are presented in Section 4. The conclusion follows in Section 5.
This section briefly describes PC-LDA. PC-LDA realizes the Fisher criterion using the Poisson distribution, which characterizes the semi-classical photo-detection model [16]. A PC vector y is a random feature vector corresponding to a normalized image vector x. Thus, the dimensions of x and y are the same value, which is the number of pixels
The between-class covariance measures the separation of classes as
where the class-conditional mean and the mean vectors are derived as
where diag(·) denotes a diagonal matrix. Thus, the following Fisher criterion can be derived:
where the column vectors of
The class decision can be made by maximizing a score function, as follows:
where
The photo-counting vector y
The mean-squared (MS) error is the same as the variance of
Two performance measures are calculated to evaluate the performance of the classifiers. One is the probability of correct decisions (
Decision-level fusion is composed of three stages: score normalization, validation, and fusion rule processes; these are illustrated in Figure 2. The scores must be normalized if they are presented in different metric forms. The candidate scores are selected during the validation process. Finally, they are combined to create a new score, using a fusion rule. For the score validation, a score set S
where
where is the number of scores for class
where Eqs. (13)-(15) represent maximum, averaging, and majority voting rules, respectively.
4. Experimental and Simulation Results
This section describes two types of experiments. The first involves the verification of PC-LDA with a single frame. In the second experiment, decision-level fusion is tested with artificially degraded test images.
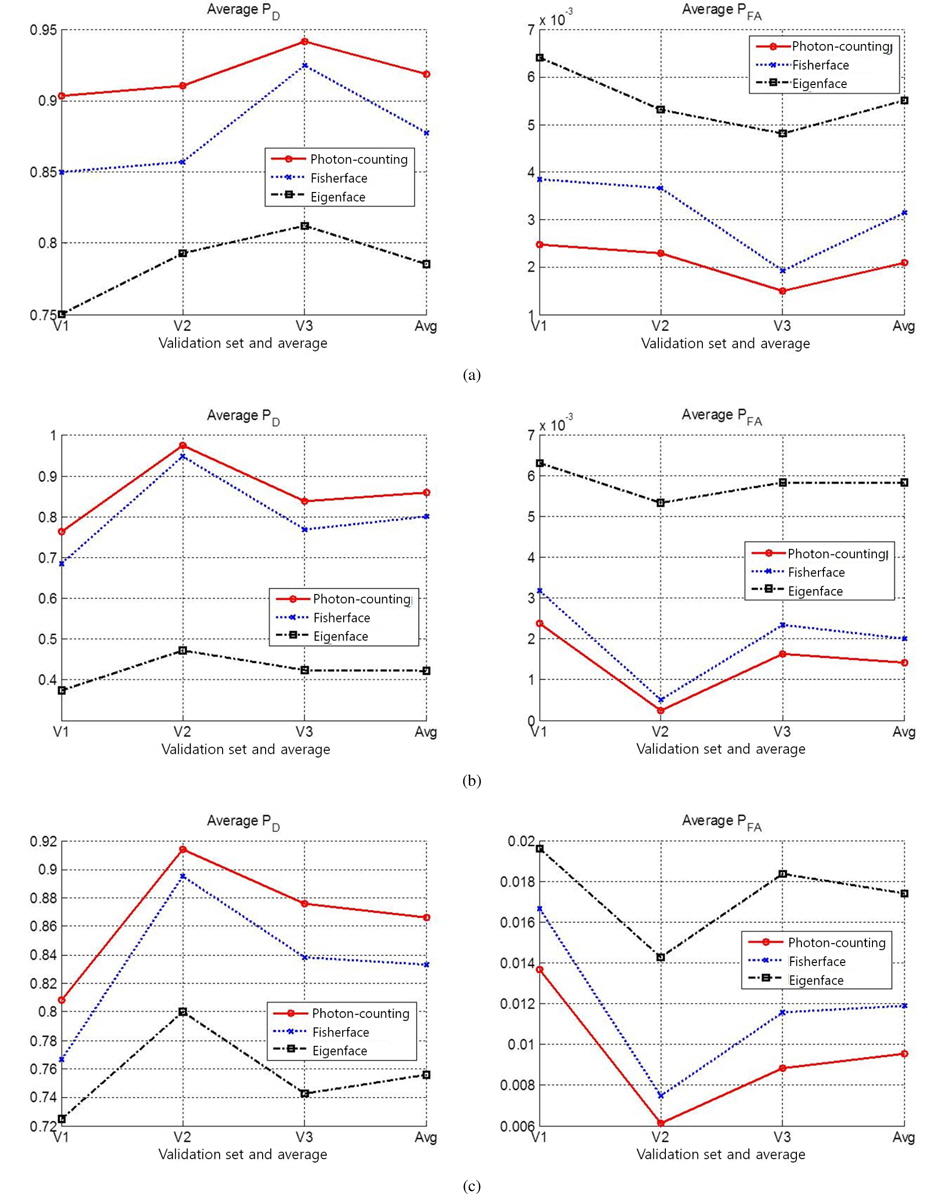
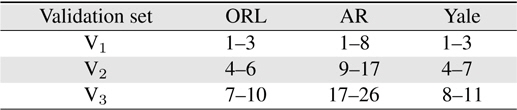
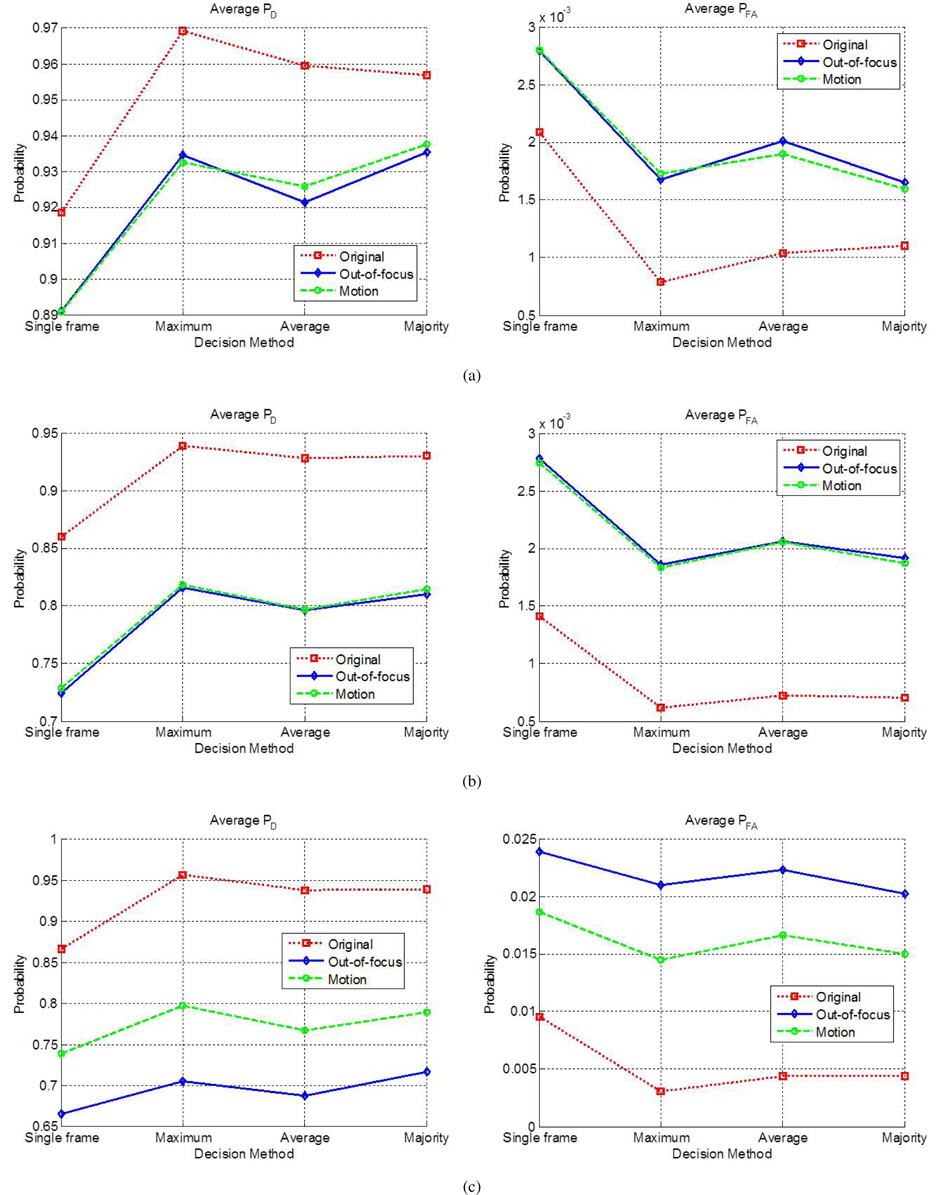
Three facial image datasets were used for the performance evaluation: ORL [13], AR, [14], and Yale [1]. The MATLAB format was utilized for the Yale database [15]. Figure 3 shows the sample images of five classes from three datasets. The datasets contain 40, 100, and 15 classes, respectively; these classes respectively contain 10, 26, and 11 images. The dataset image sizes are 92 × 112, 120 × 165, and 64 × 64 pixels, respectively. Each database was divided into three validation sets, as shown in Table 1. For the single-frame experiment, each validation set was trained and all other validation sets were tested. For example, when three images (image indexes 1–3) in set V1 of the ORL dataset were trained, the other seven images (image indexes 4–10) were tested. Figures 4 represents the five column vectors of the PC-LDA face, Fisherface, and Eigenface projection matrices, respectively, in the image scale; three images from set V1 of the ORL dataset were trained to produce these results. As illustrated in the figures, the PC-LDA face presents the optimal structural diversity among the three classifiers, although the Eigen face method is more dependent on the intensity distribution, compared to the other methods. Figure 5 shows the average probability of detection (
[Table 1.] Image index in validation sets
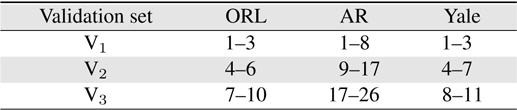
Image index in validation sets
For the decision-level fusion experiment, test images were blurred by out-of-focus and motion blurring point-spread functions, to simulate long-distance acquisitions. Out-of-focus images were rendered by applying circular averaging with an 8 pixel radius. Heavy motion blurring was rendered by a filter approximating the linear motion of a camera for a distance of 20 pixels, with an angle of 45◦ in a counter-clockwise direction [6]. Figure 6 shows the sample test images from ORL after blur rendering.
It was assumed that one pair of test images in the validation set was obtained by multiple sensors; thus, the total number of frames (K) was set to two. For example, if the number of test images was seven in the single-frame experiment, the number of test pairs for the multi-frame fusion was 21 (= 7
This study investigated the effectiveness of a decision-level fusion system with multi-frame facial images. Three decision-level fusion schemes were investigated, following the score normalization and validation processes. Two types of blurring point-spread functions were applied to the test images, in order to simulate harsh conditions. The results indicated that the proposed data fusion scheme improved the classification performance significantly.