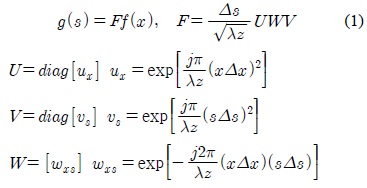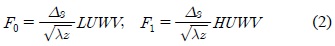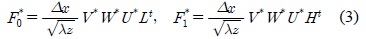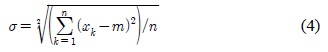In this paper, we propose a new subband quantizer which is a type of quad-tree for applying to digital hologram compression based on Fresenelet transform. After executing Fresnelet transform to the captured digital holgoram, we analyze effect of the designed quantizer for the reconstructed objects from analyzing average energy of each coefficient and visual importance in all subbands. We analyze distribution of coefficient and set dynamic range for each subband, and then design subband quantizer. For enhancing effectiveness of the designed quantize, we adopt a method using the coefficients which are located out of dynamic range, which are named by exception indices. From this, we can obtain more effective quantizer which has higher performance in a range of σ′ = 5.0.
최근 3D의 발전으로 3D 콘텐츠 및 제품이 개발되고 있다. 따라서 다음 세대의 3D기술 중 완벽한 3D디스플레이인 디지털 홀로그래피에 대하여 많은 연구자 및 정부 관계자들이 지목하고 있다. 하지만 대부분의 연구는 광학 홀로그램의 획득과, 이를 효과적으로 복원하는 기술들에만 국한되어 있었다[1]. 광학 홀로그램은 획득과 전송 등의 많은 문제점 때문에 CCD(Charge Coupled Device) 카메라로 영상을 획득하거나 컴퓨터에 의해 간섭패턴을 계산하는 컴퓨터 생성 홀로그램(Computer Generated Hologram, CGH)이 개발 되었다. 디지털 홀로그램(Digital Hologram, DH)과 연관된 영역에서 데이터의 크기는 중요한 이슈 중 하나이다. 따라서 디지털 홀로그램에 대한 데이터 압축 방법은 중요한 연구 분야가 되었다.
Yoshikawa[2,3]는 홀로그램의 정보량을 줄이는 방법으로 영상을 재구성 했을 때의 해상도가 HVS에 비해 너무 크다는 단점을 개선하여 해상도를 줄이는 방법과 보간법으로 홀로그래픽 3D 디스플레이의 정보량을 줄이는 방법을 제안하였다. 또한 JPEG(Joint Photographic Experts Group)과 같은 정지영상의 압축 표준 기술을 이용한 프린지 패턴이 일반적인 2차원 영상과는 많이 다르므로 큰 효과를 얻지는 못하였다[4,5]. 이를 해결하기 위해 프린지를 몇 개의 세그먼트로 나누어 DCT(Discrete Cosine Transform)를 수행하고, 동영상 압축 표준인 MPEG-1[6]과 MPEG-2[7]로 압축하였다. Javidi 교수의 연구팀은 홀로그램을 새로운 비-균일 양자화기를 이용하여 양자화를 하고, Lempel-Ziv(LZ77, LZW)[8,9], Huffman[10], Burrows-Wheeler(BW)[11]과 같은 무손실 부호를 이용하여 데이터를 압축하였다[12]. 본 연구팀에서는 홀로그램을 주파수 변환(DCT)하여, 주파수 영역에서의 잔여영상 생성기법을 적용하여 데이터 압축을 수행한다[13].
본 논문에서는 홀로그램 영상[14]에 대해 프레넬릿 변환(Fresnelet Transform, FNLT)을 이용하여 주파수 영역에서 각각의 부대역(subband)의 특성을 분석한다. 이러한 분석 정보를 바탕으로 부대역에 따른 우선 순위를 정하고 부대역에 따른 양자화 방식을 제안한다. 또한 양자화 효율을 높이기 위해 예외 계수를 도입하는 방법을 제안하였다. 본 논문은 다음과 같이 구성된다. 2장에서는프레넬릿 변환에 대해서 설명하고, 3장에서는 양자화기 설계 방법을 제안하다. 4장에서는 실험한 결과를 보이고, 5장에서 결론을 맺는다.
프레넬 변환은 식 (1)과 같이 입력으로부터 거리
홀로그램은 일반적인 2차원 영상과 달리 객체의 모든 광원의 정보를 가지고 있어 2차원 영상에 적용되는 영상처리 방법을 적용하기 어렵다. 그림 1은 식 (1)을 이용하여 2차원 형태로 홀로그램에 적용한 것으로 그림 1(a)는 홀로그램을 생성할 객체 영상이고 그림 1(b)는 홀로그램, 그림 1(c)는 프레넬 변환을 적용한 영상이다. 그림 1(b)를 통해 홀로그램은 많은 고주파 성분을 가지고 있다는 것을 확인 할 수 있다.
식 (1)의 프레넬 변환 필터
식 (2)로부터 유도되는 실수부와 허수부는 그림 2(a) 및 (b)와 같이 고주파 성분이 남아 있는 것을 확인할 수 있고, 또한 각 부대역에 에너지 분포가 거의 동일한 것을 확인할 수 있다.
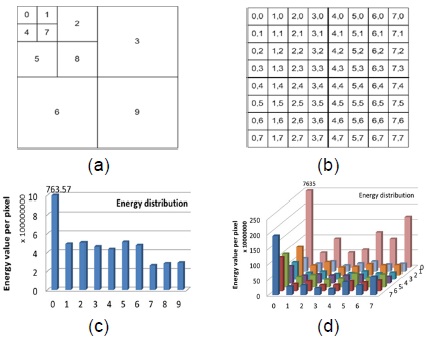
반면 프레넬릿 결과를 크기(그림 2(c))와 위상(그림 2(d))의 형태인 복소항으로 바꾸면 그림 3과 같은 특성을 나타낸다는 것을 확인할 수 있다. 그림 3은 프레넬릿 부대역들의 화소당 평균 에너지에 대한 분포를 분석하여 나타내었다. 사용된 평균 에너지는 그림 2(c)의 부대역의 크기 성분에 대한 것이다. 그림 3(a)와 (c)는 말랏(Mallot) 트리 방식의 부대역 구조에 대한 것이고 그림 3(b)와 (d)는 쿼드(Quad) 트리 방식의 부대역 구조에 대한 것이다.
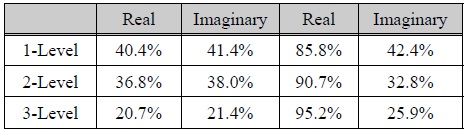
표 1에서는 프레넬릿의 레벨에 따른 LL영역의 집중도를 나타내었다. 프레넬릿 이후 실수, 허수, 형태의 복소항을 웨이블릿 변환을 할 경우 레벨이 높아짐에 따라 LL영역에 집중도가 줄어드는 것을 확인 할 수 있다. 반면에 크기, 위상 형태의 변환할 경우에 크기는 레벨이 높아짐에 따라 LL영역의 집중도가 높아지는 것을 확인 할 수 있으며, 이는 일반 2D 영상에서 나타나는 특징으로 크기항의 경우 2D 기반 영상처리 기법을 적용할 수 있다.
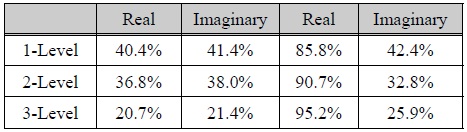
레벨에 따른 LL영역의 에너지 집중도
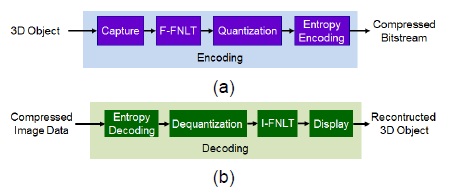
본 장에서는 컴퓨터 생성 홀로그램 기법을 이용하여 획득한 디지털 홀로그램을 FLT을 이용하여 주파수 변환, 자체 제작한 양자화기, 무손실 부호화 기술인 허프만 코딩을 이용하여 데이터를 압축하는 방법에 대하여 소개한다. 그림 4는 제안하는 압축과정을 보여준다. 그림 4(a)는 부호화하는 과정이며, 그림 4(b)는 복호화 하는 과정이다.
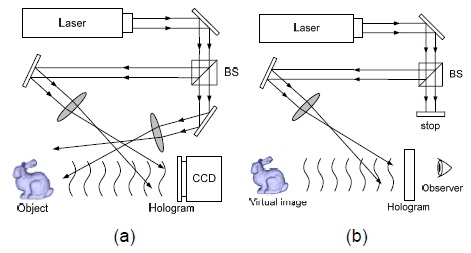
디지털 홀로그램은 과학 장비 대신 전자 장비를 이용하는 방식으로, 홀로그래피의 간섭무늬(interference pattern)를 CCD 카메라에 기록하고 비디오 신호로 전송하여 수신단에서 SLM(spatial light modulator)에 표시된 간섭무늬 데이터에 레이저광을 조사함으로써 영상을 재상하는 기법이다. 그림 5에서 디지털 홀로그램의 시스템 구성을 보이고 있다. 그림 5(a)는 홀로그램을 획득하는 과정이고, 그림 5(b)는 객체 영상을 복원하는 과정이다. 디지털 홀로그램은 기존의 광학 홀로그램에 의한 기법과 동일하게 레이저광을 집광 렌즈로 평행광을 만들고, 빔 분리기(beam splitter, BS)로 참조파(reference wave)와 객체파(object wave)로 나눈다. 객체파는 객체에 조명 된 다음 참조파와 직접 CCD에 조사되어 간섭무늬 즉 프린지 패턴을 형성한다.
간섭무늬 정보는 SLM에 인가되고 여기에 평행광을 조사하면 1차 회절광이 발생하여 3차원 객체를 재상할 수 있다.
3.2.1. 부대역 선택
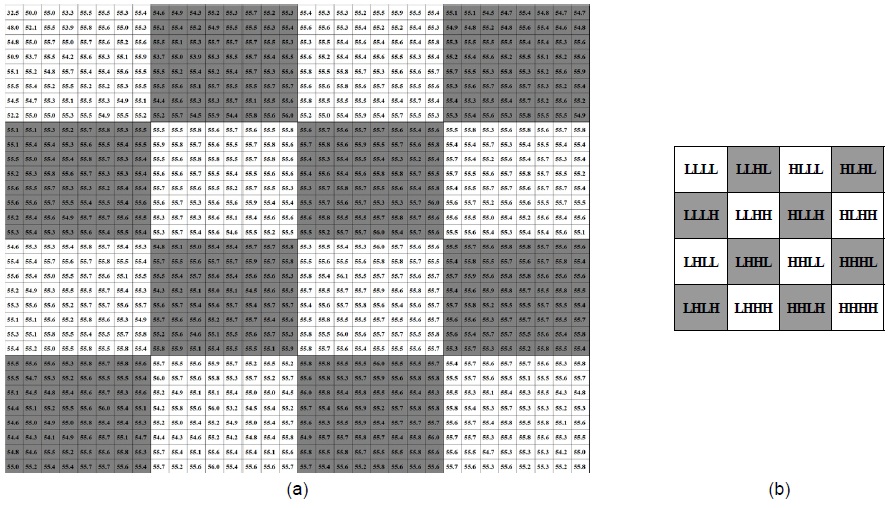
획득한 디지털 홀로그램을 프레넬릿 변환 후 각 부대역에 대하여 양자화를 적용하기 위해서 그림 6의 실험 결과를 통하여 각 부대역의 중요도에 대한 우선순위를결정하였다. 그림 6은 각 부대역의 중요도에 대한 우선 순위를결정하기 위해서 하나의 부대역에 대하여 0-비트로 양자화를 적용하고 나머지 부대역은 양자화를 하지 않고 원본 복원 객체와 비교하면서 PSNR(Peak-Signal-to-noise ratio) 값을 측정한 결과이다. 예를 들어(0,0)에 32.5dB의 값이 적혀 있는 것을 확인 할 수 있다. 이것은 그 부대역에 대해서만 0-비트로 양자화를 하고 나머지 부대역에 대해서는 프레넬릿 계수 그대로 복원을 하여 원본 복원 객체와 PSNR을 측정한 값이다. 0-비트를 할당하는 것은 해당 부대역에 대한 정보를 부여하지 않는다는 것으로 해당 부대역의 정보는 모두 영값으로 처리하였다.
본 논문에서는 저-압축률에서부터 고-압축률을 구현하고자 그림 6에 대하여 임계값 별로 부대역을 선택하는 개수를 다르게 하였으며, 그 단계는 17단계로 구현하였다. 임계값의 범위는 54.0dB 미만에 해당하는 부대역 선택에서부터 56.0 이상에 해당하는 모든 부대역을 선택하는 범위까지이다.
3.2.2. 다이나믹 영역의 설정
부대역의 특성을 파악한 후에 양자화를 설계하기 위한 다이나믹 영역(dynamic range, DR)을 설정하여야 한다. 식 (4)는 다이나믹 영역을 설정해주기 위한 표준편차(σ) 값을 나타낸다. 식 (4)에서
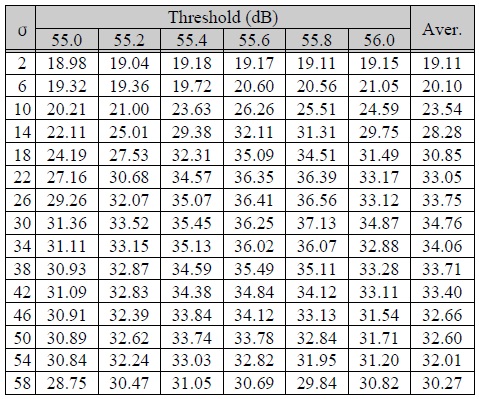
표 2은 그에 대한 PSNR 결과 값을 보여준다. 표 2에 대한 실험은 일정 임계값 미만에 해당하는 양자화기에서 σ=2 부터 σ=58 까지 증가시키면서 PSNR 값을 측정하였다. 그 결과 평균값(Aver.)을 확인해보면 σ=30에서 34.76dB로 가장 높은 PSNR 값을 가지는 것을 확인할 수 있다.
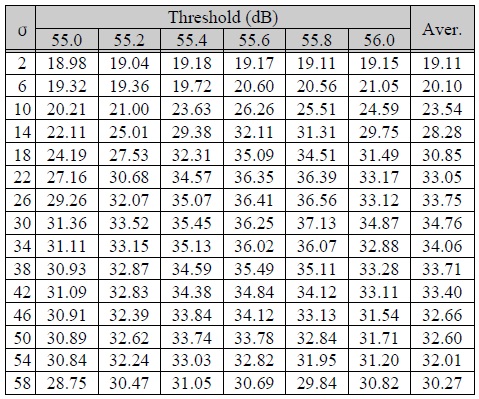
표준편차(σ)에 따른 PSNR
3.2.3. 양자화기의 설계
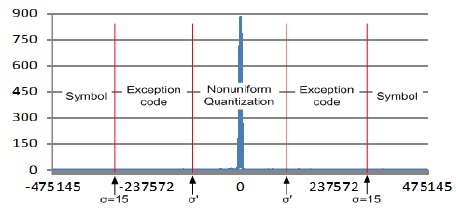
설계하고자 하는 양자화기는 비균일 스칼라 양자화기로 프레넬릿 계수들은 각 부대역에 할당된 비트수에 맞게 양자화 인덱스(index)로 치환되는 방식이다. 정해진 양자화 영역을 벗어나는 프레넬릿 계수들은 빈도수는 작으나 큰 값이므로 PSNR에 많은 손실을 가져올 수 있다. 따라서 중요도를 고려하여 예외 영역이라 설정하고 이에 속하는 계수들을 예외 인덱스(exception index)라 하여 양자화를 거치지 않고 직접 계수를 전송한다. 그 결과로 압축율은 다소 감소하지만 PSNR이 약 2dB 정도 상승하는 효과를 얻었다. 양자화기는 각 부대역의 히스토그램 분석을 통해 표준편차를 계산하고 그림 6과 같은 PSNR의 상관관계로부터 부대역에 비트를 할당하였다.
표 2에서 다이나믹 영역이 σ=30일 때, 가장 좋은 PSNR 값을 갖는 것을 확인하였다. 그래서 ‘’값을 기준으로 σ=15로 표시하였으며, 또한 σ′는 예외 영역의 범위를 설정하는 값으로 예외 영역의 범위에 따라 PSNR 대비 압축율이 많이 달라지기 때문에 4장에서 σ′에 대한 값을 결정하기 위한 실험을 하였다.
본 논문에서 사용한 디지털 홀로그램에 대한 데이터는 표 3에 나타내었으며, 디지털 홀로그램은 CGH 수식으로 생성하였다. 디지털 홀로그램은 200×200[

실험환경
그림 8은 실험에 사용된 디지털 홀로그램의 예제 영상을 보이고 있다. 그림 8(a)은 Rabbit 영상의 디지털 홀로그램이고, 그림 8(b)은 그림 8(a)에 FLT을 적용한 결과이다. 그림 8(c) 양자화 된 결과이며, 그림 8(d)은 그림 8(c)에 양자화기가 적용된 결과 영상이다. 그림 8(b)는 왼쪽의 DC 영역을 확대하여 나타낸 것이다.
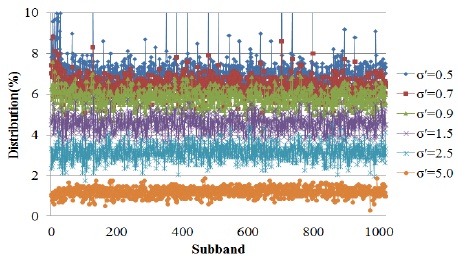
본 논문에서는 양자화를 할 때, 적은 빈도수를 가지나 큰 값을 갖은 계수들은 예외 인덱스를 이용하여 처리하였다. 그림 7에 표시 된 예외영역 범위를 다음과 같이 σ′을 이용하여 조절하였다. 그림 9는 예외 인덱스에 대한 분포를 나타내준다.
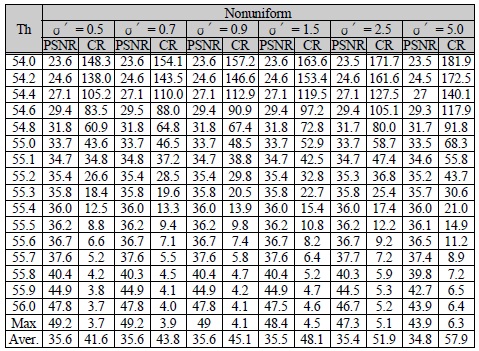
σ′=0.5일 때는 전체 계수분포에 평균적으로 7.1% 의 예외 인덱스를 포함하였고, 점차 감소하여 σ′=5.0 일 때는 1.2%를 포함하였다. 표 4은 σ′의 값을 0.5부터 5.0까지 증가시키면서 PSNR 대비 압축율(Compression ratio, CR)을 계산한 값들을 보여준다. Max은 최상의 LL영역을 제외한 모든 부대역을 선택하여 양자화 한 양자화기를 말한다. 표 4의 결과를 보면 σ′이 값이 증가할수록 16-비트로 표현한 예외영역이 줄어들기 때문에 그 만큼 압축율이 증가하는 것을 확인 할 수 있다. 하지만 그에 비해 PSNR은 낮아지기는 하지만 그 값이 미세한 것을 볼 수 있다.
[표 4.] 예외영역 범위에 따른 PSNR 대비 압축율
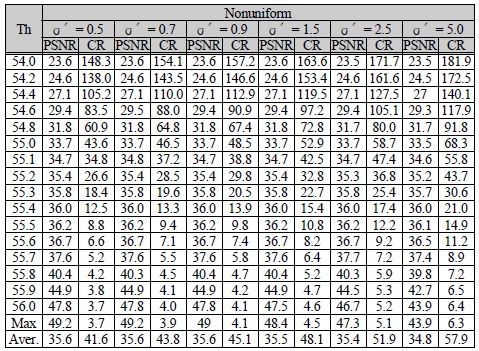
예외영역 범위에 따른 PSNR 대비 압축율
설계한 양자화를 이용하여 계수에 양자화를 수행한 이후에 압축율을 측정하기 위해서 양자화 계수의 발생 확률에 따른 호프만 코드 테이블을 만들었다. 각 양자화 계수별로 허프만 코드를 할당하는 방식으로 엔트로피 코딩을 수행하였다[16].
그림 10은 부대역에 대해 비트를 할당한 예시를 보여 준다. 그림 6에 나타낸 PSNR을 기준으로 하여 부대역에 대한 평균 PSNR이 일정 임계값(Threshold, Th) 미만이면 2-비트로 할당하였고, 그렇지 않은 경우에 0-비트를 할당하였다.
그림 6에서와 같이 최상위 LL영역을 양자화하게 되면 PSNR 값이 많이 떨어지기 때문에 최상위 LL영역은 부대역의 특성을 고려하여 양자화를 하지 않고, 프레넬릿 계수 그대로 보존하였다.
그림 11은 예외영역 범위 중 가장 압축율이 좋은 σ′가 5.0일 때를 선택하여 양자화하고 복원한 객체영상이다. 그림 11(d)부터는 PSNR 값이 30dB이상이 되는 것을 확인 할 수 있지만, 그림 11(a)의 원본객체 영상과 비교해 보면 많이 열화 된 것을 확인 할 수 있다. 원본영상과 비교해 볼 때, 열화 된 정도를 많이 느낄 없는 영상은 그림11(f), (g), (h), (i)이다.
그림 12에는 여러 홀로그램에 대해 제안한 양자화기를 적용한 결과를 나타내었다. 그림 12에서 사용된 홀로그램도 그림 11의 홀로그램과 마찬가지로 CGH를 이용하여 생성한 것에 해당한다. 그림 12(a), (c) 및 (e)는 원본 홀로그램을 복원한 객체 영상을 나타내고, 그림 12(b), (d) 및 (f)는 54.2dB 미만에서의 σ′을 적용했을 경우에 대한 결과를 나타낸다.
본 연구에서는 프레넬릿 변환을 이용하여 디지털 홀로그램을 압축하는 경우에 적용할 수 있는 새로운 형태의 양자화기를 제안하였다. 프레넬릿 변환 이후 각각의 부대역의 에너지 분포 특성을 파악하여 다이나믹 레인지를 설정하였다. 다음으로 PSNR을 향상하기 위해 예외 인덱스를 도입한 후에 최적의 압축율과 PSNR을 구하기 위해서 예외영역 부분의 범위를 조절해가면서 실험을 진행하였다. 그 결과 σ′ = 5.0인 범위에서 높은 성능을 가질 수 있는 양자화기를 설계하였다.
본 논문에서는 σ′ = 5.0에서 최소 6.3:1부터 최대 181.9:1까지 압축을 수행하였고, 이를 복원한 후에 PSNR을 이용하여 수치적인 결과를 분석하였다. 각 결과들에 대해서 시각적인 분석도 수행하였다. 홀로그램의 전용변환 기법으로 이제 막 연구되기 시작하고 있는 프레넬릿을 위한 양자화기는 앞으로 디지털 홀로그램의 부호화를 위한 연구에 다양한 방법으로 적용이 가능하고, 응용이 가능할 것으로 사료된다.