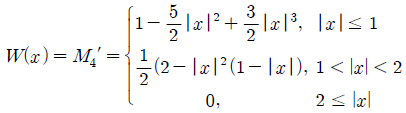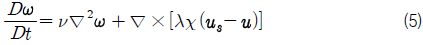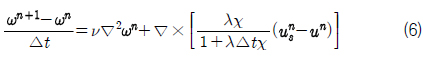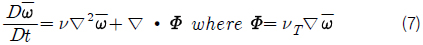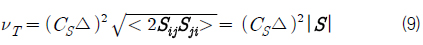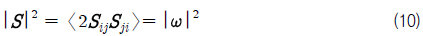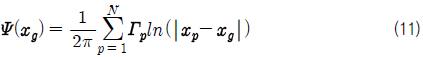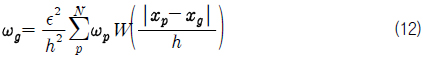Vortex shedding which is the dominant feature of body wakes and of direct relevance to practical engineering problems, has been intensively studied for flows past a circular cylinder. In contrast, vortex shedding from a hydrofoil trailing edge has been studied to much less extent despite numerous practical applications. The physics of the problem is still poorly understood. The present study deals with Kármán vortex shedding from a truncated trailing-edge hydrofoil in relatively high Reynolds number flows. The objectives of this paper are twofold. First, we aim to simulate unsteady turbulent flows past a two dimensional hydrofoil through a hybrid particle-mesh method and penalization method. The vortex-in-cell (VIC) method offers a highly efficient particle-mesh algorithm that combines Lagrangian and Eulerian schemes, and the penalization method enables to enforce body boundary conditions by adding a penalty term to the momentum equation. The second purpose is to investigate shedding frequencies of vortices behind a NACA 0009 hydrofoil operating at a zero angle of attack.
프로펠러 날개 뒷날에서 발생하는 명음(singing) 현상에 대한 연구는 선박유체 분야에서 오랜 시간 동안 다루어지고 있는 연구 주제 중의 하나이다. 프로펠러 명음 현상은 날개 뒷날에서 박리되는 와도 흘림(vortex shedding)과 밀접한 관계가 있다. 명음 현상은 와도 박리의 발생 주파수와 날개 고유 주파수가 서로 일치하는 경우에 공진 현상에 의해 발생한다. 일반적으로 진동계는 외부 가진에 의해 진동이 발생하지만, 외부 가진 없이 진동이 유발되기도 하며 이러한 진동을 자려 진동(self-excited vibration)이라 한다. 대표적인 예는 전선이나 해저 송유관 등에서 발생하는 갤러핑(galloping) 현상이며 명음 현상 역시 자려 진동에 해당된다. 와도 흘림 현상에 의한 자려 진동은 일정한 유입속도 영역에서 특정 주파수 특성을 가지는 구속(lock-in) 현상이 발생함이 보고되고 있다 (Ausoni, 2009; Ahn, et al., 2009).
명음을 방지하기 위해서는 날개의 고유 진동수가 와류 발생 주파수와 불일치되도록 하여야 한다. 최근 수중익 선박이나 프로펠러 추진 선박의 경우 특정 운용속도 영역에서 이러한 명음이 발생하는 사례가 보고되고 있다. 명음 발생은 날개의 국부 공진 현상으로 기계적으로 동일하게 가공된 프로펠러 날개일지라도 특정 날개에서만 발생하기도 한다. 명음의 발생 조건은 아직 명확히 밝혀지지 않아 설계단계에서 이를 방지할 수 있는 대책이 반영되지 못하고 있다 (Ahn, et al., 2009). 명음이 발생하였을 때는 경험적으로 연삭하거나 재가공하여 박리 와류의 특성을 바꾸어 문제를 해결하고 있다 (Kim & Chung, 1994).
본 논문에서는 명음 현상의 발생 메커니즘을 이해하기 위한 연구의 일환으로 2차원 날개 뒷날 근처에서의 와류 유동을 수치적으로 모사하고 이를 통해 와도 흘림 주파수에 대한 특성을 파악하고자 한다. 유동 모사에 사용된 수치해석 방법은 라그랑지안 보텍스 방법(Lagrangian vortex method)을 기반으로 한 하이브리드 입자-격자법(hybrid particle-mesh method)를 사용한다. 보텍스 방법은 와도를 기본변수로 사용하기 때문에 강한 와류 유동 해석에 있어서 유리한 점이 있으며, 무한 원방 조건이 자동으로 만족되기 때문에 와도가 나타나는 곳에 대하여 한정된 계산영역을 택할 수 있는 장점이 있다. 또한 와도-속도 정식화는 비관성 및 관성 좌표계에서의 지배 방정식 형태가 같기 때문에 움직이는 물체에 대한 해석이 용이하다. 보텍스 방법은 유동의 물리현상에 기초한 비교적 간단한 알고리즘으로 구성되지만 일부 적분항에 대한 계산시간이 상당히 소요된다는 점으로 인해 높은 레이놀즈 수 유동 해석에 어려움 있다. VIC(Vortex-In-Cell) 방법과 penalization 방법이 조합된 하이브리드 입자-격자법은 와도의 세기 변화와 속도가 모두 정규 격자계에서 계산되기 때문에 보텍스 방법의 계산 시간을 크게 단축할 수 있다. 특히 penalization 방법은 물체 표면에서의 속도고착조건(no-slip condition)이 만족되도록 물체표면에서의 와도값을 결정하는데 매우 효과적이다. 추가적으로 본 연구에서는 계산시간을 단축하고 가용 컴퓨터 메모리의 효율적인 사용을 위해 병렬계산(parallel computing), 영역분할 방법(domain decomposition), 입자분할 방법(particle-decomposition), 다중영역 방법(multi-domain)과 큐빅 스플라인 보간법(cubic spline interpolation)을 활용한 경계값 추정 방법이 적용되었다. 2장에서 지배방정식과 하이브리드 입자-격자 방법에서 사용되는 수치기법을 소개한다. 3장에서는 순간 출발하는 2차원 수중익 주위의 유동 해석 결과를 보여주며, 수중익 후류에서 나타나는 와도흘림 주파수 특성을 설명한다. 마지막으로 4장에서는 본 연구로부터 얻어진 결과를 정리하고 향후 연구계획에 대해 서술한다.
2차원 비압축성 점성 유동장에서 보텍스방법은 이산화된 와도장을 표현하는 보텍스 입자를 기본 요소로 한다. 와도장은 N개의 보텍스 입자(순환세기
보텍스 입자의 성장과 이동은 식 (2)와 식 (3)에서와 같이 Lagrangian 개념으로 표현된다.
점성유동장의 속도(
여기서 아래첨자
유량함수와 와도간의 Poisson 방정식은 공개 library인 FFTW (Fastest Fourier Transform in the West)를 사용하여 계산된다. 입자 위치에서의 속도는 정규격자상에서 구해진 속도 성분과 보간함수를 이용하여 구한다.
표면 고착조건을 만족시키기 위한 penalty 항이 추가된 Navier-Stokes 방정식은 식(5)와 같다.
여기서
확산항은 보텍스입자의 성장을 표현하며, Penalty 항은 물체 표면에서의 고착조건을 만족하도록 물체 근처의 입자세기를 변경한다. 보텍스 입자의 속도 계산과 같이, 입자세기는 모두 정규 격자계에서 계산되며 변경된 입자세기는 입자위치로 다시 보간된다. 보텍스 입자들은 최종적으로 얻은 속도와 세기를 갖고 이동하게 되며, 이때 시간전진은 midpoint predictor-corrector 방법을 사용하였다.
2차원 유동에 대하여 식 (7)와 같이 표현된 여과된 와도이송 방정식(filtered vorticity transport equation)은 결국 식 (8)과 같이 정리된다 (Mansfield, et al., 1996).
여기서 난류 점성계수
비압축성 유체 (∇·
결과적으로 난류 모델은 유동장 내 각 보텍스 입자의 위치마다 난류 점성 계수
2.1장에서 언급된 것과 같이, 보텍스 입자의 이동 속도는 유량함수와 와도 간의 Poisson 방정식을 통해서 구해지며, 경계에서의 유량함수는 식 (11)과 같이 Green 함수의 해를 이용하여 얻어진다.
여기서
큐빅 스플라인은 n개의 절점과 그 함수값을 바탕으로 절점 간은 3차 다항식으로 표현되고 옆 구간의 다항식에서는 절점에서 1차와 2차 미분값이 연속되도록 표현된다. 끝단조건(end condition)은 2차 미분값이 0인 natural 조건을 사용하였다. 경계에서의 유량함수가 매우 부드럽게 변화되기 때문에 보간법의 적용이 가능하다. 전체 경계점 중에서 일부를 선택하여 경계에서의 유량함수를 식 (11)에 의해 직접 계산하고, 나머지 위치에서의 유량함수 값은 큐빅 스플라인 곡선에 의해 추정된다.
본 연구에서는 각 경계에서 격자점 수의 25%만으로 곡선식을 얻었다. 하지만 경계에서의 격자점 수가 256개보다 작을 경우에는 오차를 줄이기 위해서 식 (11)에 의해 모든 격자점의 유량함수를 직접 계산하였다. 큐빅 스플라인 보간법의 적용으로 FFT 영역 경계에서의 유량함수를 계산하는데 소요되는 시간을 80% 이상 단축할 수 있었다. 예를 들어, 200만개 보텍스입자가 유기하는 4096 격자점의 유량함수를 직접 계산할 경우 40초가 소요되었으나, 1024 격자점의 유량함수를 직접 계산하고 경계에서의 나머지 격자점의 유량함수를 큐빅 스플라인 보간법에 추정할 경우에는 8초 정도 소요된다. 각각의 격자점에서 직접 계산된 유량 함수 값을 기준으로 보간법에 의해 계산된 값은 약 0.01%미만의 오차를 갖는다.
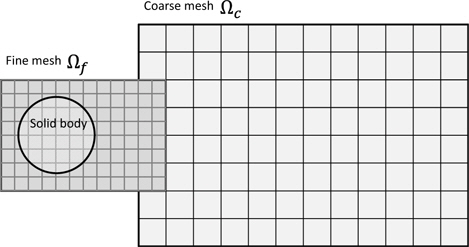
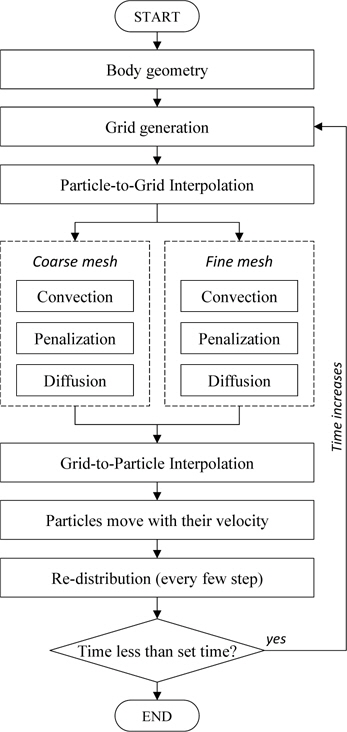
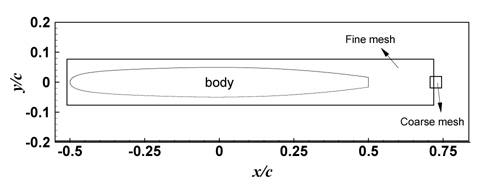
보텍스 방법은 기본적으로 와도가 나타나는 곳에 대하여 한정된 계산영역을 택할 수 있으나 유동이 발달하면서 보텍스 입자는 물체의 후류로 이동되기 때문에 계산영역은 시간이 지나감에 따라 늘어나게 된다. 다시 말해서, 유동이 발달됨에 따라 계산영역은 증가하게 되며, 그에 따라 계산시간이 크게 증가하게 된다. 계산영역의 과도한 증가를 막기 위해서 다중 영역 방법은 유동영역을 다수의 영역으로 분할하여 각각의 영역에서 보텍스 입자의 세기와 속도를 추정하는 방법이다. 본 연구에서 유동영역은 Fig. 1과 같이 물체 주위와 후류 영역으로 나누었으며 분할된 두 개의 계산영역에서의 격자간격은 서로 다르게 사용하였다.
다중 영역 방법에 의해 보텍스 입자의 세기와 속도를 구하기 위해서 보텍스 입자의 세기는 분할된 유동영역을 담당하는 두 개의 정규격자로 보간되어야 한다. 격자 간격이 서로 다른 정규 격자계를 사용하기 때문에 식 (4)는 식 (12)와 같이 다시 표현된다.
여기서
각각의 격자계에서 계산된 보텍스의 속도와 세기는 다시 보텍스 입자 위치에서의 값으로 보간되며, 이때 보텍스 입자의 위치에 따라 보간에 필요한 격자계를 선택한다.
유동해석은 다수의 Intel Xeon64 3.3 GHz 프로세서(CPU)를 사용하여 병렬처리연산을 통하여 수행된다. 병렬계산을 위해서 전체 격자영역은 프로세서의 수에 맞게 분할하여 각 프로세서에 할당한다. 이를 영역분할(domain decomposition)이라 하며, 모든 프로세서는 동일한 성능을 갖는다는 전제하에 전체 계산 영역은 같은 크기로 분할한다. 각각의 프로세서 사이의 데이터 교환에 필요한 시간을 최소화하기 위하여 분할 영역간의 중첩 영역 (overlapping region)의 크기는 2
본 연구에서는 유동 영역을 두 개로 나누어 유동해석이 수행되기 때문에 병렬처리연산을 위한 영역 및 입자 분할은 두 개의 유동 영역(fine mesh와 coarse mesh)에 대해 순차적으로 적용되어 계산된다. Fig. 2는 본 연구에서 사용된 유동 수치해석 방법의 전체 알고리즘을 도시한 것 이다. 레이놀즈 수, 와도 입자와 격자 크기, 물체 또는 유입류의 속도와 같은 계산조건과 해석을 하고자 하는 대상체에 대한 모델링만으로 계산이 시작된다. 다시 말해서, Penalty 항에 의해 물체 주위의 와도값이 결정되기 때문에 판 요소법(panel method)와 같이 물체경계에서의 초기 조건을 구하기 위한 추가적인 유동 해석은 요구되지 않는다. 보텍스 입자들이 서로 너무 멀어지거나 뭉쳐지지 않도록 몇 번의 시간간격마다 보텍스 입자들을 재분배(re-distribution)하여야 한다. 보텍스 입자의 재분배는 식 (4)를 사용하여 보텍스 입자 크기와 동일한 격자 간격을 갖는 격자계에 보간된다. 이때의 격자계는 보텍스 입자를 모두 포함하여야 한다. 균일한 간격으로 재분배된 보텍스 입자는 그 세기에 따라 선택되며, 본 연구에서는 최대 보텍스 입자세기의 0.01% 이상의 세기를 갖는 보텍스 입자를 선택하였다. 순환세기 보존을 위해 제거된 입자들의 세기의 합은 선택된 입자들로 입자 세기에 비례하여 나누어준다. 2.1장에서와 같이 보간 함수(interpolation kernel function)로 0차, 1차, 2차 모멘트가 보존되는
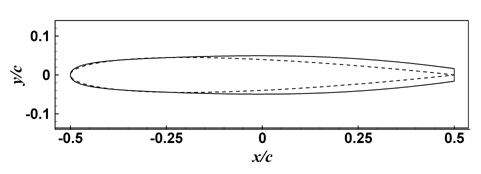
본 연구에서는 하이브리드 입자-격자 방법을 이용하여 순간적으로 출발하는 2차원 수중익 주위의 점성 유동을 해석한다. 해석에 사용된 2차원 단면 형상은 Fig. 3에서와 같이 날개 단면의 뒷날이 절단된 NACA 0009이며, Ausoni (2009) and Zobeiri, et al. (2012) 실험에 사용한 단면과 동일하다. 코드 길이(c)는 날개 단면의 앞날부터 뒷날의 절단면 위치까지를 의미하며, 절단면의 두께(
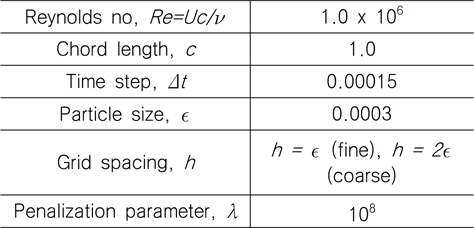
초기 보텍스 입자 분포 및 격자는 Fig. 4와 같이 분포 된다. 물체 주위 유동 해석을 담당하는 미세(fine) 격자의 위치는 (−0.5103, 0.7185) x (−0.0768, 0.0768)이며, 격자수는 4096 x 512 이다. 미세 격자의 x-방향 크기는 고정되며 y-방향 크기는 보텍스 입자 분포에 따라 증가되거나 감소된다. 후류에 놓인 성긴(Coarse) 격자는 유동의 발달에 따라 크기가 결정되며, 보텍스 입자가 미세 격자 내에만 위치할 경우에는 성긴 격자에서의 계산은 무시된다. 수치해석 조건은 Table1과 같다.
[Table 1] Numerical parameters
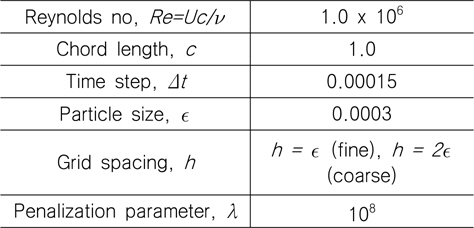
Numerical parameters
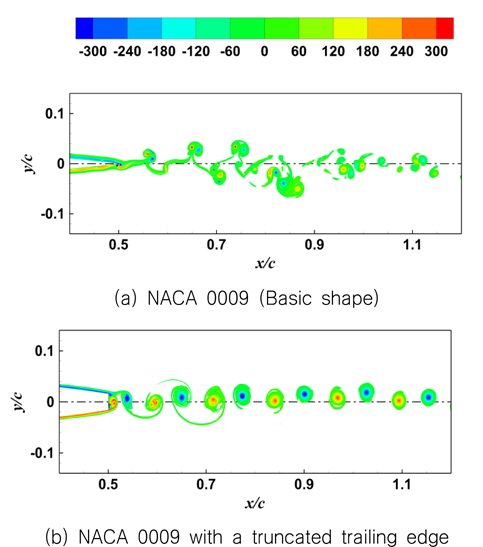
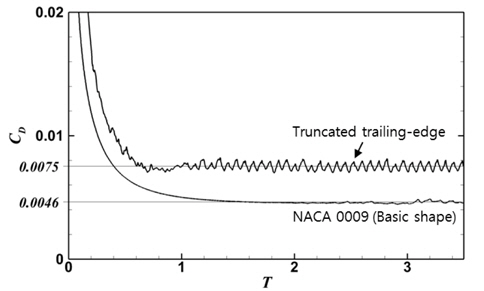
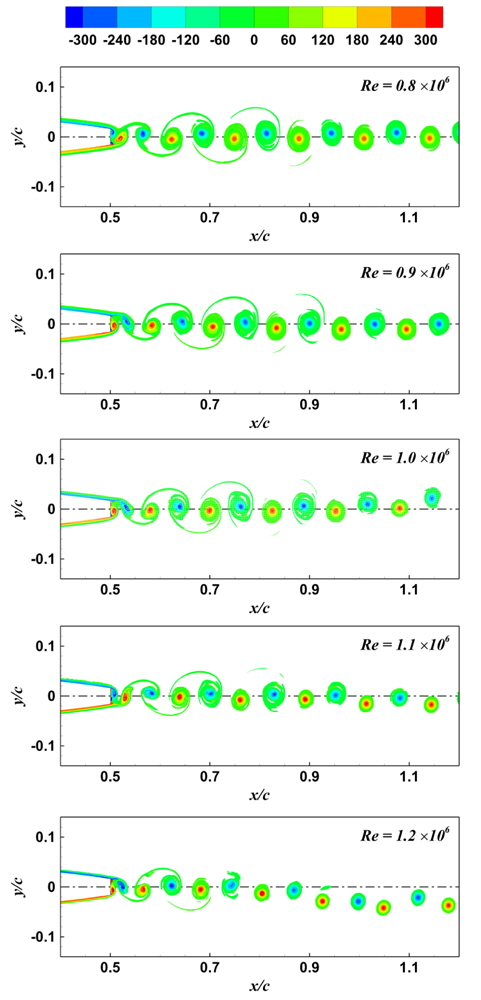
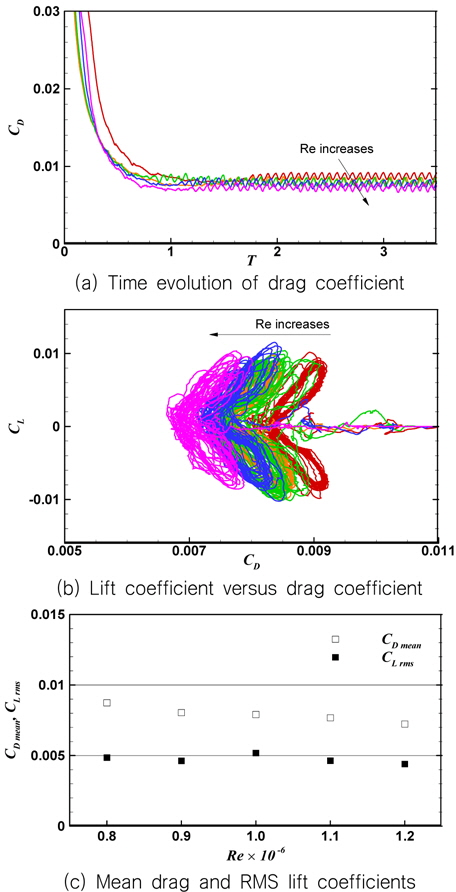
유동해석은 16개의 Intel Xeon64 3.3 GHz 프로세서를 사용하여 무차원 시간 T=3.5 까지 수행하였다. Fig. 5는 기본형상의 NACA 0009 과 뒷날이 잘린 형상에 대한 와도 세기 및 분포를 보여준다. 뒷날이 잘린 NACA 0009에서의 와도값이 상대적으로 크며, 뒷날에서부터 매우 규칙적으로 와도가 생성되는 것을 볼 수 있다. Fig. 6은 유동 발달에 따른 항력 변화를 나타내었다. 두 경우의 유동장 모두 무차원 시간 1.5이후부터 안정되었으며, 뒷날이 잘린 날개의 항력이 규칙성을 갖는 것을 볼 수 있다. 기본 형상의 항력은 0.0046으로 추정되었으며, XFOIL(version 6.99)의 항력값 0.0043와 비교하였을 때 큰 차이를 보이지 않았다. 뒷날이 잘린 2차원 날개의 평균 항력은 0.0075이며, 기본형상과 비교하였을 때 뒷날의 형상에 의해 항력이 증가되고 있다.
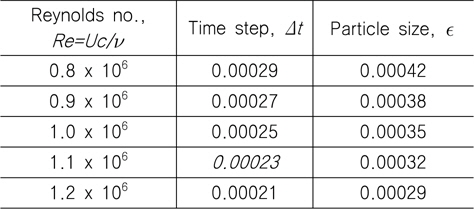
레이놀즈 수의 영향을 알아보기 위해 레이놀즈 수 0.8~1.2 x 106에서 유동해석을 수행하였으며, 시간전진 및 유체입자 크기는 Table 2에 정리하였다. 해석조건의 일관성을 위해 근사적으로 y+가 15가 되도록 입자 크기를 결정하였으며 시간간격(Δt)는
[Table 2] Time step and fluid particle size at five different Reynolds numbers
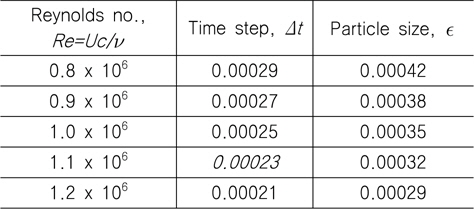
Time step and fluid particle size at five different Reynolds numbers
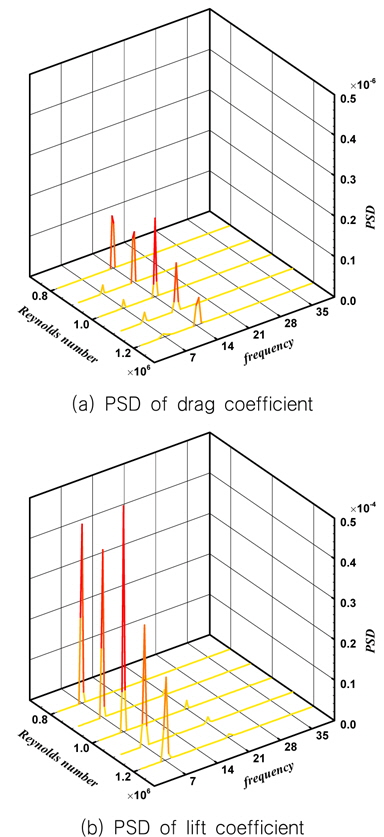
Fig. 10은 레이놀즈 수 변화에 따른 Strouhal 수를 나타낸다. Strouhal 수(
Fig. 10에서 수치해석으로 추정된 Strouhal 수는 Ausoni (2009)의 실험에서 계측된 Strouhal 수보다 작다. 레이놀즈 수 1.0x106 에서 추정된 Strouhal 수는 실험값과 비교하여 약 10%의 오차가 있다. 이는 2차원과 3차원의 차이에서 비롯된다고 추측된다. Smagorinsky 상수와 penalization 상수와 같은 계산에 필요한 주요 상수는 와도흘림 주파수에 대한 영향이 거의 없었다. 서로 다른 상수를 사용할 경우에는 유동 발달 초기에 발생하는 유동현상의 차이에 의해 와도흘림의 주기성이 나타나는 시점이 다소 다르게 나타나지만, 주기성이 나타난 이후에는 와도의 강도뿐만 아니라 흘림 주파수에 대한 영향이 없었다. 격자 및 시간 간격이 다른 계산 조건에서도 와도 흘림 주파수에는 차이가 없었다. 또한, Ausoni (2009)와 Zobeiri, et al. (2012)의 시험에서 사용된 날개 모형의 스팬(span, s)과 코드길이(chord length, c)는 각각 150mm와 100mm로, 코드길이에 대한 폭의 비(aspect ratio)는 s/c=1.5이다. 상대적으로 aspect ratio가 크지 않았다. 일반적으로 aspect ratio는 유동의 와도생성에 영향을 미치며 레이놀즈 수에 따라 그 영향의 정도는 다르다 (Szepessy & Bearman, 1992). 작은 aspect ratio는 벽면에 의한 3차원 효과가 상대적으로 강하게 나타날 수 있다.
Ausoni (2009)의 결과는 3차원 날개의 후류에서 유동을 LDV로 계측한 결과로부터 와도흘림 주파수를 산출하였으며, 본 계산은 날개 주위의 유동을 2차원 유동으로 가정하고 계산된 결과이다. 뒷날이 잘린 날개 후류는 난류 유동이며 난류는 분명히 3차원 유동현상이다. 2차원으로 가정된 난류 유동은 폭 방향(spanwise)으로 난류 에너지 교환이 없기 때문에 난류유동을 2차원으로 가정한 것은 모순일 수 있다. 하지만 상대적으로 3차원 유동 특성이 적은 경우에는 2차원으로 유동을 가정하면 계산 비용을 크게 줄일 수 있기 때문에 2차원 난류 유동해석이 일부 연구에서 사용되기도 한다. Fig. 10은 날개 뒷날에서 발생하는 와도흘림 현상이 2차원 난류 해석으로 근사적으로 예측할 수 있음을 보여준다.
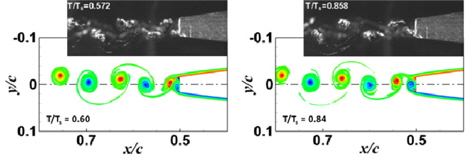
Fig. 11은 레이놀즈 수 1.2x106 유동에 대하여 Zobeiri, et al. (2012)의 유동가시화 결과와 본 연구에서의 계산 결과를 비교한 것이다. 결과 비교를 위해 계산결과의 좌표축은 반대로 나타내었다. Zobeiri, et al. (2012)의 유동가시화 결과는 캐비테이션 발생 조건 (
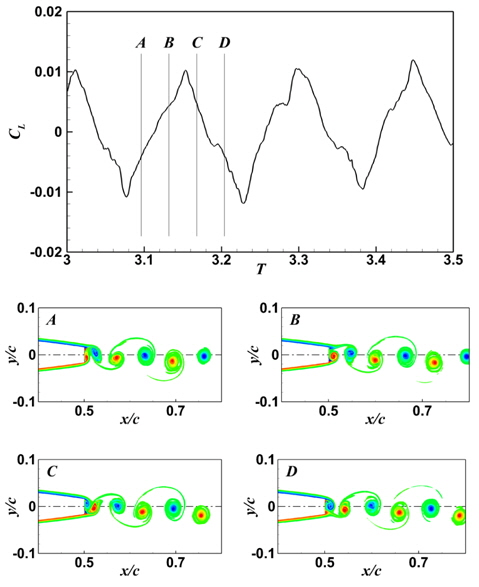
Fig. 12는 레이놀즈 수 1.2x106 유동에 대한 와도장을 보여주며, Fig. 12의 A와 C는 와도장이 서로 대칭 관계이며 이에 따른 양력 계수도 서로 반대 부호의 값을 갖는다. 또한, Fig. 12의 B와 D에서의 결과도 같은 양상을 보인다. 이는 날개 뒷날에서 와도의 발생이 매우 규칙적이고 윗날과 아랫날에서 서로 대칭적으로 와도가 발생하고 있음을 보여준다.
본 연구에서는 2차원 NACA 0009 수중익에 대한 유동 수치해석을 위하여 하이브리드 입자-격자 방법을 적용하였으며, 계산시간 단축과 가용 컴퓨터 자원의 효율적 사용을 위한 수치기법을 적용하였다. 이를 통하여, 상대적으로 높은 레이놀즈 수 유동에 대한 수치모사가 가능했다.
뒷날이 수직으로 잘린 2차원 날개는 뒷날에서 와도 현상을 매우 잘 나타나기 때문에 와도 현상을 모사하기 위한 수치기법을 검증하는 목적으로 선택되었으며, 하이브리드 입자-격자 방법을 통해 얻어진 유동장과 양항력으로부터 와도흘림 주파수를 구하였다. 하이브리드 입자-격자 방법을 통하여 2차원 날개 뒷날에서의 와도흘림 현상을 성공적으로 모사하였으나, 무차원화된 와도 흘림 주파수는 타 연구자의 실험값과 비교하여 10% 내외의 오차가 있었다. 주된 오차의 원인은 본 연구에서의 계산이 2차원으로 수행하였기 때문으로 판단된다. 뒷날이 잘린 날개 후류는 난류유동이며 난류는 분명히 3차원 유동현상이기 때문에 유동을 2차원으로 가정한 본 연구에서의 가정은 모순이 있다. Ausoni (2009)는 실험에서 상대적으로 작은 aspect ratio를 갖는 모형을 사용하였다. 보다 면밀한 연구를 위해 3차원 유동해석이 요구되지만, 본 연구를 통하여 날개 뒷날에서 발생하는 와도흘림 현상이 2차원 난류 해석으로 근사적으로 예측할 수 있음을 보였다. 이는 상대적으로 적은 계산비용으로 날개 뒷날에서 발생하는 와도흘림 주파수를 근사할 수 있다는 점에서 매우 효율적인 접근이 될 수 있다. 향후 하이브리드 입자-격자 방법은 3차원 유동해석을 위해 확장될 것이며, 3차원 난류해석을 통하여 날개 뒷날에서의 와도흘림 현상을 보다 상세하게 연구하고자 한다.