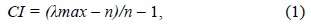The market size of the world’s defense industry is expected to increase from approximately $361 billion in 2012 to approximately $406 billion in 2015. Further, the acquisition and sales of weapon systems are expected to be more competitive in the future partly due to the reduction in the defense budget (either buyer’s or seller’s) and the general global economic crisis [1]. For example, the US has recently decided to cut its defense budget by $47.8 billion; this will influence not only the US defense industry but also other countries that want to purchase weapon systems from the US. Therefore, these countries (including Korea) should promote their defense industry in order to retain competitiveness through a selection of the best business partners.
Hence, the selection and evaluation of the suppliers/ business partners that can provide the necessary technology and quality products that satisfy the requirements of the buyer is one of the key activities in decision making related to the strategic purchasing in the defense industry [2]. However, this selection process is complex, has multiple objectives, and requires an analysis of both quantitative (e.g., price) and qualitative factors (e.g., technology transferability) as well as internal and external policy constraints. The reasons for this complexity include the deregulation of the countries, rapid development cycle, product complexity, rapid technical progress, and the customers’ high demands[3].
Korea is currently undertaking its third purchase of the next-generation fighter (F-X, Fighter-eXperimental) that cost approximately $8.3 billion in 2014. In selecting a supplier/business partner for the project, the Korean government wants to reduce risk and maximize the whole value as a buyer. This selection process requires a series of strategic analyses, which is an important concern to both military personnel and policy makers.
However, an efficient and effective selection process in the defense industry is lacking in Korea partly due to the general practices followed by the Korean government. In Korea, when the government announces the need for military projects regarding research and development, or procurement of military products, the suppliers need to meet the government’s requirements. Because of this practice, there have been many failure cases. In these cases, it was very rare that everything happened as originally planned. Rather almost all projects had been modified in the middle of their execution, which resulted in project delays, increasing costs, and waste production. Therefore, it is necessary to develop and implement a system for selecting suppliers/business partners efficiently and effectively.
The purpose of the study is to suggest a method that can improve the selection process. In particular, in this study, we propose the application of a data envelopment analysis–analytic hierarchy process (DEA-AHP) integrated model in the selection process of the next-generation fighter system (the 3rd FX) in Korea.
The rest of this paper is organized as follows: the next section discusses the general environment of the acquisition of weapon systems in Korea. The following sections present a discussion of an integrated model, an actual application of the proposed model in the selection process of the nextgeneration fighter system in Korea, and the survey results. The last section presents the conclusions and the future implications of this study.
>
A. Acquisition of a Weapon System
Military products are largely classified as weapon and non-weapon systems. The weapon system includes all the field weapons (e.g., guided weapons, aircrafts, and vessels) and all other operating products (e.g., parts, facilities, and software) that are necessary in a war. The non-weapon system includes all the elements other than the ones that are classified as the weapon system (e.g., equipment, parts, facilities, software, and materials).
The acquisition is categorized as either a domestic acquisition that purchases internal products or a foreign acquisition that purchases foreign products. The foreign acquisition in Korea is further categorized as either foreign military sales (FMS) or foreign company purchases (FCP). FMS is an acquisition that is controlled and guaranteed by the US government through a contract between the US and Korea. FCP, on the other hand, is a direct acquisition from foreign companies without any government involvement [3,4].
The two most common contract methods that follow the national contract law in Korea are the lowest bidding and negotiation. The lowest bidding method is a basic method, and the negotiation method is acceptable in a special case according to the national contract law. Even though the lowest bidding method selects the lowest bidder, some big projects that are above a certain level also utilize screening tests to test the capability of the bidder.
Typically, the procedure for selecting suppliers follows several phases: 1) the assessment readiness and the assessment of a proposal, 2) the evaluation of the products, 3) negotiation, and 4) the final selection.
The assessment readiness for a project consists of writing the request for proposal (RFP), the announcement of bidding, the formation of the assessment committee, and the development of an assessment plan including the assessment criteria. One difference between a purchasing project and an R&D project is that the former assesses each item for a specific project (e.g., selecting the next-generation fighter system), and the latter assesses the common items that are equally applicable to all future projects.
There are necessary and optional conditions in a purchasing project. The necessary conditions are essential items for the required operational capability (ROC) and should be satisfied. The optional conditions are the assessment items other than the necessary conditions and should satisfy a certain level of satisfaction (generally, 70%) on the RFP. ROC is used for determining what the Korean government wants to purchase in terms of the capabilities of the weapons. Once the ROC is complete, the Ministry of National Defense makes a budget and initiates the procurement process so that the potential suppliers can enter the bidding process. The RFP is a solicitation made often through a bidding process by an agency or company interested in the procurement of a commodity, service, or valuable asset, to potential suppliers to submit business proposals. It is submitted early in the procurement cycle either at the preliminary study or the procurement stage. The RFP presents preliminary requirements for the commodity or service and may dictate to varying degrees the exact structure and format of the supplier’s response. Effective RFPs typically reflect the strategy and short-/long-term business objectives, providing detailed insight upon which suppliers can offer a matching perspective [5].
After assessing the proposal, the government evaluates the products to select initial products that satisfy all necessary conditions and meet or exceed the suggested level requirements for optional conditions. Therefore, usually, multiple products are selected at this stage. A negotiation process then follows on the basis of factors such as price, technology, and general conditions.
Then, the government selects the final product by typically applying either the lowest cost while satisfying the requirements of the ROC method or the comprehensive evaluation method. The former is the most common method, but the latter can be used when the comparison between the suggested products is complex and/or when the project is so big that it requires many strategic considerations. The RFP usually includes the determination method in the original announcement of bidding. Then, a provisional contract is signed by both parties (i.e., the Government and the suppliers).
In a big investment case such as the acquisition of a weapon system, the failure of the project lays a lot of burden on both the buyer and the seller [6,7]. However, because of the unique characteristics of the military industry, neither party acknowledges its mistakes. Therefore, the reasons for failure are not available to the public and not much has been done to analyze the failures.
However, a failure analysis is necessary because its learning effects are very helpful for future project management. The causes of project failures can include errors of cost analysis, improper setup of the operational concept, unrealistic targets, and miscommunication between the project manager and the supplier to name a few. However, the most common cause of the project failure is found in the phase of selecting suppliers/business partners. The following section discusses decision-making models that can be used in the selection process.
>
C. The Third FX Project in Korea
Recently, the Korean government selected F-35A as the next-generation fighter system. The general selection process is as follows: first, the government investigated many candidates including F-35A, F-15SE, and Euro-Fighter. After evaluating for more than two years, the government selected F-15SE as the next-generation fighter system in August 2013. After this decision, there were considerable opposition from the press and the national security experts, including the former Air Force Chief of Staff, partly because F15-SE lacked stealth capabilities. Then, the Korean government re-negotiated for about five months and finally, selected F-35A as the next-generation fighter system. This is a good example that shows why we need a more systematic decision-making process; in this paper, we try to shed light on such studies. The following section introduces two of the most widely used decision-making models, which will be incorporated in our study.
>
A. Data Envelopment Analysis
DEA measures efficiency by computing the extent to which 1) production can be increased by keeping the inputs constant or 2) the use of inputs can be decreased keeping the production constant. The DEA model has some variations including CCR (Charnes, Cooper and Rhodes) ratio, CCR multiplier, and CCR envelopment models. This study applies the CCR multiplier model to transform a non-linear program model into a linear program model. Then, we utilize the CCR envelopment model to identify a frontier group among many candidates. In other words, the model performs the efficiency measurement on each decision-making unit (DMU) by comparing a unique weighted value of inputs and outputs using a linear programming technique.
However, it is difficult to quantify the input and output factors. The qualitative factors are also dominating factors. Therefore, a decision cannot be made by evaluating only the mechanical and technological factors. Hence, the DEA method is good at finding an initial frontier group among many alternatives.
This model finds the most efficient group without assigning any weighted values in advance by deleting alternatives that cannot be superior even if any combination of weighted values are assigned to them. In other words, the model finds and deletes alternatives that cannot be superior to others under any circumstances, and then, it discriminates between the relative efficiency of the remaining alternatives through ‘proof to the contrary’ technique [8].
>
B. Analytic Hierarchy Process
AHP is a method that improves the inefficiency in the decision-making process [9,10]. It is part of a decision support system that systematically assesses alternatives when there are multiple and complex objectives and/or the evaluation criteria. Such criteria can be either quantitative or qualitative, and AHP can measure these criteria as proportional scales after quantifying these qualitative criteria. Therefore, the method can be used in non-standard and complex problems. In fact, Saaty [10] argues that the AHP is a useful decision-making tool in a complex decision-making situation with multiple objectives, evaluation criteria, and participating decision makers. The process determines the priority of the alternatives through a series of pair-wise comparisons after categorizing the criteria into multi-hierarchical levels.
Vargas [11] asserts that the theoretical underpinnings of AHP lie with four axioms: reciprocal comparison, homogeneity, independence, and expectations. The reciprocal comparison axiom means that decision makers should be able to make pair-wise comparisons of two factors in the same hierarchy in terms of preferences and the reciprocal strength of the preferences should exist. Homogeneity means that the preferences should be expressed by means of a bounded scale. Independence means that the criteria should not be related to the properties of the alternatives. Expectations mean that the hierarchical structure is assumed to be complete.
Because of its usefulness and simplicity, AHP has been used in various decision-making situations including marketing [12], project and risk management [13], strategic planning [14], information technology selection [15], employee recruitment [16], production [17], and medical and healthcare [18].
Typically, AHP has five phases: 1) formation of hierarchy, 2) pair-wise comparison of the factors and alternatives, 3) estimation of the weighted values, 4) consistency check, and 5) selection of the best alternative. In the first phase, a decision hierarchy is formed. The goal is at the top level followed by the evaluation criteria and the alternatives are at the bottom [9,10]. The evaluation criteria sometimes have sub-criteria.
In the second phase, a series of pair-wise comparisons between the factors in the same hierarchy are implemented to determine the priority of the factors from the viewpoint of the upper-level hierarchy. Further, in this phase, the pairwise comparisons between alternatives are performed to obtain the initial priorities of the alternatives.
In the third phase, the weighted value for each factor is determined using the eigenvalue method. The weighted values are subjective, and this relative judgment cannot guarantee the internal consistency. Therefore, the consistency of the judgment is evaluated in the following phase.
The consistency of the decision makers (i.e., whether the judgments made by each decision maker are logically consistent or not) is evaluated in this phase. If, for example, a certain decision maker’s judgment is such that alternative A is more important than alternative B, and alternative B is more important than alternative C, then it is considered consistent. This can be found out by calculating the consistency index (CI) and the consistency ratio (CR) for the evaluation criteria. CI and CR can be calculated by the following formula and considered to have rational consistency if CR is less than 0.1, acceptable consistency if it is less than 0.2, and deficient consistency otherwise.
where λmax denotes the maximum eigenvalue of a pair-wise comparison matrix.
where the random index (RI) is a CI calculated by a computer simulation based on non-consistent pair-wise comparisons.
In the final phase, a comprehensive vector of importance is calculated to determine the priorities of the alternatives. First, the vector of importance between factors in each layer is multiplied by the vector of importance on each factor’s alternative. Then, the rankings of each alternative are determined and the alternative with the highest ranking is selected as the best alternative.
We asked military experts who have more than 10 years of experience in various military fields, including military policy, strategy, and operations to participate in this study, and 10 of them agreed to do so. A Delphi technique was utilized.
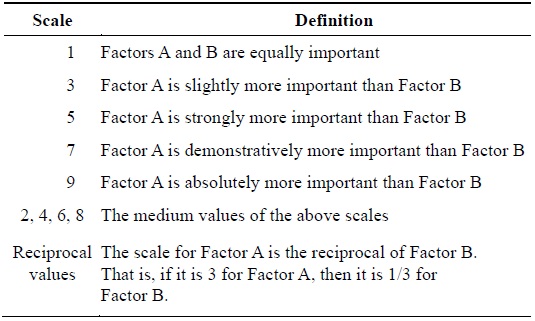
The survey instrument was designed on the basis of Saaty’s recommended range for comparison among factors (i.e., between 1/9 and 9) [9]. A ‘9’ indicates that one factor is
[Table 1.] Definition of scales used for pair-wise comparisons
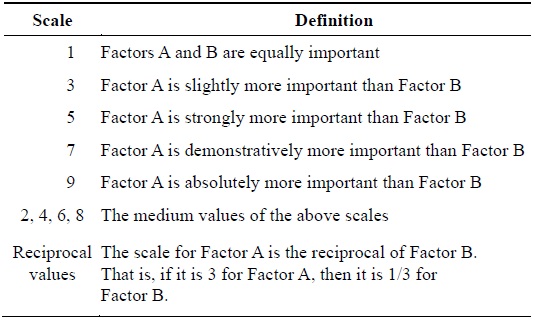
Definition of scales used for pair-wise comparisons
>
B. Application Procedures and Results
1) Application of DEA
In the first stage, we applied DEA to find an initial frontier group that satisfies all the necessary and optional conditions as discussed earlier. The input factors were price (including purchase and maintenance costs), fuel consumption, weapon carrying capacity, and durability; the output factors were capability (e.g., successful hit rate), take-off/landing distance, speed, engine thrust, and software performance. However, it is extremely difficult to quantify the input and output factors. The qualitative factors are also dominating factors. Therefore, a decision cannot be made by evaluating only the mechanical and technological factors. Therefore, the DEA method is good for finding an initial frontier group of fighter systems that can easily be adapted to the conditions in Korea.
For this study, we have used the efficiency and productivity analysis system (EnPAS) program. This program is particularly useful for our study because of the reasons [19]:
EnPAS identified three fighter systems as a frontier group: F-35A, F-15SE, and Euro-Fighter. Because of the sensitivity issues related to military decisions, we cannot discuss how many and what type of fighters were initially considered. The next step will be to prioritize the list to find the best fighter system. We applied a multi-attribute decisionmaking model called AHP to achieve this goal.
2) Application of AHP
Phase One: Hierarchy Formation
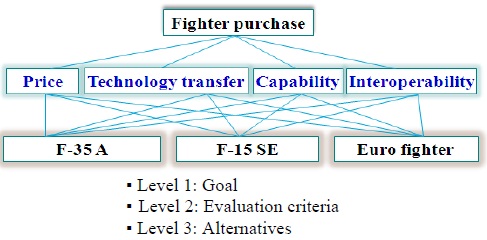
We formed a hierarchical structure as follows: the goal was to select the best fighter system. The evaluation criteria included price, technology transferability, capability, and interoperability with the existing fighters; and the alternatives were F-35A, F-15SE, and Euro-Fighter. Fig. 1 shows the hierarchy.
Phase Two: Pair-Wise Comparisons
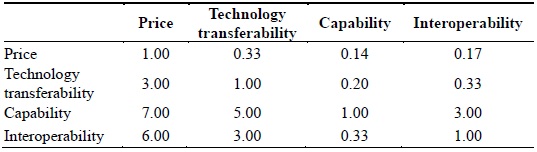
As discussed earlier, a series of pair-wise comparisons were carried out for the evaluation criteria and the alternatives. The results revealed that with respect to the evaluation criteria, the experts considered capability to be the most important followed by interoperability, technology transferability, and finally, price. With respect to alternatives, the relative priority showed that the experts considered F-35A, F-15SE, and Euro-Fighter. Table 2 summarizes the results.
[Table 2.] Results of pair-wise comparisons of evaluation criteria
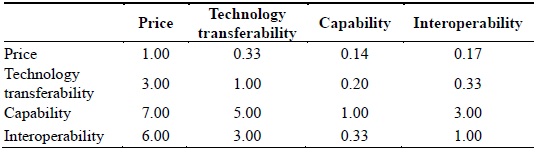
Results of pair-wise comparisons of evaluation criteria
Phase Three: Calculation of Weighted Value
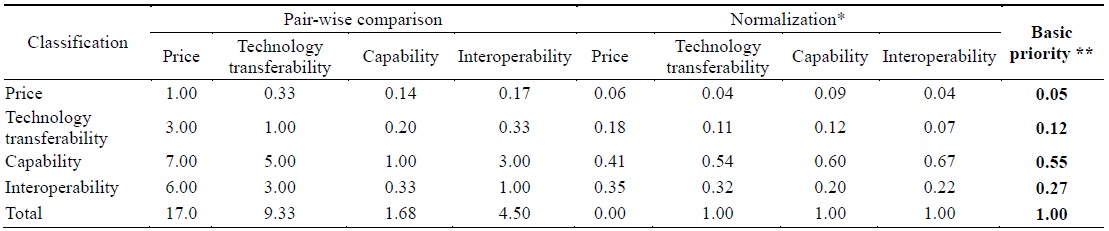
In this phase, we calculated the basic priority scores for each evaluation criterion and each fighter system after normalizing the data. Normalized values are calculated by dividing the value for each criterion by the total sum values for all the evaluation criteria. Basic priority is the arithmetic mean of the normalized values; that is, {(price + technology transferability + capability + interoperability) / 4}.
The results show that the basic priority scores are 0.05, 0.12, 0.55, and 0.27 for price, technology transferability, capability, and interoperability, respectively. This implies that the experts consider capability as the most important criterion followed by interoperability, technology transferability, and price. Table 3 summarizes the results.
[Table 3.] Weighted values of evaluation criteria
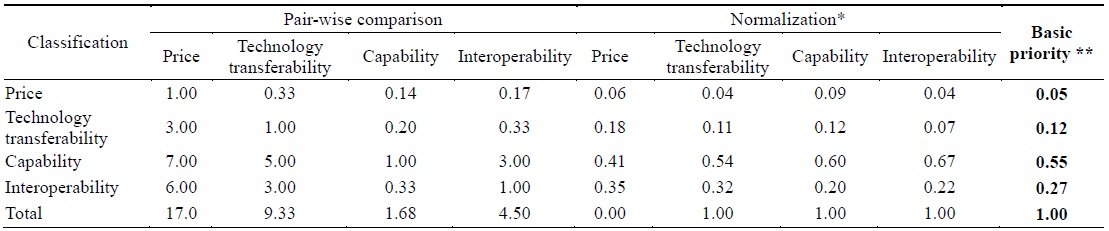
Weighted values of evaluation criteria
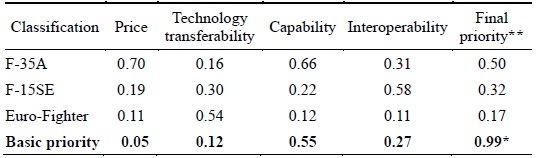
The next step calculates the priorities for the different fighter systems given the evaluation criteria. The results show the priority scores of 0.7, 0.19, and 0.11 for F-35A, F-15SE, and Euro-Fighter, respectively, for the price criterion. The Euro-Fighter, however, receives the best score for the technology transferability criterion: 0.16, 0.30, and 0.54 for F-35A, F-15SE, and Euro-Fighter, respectively.
In terms of capacity, as in the case of price, F-35A receives the highest priority followed by F-15SE, and finally Euro-Fighter: 0.66, 0.22, and 0.12, respectively. Finally, in terms of interoperability, F-15SE receives the highest priority followed by F-35A and the Euro-Fighter: 0.58, 0.31, and 0.11, respectively. Table 4 summarizes the results.
[Table 4a.] Priority scores for fighter systems for the price criterion

Priority scores for fighter systems for the price criterion
[Table 4b.] Priority scores for fighter systems with respect to technology transferability

Priority scores for fighter systems with respect to technology transferability
[Table 4c.] Priority scores for fighter systems with respect to capability

Priority scores for fighter systems with respect to capability
[Table 4d.] Priority scores for fighter systems with respect to interoperability

Priority scores for fighter systems with respect to interoperability
Phase Four: Consistency Evaluation
To check the consistency of the responses, we calculated both CI and CR on the basis of the formulas discussed earlier. The results showed that λmax = (4.27 + 3.92 + 4.20 + 4.12)/4 = 4.1275, and therefore, CI = (4.1275 - 4)/3 = 0.0425. The RI value, which was generated by a computer simulation based on non-consistent pair-wise comparisons, was 0.90, and CR was 0.0472 (0.0425/0.90). In sum, the participants’ judgments for the study could be considered consistent. Table 5 shows the calculations.
[Table 5a.] Consistency index calculation

Consistency index calculation
[Table 5b.] Computer-generated random index

Computer-generated random index
Phase Five: Selection of the Best Fighter System
The results show that the military experts in Korea consider F-35A to be the best fighter system followed by F-15SE and then, Euro-Fighter. This is consistent with the actual decision made by the Korean government. Table 6 summarizes the results.
[Table 6.] Final priority results for each fighter system
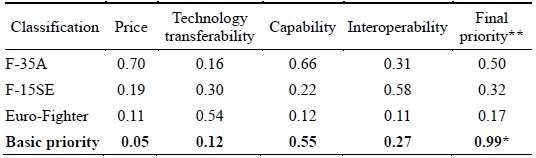
Final priority results for each fighter system
V. CONCLUSIONS AND IMPLICATIONS
In this paper, we propose a DEA-AHP integrated model that combines the merits of the two methods: efficiency assessment and priority determination based on weighted values. Since DEA does not pre-assign the weighted value, it can prevent falsifying results due to the subjective views of decision makers and/or uncertain weighted values. Further, the method can be applied to situations with various input and output factors since it can be done irrespective of the scales developed by using the evaluation factors.
The AHP method categorizes the evaluation criteria with different hierarchical structures; therefore, it is simple to develop an evaluation system logically [20]. This method can verify the consistency of the decision makers and develop a standardized and objective priority score system.
The results of the proposed DEA-AHP integrated method with respect to the selection of the next-generation fighter system in Korea show the usefulness of the method. However, its application is somewhat limited because the selection of a fighter system has to consider various scenario planning processes, such as contingency planning and future backward [21].
Contingency planning is often used for risk management when an unusual situation that, although unlikely, has catastrophic consequences. Such plans can be initiated either by the government or by the suppliers and can be preventative and/or corrective.
Future backward is a method of analyzing alternative futures, often environmental futures. Its major characteristics include working backward from a desired future set of goals to the present. It focuses on the feasibility of a particular future and the policy measures required to reach the goal.
In conclusion, the proposed DEA-AHP integrated model can be used at the practical and tactical levels, but a more comprehensive analysis such as the political, economic, social, technological, legal, and environmental (PESTLE) analysis should be used at the strategic level. The PESTLE analysis has been used in many disciplines including human resources management and marketing. The analysis is like an audit of an organization’s environmental influences to guide strategic decision making. To help make decisions and plans for the future, organizations need to understand not only the environment in which they operate and have limited influence or impact (meso-economic) but also the environment that includes all the factors that are out of the control of the organization but still influence the organization (macro-economic). By understanding these environments, the organizations can maximize their opportunities and minimize their threats [22].