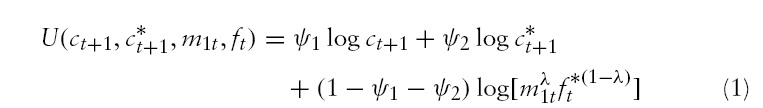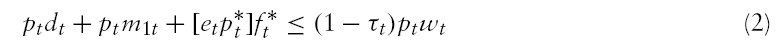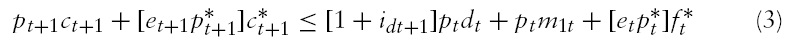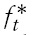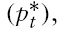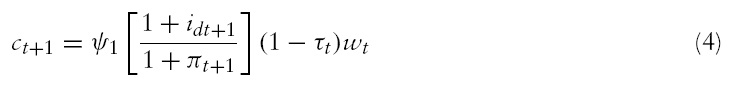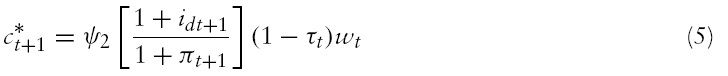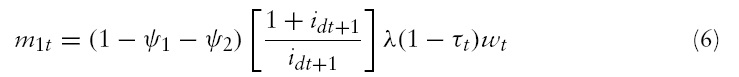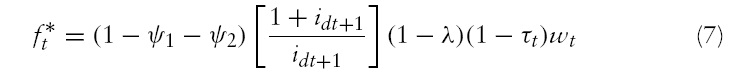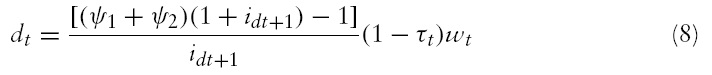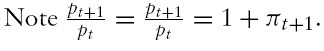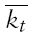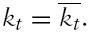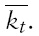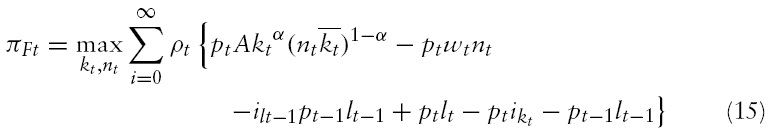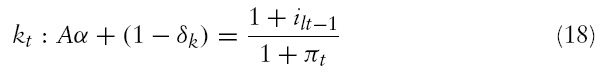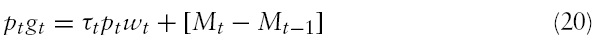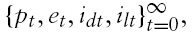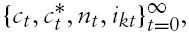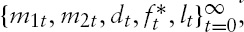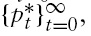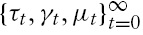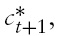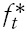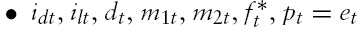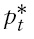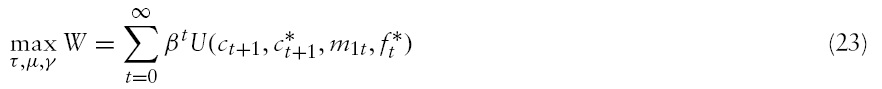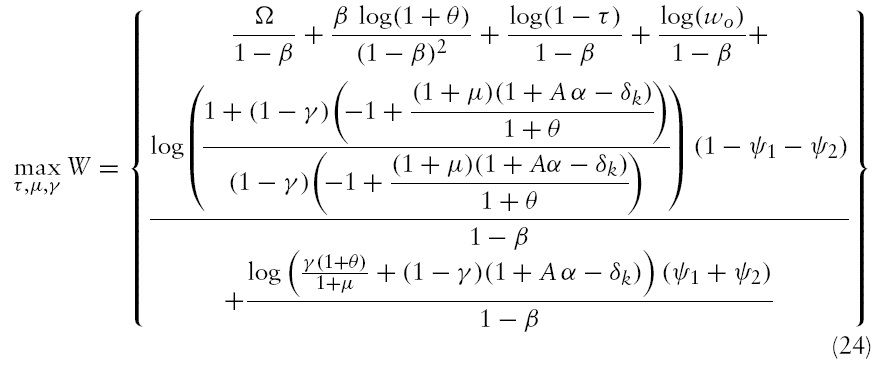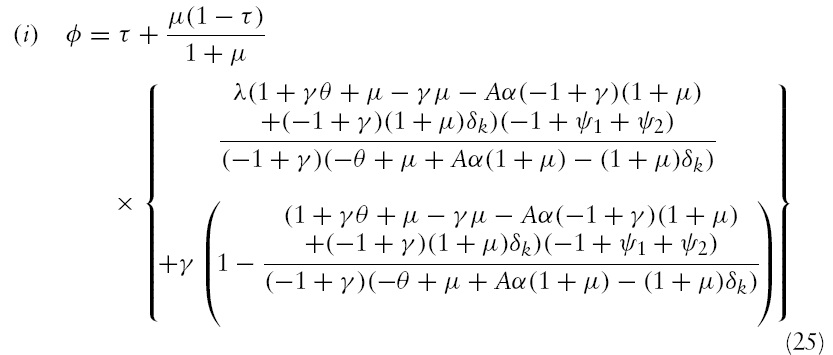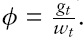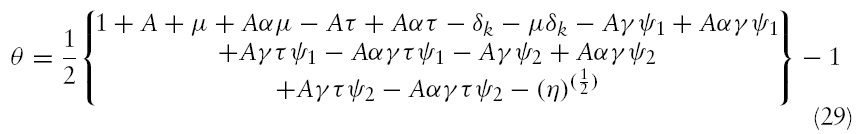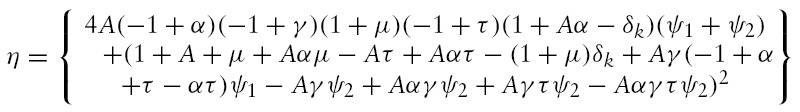Using a general equilibrium overlapping generations monetary endogenous growth model of a small open economy, we analyze the relationship between currency substitution and financial repression. We follow Drazen (1989), Bacchetta and Caminal (1992), Haslag and Hein (1995), Espinosa and Yip (1996), Haslag (1998), Haslag and Koo (1999), Bhattacharya and Haslag (2001), Gupta (2005, 2006, 2008) and Gupta and Ziramba(2008a, 2010a, 2009a, 2010b) amongst others, in defining financial repression through an obligatory ‘high’ reserve deposit ratio requirement, that the banks in the economy need to maintain. In other words, the study attempts to assay whether there exists a plausible explanation as to why the reserve requirements in some economies are higher than others. Specifically, we analyze whether the ‘high’ reserve requirements in a small open economy characterized by currency substitution, are a fall out of a welfare maximizing decision of the government, having access to income taxation and seigniorage as sources of revenue.
The motivation for believing that currency substitution can be a possible rationale for financial repression, can be outlined as follows: in a small open economy, inflation often leads to currency substitution, which, in turn, tends produce a negative impact on the revenue raised by the government via seigniorage. Against such a backdrop, our paper analyzes whether increasing the reserve requirements, our metric for financial repression, could be identified as an welfare-maximizing response of the government.This is simply because, the increase in reserve requirements would tend to recuperate the fall in the size of the seigniorage base that results from substitution of the domestic currency.
Note, financial repression can be broadly defined as a set of government legal restrictions, like interest rate ceilings, compulsory credit allocation and high reserve requirements, that generally prevent the financial intermediaries from functioning at their full capacity level. However, given the wave of interest rate deregulation in the 1980s, and removal credit ceiling some years earlier, the major form of financial repression is currently via obligatory reserve requirements.1 As Espinosa and Yip (1996) point out, the concern is notwhether financial repression is prevelent, but the associated degree to which an economy is repressed, since developed or developing economies both resort to such restrictive policies.
Now the pertinent question here is – why, if at all, would a government want to repress the financial system? This seems paradoxical, especially when one takes into account the well-documented importance of the financial intermediation process on economic activity, mainly via the finance-growth nexus.2 Besides the fact that ‘high’ cash reserve requirements enhances the size of the implicit tax base and, hence, is lucrative for the government to repress the financial system, alternative explanations, with varied success, have ranged from inefficient tax systems, in the form of tax evasion (Cukierman
In this regard, it is important to highlight a related recent paper by Holman and Neanidis (2006). These authors studied the growth and welfare effects of income tax and seigniorage in a small open economy characterized by currency substitution and and tax evasion. The paper indicates that seigniorage finance has stronger negative effects on growth relative to income taxation, when countries have less-developed financial markets. This result is reinforced for economies with a higher degree of currency substitution, greater substitutability of domestic currency via foreign currency and limited tax evasion. Finally, income taxation is found to be the least distortionary method of financing a given amount of government expenditures. Our study draws from this framework and analyzes the effect of an increase in the degree of currency substitution on financial repression in a welfare maximizing set up, with financial restriction being measured via the size of mandatory reserve requirements that the banks in the economy need to hold. Note, in the process, we have now allowed for an additional policy instrument, namely the reserve requirement, beside the income tax rate and the money growth rate, as used in their study. As well as modeling financial repression this way and trying to relate it to currency substitution, the decision to include cash-reserve ratio in the model is also data motivated. Based on the International Financial Statistics of the IMF, the average reserve requirement for the 22 economies considered by Holman and Neanidis (2006) was found to be 22.02% over the period of 1980 to 2006. Clearly, the ratio was quite substantial, and cannot be ignored as a monetary policy instrument.
Note, our results are difficult to compare directly with those of Holman and Neanidis (2006), not only because we are asking a different question, but also due to the fact that, in our case, the key monetary policy instrument measuring the degree of financial repression, namely the reserve requirement, is endogenous – unlike the exogenous measure of financial sector development used by Holman and Neanidis (2006). In addition, as will be seen below, currency substitution does not affect growth in our model and our constrained welfare maximization problem studies how the policy instruments would behave as the degree of currency substitution changes. Besides, our measure of welfare is quite different from that of Holman and Neanidis (2006) and in our case money is introduced via the money-in-the-utility (MIU) model rather than the cash-in-advance (CIA) constraint used by these authors. The remainder of the paper is organized as follows: section 2 outlines the economic environment and section 3 defines the equilibrium. Section 4 derives the conditions under which financial repression and currency substitution tends to be positively related as part of a welfaremaximizing outcome, while, section 5 concludes and lays out the areas of further research.
1See Caprio et al. (2001) for further details. 2See Roubini and Sala-i-Martin (1992), and the references cited there in.
In this section, the overlapping generations model of Diamond (1965) is modified to depict a financially repressed structure of a small open economy, characterized by currency substitution. The economy is populated by four types of agents, namely, consumers, banks (financial intermediaries), firms and an infinitelylived government. The following subsections lays out the economic environment in detail, by considering each of the agents separately and accounting for the external sector.
The economy is characterized by an infinite sequence of two-period- lived overlapping generations of consumers. Time is discrete and is indexed by
Each agent is endowed with one unit of working time (
Formally, the agents problem born in period
where
are the old age consumption of domestic and foreign goods, respectively;
and
is the domestic (foreign) price at period
The maximization problem of the consumer yields the following optimal choices:
We assume that the Purchasing Power Parity (PPP) condition,
At the start of each period, the financial intermediaries accept deposits and make their portfolio decision, i.e. loans and cash reserves choices, with a goal of maximizing profits. At the end of the period, they receive their interest income from the loans made and mees the interest obligations on the deposits. Note the intermediaries are constrained by legal requirements on the choice of their portfolio (i.e. reserve requirements), as well as by the feasibility requirement. Given such a structure, the intermediaries obtain the optimal choice for
s. to.
where
To gain some economic intuition on the role of reserve requirements, our metric for financial repression, let us consider the solution of the problem for a typical intermediary. Free entry drives profits to zero and we have:
Simplifying, in equilibrium, the following condition must hold
Reserve requirements, thus, tend to induce a wedge between the interest rate on savings and the lending rate for the financial intermediary.
All firms are identical and produce a single final good using a constant returns to scale, Cobb–Douglas-type, production function, given as follows:
where
denotes the aggregate capital stock in period
At time
The producers use the available bank loans,
Formally, the-firms face the following problem:
subject to
where
The upshot of the above static problem of the firmyields the following efficiency conditions:
Equation (18) suggests that the production firm sets its marginal product of the capital good equal to the real rental, while equation (19), simply states that the firm hires effective labor up to the point where the marginal product of labor equates the real wage. Note, we are using the fact that in equilibrium:
holds.
2.4 Government and the External Sector
In this subsection, we describe the activities of an infinitely-lived government. The government purchases
where
Finally, the balance of payments identity of this economy – assuming that (PPP), i.e.
where
has to be equal to zero. Without any loss of generality and maintaining consistency with perpetual growth, the exports of the economy,
3This assumption has no bearing on the results of our model. It makes computations easier and also seems to be a good approximation of the reality. For details see Hall (1988).
A valid perfect-foresight, competitive equilibrium for this economy is a sequence of prices
allocations
stocks of financial assets
exogenous sequences of
and policy variables
such that:
•Taking
such that equation (1) is maximized subject to equations (2) and (3).
•The stock of financial assets,
•The real allocations solve the firm’s date–
•The goods, money, loanable funds, labor and the bond market equilibrium conditions are satisfied for all
•The government budget, equation (20), is balanced on a period-by-period basis.
•The equilibrium condition in the external sector requires equation (22) to hold, along with the PPP condition being satisfied for all
and
must be positive for all
4. Currency Substitution and Optimal Policy Decisions
In this section, we analyze whether higher degree of currency substitution would result in an increase in the degree of financial repression within a specific country. In our case, this implies studyingwhether the optimal choice of the reserve-deposit ratio (
Using equations (4)–(8), (13), (16), (18) and (19), we obtain the following structure for the social planner’s problem:
subject to
where, Ω = log(
Further, using equation (18), we obtain
where
The problem of the social planner that comprises maximizing equation (24) subject to equations (25)–(28), is non-linear in
In this regard, it is important to point out that, as is often observed with monetary endogenous growth models in an overlapping generations framework, we obtained two steady-state growth paths.9 For our analysis, the negative root, as defined by equation (29), was chosen, since, for the given parameter values, while trying to match a growth rate of 2%, the positive root yielded a negative value for A, the production scalar. Hence, the positive root for
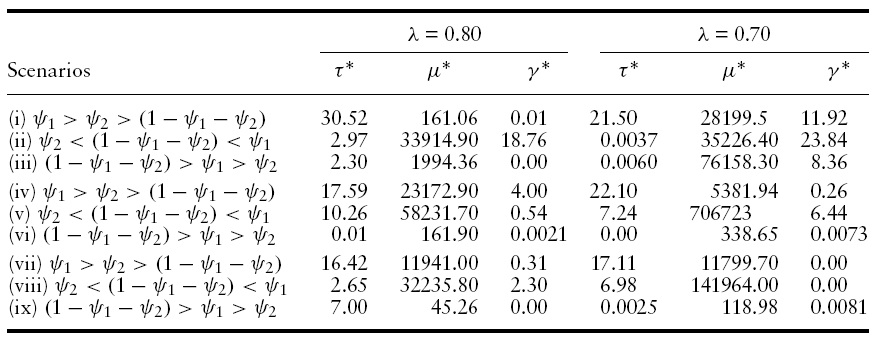
Columns 2, 3 and 4, and 5, 6 and 7 of Table 1 compares the optimal values of the tax-rate (
[Table 1.] Optimal policy decisions
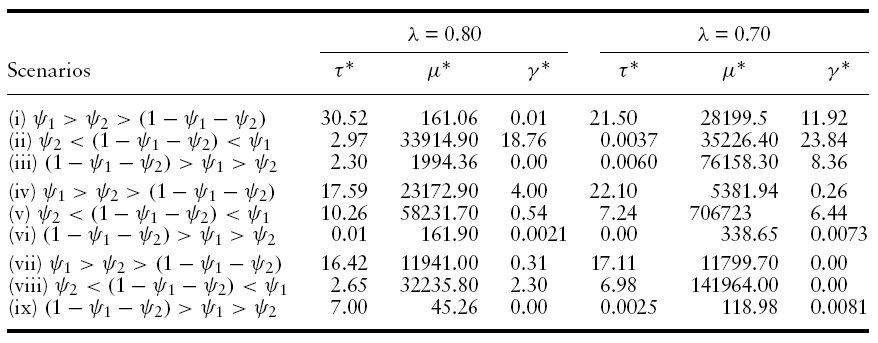
Optimal policy decisions
As can be seen from Columns 4 and 7 of Table 1, irrespective of the weight assigned by households on domestic consumption, foreign consumption and composite money, under scenarios (i), (ii) and (iii), higher currency substitution, always leads to higher optimal values of the reserve requirement. Moreover, in all these cases, the optimal tax rate falls while the optimal money growth rate increases. Two aspects of the results obtained need to be stressed: First, the optimal money growth rates, under the different situations, generally tend to be very high. However, such a result is not uncommon in monetary growth models based on an overlapping generations framework.10 Second, what is more important for our analysis, is the movements of the optimal policy parameters following changes in the degree of currency substitution, rather than their values per se. Intuitively, the results can be explained as follows: when the government size is relatively big, as under scenarios (i), (ii) and (iii), higher degree of currency substitution results in a fall in the size of the seigniorage tax base, via the money held by the consumers. The welfare maximizing government attempts to restore this reduction in the implicit tax base by increasing the reserve requirements and the money growth rate. With the real interest rate falling and reducing the welfare via the decline in domestic and foreign consumption and also through the fall in the growth rate, the welfare maximizing government reduces the tax rate to maintain growth and welfare. Note however, all these policy changes take place simultaneously to ensure that individual welfare is not only maximized but also that the government budget constraint holds.
To check for the robustness of our results,we decided to reduce the value of φ to 0.25, and then to 0.20, implying government-sizes of 15% and 12%, respectively. In the first case, we find that higher currency substitution now leads to higher financial repression in two of the three scenarios of the weights discussed above, i.e. for
So, as far as the relationship between currency substitution and financial repression is concerned, we can draw the following conclusions from the results obtained above.
• Higher currency substitution within a particular economy or across two similar economies (differing only in terms of the share of foreign currency in aggregate money), can cause higher degrees of financial repression.
• With larger government, irrespective of how the consumer values domestic and foreign goods and composite money, higher currency substitution always causes higher financial repression.
• With mid-sized governments, higher currency substitution can also cause higher financial repression, but nowthe consumer has to value composite money more than at least one kind of consumption good.
• With governments of relatively small sizes, higher currency substitution and reserve requirements are positively related only when the consumer puts more weight on composite money relative to both domestic and foreign goods.
• Finally, as in Holman and Neanidis (2006), under the comparable case of
4Note θ is independent of λ as the savings decision of the consumers, dt, is free of the currency substitution parameter. 5All the calculations were carried out using the NMaximize routine in Mathematica 5.0. 6The World Development Indicators (published by the World Bank), suggests that the per-capita world growth rate, in recent times, has tended to vary between 1.5% to 2.5%.We choose 2% simply as an average of this range. 7It must be pointed out that, for the sake of simplicity and without any loss of generality, we have converted the parameter values obtained from the five studies, mentioned above, to their nearest multiple of 5. As long as the framework is retained, the qualitative results of our analysis continues to hold irrespective of the values chosen for these parameters. 8Note this value of φ ensures a government-size of 20%, a figure widely encountered in the literature. See Bhattacharya and Haslag (2001) for further details. 9See Espinosa and Yip (1999) for further details. 10For example these were also obtained by Freeman (1987) and Gupta (2005, 2006, 2008) and Gupta and Ziramba (2008a, 2009, 2010b). Also refer to Bhattacharya and Haslag (2001) and Gupta and Ziramba (2008b) for a nice exposition as to how this issue can be handled.
5. Conclusions and Areas of Further Research
This paper, using a general equilibrium overlapping generations monetary endogenous growth model of a small open economy, analyzes the relationship between currency substitution and financial repression. Following other studies in the literature,we define financial repression through an obligatory ‘high’ reserve deposit ratio requirement, that the banks in the economy need to maintain. In other words, this study attempts to assay whether currency substitution can provide a rationale for financial repression. Specifically,we analyzewhether the ‘high’ reserve requirements in a small open economy characterized by currency substitution, are a fall out of a welfare maximizing decision of the government, having access to income taxation and seigniorage as sources of revenue.
We find that, higher currency substitution within a particular economy or across two similar economies, differing only in the degrees of currency substitution, can cause higher degrees of financial repression, with the results depending on the size of the government and what weights the consumer assigns to the domestic and foreign goods and the composite money. We find that the relatively large-size of the government is both necessary and sufficient to produce higher financial repression following an increase in the degree of currency substitution. For middle-sized government, sufficiency requires the consumer to value composite money more than at least one kind of consumption good, while with smaller-sized government, currency substitution and financial repression are positively correlated only when the consumer puts more emphasis on the composite money than consumption of domestic and foreign goods.
A limitation of the existing study, as in Holman and Neanidis (2006), is that it does not endogenize currency substitution.11 The fact that currency substitution mainly arises due to high inflation, and hence should be ideally treated as endogenous, has been ignored in this study. In our economic model, it is as if high and continuous inflation episodes have resulted in a certain steady-state level of currency substitution for the economy, and, hence, the same can be treated as exogenous.Moreover, endogenizing currency substitutionwould not have allowed us to carry out the existing analysis of optimal policy responses, following a change in the share of the foreign currency in aggregate money. Once currency substitution is endogenized,wewould, in turn, have to analyze the optimal policy changes following variations in the structural parameters determining the steadystate level of currency substitution, originating from possibly high money growth rates. But then, in a welfare maximizing set-up with a government responding to higher degrees of currency substitution resulting fromhigher money growth rates, it would amount to the government not being able to use money growth rate as an instrument, simply because further changes in the money growth rate would now cause the degree of currency substitution to change again. So, in the context of our current economic environment, the government will now be left with only the reserve requirements and tax rates as its policy instruments.Nevertheless, this could be an interesting extension.
11Gupta (2008) and Gupta and Ziramba (2009) raise similar concerns about studies treating tax evasion as exogenous and analyzing optimal responses of government policies following changes in the exogenous degree of tax evasion.