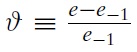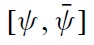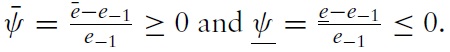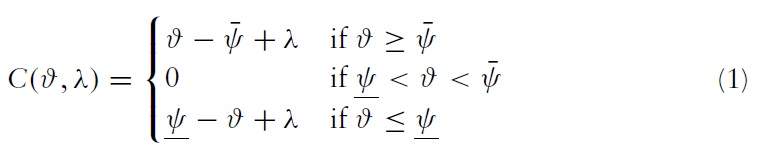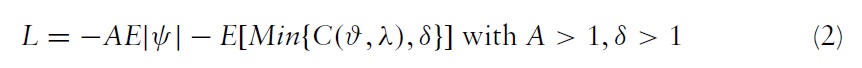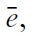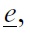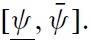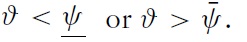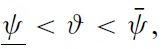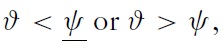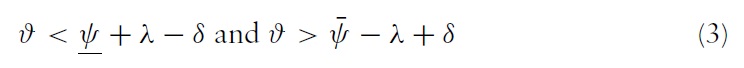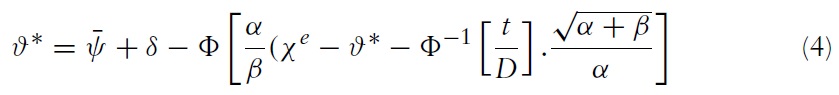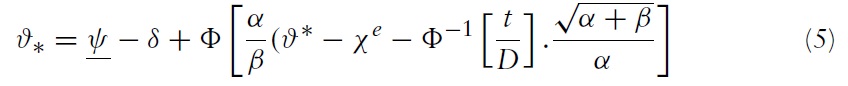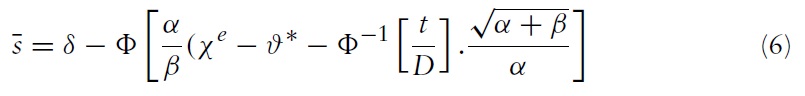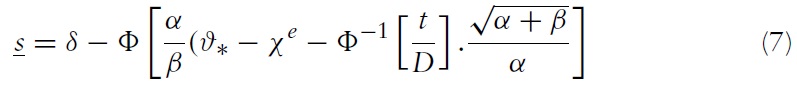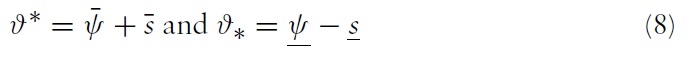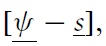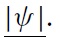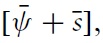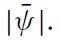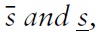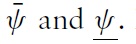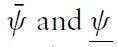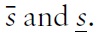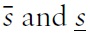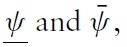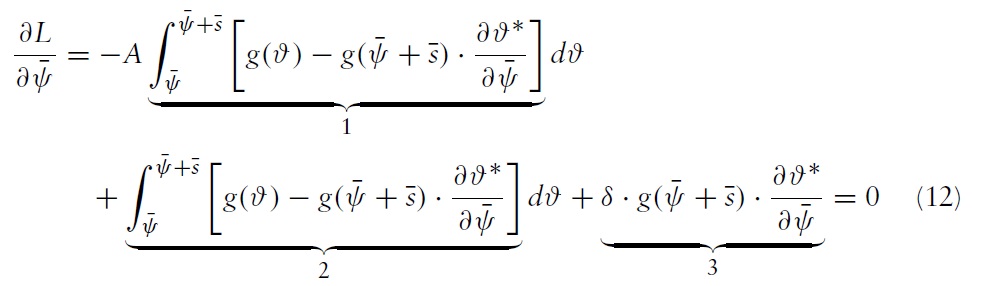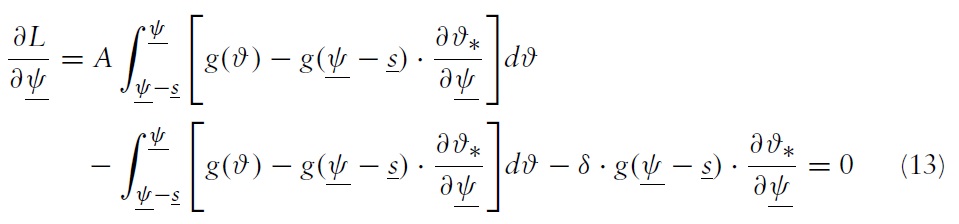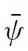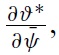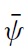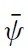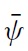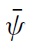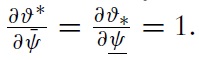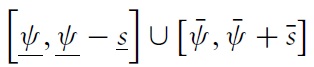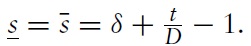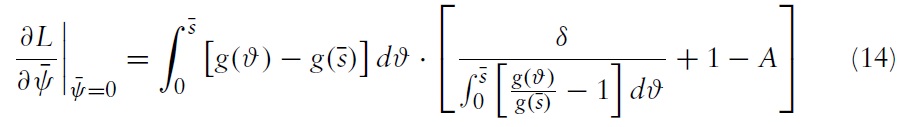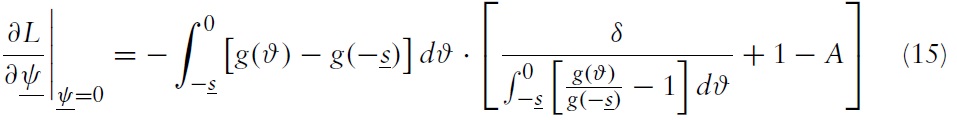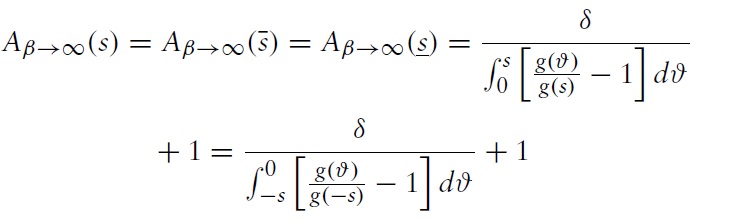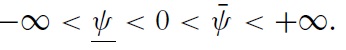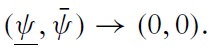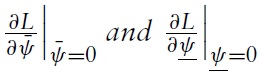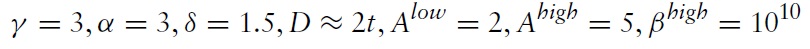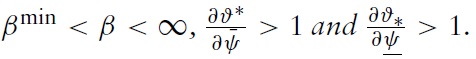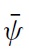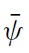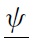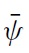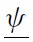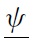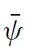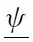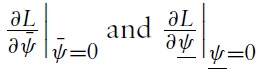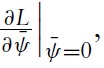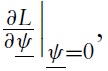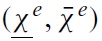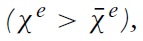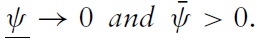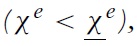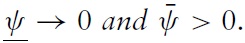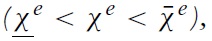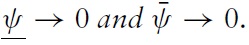Developing countries often face the problem of self-fulfilling behaviour on the part of international investors. Either they are too optimistic or too pessimistic, the result being harmful for the country. Indeed, periods of excessive optimism often breed their reversal. Faced with this unstable environment, an important issue for policymakers is the choice of exchange-rate policy. Specifically, what is the best exchange-rate policy that will ensure exchange-rate stability? Should the exchange rate be firmly fixed like irreversible pegs, be softly managed, or be allowed to float freely?

Obviously, choosing the right exchange-rate policy requires a better understanding of self-fulfilling crises, while most traditional crisis models (Obstfeld, 1996; Jeanne & Masson, 2000) , characterised by multiple equilibria, suggest that such speculative events are hardly predictable because they are related to extra-economic variables, such as sunspots. A more recent series of papers argues that the one of the main factors affecting the likelihood of self-fulfilling crises is the country’s level of transparency. From a theoretical point of view (Morris & Shin, 1998, 2000; Metz, 2001), transparency, measured by the precision of private information about the true economic state, is a key parameter. Accordingly, speculators’ expectations depend critically on parameters that either strengthen or dampen beliefs of each speculator on the other speculators’ decision to attack. In turn, such decisions determine the sustainability of an exchange-rate regime and the stability of exchange rates. Many empirical studies also reach such conclusions (Bannier, 2006;  Gelos & Wei, 2002; Mehrez & Kaufman, 2001; Wei, 2001; Johnson et al., 2000).

However,when thinking about exchange-rate regimes, academics tend to ignore informational aspects of such crises in twoways. First, they take it for granted that transparency is a virtue and dismiss any system that does not maximise the clarity of information.However, according to the last International Transparency Report (Transparency International, 2008), economic transparency is far from perfect in many countries. Second, economists tend to neglect the fundamental role played by international rating agencies in shaping expectations. As shown by Reisen and Von Maltzan (1999) or Reinhart (2002), international investors are often inclined to use informational signals sent by international rating agencies, which are often suspected to either over-valuate or under-valuate the economic perspectives of a country. Here, for the first time, both aspects are taken into account in a model of exchange-rate policy design.

To date, only one paper has proposed a theoretical model dealing with the choice of exchange-rate policy in an economy vulnerable to self-fulfilling crises. This is the framework of Cukierman et al. (2002). hereafter CGS. The present paper expands on this model. Both papers make use of Morris and Shin’s (1998, 2000) framework to model self-fulfilling attacks. Based on a global games approach, first introduced by Carlsson and Van Damme (1993), Morris and Shin show that indeterminacy of multiple equilibria, induced by the common knowledge of fundamentals assumption, can be removed once small uncertainty about the true fundamentals is introduced. By using this environment, it is possible to find a unique solution to the likelihood of self-fulfilling crisis and to relate it to the choice of exchange-rate regime.

Cukiermann et al. (2002, 2004) emphasised that there are some strategic interactions between the choice of exchange-rate regimes and the probability of self-fulfilling crises. This, in turn, allows interesting policy prescriptions. Nevertheless, the whole paper is based on the assumption that information on fundamentals is almost perfect. However, byworking with the limiting casewhere information is extremely precise, they neglect the problems raised by the lack of transparency in many countries. Here, a generalised version of their framework is proposed by relaxing the assumption of full transparency and by adding a new source of information sent by international rating agencies.

The results suggest that the stabilisation properties of an exchange-rate regime critically depend on the degree of transparency of the country. Furthermore, stabilisation properties of the regime are conditional on conjectural and time-varying factors, such as market sentiments, which swing according to rating agencies’ feelings. Paradoxically, in a weakly transparent economy, greater flexibility is found – in some circumstances – to create a wide range of exchange rate stability compared with hard-anchoring regimes. At the root of this outcome is the idea that in non-transparent countries, during stressful situations, international investors are more prone to anchor their expectations on public news and information (such as ratings, announcements of difficulties in big banks, sells from a large hedge fund, etc). Hence, much effort will be devoted to defending an institutional fixed-peg value, which is in any case neglected by investors.

The remainder of the paper is structured as follows. The model is presented in the next section, and the unique equilibrium is determined in Section 3. Section 4 characterises the optimal exchange-rate regime and identifies conditions under which it is a soft peg or a hard peg. Simulations are used to gain insight on the equilibrium properties.Adiscussion of the results follows in Section 5, afterwhich we conclude.

The present model is closely related to that of CGS (2002). It deals with the strategic interaction between the government and a group of atomistic speculators normalised to 1. The initial level of the nominal exchange rate is denoted e₋₁ and the free-float exchange rate that would prevail in the absence of policy interventions and speculation is denoted e. For convenience, the fundamental variation of the nominal exchange rate

is used and it reflects, for instance, the shocks of the current account or the trade balance.1

Assumption 1 The value of ϑ is assumed to be drawn froma normal distribution g(ϑ), (with G[.] the cumulated distribution) around a mean of 0 and a variance of 1/γ . Therefore, large fundamental shocks are less likely than smaller ones.

The policymaker internalises the idea that private agents dislike nominal exchange rate instability. Exchange rate instability does indeed reduce the incentives to trade assets and goods.2 Therefore, before any fundamental random shocks, i.e. exante, the policymaker sets an exchange-rate band,

around an initial level e₋₁. Thus, the degree of flexibility of the regime is directly related to the boundaries of the band of fluctuation,

The model studies only two kinds of explicit exchange-rate policies: hard pegs allowing no fluctuations and soft pegs allowing large fluctuations. Thus, the degree of flexibility of the regime refers to the softness of the peg.3 The pre-commitment policy incurs a cost. This cost is either a cost of defence or a cost of abandonment. The cost of defence depends not only on the fundamental shocks but also on the proportion of attackers, denoted λ. More specifically, the cost of maintaining the band increases with the degree of disequilibrium that the policymaker tries to maintain and the proportion of attackers. If this cost is too high with respect to the loss of credibility in case of abandonment, the government will choose to escape in spite of pre-commitment.

The cost of intervention to save the chosen band is:

The trade-off between minimising exchange rate instability and minimising the cost of adopting a band is formalised by postulating the following objective function:

where A is the degree of aversion to exchange-rate instability, ψ the actual rate of change in the nominal exchange rate and δ the present value of loss in terms of credibility if the government exits the band.

2.2.1 Information structure

Speculators use two kinds of information. First, before fundamental shocks occur, all speculators are supposed to exploit a common and public source of information, shared by everyone. This information is supposed to be sent by international rating agencies, which benefit from a high level of publicity in the financial marketplace. The main motive behind these assumptions is the increasing role played by international rating agencies. While these economic players sometimes focus on the wrong variables and tend to over-valuate or under-valuate a country’s potential, speculators still seem to use information sent by them. This element is clearly absent in the CGS model.

Assumption 2 All speculators exploit ex-ante a common public signal, χ^e, called the market sentiment.This signal is produced and sent by rating agencies. Ex-ante, speculators are supposed to believe that the economic fundamentals are normally distributed around χ^e with precision α > 0.

The signal χ^e is public in the sense that it is common knowledge and reflects the common financial market sentiment about economic performance. Formally, this common public signal refers to the prior information of speculators while the parameter α might measure the level of confidence in rating agencies.

Second, when fundamental shocks occur, all speculators cannot observe the true fundamental variation. Instead, they receive a private signal.

Assumption 3 Each speculator independently observes a noisy signal of fundamentals that would prevail under free-float. They individually receive a private signal χ_i = ϑ + ε_i. Noise terms are assumed to be random and subject to independent normal distributions with E(ε_i) = 0 and Var(ε_i) = 1/β and E(ε_iϑ) = 0.

The parameter β measures the degree of transparency of the economy. The higher β, the more reliable private signals turn out to be and the better private agents can infer the true effective fundamental variation.4 Moreover, the higher the value of β, the easier each speculator can guess the signals received by opponents. This assumption clearly differs from the CGS model, which considers almost full transparency with noise uniformly distributed around 0.

2.2.2 Speculator decisions

After receiving signals, each speculator has to decidewhether to attack the regime or not. Speculator i can attack the upper bound by borrowing the foreign currency at current low price,

and then selling it for domestic currency. The cost of the transaction is denoted t. The speculator’s net payoff is equal to the constant value D − t > 0 if the policymaker exits the upper bound. In contrast, if the policymaker successfully defends the band, the speculative attack fails and the net payoff of the speculator is −t < 0. The net payoff of not attacking is assumed to be equal to zero. Likewise, each speculator i can attack the lower bound of the band by borrowing the domestic currency at current low price,

and then selling it for foreign currency. The structure of payoffs is similar to the previous case.

The sequence of events unfolds as follows.

• At Stage 1, before any fundamental realisation, the policymaker announces a band of fluctuation

The policymaker commits to intervene and to stabilise the variations of the exchange ratewhenever it reaches the level

• At stage 2, the free-float random shock occurs. There are two possible cases:

(1) If

the nominal exchange rate is determined by market forces. Hence, the exchange rate adjusts to its natural value and gains through speculation are impossible.

(2) If

the exchange rate adjusts to the lower or upper bound of the band. Gains through speculation are possible. Simultaneously, speculator i gets the signal on ϑ and decides whether or not to attack the band. This decision determines the fraction, λ, of speculators who decide to attack the band.

• At stage 3, the policymaker observes the true value of ϑ and λ, evaluates the total cost of defending the band and chooses whether or not to defend the regime for the future.

1We recognize that in the real world, exchange rates may be disconnected from their underlying fundamentals. Moreover, from a theoretical point of view, since the seminal work by Meese and Rogoff (1983), the dynamics of exchange rates are often described as a random-walk process. Nevertheless, in the medium or long run, the fundamental view can beat the random walk (Gourinchas & Rey, 2007). Thus, we focus on this term and consider that exchange rate cannot disconnect too much from its fundamental or equilibrium value.  2Further arguments are presented by Calvo and Reinhart (2002).  3Obviously, the regime of pure floating exchange rates chosen ex-ante by the government is not considered in this model. As developing countries need external funds to grow, a basic level of guaranteed currency stability is required.  4Signalsmay be private in the sense that, among speculators, there are small discrepancies in howone observation is interpreted. The more transparent economic activities are, the less the interpretations of the same signal differ.

The model will be solved backwards. Given the exchange rate regime and the proportion of attackers, the policymaker will continue to defend its currency band if C(ϑ,λ) < δ. Thus, the set of fundamentals for which the policymaker will abandon the regime is:

The uniqueness of equilibrium in models of self-fulfilling currency attack represents the most important result found by Morris and Shin (1998, 2000).5 In our context, the equilibrium of the game consists of a unique strategy for the government and a unique strategy for speculators such that no player has an incentive to deviate. The equilibrium strategies are characterised by two pairs of equilibrium values, (ϑ_∗, χ_∗) and (ϑ ^∗, χ^∗), which belong to two situations of indifference:

(1) For the fundamental threshold ϑ = ϑ ^∗ [ϑ = ϑ_∗], the policymaker is undecided as to abandon the upper [lower] bound of the fluctuation band or continue to defend it. For all ϑ > ϑ^∗, [ϑ < ϑ_∗] the policymaker gives up the upper [lower] bound.

(2) The marginal speculator, receiving the threshold signalχ = χ ^∗ [χ = χ_∗] is undecided as to attack or to refrain from doing so. All speculators receiving a signal χ > χ^∗ [χ < χ^∗] decide to attack.

Under sufficient conditions for uniqueness,6 the following equations are obtained:

and

are defined as follows:

and

Equations (4) and (5) are rewritten:

Proposition 1 The chosen exchange-rate regime

gives rise to a range of effective stability (RES):

When ϑ falls inside

the policymaker defends the currency and ensures that the rate of depreciation is not greater than

When ϑ falls inside

the policymaker defends the currency and ensures that the rate of appreciation is not greater than

When ϑ falls outside the range of effective stability, the policymaker lets the exchange rate float freely in accordance with market forces.

Proposition 2 The range of stability is a compound of two sub-ranges of stability,

whose widths depend on the chosen regime.

As in the CGS model, the fundamental threshold of crises ϑ^∗ and ϑ_∗ depends directly on the chosen regime through

However, unlike CGS, we can also see that the fundamental thresholds of crises ϑ^∗ and ϑ_∗ depend indirectly on

through the terms

This is one of the most important differences to the

model, in which

depend only on exogenous parameters.

Corollary 1 The likelihood of crisis equals: P = G[ϑ_∗] + [1 − G[ϑ^∗]].

At this level, it can be inferred that the stabilisation virtues of the exchangerate regime are intrinsically measured by the likelihood of the RES

Thus, the properties of this zone are crucial to determining an optimal exchange-rate regime.

5Traditional models of self-fulfilling crises, based on the assumption of common knowledge of fundamentals, leads to multiple equilibria. The problem with the common knowledge assumption and multiple equilibria is that the onset of an attack appears to be arbitrary. Indeed, a sudden shift in confidence, caused by some extra-economic variables, such as sunspots, can trigger an attack, since all speculators receive the same information and behave in the same way. Speculative attacks may be triggered even though everyone knows that fundamentals are sound, and there is a continuum of equilibria with self-fulfilling beliefs. Instead,when agents get noisy signals on the state of fundamentals, common knowledge no longer holds. Paradoxically, according to Heinemann and Illing (2002), this property, rather than worsening themultiplicity problem, is sufficient to eliminate it. Indeed, there is no longer a correlating device on which agents can coordinate their actions. Even if market participants are well informed about the economic situation, they are unsure of the information received by other participants. Hence, the success of an attack becomes uncertain to them. Agents must compare potential gains and losses from success or failure of a speculative attack.This calculation imposes a newequilibrium condition that eliminates all but one equilibrium (Heinemann, 2000).  6It can be easily shown that this condition reduces to

Assuming that the conditions for uniqueness are guaranteed, the policymaker’s objective function will now be treated. The expected variation of the exchange rate is:

The expected payoff of the policymaker, given

is:

The policymaker chooses the boundaries of the band so as to maximise the expected payoff. The first-order conditions for interior solutions to the policymaker’s problem are:

After some rearrangement, the following equations are obtained:

and

Equations (12) and (13) show that by altering the boundaries of the band, the government moves along a trade-off between exchange-rate stability induced by a regime and the costs induced by that regime. In what follows, the different terms of equation (12) are detailed, keeping in mind that similar comments hold for the terms in equation (13).

The first term weighted by −A measures the marginal effect of an increase in

on exchange-rate stabilisation.Within the CGS model, any RES is constant in width and large shocks are less likely than smaller ones. Thus, without ambiguity, this effect turns out to be negative: more flexibility means less effective stability. In the present model, the sign of this effect becomes more ambiguous. A new element, formally introduced by

may balance this negative mechanism. As shown in Section 4.3, this term is strictly greater than unity when the assumption of full transparency is relaxed.This termmeasureswhat is called the coordination effect, not present in the CGS model. Coordination mechanisms stem from the fact that now any RES may widen whenever

increases, thereby reducing the likelihood of crisis and increasing stability. The intuition of this effect is given in Section 4.3. The second term represents the marginal effect of raising

on the cost of defending the regime. It can be either positive or negative. In contrast, the third term is always positive, because increasing

lowers the likelihood that the exchange rate will move outside the RES and lead to realignment.

4.1.1 Optimal Choice in a Very Transparent Economy

In this subsection, a specific case is given where private agents get very precise information on the true value of fundamentals. Suppose that the degree of transparency is extremely high and ‘β’ goes to infinity,7 we get the following Lemmas.

Lemma 1 An increase in

generates a proportional increase in ϑ^∗ and a decrease in

generates a proportional decrease of ϑ_∗. Indeed,

Moreover, the range of effective stability

does not depend on the chosen regime. In this case, we have

Lemma 2 As large shocks are less likely than smaller ones, the efficiency of the RES decreases when

increases in absolute value.

The first-order condition can be simplified as follows:8

and

By assuming

the following is obtained.

Proposition 3 (a)

then the optimal regime is a band of fluctuation with

(b) If

then the optimal regime is a fixed peg with

These findings are well illustrated by the simulation shown in Figure 1. The sign and the value of

provide a proxy of the desirable degree of flexibility. These simulations are robust to the choice of parameter values, with some exceptions. Typically, for simultaneously extremely high ‘δ’ and ‘A’, these results do not hold anymore.The simulationswere performed using Mathematica 4 software with the following parameter values:

In this section, the assumption of high transparency is relaxed. The following lemmas give the new properties of any RES.

Lemma 3 When

In other words, a rise in

increases the upper fundamental crisis threshold ϑ^∗ more than proportionally and a decrease in

decreases the lower fundamental crisis threshold, ϑ_∗ more than proportionally. This means that the width of the RES now depends on the chosen band. In a non-transparent environment, the impact of an increase in

or a decrease in

is magnified by a coordination effect,which leads to wider RES.Thus, the likelihood of the RES does not decrease systematically when

is raised or when

is lowered.

This result suggests that a soft-peg commitment may be more effective in terms of stabilisation than a hard one. At this level, the relevant question to address is the following: in which case does the band of fluctuation produce stabilisations that perform well enough to represent a good alternative to hard-anchoring regimes?

Intuitively, final outcomes will depend on the relative magnitude of two effects: a conventional effect and a coordination effect.The conventional effect, also highlighted in the CGS model, links the efficiency of any constant range of effective stability (RES) to the likelihood of fundamental shocks. As in the CGS model, this turns out to have a negative effect on exchange-rate stabilisation. Since large shocks are less likely than smaller ones, the efficiency of any constant-width RES decreases when

or

increases in absolute value. The second effect, the coordination effect, not present in the CGS model, stems from the fact that the width of RES is no longer constant. The RES may widen whenever

or

increases in absolute value. In other words, the efficiency of the RES does not decrease systematically when the policymaker announces a more flexible peg. In a context of non-transparency, what matters is the role played by higher-order beliefs of some participants who are apprehensive about others’ beliefs on the beliefs of yet other individuals. Faced with the announcement of a more flexible peg, each speculator considers that all other speculators will be less aggressive. More importantly, each speculator considers the fact that other speculators consider that all other speculators will be less aggressive. This higher-order belief leads to a coordination effect that may surprisingly improve exchange-rate stability when more flexibility is announced. An additional element adds to the complexity of this mechanism. Themagnitude of this virtuous coordination effect also depends on the role played by rating agencies. As a public signal, the market sentiment sent by rating agencies may serve as a coordinating device (Boot et al., 2006) and determines the likelihood of self-fulfilling crises as well. The flexible peg may be even more stabilising when rating agencies are influent and when market sentiments are extreme.

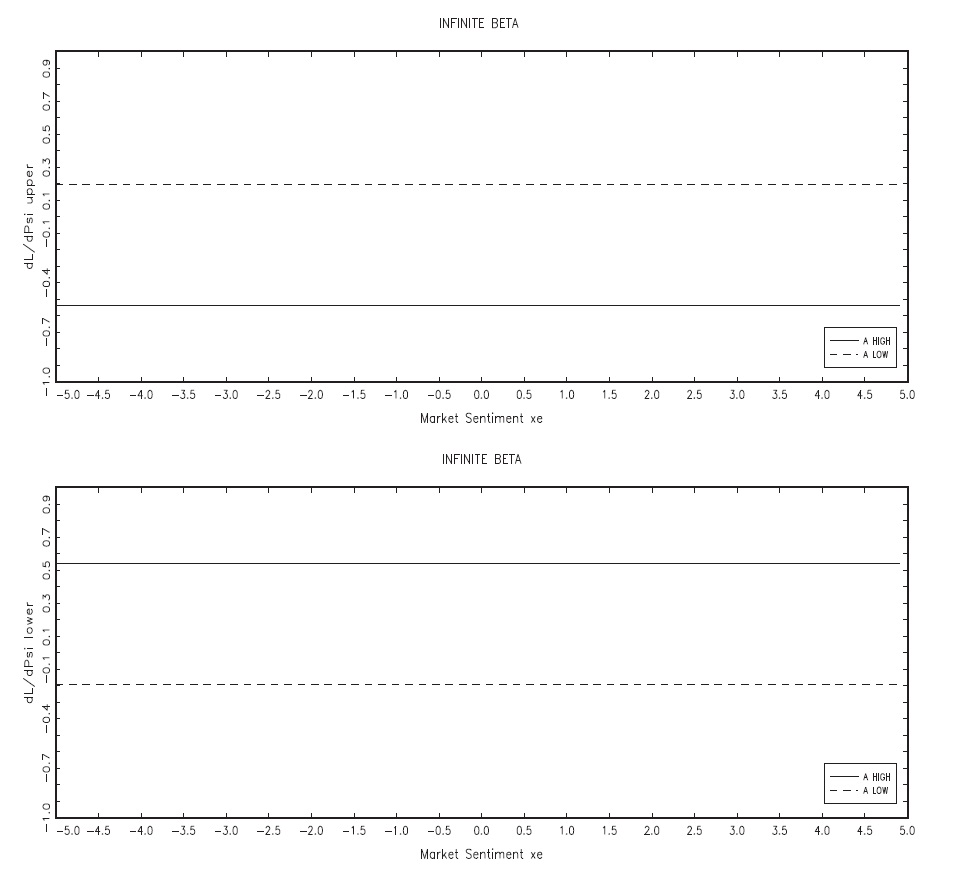
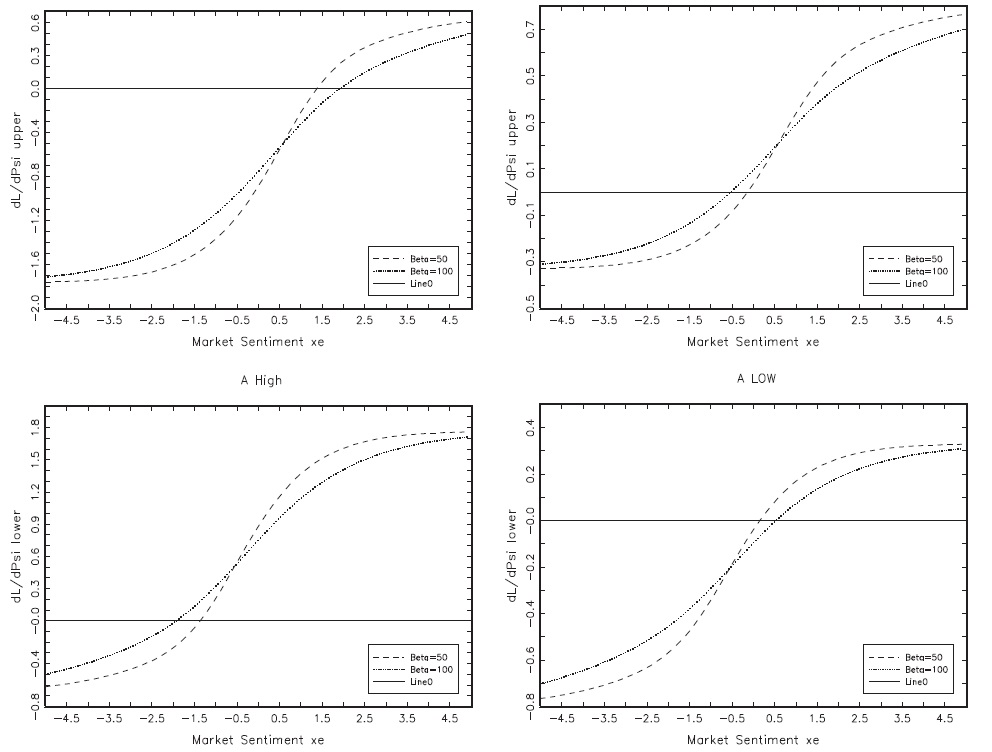
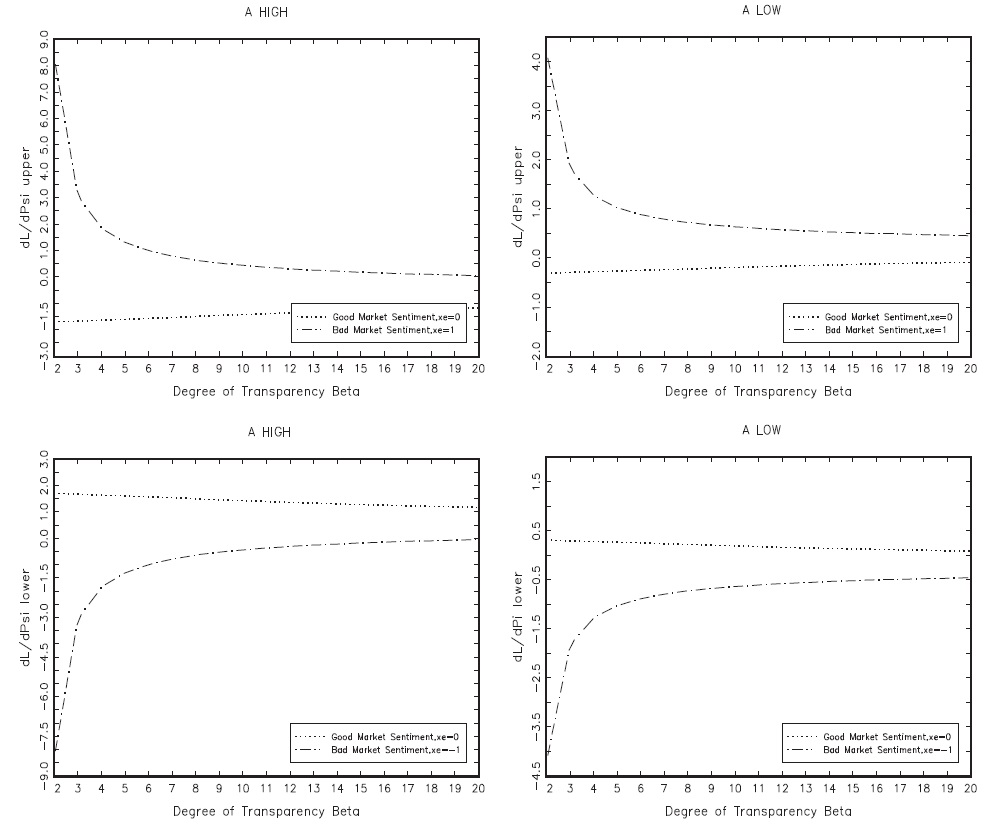
As explained above, in regards to the complexity of the model and equations for defining the optimal solution, some simulations were performed and the values of

were plotted. The higher the value of

the higher the desirable degree of flexibility of the upper bound. Symmetrically, the lower the value of

the higher the desirable degree of flexibility of the lower bound. Observations from Figures 2 and 3 are summarised in Tables 1 (a), (b) and 2, respectively. The most interesting case is illustrated, i.e. when the aversion to exchange-rate instability is high.When aversion to exchange rate instability is low, the choice for flexibility is obvious, in that soft pegs are systematically preferred over hard pegs.

The optimal exchange-rate policy has particularly interesting characteristics. In what follows,

represent critical values of market sentiment.

Proposition 4 When the market sentiment is high,

the optimal currency band is asymmetric,

The lower the degree of transparency, the higher the desirable degree of flexibility of the upper bound.

Proposition 5 When the market sentiment is low,

the optimal currency band is asymmetric,

The lower the degree of transparency, the higher the desirable degree of flexibility of the lower bound.

Proposition 6 When the market sentiment is moderate,

a zerowidth band is more desirable, with

Proposition 7 When the market sentiment can switch from high optimism to high pessimism,

the currency band tends to a near-symmetric band. The optimal currency band is even wider when the degree of transparency is low.

Corollary 2 When the degree of transparency of an economy is not perfect, the optimal decision depends on the market sentiment.

7It is assumed that α is neither extremely high nor extremely low.  8As the functions are respectively equal to zero in the decision rule is quite simple. If is positive around that means that the policymaker should shift above zero and if is negative around he should push all the way up to zero. The same reasoning applies for the lower bound.

The optimality of exchange-rate policies is shown to depend on the degree of transparency of a country.

In highly transparent economies, the optimal choice of the policymaker depends mainly on the aversion to exchange-rate instability. In this context, all speculators get a very precise signal on the true fundamental exchange-rate variation. Thus, they give almost no weight to the informational content of the public signal sent by international rating agencies. Furthermore, each speculator assumes that all other speculators will base their actions solely on their private signals, which are practically the same for everyone. Everything happens as if they do not need to anticipate others’ strategies. The announcement of a soft peg informs speculators that the set of fundamentals for which the attack is a success becomes narrower and the likelihood of a successful attack decreases via a simple ‘fundamental’ effect. This is why the aversion to exchange-rate stability is so important in the trade-off between exchange-rate instability and the cost of defending a harder peg.

In contrast, when the degree of transparency is low, each speculator must infer the true fundamental value as well as others’ strategies. The relative importance of public signals sent by rating agencies being even more important when transparency is low, speculators will give more and more weight to the informational content of public signals in calculating the expected value of fundamentals. However, even more important is the fact that public signals indirectly informindividual speculators of others’ intentions to carry out a speculative attack. Thus, a very public signal that fundamentals may vary even a small amount may have a large impact on the likelihood of self-fulfilling attacks. All else being equal, when public sentiment is very high or very low, the likelihood of a crisis in a nontransparent environment is higher than in a very transparent one. In this context of high expected distress, the effect of the exchange-rate policy on the likelihood of a crisis reaches its maximal level. In other words, a soft peg allowing even the smallest of fluctuations may paradoxically strongly improve exchange-rate stability because, now, each speculator considers that all other speculators will be less aggressive. This is true to the extent that, when the market sentiment frequently switches from high optimism to high pessimism, the sub-optimal character of hard regimes characterised by (π, π) → (0, 0) is even more important when the level of transparency is low. It can also be argued that, during a stressful situation in non-transparent countries, international investors are more prone to anchor their expectations on public news and information (such as ratings, announcements of difficulties in big banks, sells from a large hedge funds, etc). Hence, much effort will be devoted to defend an institutional fixed-peg value, which is in any case neglected by investors.

Overall, this paper highlights the detrimental effect of hard regimes, such as dollarisation or hard pegs, in poorly transparent economies. It has been shown that, by neglecting the so-called coordination effect, policymakers tend to underestimate the stabilisation virtues of more flexible programs. Notably, this is precisely when expectation anchoring is most necessary, i.e. when market sentiment is high in absolute value, that the stability properties from hard regimes are lower than the ones induced by flexible regimes. Furthermore, when the degree of transparency is low, variables such as market sentiment may intervene in the decision process. Neglecting this element may explain why policies have so often suffered set-backs. Moreover, from an empirical point of view, this type of variable may well fluctuate across periods. Therefore, beyond the characteristics of a regime, the present paper calls the irrevocable nature of exchange-rate policy itself into question. In this respect, the proposal for flexible or pragmatic pegs, recently suggested by Reinhart and Reinhart (2003) and Artus (2003), represents a good alternative to corner solutions. Therefore, by showing how the lack of transparency in emerging countries may explain the vulnerability of their economies to market sentiments, the present framework also helps to understand the recurrence of crises in these countries. The role of the government is first and foremost to promote full transparency. However, since transparency is sometimes difficult to achieve, choosing an appropriate exchange rate policy in accordance with the informational infrastructure of the economy would be a valuable first step. The adhesion or the non-adhesion to programmes of systematic information dissemination such as SDDS (Special Data Dissemination Standard) of the IMF should be considered for formulating appropriate exchange-rate policies.