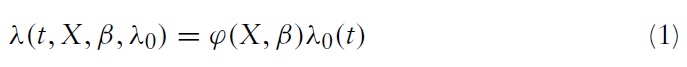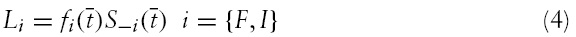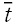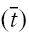Bank failures and bank mergers and acquisitions have been studied widely. However, most of the existing studies focus on two-state worlds where only two outcomes are possible.1 While research on bank failure concentrates of finding the factors that influence the transition of a surviving bank to liquidation (Lane
In this paper we use duration analysis and competing risks models to simultaneously find the significant determinants of the probabilities of failing or participating in an integration(M&A)process for financial institutions in Colombia. We use an especially rich data set comprised of monthly information on banks’ balance sheets for the period January 1997 – December 2000. During that time span Colombia experienced a severe financial crisis that led to a significant contraction and concentration of the country’s financial system.2 Our hypothesis is that during times of financial stress some institutions participate in integration processes as a strategy to survive. However, not all institutions are allowed to participate in such processes. In particular, those banks whose financial health deteriorates profoundly do not find partners to merge and are not acquired, and therefore are more likely to be liquidated than peers in better financial conditions.
The case of Colombia is worthy of study because, during the late 1990s and early 2000s, many bankruptcies and M&A processes took place in the financial sector, due to the financial crisis and to the process of consolidation of an incipient banking system. We focus our attention on the period of financial stress for two reasons. First, between 1997 and 2000 there is a sufficiently large proportion of failures and integrations to identify and measure significant effects of financial variables. And second, from the supervisor’s or regulator’s viewpoint, interest relies on identifying the variables that determine the probability of observing a bank failure after the occurrence of a negative shock that affects the financial system. When a bank is under stress, liquidation is just one of three possible outcomes, which include participation in an integration process and survival.3 However, the probability of participating in an M&A (and of failing, and of surviving) may be different during times of stress and in average times. Therefore, using a larger time-span could produce biased estimates of the probabilities of interest in this study.
An additional advantage of focusing in a period of financial crisis is that we can exclude macroeconomic covariates that control for the stage of the business cycle from the empirical analysis. We assume that the effect of the variation in the stage of the cycle (which must be lower when only a period of recession is considered than if a larger time-span were considered) is captured by its direct effect on microeconomic covariates and by the baseline hazard function, common to all the institutions under analysis. The exclusion of macroeconomic variables allows us to use a hazard duration model with time-fixed covariates. With the model we construct here we can provide answers to questions that are relevant for both financial supervisors and financial institutions, such as: after the occurrence of a negative shock, what is the probability that a bank fails (or, alternatively, participates in an M&A process) in the following months, given it has survived up to that moment? Or, what is the predicted time to failure (alternatively, participation in anM&Aprocess) for a bank of some given characteristics? A model capable of answering those questions at low cost can be very useful as an early warning model, to identify potential vulnerabilities of the financial system, and could be used by supervisors as an alternative to the costly on-site visits that they make periodically to financial institutions considered at risk.
We find that, as expected, differences in financial and prudence across institutions can explain the processes of failure and integration of banks and related financial institutions after the occurrence of a negative shock. While profitability and capitalization are the most important determinants of the probability of failing, bank’s size, efficiency and capitalization are the main determinants of the probability of integration. Changes in the level of capitalization matter for the happening of both a failure and a process of M&A. All else constant, an increase in capitalization reduces the probability of disappearing, whether due to the occurrence of bankruptcy, a merge or an acquisition. However, a marginal increase in capitalization reduces more the probability of bankruptcy than the probability of integration. Thus, conditional on having survived up to time
The rest of the paper is organized as follows. Section 2 briefly describes the episode of financial crisis in Colombia. Section 3 is a literature review section. Section 4 presents the description of the data. Section 5 presents the empirical model used to find the determinants of the processes of failure and M&A of financial institutions, as well as estimation results. Finally, Section 6 presents conclusions.
1A notable exception is Wheelock and Wilson (2000), who use US banks’ data and estimate a competing risks model to consider the joint determination of the probability of failing, being acquired, or surviving. 2As a consequence of the crisis, the number of institutions, 138 in January 1997, dropped to only 57 in December 2001, after failures, mergers and acquisitions. Total assets of the financial system experienced a real contraction of more than 20% during the same period, making that episode of financial stress the deepest financial crisis experienced by the country in the last century (Gómez-González & Kiefer, 2009). 3We consider participating in an integration process as a different outcome from survival, because in an integration process the participating institutions merge into a new institution different from those that existed before. Indeed, the decision to participate in an integration process is different from the decision to maintain the firm’s corporate structure and wait and see if the institution survives or not.
2. The Financial Crisis in Colombia in the Late Twentieth Century
Financial liberalization was a common factor among developing economies during the late twentieth century. The promised advantages of financial globalization led most emerging economies to liberalize their financial systems around the first half of the 1990s (Schmukler & Vesperoni, 2006). Colombia was not a stranger to this process of change and, at the beginning of the 1990s, a program of financial liberalization was implemented. After a long period of financial restriction,4 conditions for the entrance of foreign investment were eased, promoting more competition in the financial system, and financial institutions were given more liberty in the management of financial operations and interest rates.
The ratio of intermediated assets (loans plus bonds) to GDP increased from 31% in 1990 to 47% in 1996. The number of financial institutions increased significantly, the participation of the assets of foreign banks in the total assets of the system increased, and most of the government-owned financial institutions were privatized.
As a consequence of the growth in the financial system and of the economic expansion that took place during the first half of the 1990s, between 1991 and 1997 Colombia registered a credit boom without precedent. The ratio of loans to GDP and the price of assets (financial and real) grew steadily, as did the number of intermediaries. But, as is often the case when quick expansion of credit follows financial liberalization, the quality of loans of financial institutions decreased, and this degradation of loan quality elevated the financial fragility of the economy (Minsky, 1982).
Between 1998 and 1999 a sudden capital reversion occurred, followed by a steep fall in the terms of trade, which led to a reduction in the aggregate level of expenditure. Internal demand fell while interest rates increased to historically high levels. The housing price bubble burst, while the prices of financial assets collapsed. The financial health of financial intermediaries damaged sharply. Loan quality decreased (i.e., the rate of non-performing loans to total loans for the system increased from7.9% in June 1998 to16%by the end of 1999), and the losses of financial institutions,which had very lowlevels of provisions, led to a reduction of capital and a worsening of capitalization. Many banks were liquidated, while others merged or were absorbed by other financial institutions.
Overall, the period of financial stress generated a reduction in the size of the financial intermediation industry of Colombia and a change in the composition of the financial system’s assets. In terms of size, the ratio of intermediated assets to GDP fell to 38% in 2000. In terms of asset composition, loans rendered up participation to securities. Lending policies became stricter. For instance, the ratio of provisions to loans of surviving institutions grew steadily. Concentration increased in the financial system, mainly due to the processes of liquidation and M&A of institutions that took place during the period of stress.
Hand-by-hand with the financial crisis, Colombia experienced a deep economic recession. Between 1999 and 2003, growth slowed by 4.2% and investment by 34.6%. As shown by López andRodríguez (2008), a financial accelerator mechanism à la Bernanke
Many other emerging economies suffered periods of financial distress during the late 1990s.6 These financial crises, also observed after periods of rapid credit expansion, are well documented in the literature (for instance, Kaminsky & Reinhart, 2001; Bae
4During the 1980s, Colombia’s financial institutions had high reserve requirements imposed upon them, and investments forced on them. Strong constraints on foreign investment existed, as well as on the types of operations intermediaries could do and on interest rates. Additionally, a process of bank nationalization was held during that decade. 5This is not a surprising result, given that in Colombia firms are highly bank-dependent. Huertas et al. (2005) show that near 60% of total firms’ funding is provided by financial institutions 6Mexico, 1994–95; East Asian countries, 1997–98; Russian, 1998; and, Brazil, 1998–99.
Bank failures and bank mergers and acquisitions have been traditionally studied separately. The literature on bank failures is ample. A good review of the early literature is presented by Demirguc-Kunt (1989). Different statistical techniques have been used to predict bank failures or to discriminate between sound banks and those prone to fail, mainly using data from financial institutions in the US. Among them are the Z-score, develop by Altman (1968) in order to forecast the probability of a bank entering bankruptcy within a two-year period; multivariate discriminant analysis, used by Sinkey (1975); event analysis, followed by Lane
Regarding mergers and acquisitions, the empirical literature can be divided into two groups. The first one corresponds to studies on the causes and consequences of M&A events (efficiency gains or losses, for example). The second one consists of empirical analyses using probability models to estimate the likelihood of participating in these actions. Regarding the second group of studies, the seminal works are those of Hannan and Rhoades (1987) and Amel and Rhoades (1989). Both studies use data from banks in the US and estimate logit models to identify significant factors determining the probability of an integration process. Focarelli
There are a few papers on the determinants of integration processes that have used competing risks models to model separately the chance of participating in a process of M&A as an acquiring entity or as an acquired firm. One interesting recent example is García-Suaza and Gómez-González (2010).
In contrast with the studies on bank failure, research on the determinants of the probability of observing a merger or acquisition use data on banks for prolonged time-periods. One reason of doing so relates to the fact that many mergers and acquisitions do not correspond to a safeguard strategy followed by a bank to avoid failure, but correspond to a strategy followed by two or more institutions in order to gain market power. During tranquil times it is to be expected that most M&A processes correspond to the second type of strategy (the search of greater market power), while during times of distress it is to be expected that most of these processes correspond to the first type of strategy (Focarelli
All of the above-mentioned studies focus on two-state worlds where only two outcomes are possible. For traditional studies on bank failure, the two possible states of nature are survival and liquidation. In this case, M&A are either modeled as censured data or ignored. For studies on M&A, the only possible final outcomes are survival as an independent entity and fusion,while bank failures are either modeled as censured data or ignored. Only a limited number of papers have studied simultaneously the transition from survival to either liquidation or integration. The seminal study is Wheelock and Wilson (2000), who use competing risks hazards models to identify characteristics that make individual banks in the US more likely to fail or to be acquired. A related recent paper is Brown and Dinc (forthcoming), who study bank failures in a group of emerging market countries in the 1990s. Their interest, however, is to check whether observed differences in the strength of the banking systems across countries influences the likelihood of the Government in taking over or closing a failing bank.
There are no studies on the competing risks of failing or merging for emerging economies.This paper is thought to be the first to present a competing risks hazardmodel to simultaneously identify covariates that excerpt significant influence on the probability of failing or merging for banks of an emerging economy.This study is close in spirit to Wheelock andWilson (2000). However, unlike themwe focus in a period of financial distress, namely the financial crisis experienced by Colombia during the late 1990s.7 We benefit from an unusually rich database that offers us two advantages with respect to previous studies. First, survival is measured on a monthly scale, which helps us identify more precisely the moment of failure or integration of financial institutions.8 Second, due to Colombia’s financial crisis, there are enough failures and integrations to identify and measure significant effects of financial variables.
7Wheelock and Wilson use information for the period 1984–1993. They use a larger time-span in order to record enough failures and mergers and acquisitions to be used in their empirical work. 8Most of the previous studies use quarterly data, which is the frequency with which financial institutions report their balances to the supervisors in many countries.
This paper studies failures and M&A during the Colombian financial crisis of the late 1990s. The period of observation is the 48 months between January 1997 and December 2000. Data are observed in a monthly frequency. Financial data as of January 1997 was collected for each of the banks9 that existed at that date.10 Some studies on bank failure only include in the sample a subset of the group of banks. For example, Oshinsky and Olin (2005) study only banks in trouble, defining them as those that receive a composite CAMELS rating of either 4 or 5 when examined. However, it is not only banks that actually change state or that are more likely to change state ex-ante that provide valuable information to understand bank failures and M&A. Solid banks, or banks that have a lower chance ex-ante to change state, also provide valuable information.
Following previous studies and theoretical expectations, the following financial ratios were included as covariates: capitalization (CAP), defined as the ratio of equity to assets; management efficiency (EFF), approximated by the ratio of operating expenses to average annual assets (this variable is in fact constructed as a proxy of inefficiency); profitability of assets (PROF), given by the ratio of annualized profits to average annual assets; liquidity (LIQ) defined as the ratio of short-term liabilities to liquid assets; and, a market-based variable (SIZE), defined as the natural logarithm of the bank’s assets. These financial indicators are proxies of the variables traditionally considered in the literature.
The data set used to construct the covariates consists of information in the balance sheets that financial institutions report periodically to the Financial Superintendence of Colombia.11 Table 1 shows a summary of these variables. Information is reported for the average of surviving institutions, for the average of institutions that merged or were acquired, and for the average of failed institutions.
Note from Table 1 that institutions that survived the period of financial distress showed in January 1997 better indicators of financial health than other institutions on average. They were better capitalized, more efficient, and more profitable. It is very interesting to note that there are also notable ex-ante differences between failed banks and banks that integrated with others during the period. In particular, banks that participated in an M&A process showed better financial indicators at the beginning of the observation period than banks that finally went to bankruptcy. If only survival and bank failure were considered, information on banks that participated in an integration process during times of financial distress would at the most be used as censured data. The inclusion of the ‘intermediate’ state of the world (M&A) leads to a better understanding of the behavior of financial institutions during tough times.
[Table 1.] Summary of the financial ratios used in the empirical analysis by type of institution

Summary of the financial ratios used in the empirical analysis by type of institution
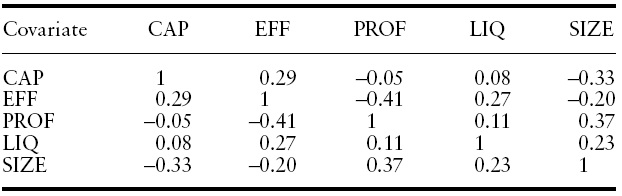
[Table 2.] Pair-wise correlation matrix
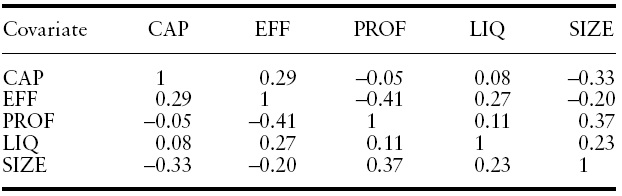
Pair-wise correlation matrix
Most pair-wise correlations between the included variables were small and in no case did one exceed 0.41 in absolute value (Table 2). We excluded from the empirical analysis variables that exhibited high pair-wise correlations with at least one of the covariates that appear in Table 1, to avoid potential problems of multicolinearity.
From Table 2 it can be see that the linear correlation between CAP and PROF is low. The Spearman correlation between both variables is also low and not statistically different from zero. The relation between current CAP and lagged PROF is also weak. Therefore, it appears to be the case that PROF is not a good predictor of CAP according to the data used in this empirical study.
Regarding failure and integrations, the empirical probability of failure before 48 months after the occurrence of a strong negative shock is 21.7% (30 out of 138 institutions failed). That percentage of failures is way above the percentage of failures in Wheelock and Wilson (2000), Carree (2003), and other related studies. However, the empirical probability of merging, acquiring, or being acquired is even higher: 34.1%. These high percentages show that the case of Colombia is a very interesting one to study. The large number of observed events allows a very fine measurement of the influence of individual variables on the probability of observing an event.
Our sample does not allow us to do separate analysis for banks depending on whether they are private or public, because in our sample only one bank is public. All the rest are private. For similar reasons, we cannot evaluate whether the probability of taking on a particular state (surviving, merging, or failing) depends on the origin of bank’s capital (national or foreign). Very few banks in the sample are foreign banks.
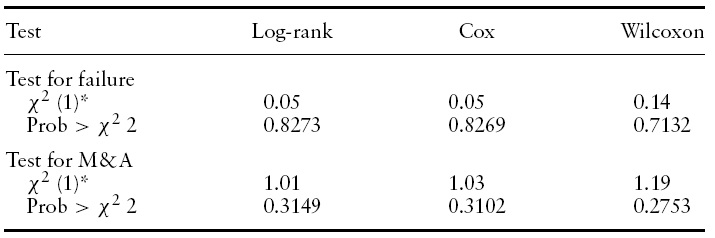
Tests for the equality of the survivor functions. Null-hypothesis: Commercial banks and financial companies have identical survival functions between January 1997 and December 2000
9Our data collects information on commercial banks and financial companies. Financial companies in Colombia are quite similar to commercial banks (they are ‘small’ banks). Indeed, as shown below, both have statistically identical survival functions for the period of study. Thus, we treat them indistinctly as banks. 10In this paper we do not report results when time-varying covariates are included given the question of interest that was presented in the introductory section. Additionally, specification tests for the assumption of proportional hazards indicate that a specification with time-fixed covariates is adequate. As a robustness check of the results reported here, we estimated an identical model with time-varying covariates. The results were fundamentally the same. 11The Financial Superintendence is the regulator of financial institutions in Colombia.
5. Empirical Model and Estimation Results
We use a hazard function model to study the time to failure or participation in an integration process of financial institutions. This approach generalizes the more common binary response approach by modeling not only the occurrence of the event but also the time it takes an individual to change state (allowing a more efficient use of the available information). Hazard function models applied to this problem can provide answers to questions that are relevant for both financial supervisors and financial institutions, such as: after the occurrence of a negative shock, what is the probability that a bank fails or participates in an integration process in the following months, given it has survived up to that moment? Or,what is the predicted time to state migration for a bank of some given characteristics?
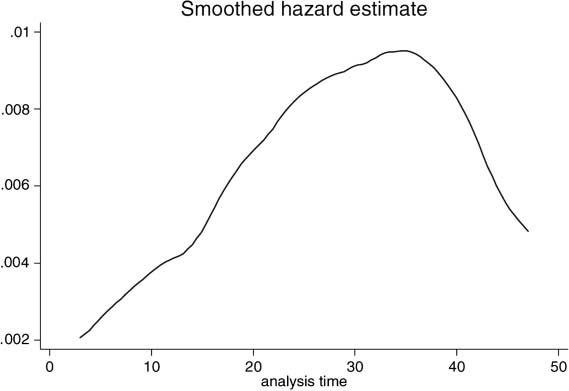
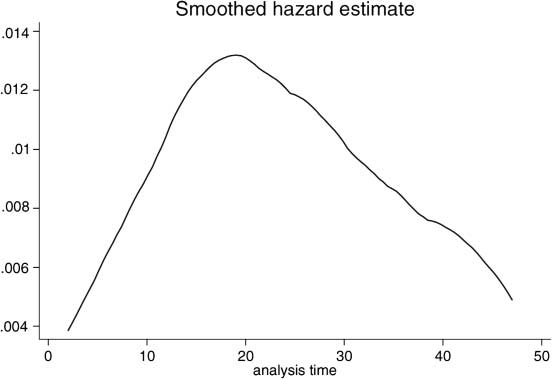
Preliminary analysis on the raw data (data not conditioned on covariates) showed that the survival functions of commercial banks and financial companies are statistically identical (Table 3). Therefore, we treat both types of institutions as one same group. Figures 1 and 2 show the hazard functions corresponding to failures and mergers and acquisitions. Both functions are clearly non-monotonic. The form of the estimated hazard functions12 shows that the most commonly used parametric models for the distribution of duration do not seem to be appropriate for modeling the baseline hazards of the migrations considered in this study. Therefore, this paper estimates a proportional hazards model in which no parametric formis assumed for the baseline hazard function, following Cox (1972). As shown below using a specification test, this assumption seems to be appropriate for the problem of interest. Nonetheless, we also report results from estimations using three parametric distributions frequently used in the literature (Exponential, Weibull, and Gompertz) to compare the proportional hazards model with other models.
Under the proportional hazards specification, the hazard rate takes the following multiplicative form (see, for example, Gómez-González & Hinojosa, 2010)
The baseline hazard function,
In this study, at every moment of time, a surviving bank faces two competing risks. It may fail and it may participate in an integration process. However, the materialization of at most one of these risks will be observed. If the bank fails, the institution arrives at an absorbent state. Thus, its chances of participating in anM&Aprocess vanish at that moment. If the bank integrates with another one, the original institution finds the end of its life while a new institution appears in the market. Thus, the original institution will no longer have a chance of failing (although the newinstitution has indeed a chance of both failing and integrating).
In order to model appropriately the two riskswe are considering,we use a competing risks model extension of the proportional hazards model presented above. Let
In equation (2),
Suppose a bank makes a transition (either fails or makes part of an integration process) at time
. Its marginal contribution to the likelihood function,
with
representing the probability density function of migrating to state
and
representing the survival function of remaining in a state different from
The total individual contribution,
In equation (6),
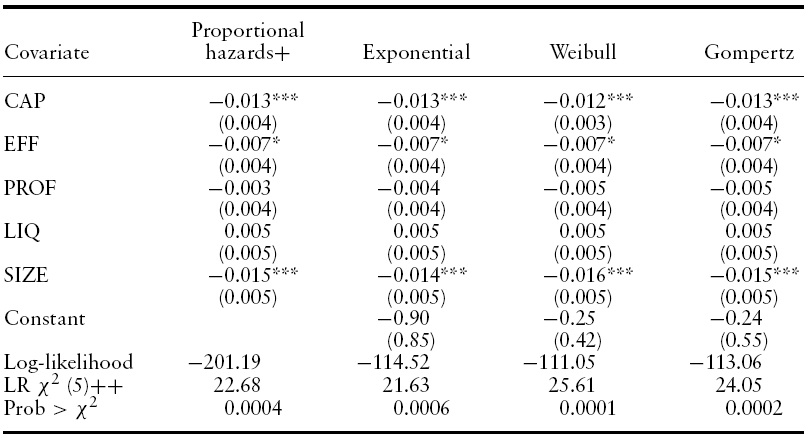
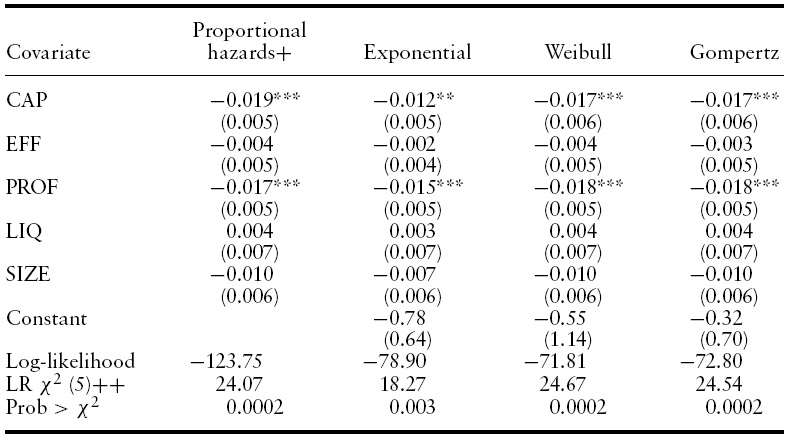
[Table 4.] Estimation results for duration to failure
Estimation results for duration to failure
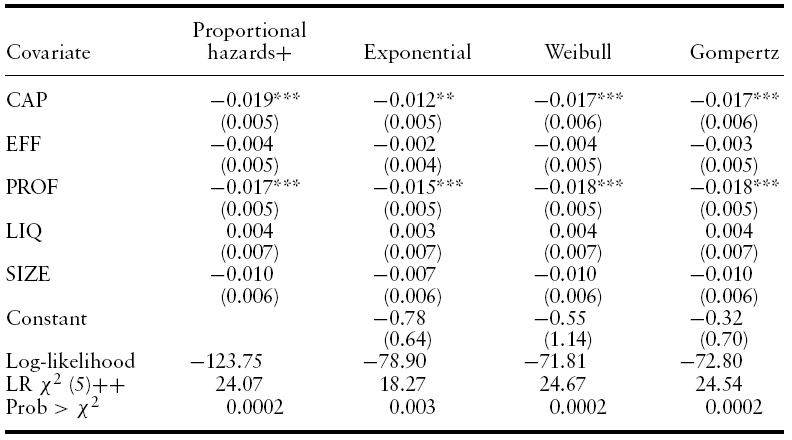
We estimated the corresponding proportional hazards competing risks model using the partial maximum likelihood method proposed by Cox (1972).14 Ties in duration are handled by applying the method of Efron (1977).15 Estimation results are shown in Table 4 (for the risk of failure) and Table 5 (for the risks of participating in an integration process).
Note from Table 4 that estimation results for the determinants of the duration to bank failure are similar under the different models. In particular, the signs of the coefficients remain unchanged as well as significance levels. In all four cases, the null hypothesis that none of the included variables significantly affects the probability of changing state is rejected at conventional significance levels. Regarding individual covariates, CAP and PROF are the most significant determinants of the duration of survival. The estimated sign for both variables is negative, indicating that an increase in one of these two variables leads to a decrease in the probability of failing, everything else constant.
Given we showed above that parametric models do not represent appropriately the behavior of the unconditional baseline hazard function we focus in the proportional hazards model’s results. According to Table 4, a 1 percentage point increase in CAP leads to a 1.9% decrease in the probability of failing. Similarly,ntage point increase in annualized assets profitability reduces the hazard rate of failure by 1.7%.
[Table 5.] Estimation results for duration to participation in an integration process
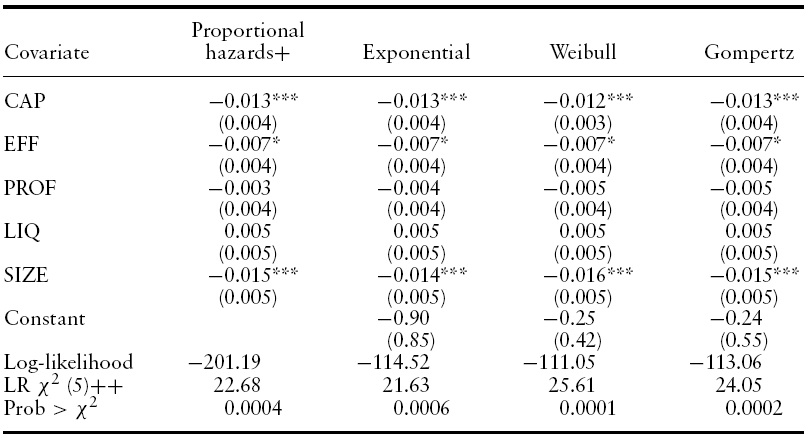
Estimation results for duration to participation in an integration process
After controlling for appropriate financial health indicators, the size of a bank does not exert significant influence on the hazard rate of failure.This is an interesting result showing that there is no evidence that during Colombia’s financial crisis a too-big-to-fail rescue policy was implemented by the financial sector regulator.
Table 5 presents estimation results for the determinants of the hazard rate of bank integration. Results are similar under the alternative estimated models. Focusing attention on the results of the proportional hazards model, CAP, EFF and SIZE are significant individual covariates affecting the transition from individual survival to participation in an M&A process. The estimated signs for the three variables are all positive, indicating that an increase in any of these three variables leads to a reduction in the migration probability under consideration. Note that EFF and SIZE, although not significant for the transition to failure, are significant determinants of the probability of participating in an M&A process. Larger banks are less likely to integrate with others. A probable explanation derives from regulation. There are laws that limit concentration in the banking industry. Therefore, there exists a threshold size over which an institution can no longer expand.
Increases in EFF (increases in inefficiency) reduce the probability of merging or being acquired. Therefore, all else constant, an inefficient institution finds it difficult to associate with others during times of financial distress. It has to try to survive alone. If, additionally, the institution is poorly capitalized or unprofitable, it will most likely fail.
Of particular interest, CAP is a statistically significant determinant of the two competing transitions studied in this paper. However, the effect of a marginal increase in CAP affects differently the probability of transition to each of the alternative states. While a one percentage point increase in CAP decreases the hazard rate of bank failure by 1.9%, it decreases the hazard rate of participating in an M&A process by just 1.3%. Recall the hazard rate represents the instantaneous conditional probability of changing of state. Therefore, a 60 basis points difference is a considerable one.
This result can be interpreted in the followingway. All else constant, after a negative shock happens an increase in capitalization reduces the probability a bank has of disappearing, whether due to the occurrence of bankruptcy, a merger, or an acquisition. However, a marginal increase in capitalization reduces the probability of bankruptcy more than the probability of integration. Thus, conditional on having survived up to time
A related alternativeway of understanding the effect of CAP is as follows. After the financial system experiences a negative shock, the shareholders of a troubled bank can choose whether or not to increase the bank’s capital. If they decide not to capitalize the bank, the chance it fails increases. On the other hand, they have the opportunity to avoid failure by capitalizing the bank. Their decision is a strategic one. They can decide to increase the institution’s capital significantly in order to guarantee it will be able to survive in its current state. Alternatively, they can decide to increase capital less, in a way sufficient enough to be able to merge with another bank, or to make the bank attractive so that others acquire it.
From the supervisor’s viewpoint, the result has an important policy implication. Using the model presented above, the supervisor can decide during times of financial difficulty which is the best policy to implement with respect to banks in distress in order to achieve financial stability. Bank by bank, they can decide whether they must intervene an institution or not and, in case an intervention is decided, which intervention is more adequate to preserve financial soundness.
With the empirical model estimated in this study it is not possible to directly find threshold values for the included covariates that separate each of the three possible states of the world. An interesting extension would be to introduce different nonlinearities on the effect of a particular covariate or group of covariates on the hazard rates and try to calculate this threshold values for different probability levels. This extension is, however, out of the scope of this study, and left for future research.
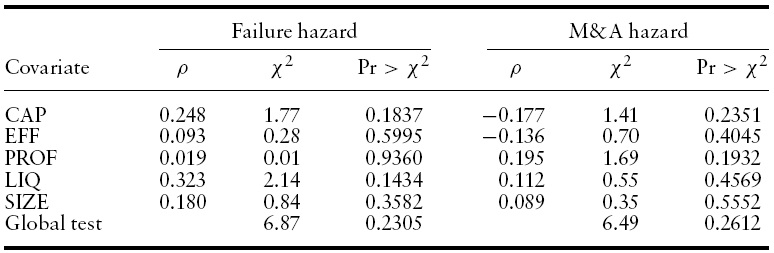
Table 6 presents evidence that the proportional hazards assumption is adequate for our sample. The proportional hazards factorization implies that the effect of the covariates on the hazard function is constant over time.This hypothesis can be tested using Schoenfeld’s residual test,which tests for a zero slope in a generalized linear regression of the residuals on time. The null hypothesis of the test is that the slope is zero. A rejection of the null hypothesis indicates that the proportional hazards assumption is unsuitable.
Table 6 shows results for a test of each covariate as well as for a global test. Note that the null hypothesis of a zero slope cannot be rejected in any case. Therefore, Schoenfeld’s residuals test provides evidence that the proportional hazards specification is adequate in this study.
[Table 6.] Schoenfeld’s residuals test results
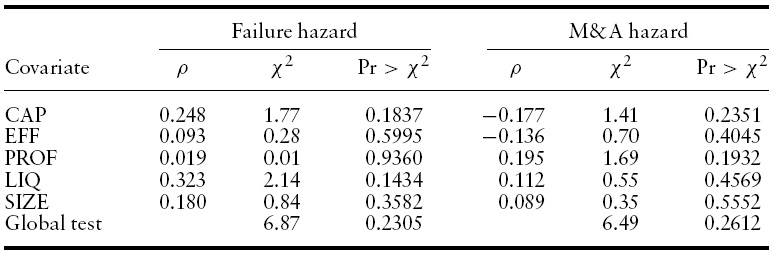
Schoenfeld’s residuals test results
12Hazard functions are estimated here as a kernel smoothed difference of the Aalen–Hansen estimator of the cumulative hazard functions.We use an asymmetric Epanechnikov kernel function. 13Independence between the competing events is conventionally assumed in the literature (Wheelock & Wilson, 2000; García-Suaza & Gómez-González, 2010). While dependent hazards can be modeled by using appropriate multivariate distributions, the data are not able to distinguish between dependent and independent models (Elandt-Johnson & Johnson, 1980). With the information available in this study it is impossible to test the null hypothesis of independence of the hazard functions, and it is also impossible to determine appropriately the structure of the possible dependence (see Lancaster, 1990). 14The parametric models, estimated for comparison purposes, are estimated by maximum likelihood. 15Hertz-Picciotto and Rockhill (1997) show that the Efron method for handling ties is to be the preferred, especially when the sample size is small either due to heavy censoring or from the outset.
This paper studies the processes of failure and M&A of financial institutions in Colombia during the financial crisis of the late 1990s. We use an especially rich data set comprising monthly information on banks’ balance sheets for the period January 1997 – December 2000. Our hypothesis is that during times of financial distress some institutions participate in integration processes as a strategy to survive. However, not all institutions are allowed to participate in such processes. In particular, those banks whose financial health deteriorates profoundly do not find partners to merge and are not acquired, and therefore are more likely to be liquidated than peers in better financial conditions.
The case of Colombia is worthy of studying because, during the late 1990s and early 2000s, many bankruptcies andM&A processes took place in the financial sector, due to the financial crisis and to the process of consolidation of an incipient banking system.We use a competing risks hazard duration model with time-fixed covariates, which allows us to answer relevant questions such as: after the occurrence of a negative shock, what is the probability that a bank fails (or, alternatively, participates in an M&A process) in the following months, given it has survived up to that moment? Or,what is the predicted time to failure (alternatively, participation in anM&Aprocess) for a bank of some given haracteristics? A model capable of answering those questions at low cost can be very useful as an early warning model, to identify potential vulnerabilities of the financial system, and could be used by supervisors as an alternative to the costly on-site visits that they make periodically to financial institutions considered at risk. Additionally, using the model, supervisors can decide during times of financial distress which is the best policy to implement with respect to troubled banks in order to achieve financial stability.
The vast majority of studies in the literature on the behavior of banks during periods of financial distress focus on two-state worlds where only two outcomes are possible. For traditional studies on bank failure, the two possible states of nature are survival and liquidation. For studies on M&A, the only possible final outcomes are survival as an independent entity and fusion. Only a limited number of papers have studied simultaneously the transition from survival to either liquidation or fusion at the same time. However, during times of difficulties, bankruptcy and integration are risks faced simultaneously by financial institutions.
This paper is the first to present a competing risks hazard model to identify covariates that exert significant influence on the probability of failing or merging for banks of an emerging economy. Specification tests show that the proportional hazard specification is appropriate for our sample. This study is close in spirit to Wheelock and Wilson (2000). However, unlike them we focus in a period of financial distress.
We find that differences in financial health and prudence across institutions can explain the processes of failure and integration of banks and related financial institutions after the occurrence of a negative shock. While profitability and capitalization are the most important determinants of the probability of failing, bank’s size, efficiency and capitalization are the main determinants of the probability of integration. Changes in the level of capitalization matter for the happening of both a failure and a process of M&A.All else constant, an increase in capitalization reduces the probability of disappearing, whether due to the occurrence of bankruptcy, a merge or an acquisition. However, a marginal increase in capitalization reduces more the probability of bankruptcy than the probability of integration. Thus, conditional on having survived up to time t, an increase in capitalization is a good signal that the bank can be able to overcome the negative shock. If the observed increment in capitalization is sufficiently large, the institution will survive and remain unchanged. However, it is also possible that the observed increment in capitalization may not be sufficient for the bank to survive by its own, but rather the bank will be forced to take part in an M&A process in order not to go bankrupt.
Our model can become an important tool for bank supervisors in emerging countries. It can serve as an early warning tool and, at the same time, can help supervisors decide which policies are best to implement in order to promote financial stability.