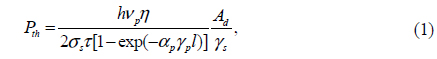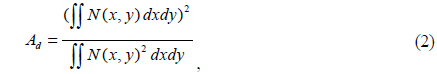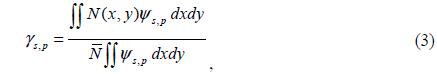Cylindrical vector beams (CVBs) have recently been receiving a considerable amount of research attention because of their unique and interesting capability of carrying orbital angular momentum [1]. In particular, CVBs can offer highly focused beam spots as well as dipole-like oscillating field patterns [2-6], which can open up opportunities for novel applications, such as optical trapping [2], microscopy [3, 4], plasmonic focusing [5], high-precision laser machining [6], etc.
To date there have been a variety of studies on generating CVBs mostly in free space, utilizing special optical components [7-11], such as prisms, crystals, polarizers, lenses, axicons, retarders, etc., or using a beam-combining technique [12]. Other studies are related with the CVB generation utilizing novel types of passive optical fibers, which include a coupling scheme to launch CVBs into a fiber by placing a polarizer directly inside the fiber [13], a formation of CVBs through a passive solid-core fiber having a modified core-index profile [14], a photonic crystal fiber with a gold nanowire [15], etc. Recently, it has been demonstrated that CVBs can also be generated directly from an active fiber, i.e. a fiber laser [16-18]. In this case, CVBs are formed via fiber cylindrical vector modes (CVMs), e.g., TE01, TM01, and HE21 modes, which are capable of maintaining their orbital angular momenta while propagating in the fiber. For example, a radially polarized beam was generated via an ytterbium (Yb)-doped fiber (YDF) laser assisted by a converging axicon [17]. Since optical fibers offer great flexibility and compactness over the bulk-optic counterparts, the generation of CVBs in an all-fiber format would be of great advantage. However, the fiber laser systems for generating CVBs that have been demonstrated so far [16-18] have limitations in terms of efficiency and practicality such that the laser efficiencies were significantly lower than that of the conventional YDF-based lasers, which can be over 80 % [19], and the systems still encompassed a number of free-space optical components other than the fiber itself (e.g., free space coupling optics, long-pass filters, mirrors, polarizers, etc.) in order for the laser to operate in a CVM. It is worth noting that such limitations are due to the fact that they utilized gain fibers having a step-index core profile [16-18]. In fact, the use of a step-index core fiber (SICF) as a gain medium inevitably gives rise to a severe reduction of laser efficiency because the overlap factor (OVF) between the CVM and the doped region tends to be poor compared to the case with the fundamental mode (HE11 mode) that is a non-CVM. In other words, the CVM of a SICF generally yields a ring-shaped field pattern, so that the CVM can only extract a limited fraction of energy mainly from the edge of the core. Consequently, the population inversion built up in the central part of the core does not contribute to the CVM lasing, thereby being wasted through amplified spontaneous emission (ASE) processes, which eventually gives rise to the significant reduction of the laser efficiency, as was observed in Refs. [16-18].
Here, we propose a novel ring-doped-core fiber (RDCF) design in order to facilitate the generation of a CVM in an all-fiber format [20, 21]. Optimizing the overlap between the doped area and the desired fiber mode, we find that the overlap factor (OVF) of the lowest-order CVM (LCVM) with the doped ions can exceed that of the fundamental mode, thereby leading to lower lasing thresholds for the LCVM than that for the fundamental mode. In particular, the use of the RDCF significantly reduces the unwanted loss incurred by the ASE, due to the fact that it offers much enhanced mode overlap between the active ions and the LCVM field. Therefore, one can expect that it will lead to significant increase in the overall laser efficiency.
In general, the lasing threshold
where
where
where
As a result, the OVF becomes the ratio of the optical power confined in the doped region against the total optical power guided by the fiber.
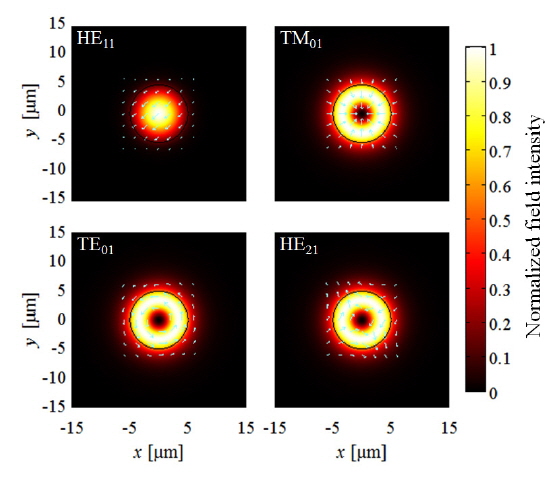
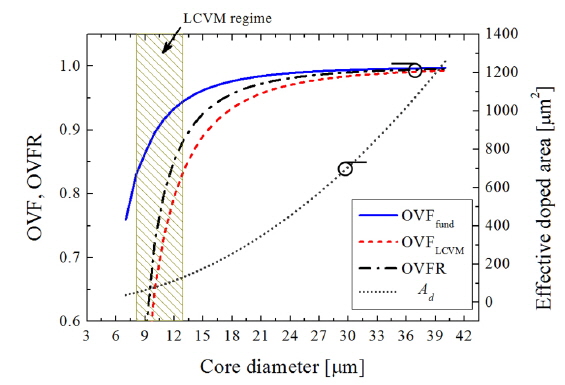
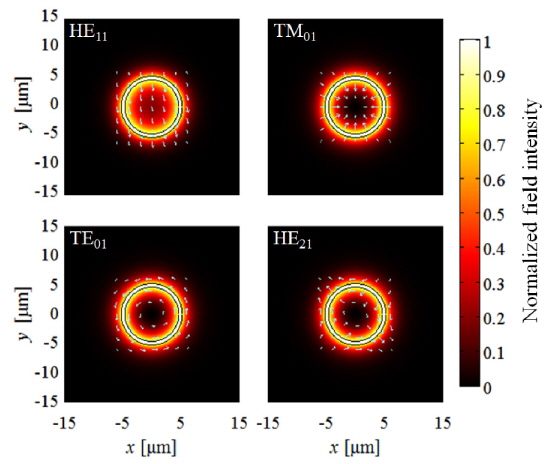
For standard SICFs, the fundamental mode and the LCVM have clearly different field patterns: The former has a Gaussian-like field distribution whereas the latter has a ring-shaped one having a zero at the center as shown in Fig. 1, where the field intensity distributions of the fundamental mode and the LCVMs (TE01, TM01, and HE21 modes) of a typical SICF having a core diameter of 9.9 μm and a core numerical aperture (NA) of 0.1.
Thus, one can expect that if a fiber is given in an SICF form and its core is uniformly doped with active ions, the
To overcome such drawbacks of SICFs in generating a CVM, we propose to use an RDCF, introducing a dopant-depleted region at the center of its core. The central dopant-depleted region will prevent the unwanted ASE build-up, and also lead to a good mode overlap between the doped ions and the CVM field.
3.1. Limitations of a Step-index Core Fiber (SICF)
Regarding the fibers under consideration, we utilize a finite-element-method (FEM)-based mode solver (COMSOL Multiphysics®) to obtain the rigorous two-dimensional mode-field distribution. We set the lasing wavelength of interest to be 1.06 μm, assuming that the fiber is doped with Yb ions. In addition, we fix the core NA to be 0.1, which is a typical value for conventional YDFs having an intermediate mode size [24, 25].
Based on these fiber parameters, we first calculate the OVFs of the SICF modes, varying the core diameter. Then, we calculate the overlap factor ratio (OVFR) of the LCVM with respect to the OVF of the fundamental mode, i.e., γs,LCVM / γs,fund. In fact, this parameter can be an indicative that shows how efficiently the fiber is capable of generating the LCVM. For example, the higher the OVFR is, the higher efficiency the fiber will have in generating the LCVM. In particular, if the OVFR exceeds unity, the lasing threshold of the LCVM will be lower than that of the fundamental mode. In addition, it is worth noting that the LCVMs include TE01, TM01, and HE21 modes, depending of their polarization states, which are all degenerate modes and have nearly identical field intensity patterns under the weakly guiding condition, as shown in Fig. 1. Therefore in terms of the OVF there are no intrinsic differences among them, and one may represent their OVF properties with one representative value hereinafter.
Figure 2 shows the calculated results for the OVFs of the fundamental mode and the LCVM, the corresponding OVFR between them, and the effective doped area
3.2. Design of a Ring-doped-core Fiber (RDCF)
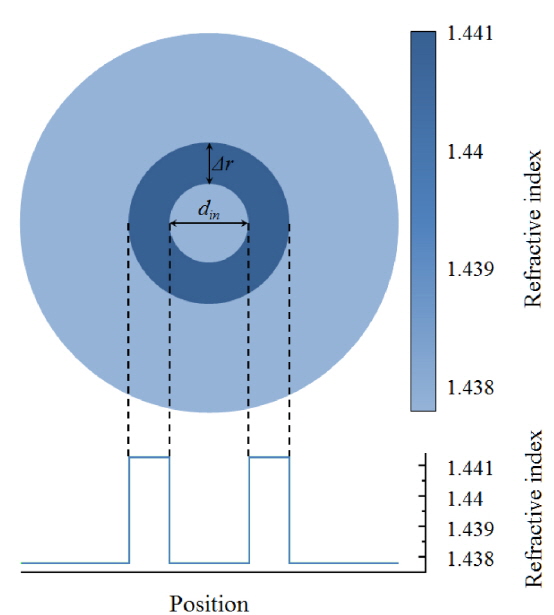
We now consider an active optical fiber having a core doped with laser-active ions, the refractive-index profile of which has an index well at the center, as depicted in Fig. 3, which is called an RDCF. We propose this structure because it can readily be implemented to a fiber via a modified chemical vapor deposition (MCVD) process [27, 28].
We assume the NA of the RDCF to be 0.1 as the same of the SICF investigated in the previous section. In fact, this NA will allow the RDCF to guide only the LCVM together with the fundamental mode if the effective mode area is scaled as similarly large as conventional YDFs having an intermediate mode size [24, 25].
We characterize the OVFs of the fundamental mode and the LCVM, varying
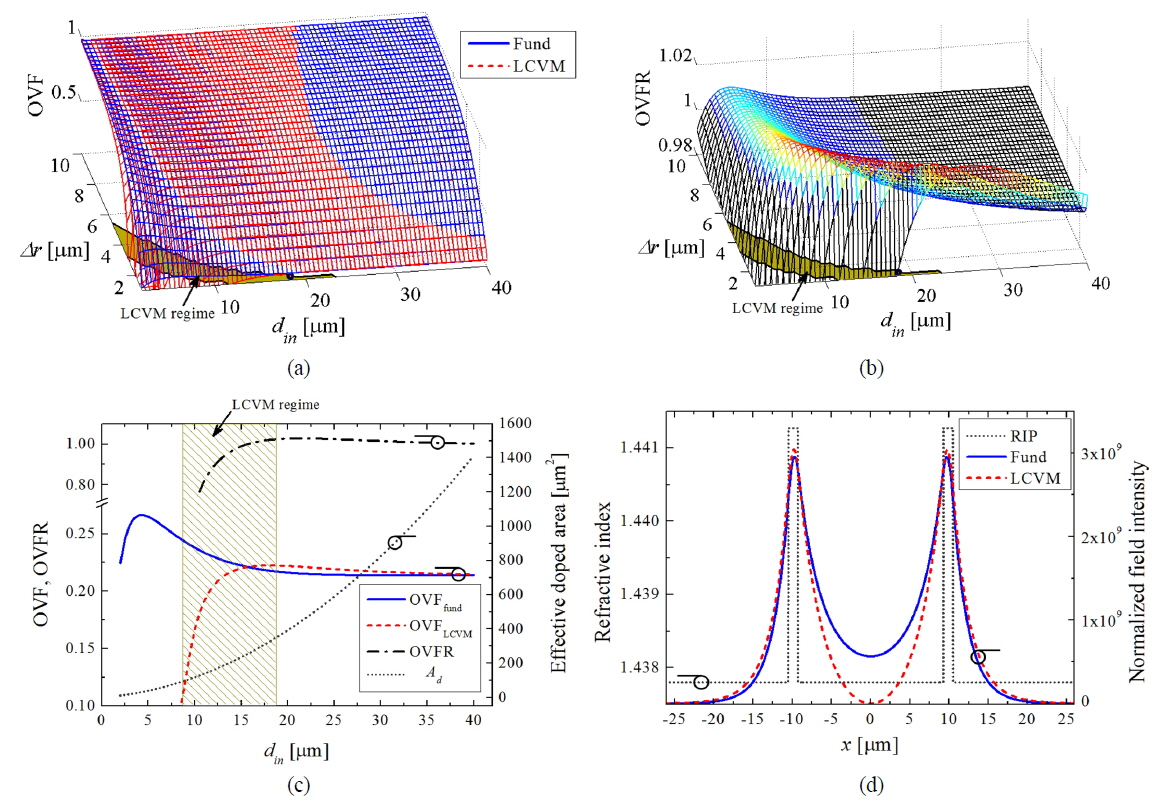
Figure 5(a) presents the OVFs of the fundamental mode (blue) and LCVM (red), and Fig. 5(b) presents the corresponding OVFR. In Fig. 5(a), one can see that a specific region exists where the red lines cover up the blue lines. This region represents the range where the OVF of the LCVM is higher than that of the fundamental mode. In particular, this range is highlighted by the color-graded lines in Fig. 5(b), which actually represents the range where the OVFR exceeds unity. The shaded regions on the bottoms of Fig. 5(a) and 5(b) represent the parameter range allowing for operating in the LCVM regime. Figure 5(c) shows the calculated results for the OVFs of the fundamental mode and the LCVM, the corresponding OVFR, and the effective doped area
Figure 5(d) shows the field-intensity distributions of the fundamental mode and the LCVM across the diameter of an RDCF having its parameter set given by
In addition, we would like to discuss a bit further the OVFR property of the optimized RDCF shown in Fig. 5(d), in comparison with various counterpart SICFs that are conventionally available. This comparison can be indicative of how efficiently the RDCF is capable of generating the LCVM. For various fiber parameter sets, Table 1 summarizes their comparative characteristics, including the NA, the core diameter, the deviation of the OVFR from unity, i.e.,
[TABLE 1.] The characteristic parameters of the optimized RDCF and various SICFs
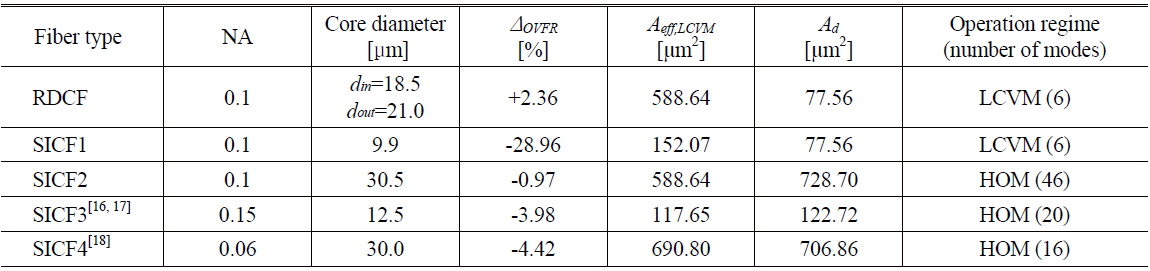
The characteristic parameters of the optimized RDCF and various SICFs
We have proposed and designed a novel RDCF that can efficiently support the LCVM generation in an all-fiber format. Through rigorous numerical analyses of RDCFs, we found that unlike SICFs, RDCFs can make the OVF of the LCVM exceed that of the fundamental mode. For an optimized RDCF that has the effective mode area of the LCVM (