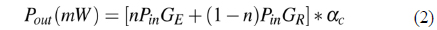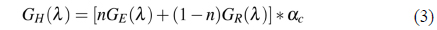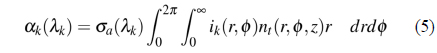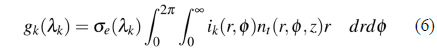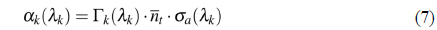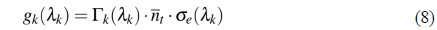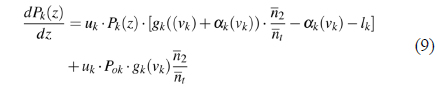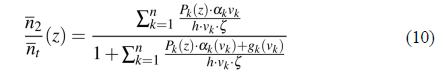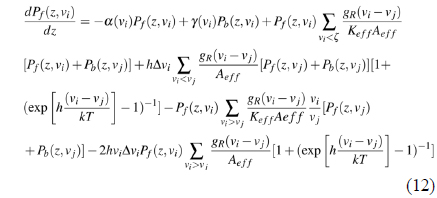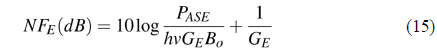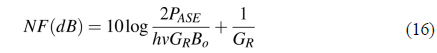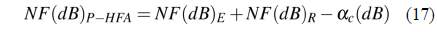Hybrid Raman/erbium-doped fiber amplifiers are an enabling and promising technology for future dense wavelength-divisionmultiplexing (DWDM) multi-terabit systems, as it has been shown by recent experimental results [1-7]. Hybrid fiber amplifiers are designed to maximize the span length, minimize the impairments caused by fiber nonlinearities, enhance erbium doped fiber amplifier (EDFA) bandwidth, provide sufficient increase in overall signal gain and enhance the pump conversion efficiency [8-11]. Two main configurations were used in the design of the hybrid fiber amplifiers; serial hybrid fiber amplifiers (S-HFA) and parallel hybrid fiber amplifiers (P-HFA).

In serial architecture, the input signal has two stages of amplification based on a single path, In other words, the output signal of the first stage is used as an input signal for the second stage. Even though this type of amplifier has high overall gain and an acceptable noise figure, there is still an issue in gain flatness. Masuda et. al. in 1998 reported a wide 3-dB gain-bandwidth hybrid fiber amplifier without using any gain-equalizer to produce a flat gain spectrum for a 76 nm range from 1531.5 nm to 1607.5 nm. However, the design used three amplification stages and five laser diodes as pumping sources, one unit to pump the EDFA and four units with different operating wavelengths to pump the Raman fiber amplifier (RFA) [12].

In 2008, Liang et. al. reported an S-HFA with wide (65 nm) amplification bandwidth from 1530 nm to 1595 nm and lower gain variation (< 0.2 dB) [13]. However, to get the low gain variation, a complicated array of fiber Bragg grating mirrors was employed.

The P-HFA in which the input signal was separated into two wavelength bands (C and L) was reported in [14-16]. One method used to improve gain flatness is to split pump power going into gain media. The optimum ratio of pump power going to erbium and Raman was found to be 1:29. The reported gain is 3-dB at input signal power of -20 dBm. However, as the input power increases, the gain variation degraded to 4 and 6dB at input signal power of -10dBm and 0dBm, respectively.

In this paper, we proposed a new P-HFA concept where, instead of dividing the pump power, the input signal is divided into two. The gain spectrum flatness is controlled by varying the input signal ratio. Wide flat gain bandwidth over a range of 60 nm from 1530 nm to 1590 nm was obtained at input signal power range from -30 dBm to -5 dBm.

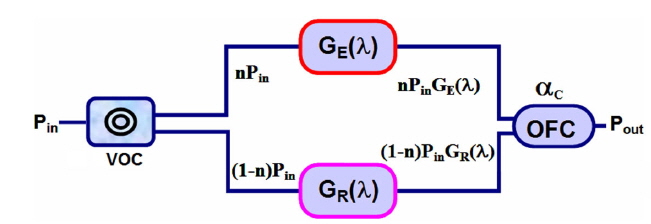
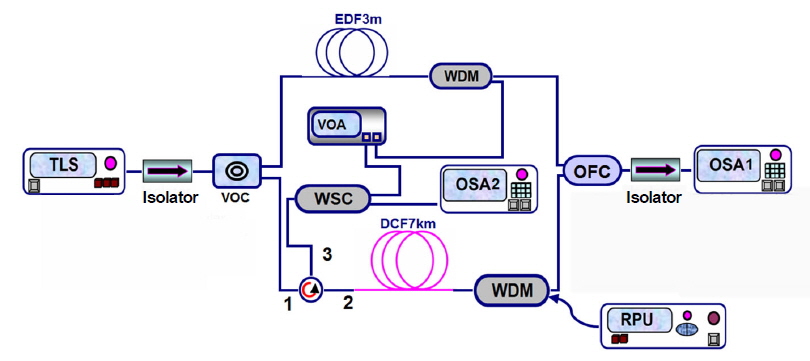
Figure 1 shows the power tracing of the light path for the proposed P-HFA. The VOC is used to control the input signal power ratio. In this equivalent light path diagram, the power tracing is adopted to calculate the overall hybrid gain.

The hybrid gain GH is given by:

where, 0 < n < 1 represents the coupling ratio of VOC, P_in (mW) is the input signal power, P_out (mW) is the output signal power, G_E and G_R are the gain factor of the EDFA and RFA, respectively and α_C is the OFC loss factor.

Thus, the P-HFA gain factor as a function of signal wavelength λ is:

G_E in Eq.(3) is based on a derived model presented by [17]. Three fiber parameters were used in this proposed model which are: absorption coefficient (α_k), gain coefficient (g_k), and a fiber saturation parameter (ζ). These parameters are obtained by conventional fiber measurement techniques covered by [17]. The saturation parameter can be defined theoretically as:

where: b_eff is the equivalent radius of the doped region, n_t is the local erbium ion density and τ is the metastable lifetime parameter.

The absorption and gain coefficients are expressed in terms of distributions of the ions and optical modes:

where, σ_a(λ_k) and σ_e(λ_k) are the absorption and emission cross-section of the k^th beam and i_k(r, ϕ) is the normalized optical intensity.

For a uniform ion distribution, the absorption and gain coefficients can be simplified as:

where: Γ_k (λ_k) is the overlap integral.

The propagation equation in terms of saturation parameter, and absorption and emission coefficients in [17]:

where each beam propagates in the forward u_k=1 or backward u_k=-1 direction, and the spontaneous emission contribution from the local metastable population and l_k is the background loss. The steady-state solution of the rate equation can be rewritten as:

Finally G_E is presented as the ratio of the output signal power to the input signal power [18]:

where: P(0) represent the input signal power and P(L) is the output signal power obtained by solving Eq.(10) under the homogeneous line broadening case.

In addition, G_R in Eq. (3) is obtained by solving the output signal power equation using the numerical solution presented by [19]:

where v_i and v_j are frequencies, g_R is the Raman gain coefficient, α(v) is the fiber attenuation, γ(v) is the Rayleigh backscattering coefficient, g_R(v_i-v_j) is the Raman gain coefficient for frequency difference (v_i-v_j), P_b(z, v_i) is the backward propagating power including sampled, parameterized, and noise bins signals, A_eff is the effective core area, K_eff is the polarization factor, Δ𝜐 is the frequency interval, h is Plank’s constant, k is the Boltzmann’s constant and T is the absolute temperature.

Raman gain reference pump and the Raman peak gain are needed in the simulation. Therefore, these two values were obtained by solving the following formula derived by [19].

where, P_R is the Raman gain peak, λ_P is the gain reference pump and g_N is the normalized Raman gain. Finally, G_R was calculated as the ratio of the output signal power to the input signal power [20]:

where P(0) is the input signal power and P(L) represents the output signal power obtained form Eq.(12).

In terms of the NF of P-HFA, the EDFA NF was presented by [18], given as:

where P_ASE is the generated noise in EDFA, h is Planck’s constant, v is the optical frequency of the input signal in Hz, G_E is the gain of the EDFA and B_o is the optical bandwidth in Hz.

The NF in RFA can be simply estimated by calculating the Raman gain G_R and the P_ASE power [21]:

where P_ASE and G_R represent the generated noise and the gain in the RFA respectively.

The summation of Eqns. (15) and (16) can represent the hybrid gain because the signal is split into two identical source (in term of λ) to be amplified by different gain media.

In the simulation design the bi-directional fiber model is adopted as a Raman gain medium. In this model, pump-to-pump, signal-to-signal and pump-to-signal Raman interactions, spontaneous Raman emission and its temperature dependency and stimulated Raman scattering (SRS) are considered. In addition, the pump depletions due to Raman energy transfer, high-order Stokes generation, multiple Rayleigh backscattering, fiber loss and spontaneous emission noise were also considered. Moreover, the stimulated Brillouin scattering (SBS) and pump depletions due to SRS effects are included in this model [22, 23].

Figure 2 shows the design of P-HFA. A variable optical coupler is used to control the input signal power between the two branches (EDFA and RFA). The input signal is provided by a tunable laser source (TLS) with power range from -30 to -5 dBm at wavelength range from 1530 nm to 1595 nm with linewidth of 150 kHz. The RFA is a 7 km of dispersion compensating fiber (DCF), pumped in a counter pump direction by a Raman pump unit (RPU) with output power of 800 mW at 1480 nm. The DCF has total loss of 4.4 dB, effective area of 18.5 μm², nonlinear coefficient of 14.5 × 10^-10 W^-1 and dispersion parameter of -110 ps/nm/km. The EDFA is a 3 m erbium doped fiber (EDF) pumped by the residual Raman pump power about 75 mW, controlled by a variable optical attenuator (VOA). The Er³⁺ ion concentration is 440 ppm, core radius is 1.9 μm, Er doping radius is 1.9 μm, and cut-off wavelength is 1300 nm. A wavelength selective coupler (WSC) is used to separate the residual Raman pump from the reflected Rayleigh scattering signal. An optical fiber coupler (OFC) is used to collect the output signal from the two branches. Finally, two optical spectrum analyzers are used, the OSA1 to record the total system gain and OSA2 to record the Brillouin Stokes power.

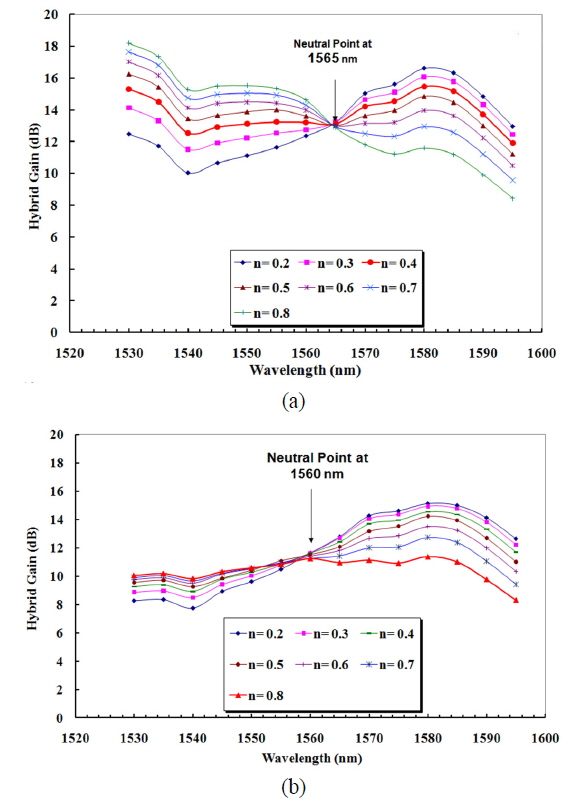
The overall gain profile of different coupling ratios with P_in of -30 dBm and -5 dBm is depicted in Fig. 3 (a) and (b), respectively. The hybrid gain values are calculated using Eq. (4). The coupling ratio n represents the percentage of input signal power that goes into EDFA.

The overall gain spectra can be divided into three regions: 1) C-band region where EDFA is more effective, 2) L-band region in which the RFA is more efficient and 3) neutral region or balance point where the input signal is amplified by equal gain from both EDFA and RFA for all coupling ratios.

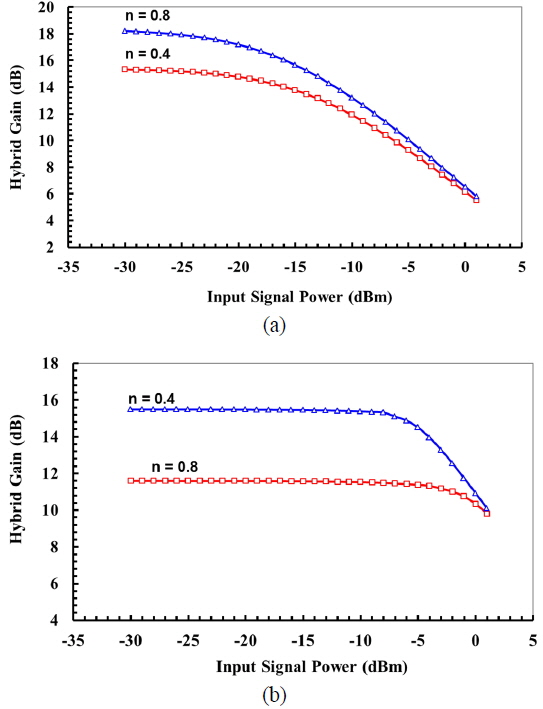
For small P_in (-30 dBm), as the n value changes from 0.2 to 0.8, the gain shows decreasing trend from 1525 nm to neutral point (1565 nm) and increasing trend from there on until 1595 nm. At n = 0.4, the gain variation is smallest compared to others. For large input (-5 dBm), as depicted in Fig. 3(b), the trend is similar but the neutral point is slightly shifted to 1560 nm. The best gain variation is when n = 0.8.

At small input signal, no saturation occurs in RFA for both n values while the EDFA starts to saturate at signal power above -15 dBm causing the hybrid gain to decrease (Refer Fig. 4). As a result to this saturation effect in the EDFA, an increment in n factor is required to increase the C-band gain level and produce wide gain flatness.

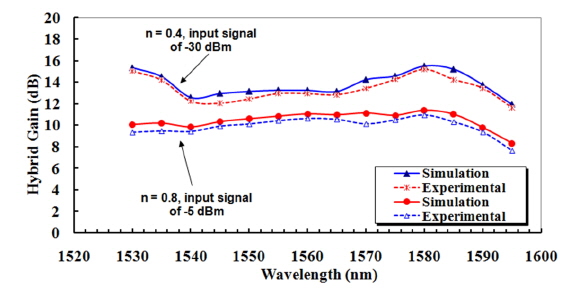
The simulation was validated by experiment for two values of n, 0.4 and 0.8 since they give the best gain flatness for small and large signal, respectively. The hybrid gain spectra are illustrated in Fig. 5. The experimental result shows very close agreement with the simulation where the gain average obtained experimentally is 13.3 dB for small signal and 9.9 dB for large signal. The gain variation is 1.06 dB at small signal and 0.77 dB at large signal for simulation while the values obtained from experiment are 1.07 and 0.81 dB, respectively.

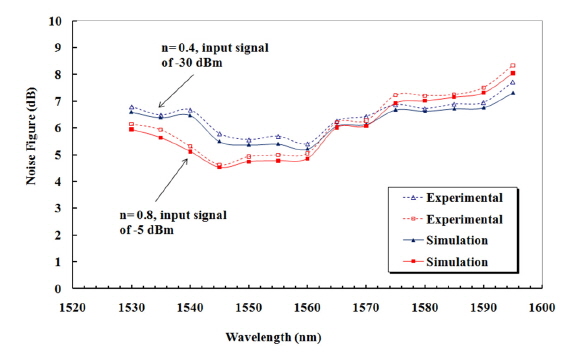
The simulated and experimental noise figure (NF) is shown in Fig. 6. The highest NF value of the small and large input signals in the C-band region was recorded at 1530 nm. This is because of the noisy amplifier spontaneous emission (ASE) at the short wavelength range. The worst NF in the L-band was observed at 1595 nm caused by steep gain drops, as it is quite far away (15 nm) from the maximum Raman gain at 1580 nm.

The gain performance of a new gain-controlled P-HFA design is simulated and experimentally demonstrated. A wide gain bandwidth of 60 nm from 1530 nm to 1590 nm is obtained with input signal less than -5 dB. The gain variation is about 1.06 dB at small input signal. This variation is enhanced and reduced to 0.77 dB at the large input signal. The gain flatness is improved and the gain dynamic range is increased as well compared with the conventional P-HFA. Finally, the experimental results show good agreement with the simulation result.