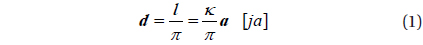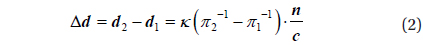In the 15^th century of the Joseon Dynasty, during the reign of King Sejong(1418-1450), various astronomical instruments were developed. In Sejong sillok (世宗實錄, the veritable record of King Sejong), there is a summary of astronomical instruments made from the period of July 1432 (the 14^th year of Sejong) to January 1438 (the 20^th year of Sejong) by the scholars of Jiphyeon-jeon (Hall of Worthies) and the astronomical officials of Gwansang-gam (Royal Observatory). Lee Cheon(李蕆), the Ganuidae jejo (簡儀 臺提調) took a leading role in making those astronomical instruments in the Ganuidae Project, which lasted for about 5.5 years (Nha et al. 1992, Jeon 2011). Those instruments comprised Ganui(簡儀, a simplified armillary sphere), Dae gyupyo(大圭表, a large measuring-scale and gnomon), the water-powered Honcheonui (渾天儀, an armillary sphere, in other words, Honui) and Honsang (渾象, a celestial globe), Angbu ilgu (仰釜日晷, a scaphe sundial), Ilseong jeongsiui (日 星定時儀, a sun-and-stars time-determining instrument), So ganui (小簡儀, a small, simplified armillary sphere), and Hyeonju ilgu (懸珠日晷, a plummet sundial). Most of these astromical instruments also had markings of angle, time, and direction on their spheres, circles, and rings.

There have been several attempts to make replicas of the astronomical instruments from the Joseon Dynasty (Nam 1989, Nha et al. 1992, Lee 1996, Kim 1997, Lee et al. 2006, Lee & Kim 2011, Lee at al. 2011, Lee & Kim 2012). However, the markings on the spheres or circles of these replicas were engraved using modern technology and knowledge. In this paper, some specifications of early Joseonese astronomical instruments are summarized. A scale marking method regarding the circumference of spheres or circles was examined using a stone-carved astronomical chart, Honsang, and Hyeonju ilgu.

Astronomical instruments made in the early Joseon Dynasty are categorized into two types: restored astronomical instruments and creative astronomical instruments. The restored astronomical instruments were quite large usually and built based on the astronomical literatures of old Chinese dynasties. In contrast, the creative astronomical ones, which were relatively small in scale, were made using technical know-how acquired during the process of building the restored astronomical instruments.

Typical restored astronomical instruments are Honsang, Honui, and Dae gyupyo. In Sejong sillok, there is no description on the detailed structures or specifications of those instruments. Instead, there are only descriptions of the Chinese literatures referenced and the places where the instruments were installed. Meanwhile, although there is currently a debate on the replica of the original Cheonsang Yeolcha Bunyaji do (Rufus 1913, Koo 2007, Ahn 2010, Ahn 2011), Cheonsang Yeolcha Bunyajido can be classified as one of the restored astronomical instruments because it was made in January 1396 during the early Joseon Dynasty. However, for So ganui, Ilseong jeongsiui, and Hyeonju ilgu, the detailed description of the shapes and dimensions is given in Sejong sillok. These astronomical instruments are not mentioned in the Chinese articles from those days and were down-sized while being built. Thus, it is speculated that these are creative astronomical instruments.

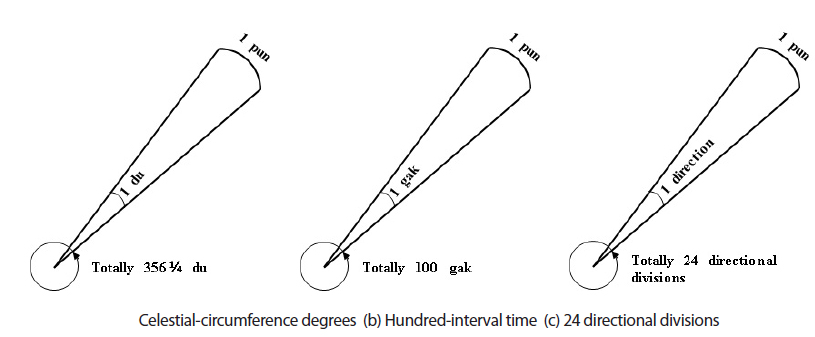
In the Joseon Dynasty, the celestial-circumference degree, also known as the great circle of celestial sphere, was divided into 365.25 dus while the time scale of a day was divided into 100 gaks (a time interval where 1 gak corresponds to 14.4 minutes today) prior to the introduction of the Shixian calendar. Also, the 24 direction systems were used. However, after the introduction of the Shixian calendar, the metrics of degree and time were changed to 360˚ and 96 quarter-of-an-hour(so called 96 gaks), respectively. Moreover, regardless of the calendar system, the twenty-eight lunar lodge system of irregular intervals and the twelve double-hour system of uniform scale were traditionally kept for the celestial-circumference degree and time, respectively. These systems were marked on the astronomical instruments of those days.

For example, in Cheonsang Yeolcha Bunyajido, there is a circular star chart with a diameter of 761 mm (Park 1998). The diameter of the circle can be divided into a coordinate circle and an outermost circle . While the degree of celestial-circumference is inscribed on the coordinate circle, twelve zodiac and 12 directions are inscribed on the outermost circle. According to the replica of the Cheonsang Yeolcha Bunyajido housed in Korea Astronomy and Space Science Institute (KASI), the longitudinal diameters of the coordinate circle and outermost circle are about 723 mm and 760 mm, respectively (Table 3). Whereas the circular star chart of the Cheonsang Yeolcha Bunyajido shows old Chinese constellations on a 2-dimensional plane, Honsang shows them on a 3-dimensional spherical surface. Also, Sejong sillok describes the circumference of Honsang to be 10.86 ja, while there is an assertion that it is a typographical error of 10.96 ja (Han et al. 2001).

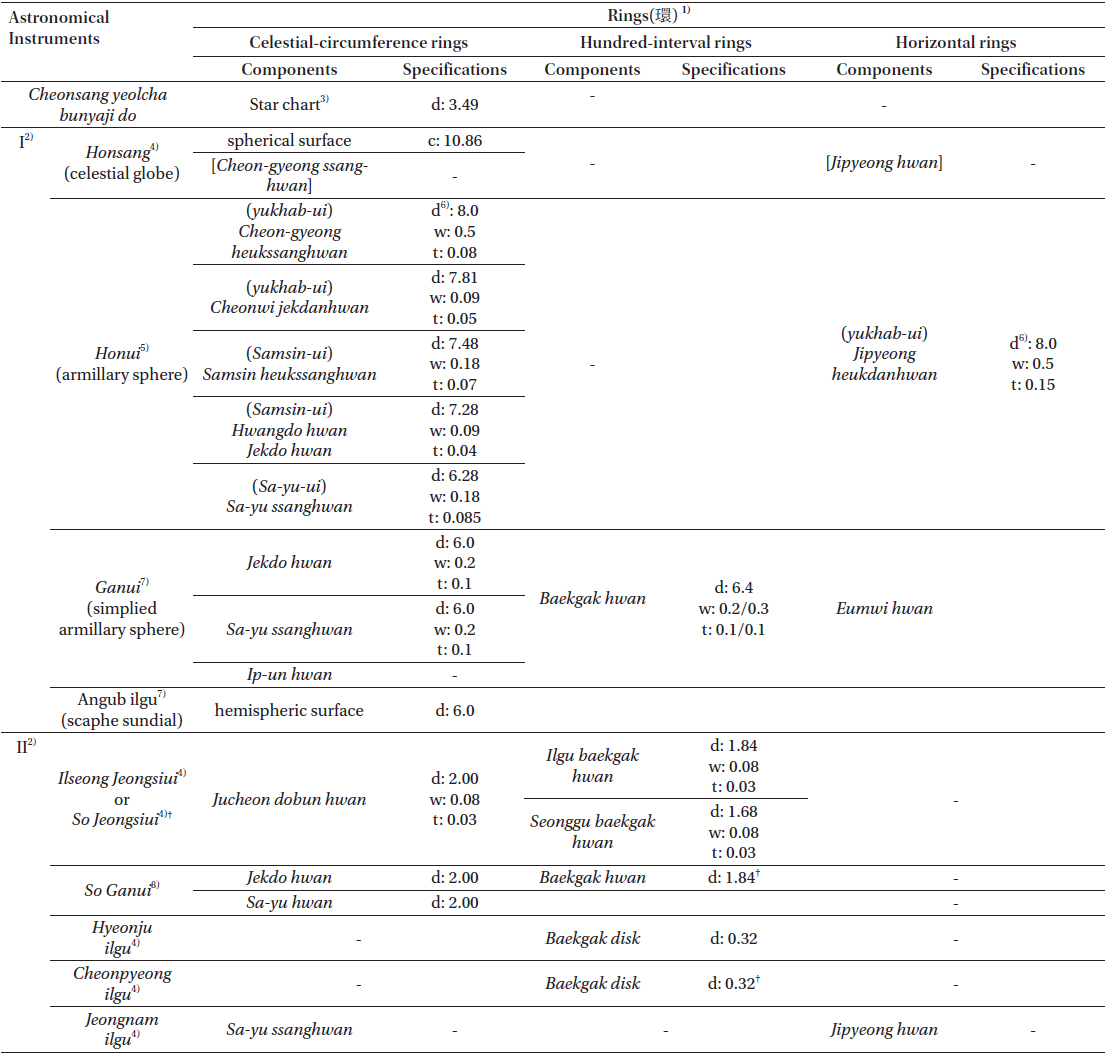
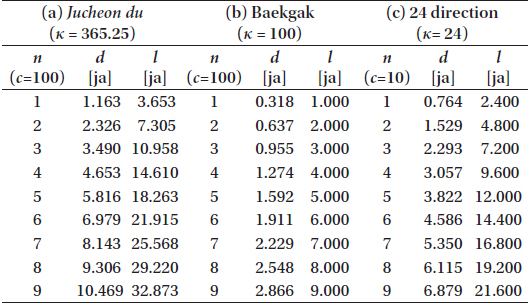
Most Joseonese astronomical instruments had various sizes of rings corresponding to the great circle of the celestial sphere. These rings were used to measure the position, time, and direction of celestial bodies, and those were known as Jucheon dobun hwan (a celestial-circumference degree-andfractions ring; abbreviated to celestial-circumference ring), Baekgak hwan (a hundred-interval ring), and Jipyeong hwan (a horizontal ring). The Jucheon dobun hwan divides the celestial sphere into 365.25 uniform parts according to the total days of a year. Occasionally, twenty-eight lunar lodges are marked together. This ring is either marked by a scale of 365.25 equal parts or marked twice by a scale of 182.6 equal parts. For example, the Jekdo hwan (an equatorial ring) of Ganui has twenty-eight lunar lodges with 365.25 ticks and its Sa-yu whan (a declination ring) marks the scale of 182.6 on the northern and southern half circles, respectively. Baekgak hwan is a ring carved with a twelve double-hour system and 100 gaks. However, after the introduction of the Shixian calendar, the time scale of a day was modified into 96 gaks. Also, 24 directions were marked on Jipyeong hwan.

Honcheonui is an astronomical instrument containing the most number of rings. It is believed that Honcheonui was made during the reign of King Sejong (世宗, 1419-1450) and is referred to in the “Compiled Description on the Shujing (書纂言)” by Wu Cheng (吳澄, 1249-1333) in the Yuan Dynasty. Honcheonui has a 3-layered structure of Yukhapui (a fixed celestial-coordinate part), Samsinui (a rotating three celestial body part), and Sayuui (a observational part). Each layer is composed of several single or double rings (Lee et al., 2010). The structrure of Honcheonui is complicated, as described above. However, Ganui (a simplified armillary sphere) was developed for a simpler structure. Moreover, So ganui was developed for a much simpler and smaller structure. The records of Ganui and Yangyi (仰儀, a scaphe sundial) are listed in the Yuan History’s (元史) section of Jega ryeoksangjib (諸家曆象集, collections of astronomy from all Chinese dynasties). According to this record, Ganui has a Baekgak hwan, Jekdo hwan, and Sa-yu ssanghwan. In particular, the Jekdo hwan rotates on the inner cross section of the L-shaped Baekgak hwan (Lee 1996). Most of the existing Angbu-ilgus (仰釜日晷, a scaphe sundial) from Joseon originated from the 17^th century or later. However, the prototype of the Angbu-ilgus from the early Joseon Dynasty is presumed to be a down-sized Yangyi according to the description of Xuanjiban(旋璣板, a pin-point plate) in the inscription of Angbu-ilgus written by Kim Don (金墩, 1385-1440).

As mentioned above, So ganui in the Sejong era is a simplified form of Ganui and it has three rings of Jekdo hwan, Baekgak hwan, and Sa-yu hwan. Even though their sizes are not known, according to the inscription of So ganui in the King Seongjong era, the diameters of Jekdo hwan and Sa-yu hwan are the same as those of 2 ja, which are based on the So ganui of the Sejong era (Lee & Moon 2004).

Lastly, Ilseong jeongsiui is a typical creative astronomical instrument and detailed dimensions are shown in the Sejong sillok. According to this record, the rings of Ilseong jeongsiui consist of a Jucheon dobun hwan (a celestial-circumference ring) and two Baekgak hwans (hundred-interval rings). Also, the record shows that So Ilseongjeongsiui was made to be almost similar to Ilseongjeongsiui. We can presume that the So Ilseongjeongsiui has three rings and the same dimensions.

Various small scale sundials were made in King Sejong’s era, for example, Hyeonju ilgu, Cheonpyeong ilgu (a rule-the-world sundial or a plummet sundial), and Jeongnam ilgu. According to Sejong sillok, there is a Baekgak disk with a diameter of 0.32 ja in the Hyeonju ilgu and the structure and dimension of Cheonpyeong ilgu are similar to Hyeonju ilgu. Cheonpyeong ilgu, which was developed to determine the time in the middle of horse riding, has a Baekgak disk similar to Hyeonju ilgu. Unlike Hyeonju ilgu, it has irrigable pools at both the south and north sides and a rope attached to the top of the post in order to grip it while winding a rope around a wrist. Jeongnam ilgu measures the time using Sa-yu ssanghwan (a declination double ring). However, the exact dimensions of Sa-yu ssanghwan are not known.

Table 1 shows the dimensions of astronomical instruments according to the category of restored astronomical instruments (I) and creative astronomical instruments (II). The rings of each astronomical instrument are divided into Jucheon dobun hwan (celestial-circumference), Baekgak hwan (hundred-interval rings), and Jipyeong hwan (horizontal ring). In this table, the unit length of specifications is ja (refer to Section 3.2). The star charts of Cheonsang yeolcha bunyajido and Honsang are classified as celestial-circumference rings and the Baekgak disks of Hyeonju ilgu and Cheonpyeong ilgu are classified as hundred-interval rings for convenience.

In ancient China, the du in the celestial-circumference degree is a unit of length rather than of angle. This unit has been used in astronomical instruments (Zhang 2000). According to Zhoubi suanjing (周脾算經, arithmetic classic of circles and gnomons), the circle of diameter, 121.75 ja, has a circumference of 365.25 ja which makes 1 du equal 1 ja. According to this method, the circle is equally divided by using the celestial-circumference degree, and the ratio of the circumference used was 3. Thus, the scales of a circle or a sphere were marked as angular distance.

While the ratio of circumference was 3 in Zhoubi suanjing, Liu Hui (劉徽) from the Wei Dynasty (魏, 220~265) of China used 157/50(=3.14) and Zhao Chong Zhi (趙冲之, 429~500) of the Liu’s Song (劉宋, 420~479) used 3.1415926 (Needham 1959, Kim 2006). It seems that the ratio ocircumference varies depending on the precision of the scales and the convenience of calculation. However, as astronomical instruments require precise measurement of the position of the celestial body, it is believed that the value of 3.14 was used in marking the scales on the circumferences.

Similar to China, the units of length used in Joseon are jang, ja, chi, pun, li, and ho, where, 0.1 jang = 1 ja = 10 chi = 100 pun = 1000 li = 10000 ho. In particular, Ju cheok(周尺, a royal standard ruler) was used in Joseon and 1 ja of this ruler was 207 mm (Nam 1995). In contrast, 1 ja of the astronomical instruments from China was 245 mm (Kim 1993, Lee et al. 2011)

As shown in Fig. 1, it is assumed that the scales of a circle, sphere, or ring in the astronomical instruments of China or Joseon were inscribed by dividing the circumference equally with the integer multiple of unit length. First, if we designate the circumference as l, the ratio of circumference as π, and the ratio of the division as ĸ, the diameter of a ring can be expressed as follows:

where a is the size of the unit scale.

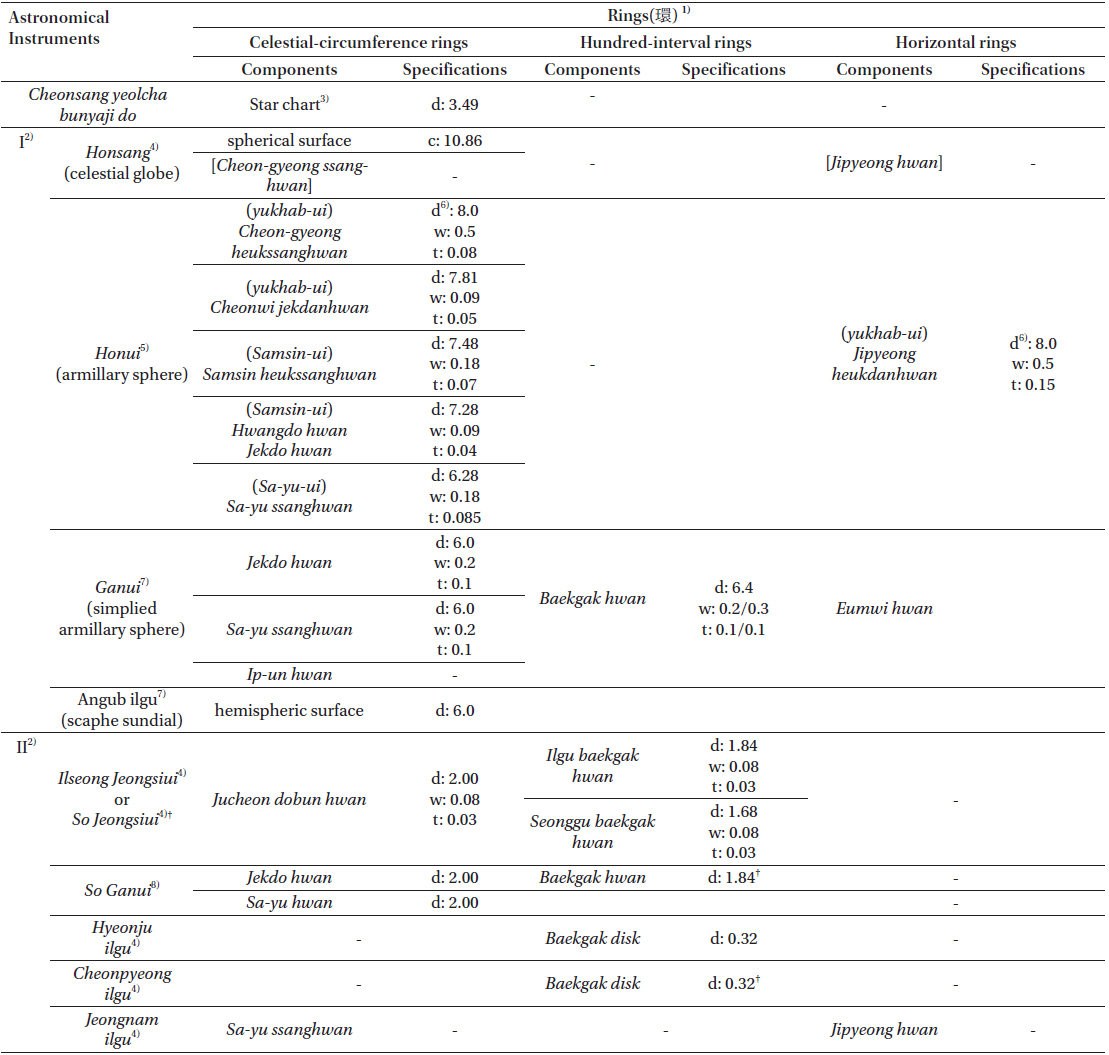
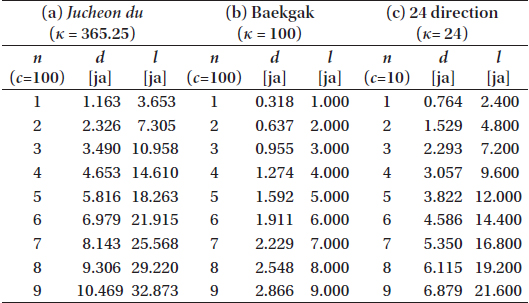
Although it is possible to express l or d in the unit of ja, a can have the unit of chi or pun. If n is a positive number and c is a conversion constant, it is possible to express n as n = n/ c. For example, if c = 1, the unit of n is ja, and if c = 100, the unit of n is pun. If the unit length of a du from Jucheon du (the celestial-circumference degree) or a gak from Baekgak (the hundred-interval) is 1 chi (c=10), the diameter and circumference of a circle can be obtained by multiplying 10 to the value of Table 2.

Although there is no record on this in Taejo sillok (Veritable Record of the King Taejo), the original Cheonsang yeolcha bunyajido appeared to have been made at the end of the 4^th year of Taejo (1395). Using the replica in KASI, the diameter of the coordinate circle of Jucheon dobun was measured to find the north-south diameter of 723 mm. When this value is converted using the royal standard ruler of the Sejong era, the diameter is about 3.49 ja. Furthermore, the Chunyou star chart (淳祐天文圖) in China, which has a circular star chart on the top, was made 150 years earlier than the Cheonsang yeolcha bunyajido. According to the rubbing of the Chunyou star chart at KASI, the measurements of the north-south diameter from the coordinate circle, on which Jucheon du is marked, is 844 mm, which is 3.44 ja in units from old China.

The value of 3.490 ja in Table 3 is quite similar to the diameter of the coordinate cicle with n = 3 in Jucheon du’s column of Table 2. Although the physical sizes of both star charts are different from each other, it is clear that the sizes of those charts in units of ja are similar and that the diameter of the star chart in Cheonsang yeolcha bunyajido is 3.49 ja based on the royal standard ruler of the Sejong era. In the two star charts mentioned above, the total degree of Xu lunar lodge (虛宿) is about 9 1/4 du. However, it is actually 9 du. Therefore, the circumference can be uniformly divided into 365 parts rather than 365.25 parts and the circumference is calculated to be about 10.95 ja based on the scale of 3 pun per 1 du.

In Cheonsang yeolcha bunyajido, the center of the chart is the north pole and the radius of the coordinate circle is the boundary of seeing a star at an observatory. Thus, that boundary depends on the latitude (φ , the altitude of north pole) of the observer. The boundary circle indicates – (91.3125 – φ ) du in the declination and (182.625 – φ ) du in polar distance. In Table 3, the radius of equatorial circle is about 1.08 ja and the radius of the coordinate circle is 1.745 ja. Hence, φ is calculated to be (182.625 – 91.3125) duㆍ(1.745/1.08) = 35.09 du. Converting this value into a 360˚system gives us 34.58˚, which is close to the latitude of Yangcheng(陽城) of the Zhuo Dynasty (周) or the current Dengfeng(登封) where the Zhougong cejing tai (周公測景 臺) and Guanxing tai (觀星臺) are located. In Cheonsang yeolcha bunyajido, 91.3125 du corresponds to 1.08 ja, so 1 du in declination is about 1.2 pun for scale marking. On the contrary, if we fix 1 du as 1.2 pun in declination, the radius of the equatorial circle is about 1.096 ja while that of the coordinate circle is 1.758 pun, which shows a difference of about 1.5 pun each.

Ahn (2010) suggested that the Cheonsang yeolcha bunyajido was made according to the method described in Tianwen zhi(天文志, the treatise on astronomy) of Xin tangshu(新唐書, the new book of Tang history). If the star chart followed the method of Xin tangshu, the right ascension should have been marked by 3 pun per 1 du on the basis of the circumference of the coordinate circle and polar distance being 1.2 pun per 1 du or 6 pun per 5 du, which is like a polar coordinate with the origin as the north pole. According to Xin Tangshu, the ruler made the skin of a bamboo tree have 147 scales from a hole at one end of it (Ahn 2010). 147 scales of that ruler agrees well with those of the radius of the coordinate circle of Cheonsang yeolcha bunyajido (181.625 du – 35 du=146.625 du).

According to Sejong sillok, the circumference of Honsang is 10.86 ja, as shown in Table 1. However, the circumference of a circle with n=3, as shown in the Jucheon du column of Table 2, is 10.958 ja. If we assume that the record of Sejong sillok is a typo of 10.96 ja (Han et al. 2001), the diameter of the coordinate circle in Cheonsang yeolcha bunyajido is the same as that of Honsang. The difference from Cheonsang yeolcha bunyajido is that Honsang is 3 pun per 1 du in the declination scales, which are similar to the right ascention ones. If the bamboo ruler described in Xin Tanshu(新唐書) was used to put stars on the surface of Honsang, it would have had 147 scales of 3 pun and not 1.2 pun. Sejong sillok described in Honsang as being installed with Honui in the pavilion and powered by water force. The diameter of Honui is more than twice of the diameter of the Honsang shown in Table 1, so the volumes differ by 8 times or more.

The royal standard ruler did not exist in the Goryeo Dynasty and it was newly introduced in the Sejong era of the Joseon Dynasty (Lee 2001). This does not agree with the date of Cheonsang yeolcha bunyajido of Taejo era, the 228^th Korea national treasure. In order to find out whether this treasure is from the Taejo era or not, or whether a ruler similar to the royal standard ruler was used or not, archeological study is necessary. It is well-known that stone carved astronomical charts were built in the Sejong era (Koo 2007). The epilogue of Jega ryeoksangjib said that an astronomical chart in the Sejong era was inscribed to a stone based on the Shoushi calendar. If so, at that time, the new engraving of Cheonsang yeolcha bunyajido might be reproduced by the originals. In Cheonsang yeolcha bunyajido, the width of stele in the Taejo era was 122, which is 8 cm wider than that of the Sukjong era (the 837^th Korea Treasure). Its configuration of the planisphere and the inscription are not in the middle of the stele and leftward drawing(Jeon et al. 1984).

Hyeonju ilgu and Cheonpyeong ilgu are down-scaled astronomical instruments from the Sejong era and could be classified as equatorial sundials. As indicated in Table 1, there is a Baekgak disk with the diameter of Hyeonju ilgu being 0.32 ja. The diameter of this disk corresponds with n=1 in the Baekgak column shown in Table 2 where 1 gak is 1 pun. There is an artefact known as Hyeonju ilgu and the diameter of its Baekgak disk is 7.1 cm (Song et al. 1994), which is 0.34 ja in the unit of the royal standard ruler from the Sejong era. Assuming the ratio of circumference as 3 rather than 3.14, this can be interpreted to be the diameter of a circle with 1 gak per 1 pun.

Applying Equation (1), we can predict whether the ratio of circumference applied to astronomical instruments is 3.14 or 3. If we let π₁ and π₂ be 3 and 3.14, respectively, and the corresponding diameters based on Equation (1) are d₁ and d₂ , the difference of diameters is calculated as follows:

Where, π₂^-1− π₁^-1=-14.86×10⁻³. If we mark the scale of 100 gak (κ =100), Δd ≈ −1.49_{n⋅ c}⁻¹. In the case c is 100, Δd becomes -1.49 pun (about 3 mm) per unit scale of 1 pun. However, when the unit of 1 gak is chi or ja ( c is 10 or 1), becomes -1.49 chi (about 3 cm) or -1.49 ja (about 30 cm). Thus, it is difficult to build astromical instruments based on the circular constant of 3.

If we let π₁ and π₂ be 3.14 and 3.1415926, respectively, and the corresponding diameters are d₁ and d₂, assuming that Jucheon du is marked on the circumference, Δd ≈ −5.89×10⁻² n⋅c⁻¹ according to Equation (2). Although c is 1, Δd has little discrepancy of -5.89 pun (about 12.2 mm) per unit scale of 1 ja. Since the difference is excessively small, it is speculated that astronomical instruments are built based on the circular constant of 3.14.

Jeongnam ilgu is also one of the down-scaled sundials and has a special shape of sundial, which was described in Sejong sillok. Sa-yu hwan, half Baekgak hwan, and Jipyeong hwan, which are rings of Jeongnam ilgu, have a scale of the celestial-circumference degree, a hundred-interval, and 24 directions, repectively. Though the dimension of these rings was not recorded, it is estimated that the diameter of Jipyeong hwan is greater than 1.0 ja and the diameter of half Baekgak hwan is between 1.0 ja and 0.9 ja, while the diameter of Sa-yu whan is between 0.9 ja and 0.67 ja.

The length of the bottom plate of Jeongnam ilgu is 1.25 ja and the distance between the two posts in the south and north is about 1.0 ja. Because the summer solstice is the longest day, half Baekgak hwan is aligned along the line of the summer solstice and the scales of 100 gak are marked on it. The heights of the northern post and southern post are 1.1 ja and 0.59 ja, respectively. The inclined axis of Sa-yu whan passes through two posts, and the intersection occurs at the height of 0.99 ja in the northern post while that occurs at 0.21 ja in the southern post. The intersection point of the northern post is 0.78 ja higher than that of the southern post. The latitude of Hanyang (the old name of Seoul), the capital of Joseon, was set as 38 du (37.45°) while the tan (37.45°) was about 0.766. In other words, the distance between the two posts and the height difference between the two intersections of the axis and post were designed to closely correspond to the latitude of Hanyang. While it is not certain how they determined 0.766 in those days, it can be estimated from the table in Lizhi (曆志, Treatise of the Calender) of Mingshi (明史, History of Ming Dynasty). According to Mingshi, values corresponding to the adjacent leg and opposite leg of a right triangle are obtained using Hushi geyuan (弧矢割圓, Calculation of the arc and sagitta in the secant of the circle ) and Zhehui (折會術, Trapezium Method of the secant of the circle ) of Shen Gua (沈括, 1031 - 1095). Based on these, the ecliptic opposite leg (黃道半弧弦) is 36.7486 du and the ecliptic adjacent leg(黃道大股) is 48.5316 du. Thus, the ecliptic tangent is 0.7572.

The arm of the Baekgak disk of Hyeonju ilgu is slantly fixed to the right triangle shaped socket which soars from the bottom (Song et al. 1994). If the lengths of the adjacent leg and opposite leg in the right triangle are 3 and 4, respectively, the slanting angle will be tan^-1(4/3)=53.13° (53.9 du). Fortunately, it is similar to the intersection angle between the horizontal plane and the equatorial plane, which is about 52.55° (53.3 du) at Hanyang. For example, if we set the adjacent leg and the opposite leg of the socket to 0.12 ja and 0.16 ja, respectively, the Baekgak disk of Hyeonju ilgu could be installed to fit the latitude of Hanyang.

Various astronomical instruments were made through the construction of an observatory during the Sejong era. Some of these instruments were replicas of astronomical instruments from old Chinese dynasties while others were newly developed instruments. There are circular components in these instruments indicating the great circle of the celestial sphere, and there are scale inscriptions of the celestial-circumference degree, a hundred-interval, and 24 directions. Circles, spheres, and rings having these scales do not have arbitrary sizes, but specific sizes of circles, which could be divided into equal parts of 365.25, 100, or 24. That is, the angular distance on the circumference of a circle is subdivided instead of the angle itself in order to mark scales.

In this paper, simple cases of marking scales in integer multiple unit intervals were analyzed through the articles from the Joseon dynasty and the extant artifacts of astronomical instruments. The star chart of Cheonsang yeolcha bunyajido in the early Joseon Dynasty and the Honsang of Sejong era drew the celestial-circumference degrees on a circle whose circumference is 10.96 ja in a unit scale of 3 pun per 1 du. While the declination is on a scale of 1.2 pun per 1 du in the star chart of Cheonsang yeolcha bunyajido, the declination of Honsang is on a scale of 3 pun per 1 du. In this analysis, it was found that the planisphere of Cheonsang yeolcha bunyajido was designed with a royal standard ruler. If the roral standard ruler did not exist in the Taejo era of Joseon, the 228^th national treasure of Cheonsang yeolcha bunyajido might be a stone copy of the original made after the Sejong era.

According to the record, Hyeonju ilgu and Cheonpyeong ilgu had a Baekgak disk with a diameter of 0.32 ja, of whose circumference divided hundred ticks by 1 gak per 1 pun and corresponds to the size of the existing artifacts. Although there is no record about the dimension of rings in Jeongnam ilgu, it is estimated that the diameter of Jipyeong hwan is greater than 1.0 ja, the diameter of half Baekgak hwan is between 0.9 ja and 1.0 ja, and the diameter of Sa-yu whan is between 0.67 ja and 0.9 ja. There is a right triangle socket for the Baekgak disk in the existing artifact of Hyeonju ilgu, making it possible to build the Baekgak disk to fit the latitude of Seoul by using the Pythagorean’s theorem.