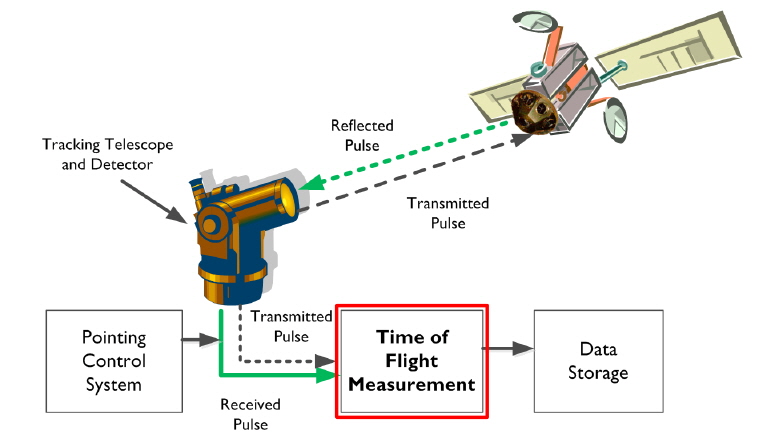
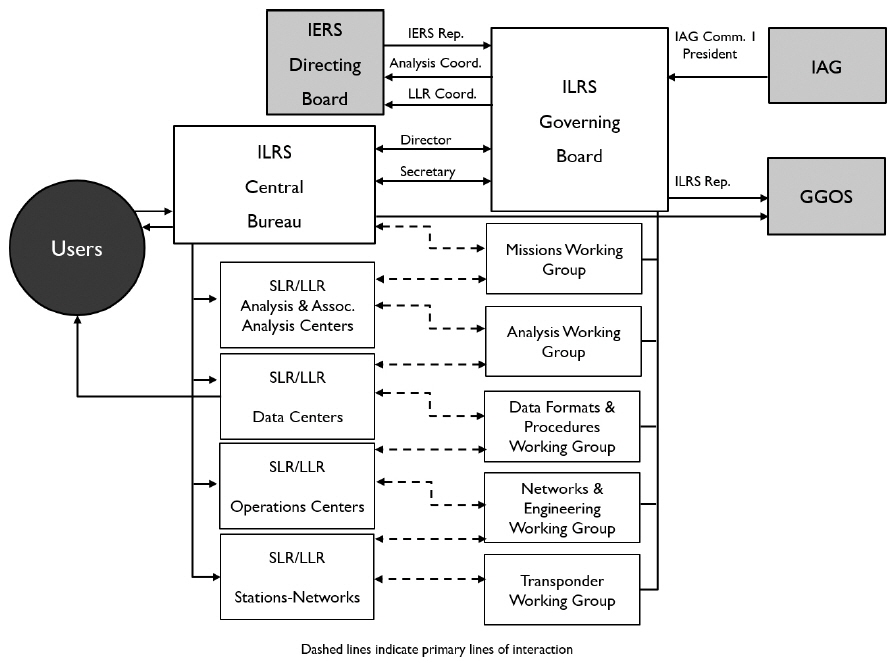
The Science and Technology Satellite (STSAT)-2C was developed by the Satellite Technology Research Center (SaTReC) of the Korea Advanced Institute of Science and Technology (KAIST) and launched by Korea’s first launch vehicle, the Korea Space Launch Vehicle (KSLV)-1, on January 30, 2013. The purposes of the STSAT-2C mission are to test the KSLV-1 and develop a small spacecraft (Kang et al. 2014). The STSAT-2C spacecraft is equipped with a laser retro-reflector array for satellite laser ranging (SLR), and has been tracked by the global network of SLR stations (International Laser Ranging Service - ILRS) since March 29, 2013 (Pearlman et al. 2002). SLR is the most precise technique for measuring the distance between a satellite and the tracking station and the ILRS manages operation and data processing of SLR. Fig. 1 illustrates the concept of SLR and Fig. 2 shows the organization of ILRS. In Korea, mobile and stationary systems for SLR tracking have been developed since 2008 by Korea Astronomy and Space Science Institute (Lim et al. 2010; Seo et al. 2010; Jo et al. 2011; Lim et al. 2011; Nah et al. 2013). The mobile SLR system development was finished and it delivers adequate ranging observations with a few mm precision (Park et al. 2012; Choi et al. 2014). The ILRS associate analysis center is also operated by same institute (Kim et al. 2012, 2013b).
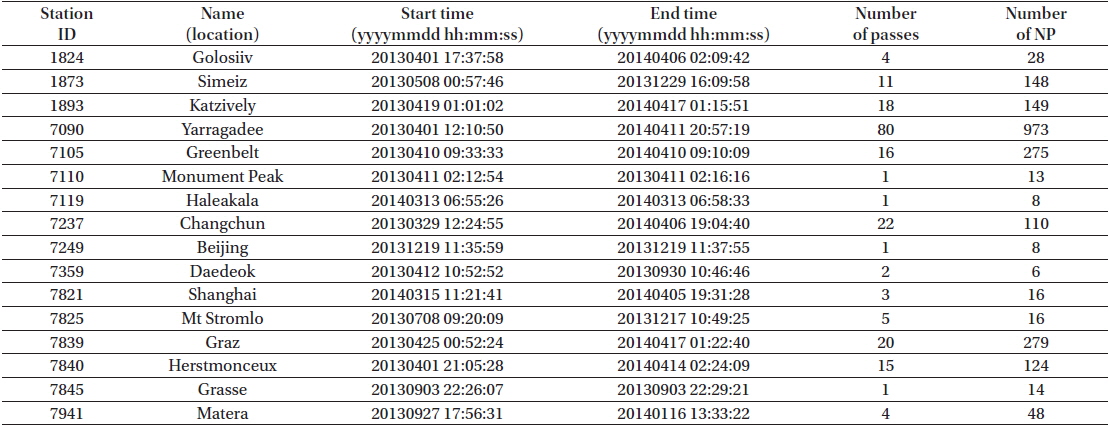
The main SLR application of STSAT-2C is precise orbit determination (OD). The OD analysis with SLR observations for STSAT-2C can contribute to research on extremely low orbital environments (~300 km) and modeling accuracy assessment by using radial orbit error analysis. Therefore, it is an important issue to secure sufficient SLR tracking data. The SLR tracking statistics during a 12-month follow-up period are presented in Table 1. The total passes and normal point (NP) observations during the last year are 204 and 2,215, respectively. The acquired amount of NPs is very low and sparse compared to the other laser-tracked low-earth orbiting satellites due to inexact orbit predictions for SLR tracking. For example, in the first week of April 2014 alone, the Jason-2 mission achieved 240 passes and 4,482 NPs. In this light, the SLR tracking for the STSAT-2C can be regarded as extremely sparse measurement conditions. As the STSAT-2C was utilized for successful orbit injection of KSLV-1, it was assigned a highly elliptical orbit (300 km – 1,500 km). While a GPS-based technique is generally used for positioning of non-geodetic satellites, radar-based two-line element (TLE) is utilized for orbit acquisition of STSAT-2C. Thus very poor orbit predictions have been provided for STSAT-2C for SLR tracking. As a result, it can be tracked only when the satellite is in a visible period. SLR tracking and OD using SLR observations are very challenging issues in the SLR community. Although a SLR-based strategy is a baseline for STSAT-2C OD, providing steady results has proved difficult.
[Table 1.] ILRS tracking statistics for STSAT-2C (2013/03 - 2014/04).
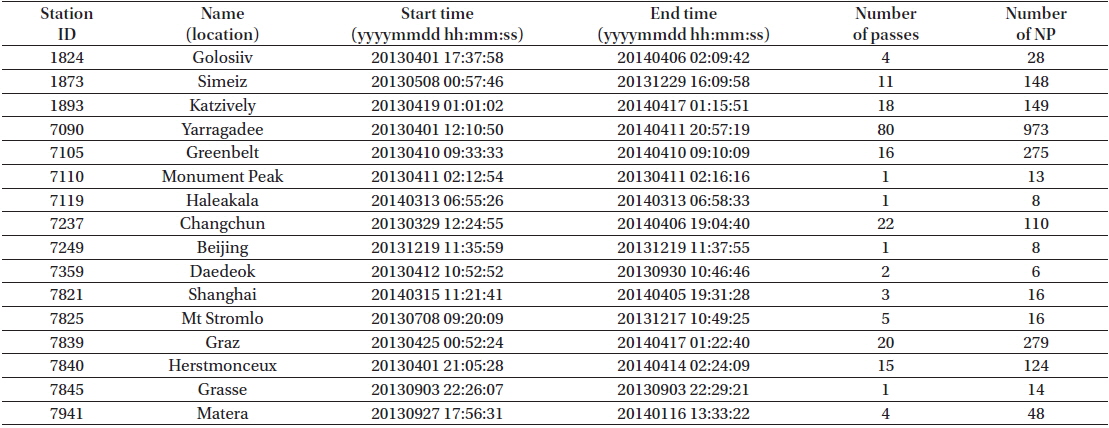
ILRS tracking statistics for STSAT-2C (2013/03 - 2014/04).
Lee & Alfriend (2007) pointed out that an inaccurate initial orbit and sparse measurements can result in unstable solutions of orbit estimation. To overcome this problem, various estimation algorithms such as unscented transformation and a particle filter have been suggested by Lee & Alfriend (2007), Park et al. (2010), and Kim et al. (2011, 2014b). Another way to avoid sparseness is to use a short-arc estimation strategy. Although this approach does not guarantee the best orbit accuracy, it can give the results of orbit estimation and prediction under very sparse measurement conditions. It has been demonstrated that the short-arc approach is very helpful for OD and prediction of low-Earth orbiting (LEO) objects including space debris (Sang & Bennett 2014; Bennett et al. 2015). From a practical perspective, the short-arc OD approach in a sparse measurement condition is more advantageous than a new estimation strategy.
Kim et al. (2013a, 2014a) have implemented an orbital analysis for a few arcs of STSAT-2C using a short-arc approach. It has been reported that OD using SLR observations for STSAT-2C can be successfully accomplished despite the very sparse measurement condition. In the current study, almost all passes of one year were included in a short-arc OD strategy and the results were analyzed by post-fit residuals. For some periods, orbit overlaps results are investigated for the orbit quality check. As the estimation intervals of atmospheric drag and empirical acceleration affect the convergence property of OD for STSAT-2C using short-arc, a non-regular daily-based processing strategy with variable estimation intervals is applied. The aim of the current study is to obtain successful OD results for STSAT-2C using SLR short-arcs in order to improve the orbit predictions for SLR tracking. Section 2 summarizes the OD strategy and software settings and Section 3 describes the results of the post-fit residuals and orbit overlaps of short-arc OD. Section 4 gives conclusions.
2. ORBIT DETERMINATION USING SLR DATA
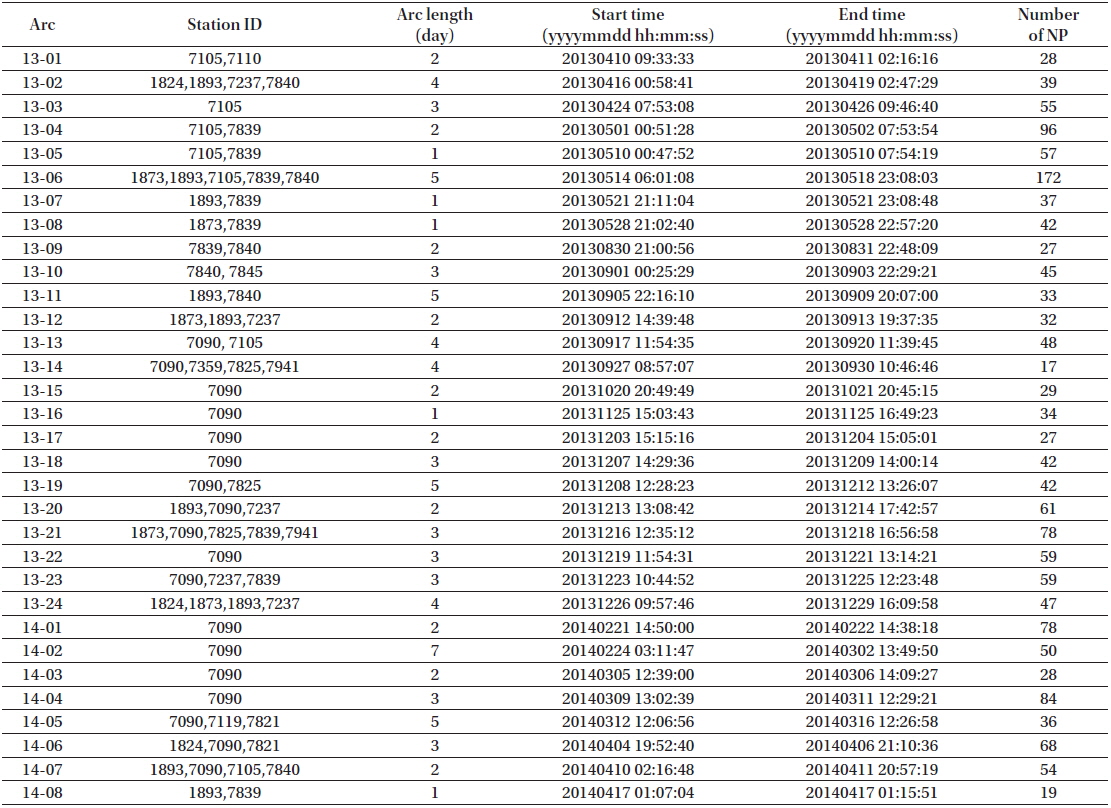
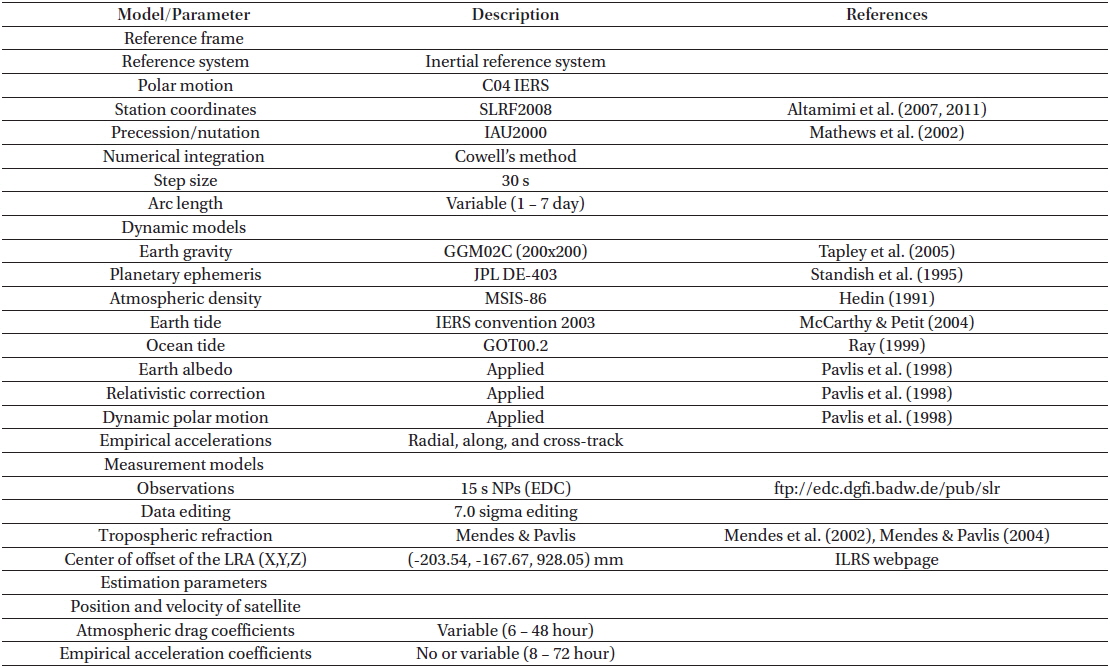
In this section, the strategy for OD of STSAT-2C using SLR data is summarized. The NASA/GSFC GEODYN II software is used for SLR data processing (Pavlis et al. 1998). The arcs for OD are prepared using a few passes with a minimum number of measurements for the parameter estimation. In this study, the existence of 10 NPs in one arc was adopted as a minimum condition for arc length determination. The final selected arcs for OD are presented in Table 2. The specific modeling and the estimation parameters are presented in Table 3. The arc length chosen for the OD was changed by the observation conditions, which originated from the number of NPs and the continuity of passes. The shortest and the longest arc length are 1 and 7 days, respectively. The number of stations used for the analysis also differs for each arc. In Table 2, some arcs comprised observations from only one station, given that most of the SLR observations for the STSAT-2C were actually obtained by only one station in that period. Generally, such passes must be extended to include the data from other stations, or to be rejected from the OD process. However, to retain as many OD arcs as possible for the study, the short arcs recorded by only one station were included. Short arcs obtained by only one station are commonly accepted for OD of STSAT-2C, and therefore it is reasonable to include these arcs in the analysis.
[Table 2.] Summary of the STSAT-2C arcs (2013/03 ? 2014/04).
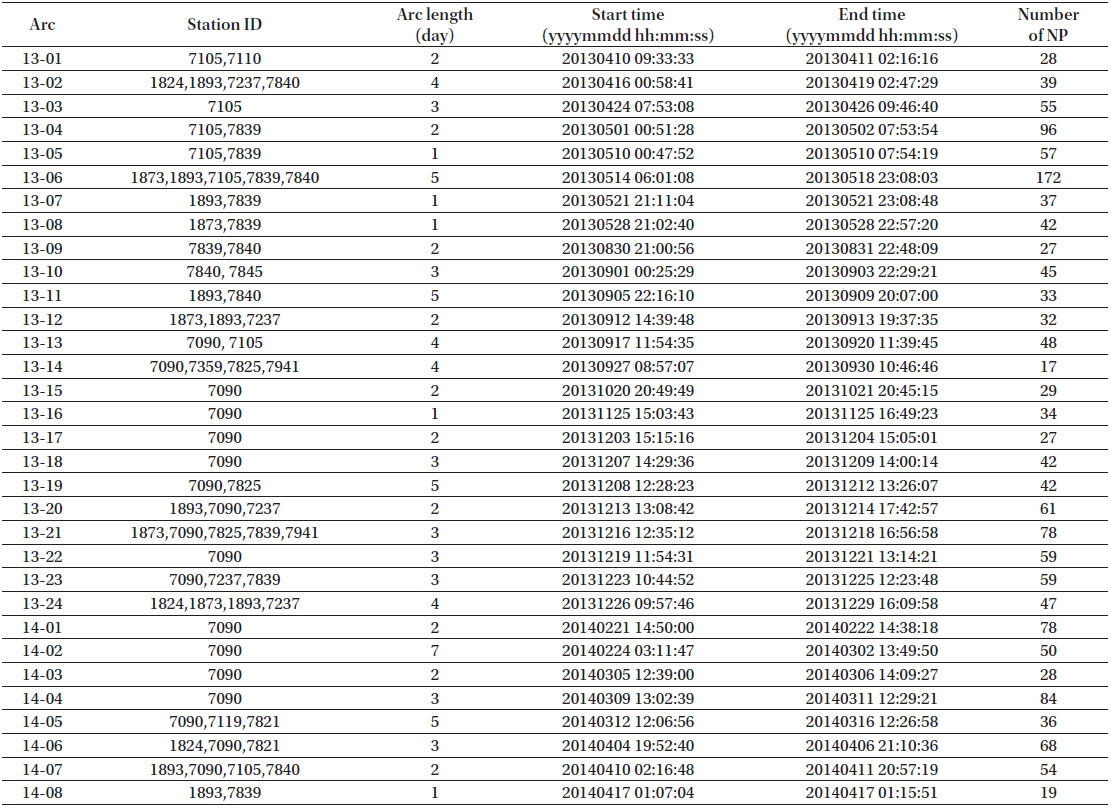
Summary of the STSAT-2C arcs (2013/03 ? 2014/04).
[Table 3.] Details of models and estimation parameters for STSAT-2C orbit determination.
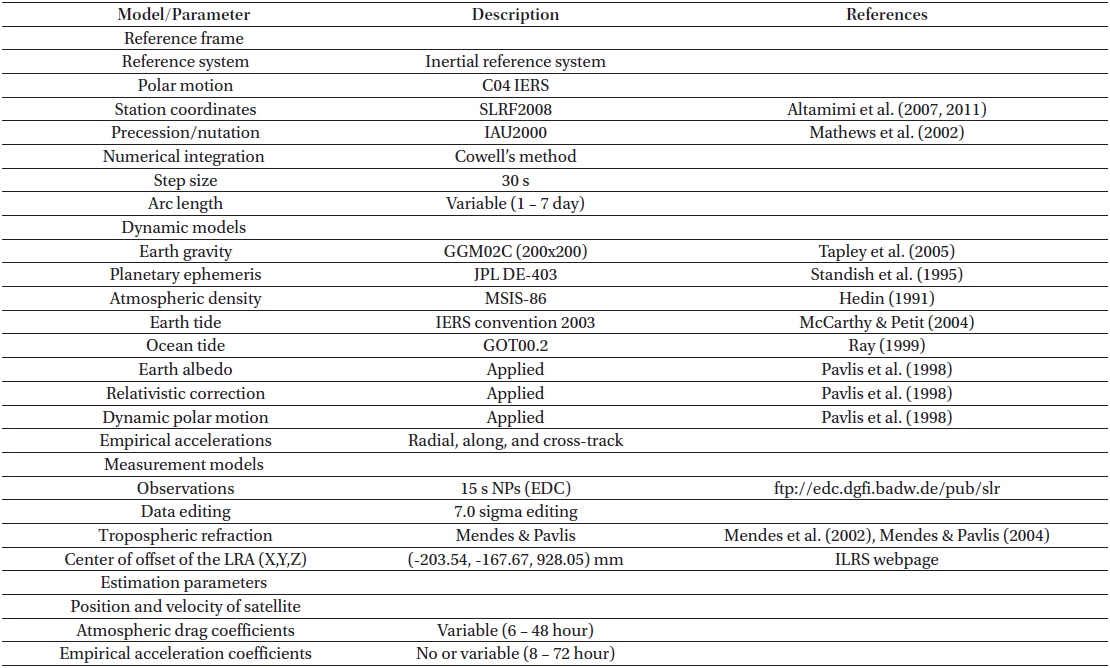
Details of models and estimation parameters for STSAT-2C orbit determination.
The estimation frequency of the parameters such as the drag coefficients and the empirical acceleration coefficients can affect the precision of the OD for LEO satellites. For Starlette, 24 hour and 12 hour intervals are used for drag coefficient estimation (Lejba et al. 2007; Lejba & Schillak 2011). Jeon et al. (2011) and Jagoda & Rutkowska (2013) use 8 hours and 7 days for the OD of Starlette. Lejba & Schilliak (2011) demonstrated that more frequent estimation of the empirical acceleration parameters can improve the precision of the post-fit residuals of Starlette and Stella. However, in very sparse measurement conditions, convergence of estimation by the least-squares batch cannot be guaranteed if the number of estimation parameters increases. For the sparse data distribution of STSAT-2C some arcs necessitate the use of only specific intervals for convergence. Improvement of the tracking geometry by expanding the arc length is an alternative except for the cases where the observed arcs of orbit are separated by large time-gaps. In this study, a suitable selection strategy of the estimation intervals is therefore accomplished for every arc including a tuning process. Five different intervals are used for the drag coefficient estimation: 6, 8, 12, 24, and 48 hours. For the empirical acceleration coefficients 5 estimation intervals are applied: 8, 12, 24, 48, and 72 hours. In order to achieve stable convergence, the empirical acceleration coefficient are not estimated for several arcs. Generally, empirical acceleration parameters are estimated to compensate incomplete modeling errors of LEO satellites. However, in the present study, they are used as tuning parameters due to very sparse measurements. As a consequence, different OD strategies were utilized for each arc in order to overcome the inconsistent conditions created by the sparse measurements of STSAT-2C.
To eliminate outlying range residuals, a 7.0 sigma editing strategy is applied; in contrast the common sigma criterion in the analysis of LAGEOS and ETALON observations is 3.0 or 3.5 (Kim et al. 2013b). The relatively large sigma editing value is used to prevent failure of least-squares estimation due to a lack of observations. The center of the offset correction of the laser retro-reflector array for STSAT-2C applied in the OD analysis is given at the ILRS web page and is presented in Table 3. As the OD characteristics and results for STSAT-2C are very sensitive to the initial conditions and to the estimation configuration, an extensive iterative process including manual tuning was required to find the prior initial values and for proper selection of the estimation parameters. The prior value of the initial orbit was first obtained from the predicted orbits by the KAIST prediction center (KAI), the main provider of STSAT-2C orbit predictions. Due to the low accuracy of the TLE-based KAI’s prediction, manual tuning was performed to reduce errors at the first iteration of the OD analysis. The successfully determined orbital parameters of the first arc are used as the initial conditions for the consecutive arc.
In this section, the OD results and the orbit quality assessments are investigated. The post-fit residuals, which show how well the estimated orbit fits the SLR measurements, and orbit overlaps, which demonstrate the quality and the consistency of the determined orbits, are presented.
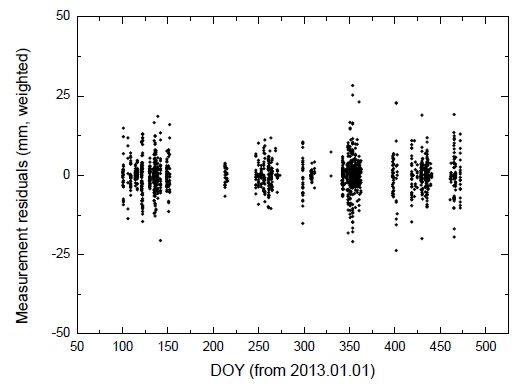
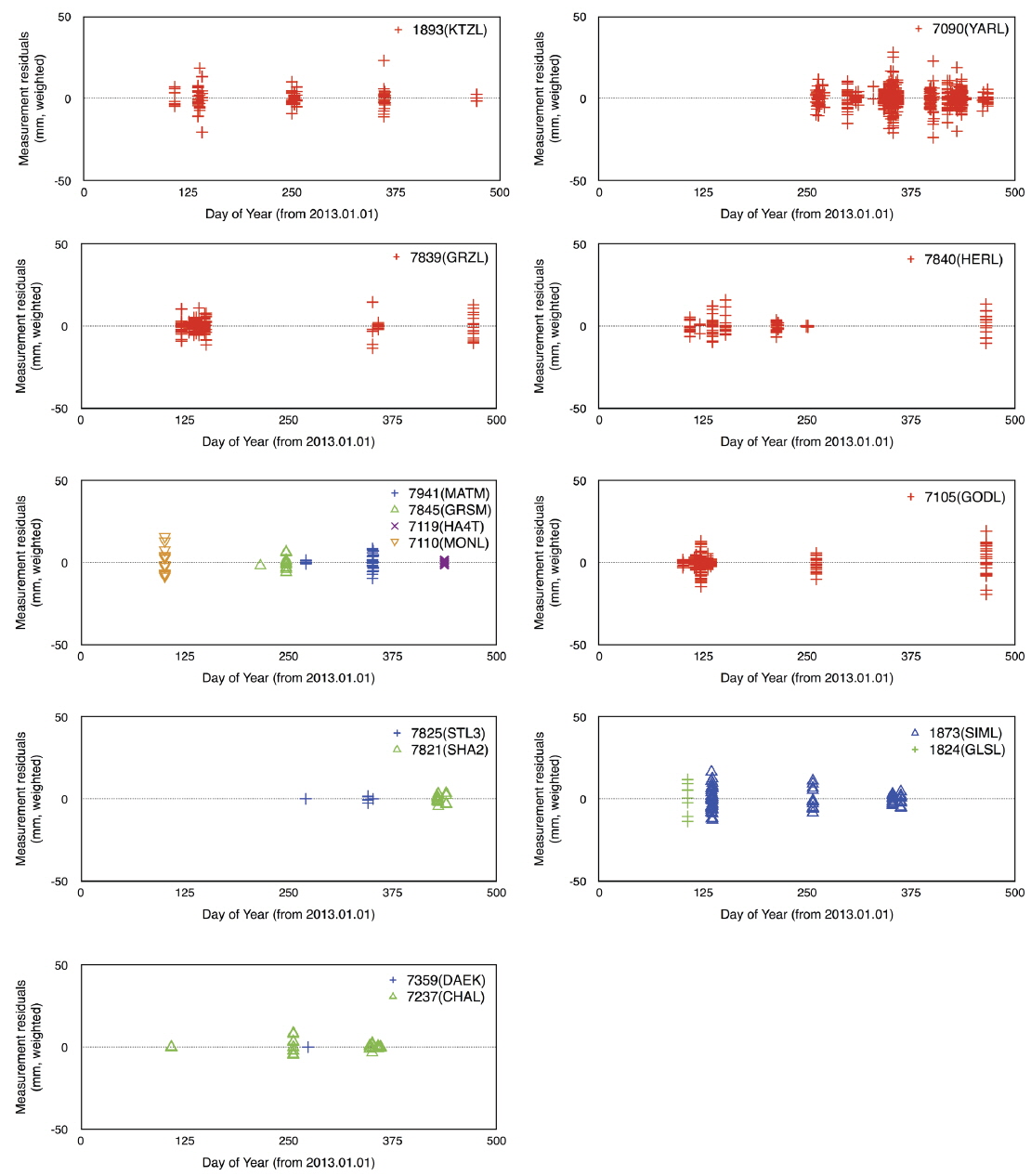
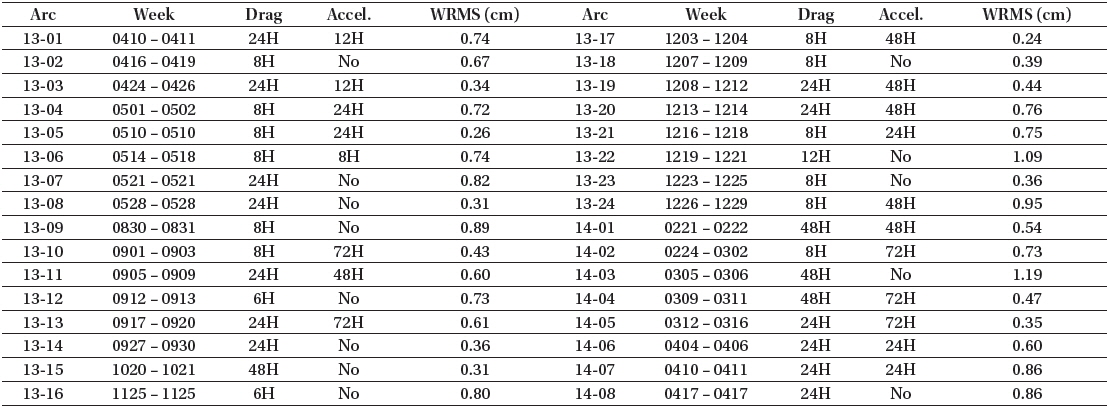
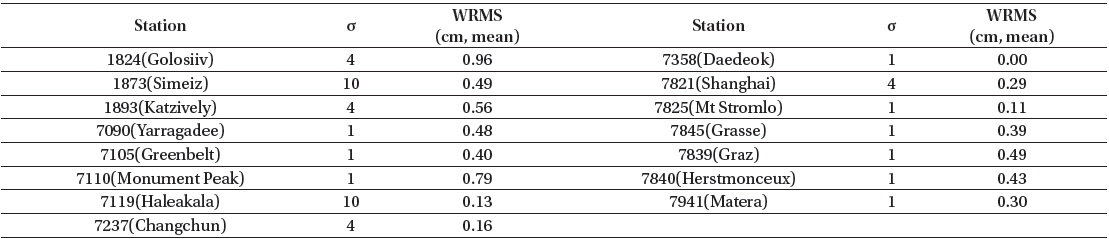
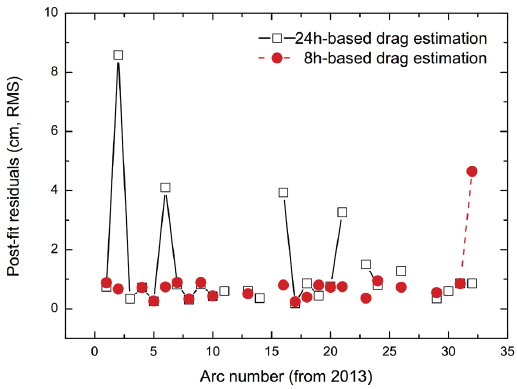
For STSAT-2C, the determined weighted root mean square (RMS) values of the post-fit residuals for 2013 and 2014 are 0.60 and 0.70 cm, respectively. The results are presented in Table 4 and Fig. 3. Table 4 shows the post-fit residuals and the coefficient estimation intervals for STSAT-2C OD. The weighted RMS of the post-fit residuals for most arcs is less than 1 cm. Fig. 3 shows the residuals of the weighted measurement residuals according to the day of the year from January 1, 2013. Fig. 4 and Table 5 show the residuals of each station for the total period. Fig. 4 displays the station residual precision of STSAT-2C OD. In Table 5, the mean measurement residual (weighted RMS) for each station and its observation-weighting are summarized. These residuals do not indicate the absolute precision of stations because each station has a different weight value by observation-weighting sigma (σ) and the number of observations is quite unbalanced. The value of σ is determined by the tracking performance of each station. First, ILRS core stations, which have a stable NP quality and a long-term tracking history, have σ=1. Next, the weighting σ of other stations is assigned as 1, 4, or 10 according to the ILRS station quality report. If the observation-weighting value is above 1 for a station, SLR data of that station are underweighted in OD as much as the amount of the σ-value. Fig. 5 shows the effects of drag estimation frequency through the results of the post-fit residuals. Except some arcs that have no converged results, 8 hour-based results generally show better precision than 24 hour-based results. However, this also shows that the 8 hour-based strategy for drag coefficient estimation sometimes fails to obtain converged results. This is attributed to the sparse measurement condition of STSAT-2C giving an unstable estimation solution due to the increased number of estimation parameters.
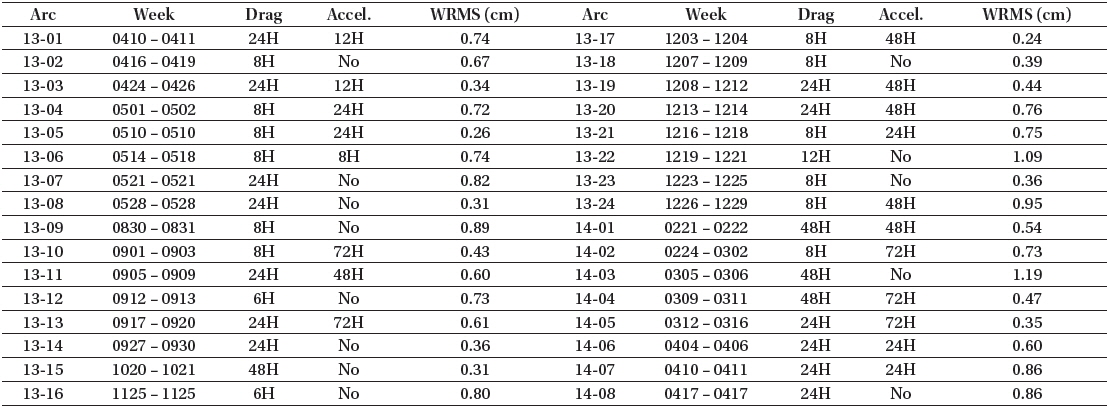
The post-fit residuals and coefficient estimation intervals for STSAT-2C orbit determination.
[Table 5.] Measurement residuals of each station.
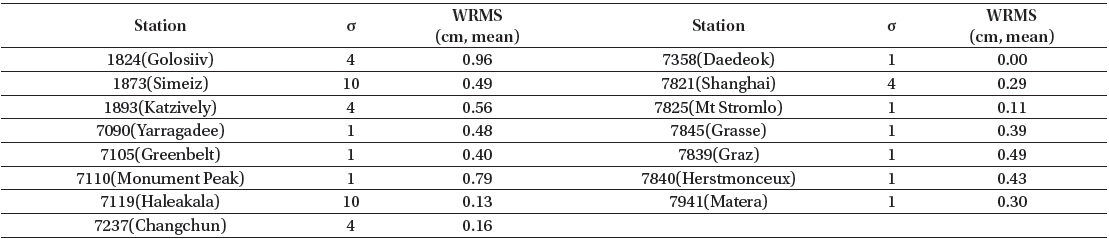
Measurement residuals of each station.
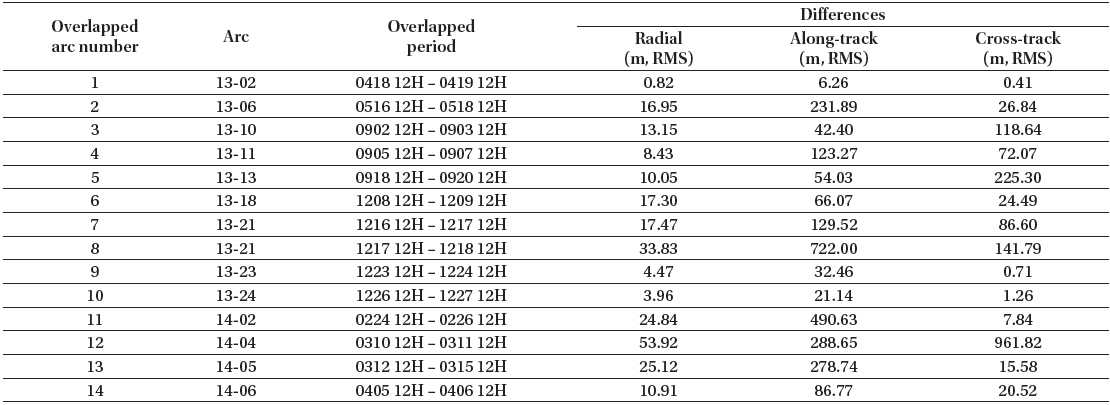
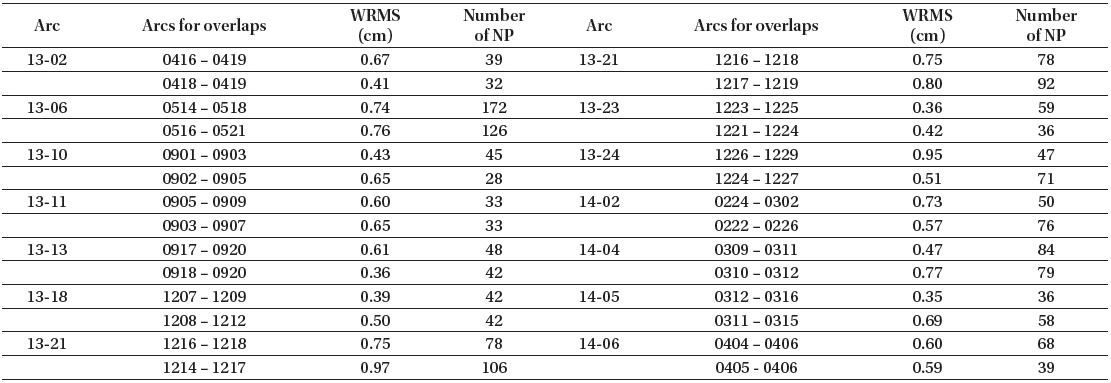
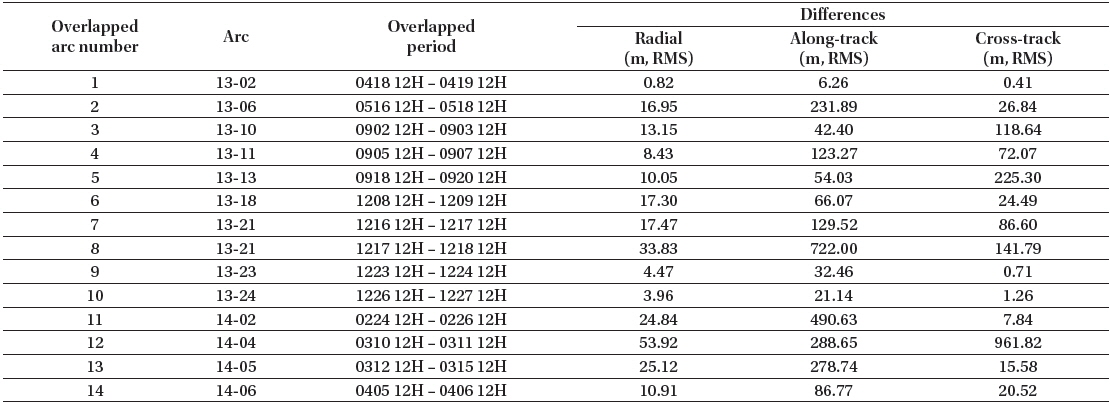
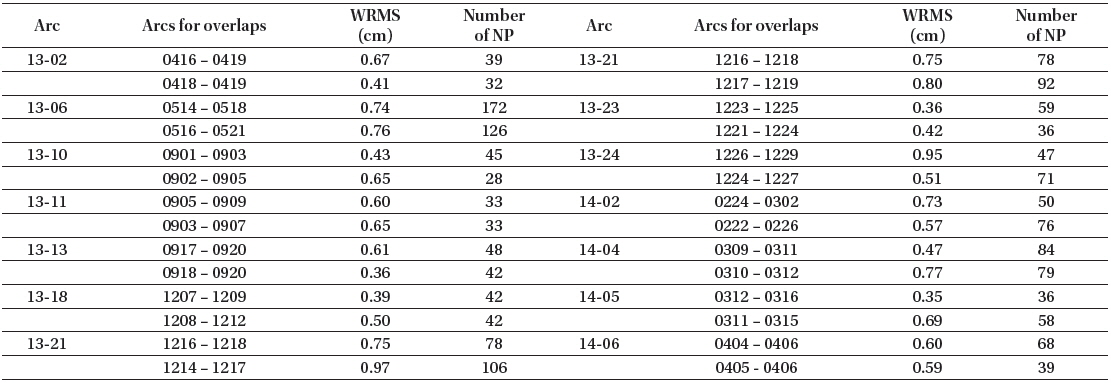
Although the overlapped periods are generally arranged consecutively, we could not find continuous overlapping periods among the sparse arcs for STSAT-2C. Therefore, we extracted a few discrete overlapped periods using several arcs as shown in Tables 6 and 7. For the orbit overlaps, one arc is selected among the previously determined arcs presented in Table 4. The other arc is newly determined using a day close to the first arc. To include more periods, the two orbit overlap concept displayed in Fig. 6 is utilized in the section. In the first case, the new arc is included in the previous arc, and in the second case, the two arcs have a common period in the middle of the arcs. The details of the arcs’ orbit overlaps and their post-fit residuals are presented in Table 6. The post-fit residuals (RMS) for all arcs’ overlaps are maintained at less than 1 cm.
[Table 6.] Arcs for orbit overlaps of STSAT-2C orbit determination (2013-2014).
Arcs for orbit overlaps of STSAT-2C orbit determination (2013-2014).
[Table 7.] Orbit overlaps results of STSAT-2C orbit determination (2013-2014).
Orbit overlaps results of STSAT-2C orbit determination (2013-2014).
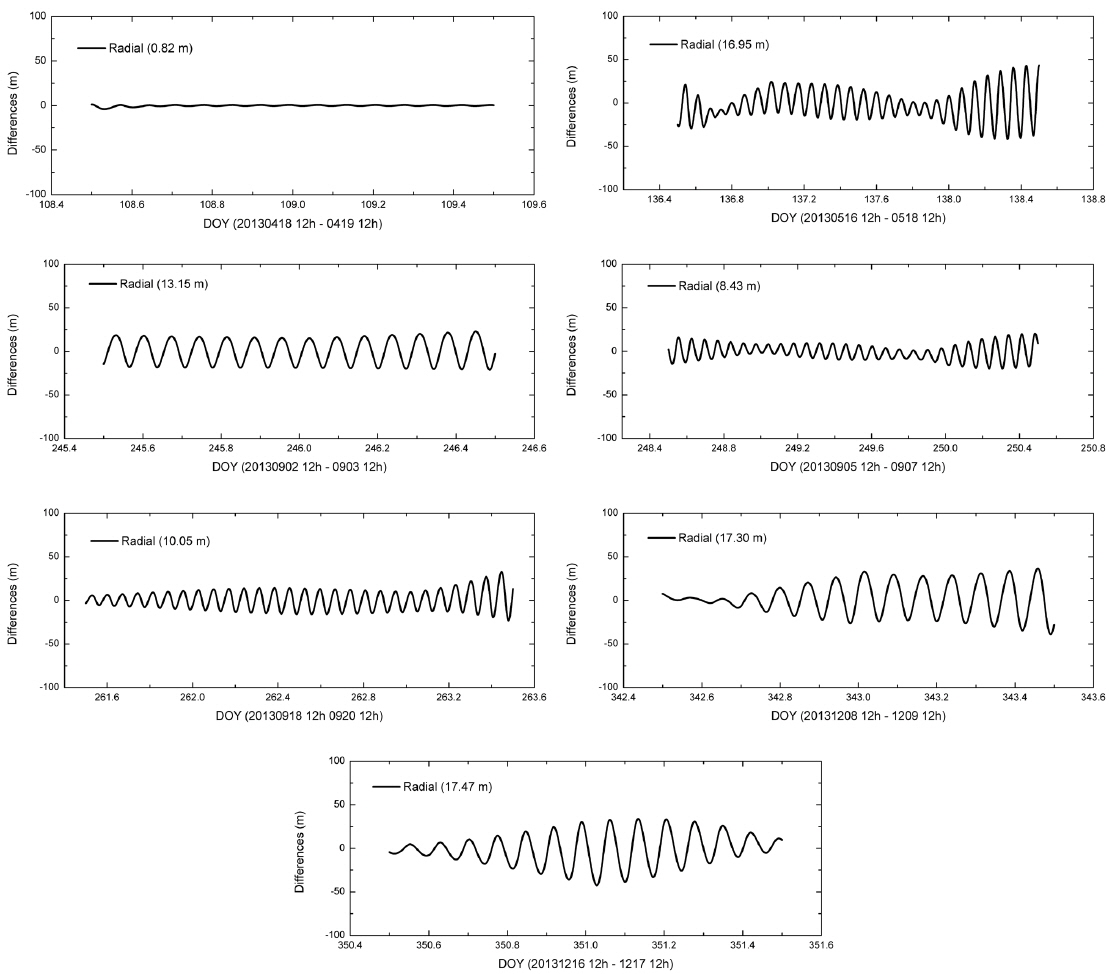
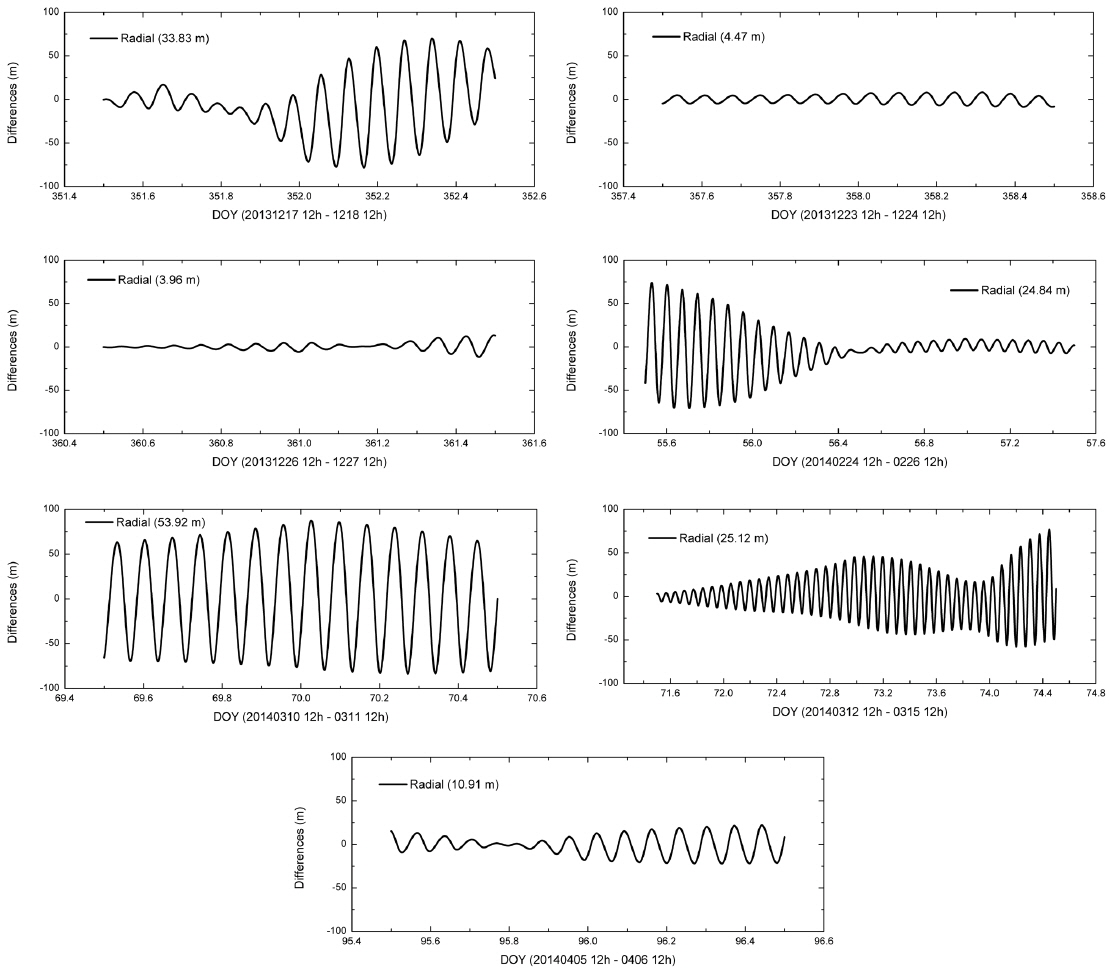
Table 7 shows the overlapped periods and their overlap results for STSAT-2C OD. The first and the last 12 hours of the overlapped periods are eliminated and each period is selected to have a minimum of one day’s overlap. The differences in the overlapped orbits are displayed with the radial, along-track, and cross-track directions. The orbit overlaps results show values varying from 1 m to 1 km. While the post-fit residuals show small differences between two overlapped arcs, the orbit overlaps yield larger variations. This inconsistency is one of the drawbacks of SLR-based OD using sparse range observations. This is a result of orbit-fits in the OD process being performed by using only few short arcs. To avoid this situation, continuous and frequent SLR tracking is essential for STSAT-2C. The differences for the radial direction have relatively small values, less than 50 m. The differences for the along-track and cross-track directions are under 600 m and 900 m, respectively. Figs. 7 and 8 show the differences in the overlapped orbits according to the day of the year in the radial direction. Each overlapped period has its own characteristics in each direction without consistent trends. The along-track and cross-track produce widely different values according to the time. Therefore, we can infer that OD for STSAT-2C using SLR data has shortcomings in the robustness of the along-track and cross-track directions. As the unstable conditions for OD of the STSAT-2C lead to inconsistent accuracy of the orbit overlaps, improvement of the sparse measurements is needed to improve the reliability of the orbit analysis.
In this study, orbit determination (OD) for the STSAT-2C satellite using SLR observations was successfully accomplished by a short-arc approach. OD using SLR normal point (NP) observations over one year was performed by the NASA/GSFC GEODYN II software. Variable estimation intervals for the atmospheric drag coefficients and the empirical acceleration parameters and a non-regular daily-based strategy are applied because the inaccuracy of TLE-based predictions for the STSAT-2C leads to very sparse measurement conditions. The prior value of the initial orbit was obtained from the previous TLE-based predictions through an iterative manual tuning. For the orbit quality assessment, the post-fit residuals and orbit overlaps are analyzed. The weighted root mean square values of the post-fit residuals are at a precision level of under 1 cm. The radial precision of the overlaps shows 50 m accuracy. The precision of the along-track and cross-track directions is less than 600 m and 900 m, respectively. Although the post-fit residuals of STSAT-2C OD have a cm-level precision, the orbit overlap results imply that the 3D orbit accuracy is at the m-level or km-level. This indicates that the lack of SLR observations in STSAT-2C leads to the large difference between OD precision and accuracy. To overcome this inconsistency due to sparse measurement conditions, more SLR measurements through improved orbit predictions are urgently needed. In this sense, the OD for STSAT-2C based on the SLR data is a significant step towards better precision of the orbit prediction. The study of STSAT-2C orbits under sufficient SLR observations would validate the dynamic and measurement modeling accuracy in 300-1,500 km environments.