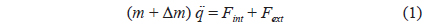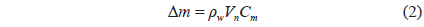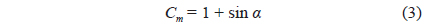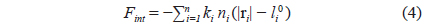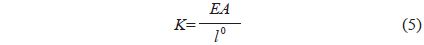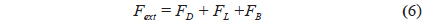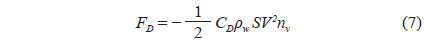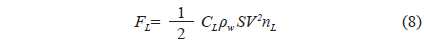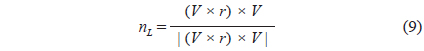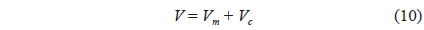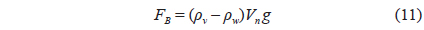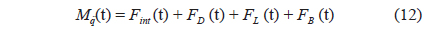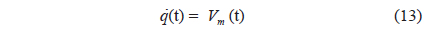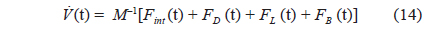Small pelagic fisheries play an important role in Indonesian fisheries and are an alternative to meet the protein needs of the dense Indonesian population. They are also promising employment and a source of income for people living along the Indonesian coast (Dahuri, 2001). Fish caught by purse seine nets in Indonesian waters include scad (Decapterus Sp), black pomfred (Formio niger), Bali sardinella (Sardinella lemuru), trevallies (Selaroides Spp), common squid (Loligo spp.) narrow-barred Spanish mackerel (Scomberomorus commerson), frigate tuna (Auxis thazard), eastern little tuna (Euthinnus affinis), and skipjack tuna (Katsuwonus pelamis) (MMAF, 2010).

The sinking performance of small-scale purse seine gear is typically low in Indonesia, as its development has occurred traditionally. Gear optimization involves increasing the length and depth of purse seine nets (Wijopriono and Mahiswara, 1995). The results of previous studies in Indonesia show that the mean sinking speed of all purse seine nets is very low (Kumajas et al., 1992) and must be improved to prevent schools of fish from escaping the net during shooting (Fridman, 1973). Nets are typically made of nylon braided knotted 210d/12 and 210d/15 for the bunt, and nylon braided knotted 210d/9 and 210d/6 for the net body (Mulyana, 1981). Mesh size is usually small, particularly on the island of Java, where the mean mesh size is 25.4 mm and the fishermen use knotted nets. Low density nylon, small mesh size netting, and knotted nets may decrease sinking speeds.

Headlines, leadlines and purselines are made of polyethylene, which floats in seawater, so it does not contribute to net sinking speed. Accordingly, we noticed that the sinking performance of gear is not optimum. The purpose of this study was to analyze the current gear by using computer-aided tools, and to modify the gear.

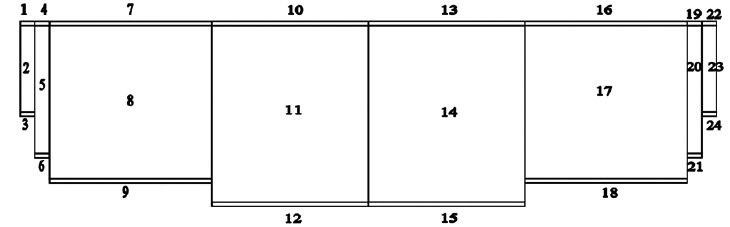
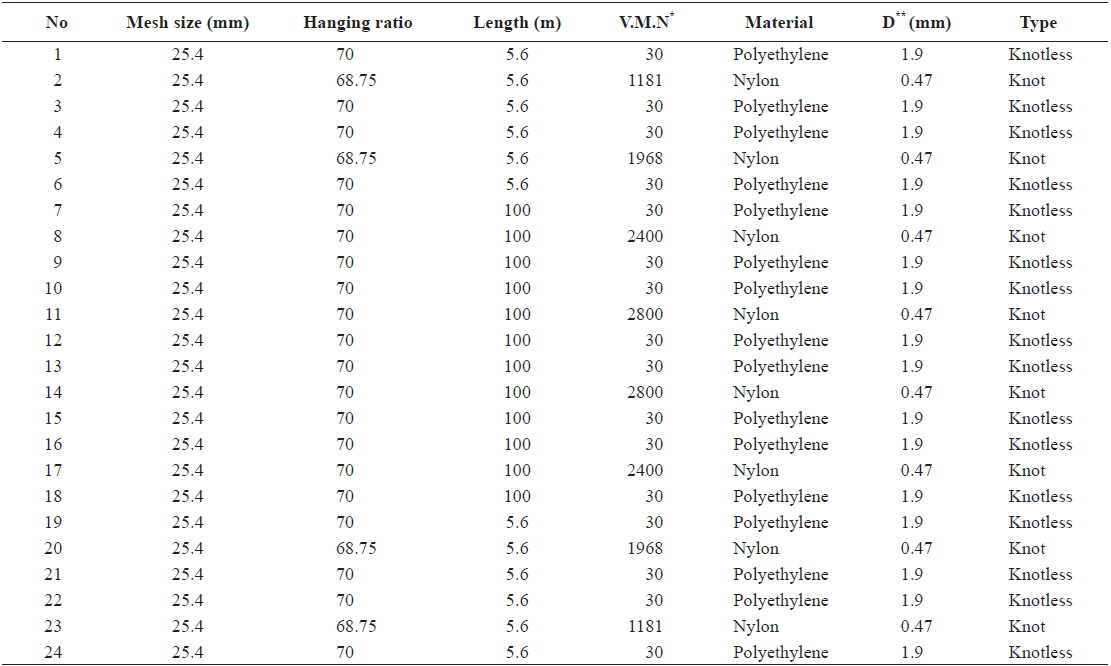
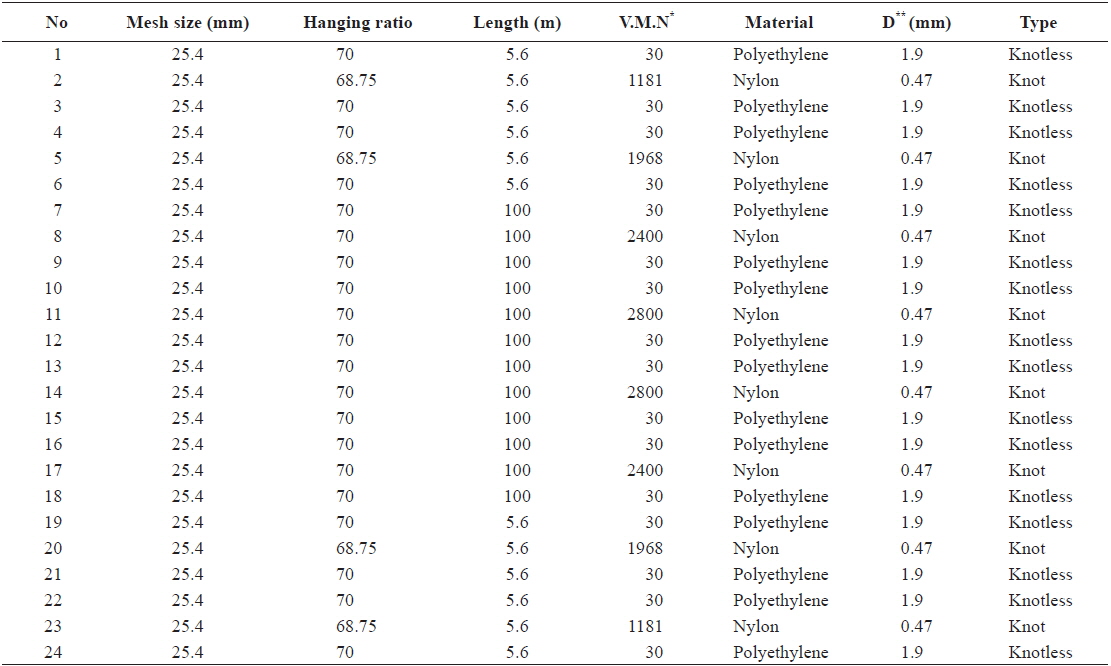
Field trials were conducted to measure the sinking depth of a sinker line during shooting and pursing. Fishing gear sinking depth was measured during one cruise (September 17–September 23, 2013) in a government-owned purse seiner near Karimunjawa Island, Java Sea. We took two measurements at a depth of 35 m. The shooting speed of the vessel was about 6 knots, and shooting time was about 2.40 min. Pursing time was 2.82 min. Measurements were carried out at the middle position of the leadline using a Simrad PI32 depth recorder (Lynnwood, WA, USA). We assessed sea conditions with a current meter (Recording Current Meter CRM 7).Current speeds at the time of measurement were 0.21, 0.18, and 0.21 m/s for the three layers (5, 15, and 25 m), and the current directions were 117, 140, and 131°. The Javan small-scale purse seine gear had a stretched mesh length of 422.4 m, a float line of 295.4 m, a breast line of 30 m, total buoyancy of 793 kg, and a total sinking force of 479 kg/w (Fig. 1). The gear specifications are shown in Table 1.

We observed net sinking using four nylon nets with the same twine thickness of 0.47 mm, the same length and depth (1 × 1.5 m), and the same hanging ratio (75%). These nets had mesh sizes of 25.4, 30.8, 50.8, and 75 mm, and different total sinking forces of 18.24, 27.36, and 45.6 g/w. An underwater camera (Nikon D90, housing/strobe/light dr Sealux; Tokyo, Japan) and a vertical ruler (wooden ruler, 100 cm) were used during the experiment.

We observed net sinking depths using different mesh sizes and different total sinking forces in a swimming pool (25 × 15 × 1 m). The nets were deployed on the water surface of the swimming pool and left free to reach the bottom. Each net was released in the water in front of the vertical ruler.

Factors that must be considered to improve purse seine sinking speed in water are the weight of the net in water, knot type, mesh size, twine thickness, hanging ratio, mesh geometry, and floatline length. The gear must have low water resistance.

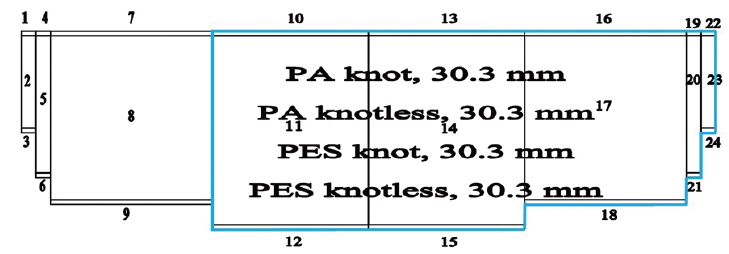
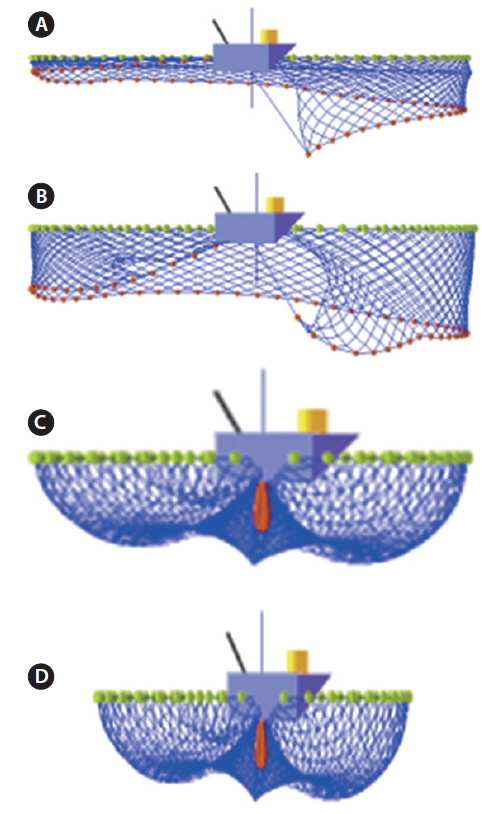
The analysis showed that the polyester purse seine net had the fastest sinking speed, followed by polyamide, and polypropylene. A purse seine net with more sinker weights also sinks faster (Kim, 2004). According to Misund (1992), using a larger mesh in the part of the net near the leadline increases sinking speed. A dynamic simulation verified by a field experiment indicated that larger-mesh polyester tuna purse seine gear without knots had better sinking performance than other gear (Hosseini et al., 2011). In this study, we present gear that was modified by changing the mesh size, net material, and knot type in the net body (Fig. 2).

Equation of motion

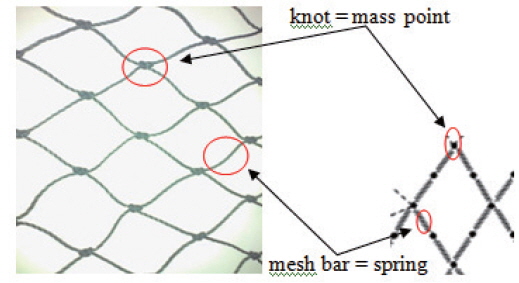
We modeled a purse seine gear system based on the massspring model (Lee et al., 2005). This model can be used to design and simulate the dynamic movement of fishing gear systems, such as a purse seine (Kim et al., 2004; Kim et al., 2007), trawl (Lee and Cha, 2002), long-line (Lee , 2005), or fish cage (Lee et al., 2008). This model was improved by determining the drag coefficient as a function of the attack angle and the Reynold’s number, as mentioned in a previous study (Hosseini et al., 2011). The mesh knots in purse seine netting applied to this model are the mass points and the mesh bars are the springs connecting the mass points (Fig. 3). There are thousands of mass points in purse seine gear. Loads must be reduced by using an approximation method, in which several actual mesh sizes are bundled together into a virtual mathematical mesh with the same physical properties.

The equation of motion for each mass point can be described as mentioned in a previous study (Lee et al., 2005):

where m is the mass of the mass points, dm is the added mass, q̈ is the acceleration vector, F_int is the internal force applied between the mass points, and F_ext is the external force applied to the mass points. The added mass of the mass points is:

where ρ_w is the density of seawater, V_n is the volume of the mass points, and C_m is the added mass coefficient, which is set to 1.5 because the structure is assumed to be a sphere.

C_m is calculated as:

Where α is the angle of attack.

Internal force

The internal force is the force in the springs. The force is assumed to be in the direction of tension when applied to the netting and rope, or in the direction of tension and compression when applied to the floating collar. The internal force can be calculated as follows:

where k_i is the spring stiffness, n_i is the unit vector along the line of the spring, |r_i| is the magnitude of the position vector between the neighboring mass points, is the initial length of the spring, and n is the number of adjacent mass points i.

The stiffness of each material is calculated using the following formula

where E is Young’s modulus and A is the effective area of the material. The effective area of the rope, mesh bar, or wire is 60% of the apparent cross-sectional area, and the effective modulus of the mesh bar or rope is assumed to be 60% of the modulus of the materials (Lee et al., 2008).

External force

The external force is the outside force acting on each mass point in seawater. These forces cover the drag force (F_D), lift force (F_L) and buoyancy, and sinking force (F_B). The equation is as follows:

Current is steady and uniform in the external force equation. The drag and lift forces are calculated as follows:

where C_D is the drag force coefficient, S is the projected area of the mass point, V is the magnitude of the resulting velocity vector, n_v is the unit vector of the velocity vector, C_L is the lift force coefficient, and n_L is the direction of the lift force.

n_L is calculated as follows:

where V is the resulting velocity vector. V is the motion velocity vector of the mass point V_m and the current velocity vector V_c.

This equation does not determine the influence of the mutual interference of the velocity field.

Buoyancy and sinking force, F_B, are calculated as follows:

where ρ₁ is the density of the structure, and g is the gravity of acceleration.

Computational method

The internal and external forces must be substituted in Eq. (1), and the equation of motion governing the motion of the purse seine system becomes the following non-linear second-order derived differential equation in the time domain:

where M is total mass, and is q̈(t) acceleration. This equation can be made into two first-order differential equations:

We integrated the equation using the fourth-order Runge-Kutta method to solve the behavior of the structure.

Fishing gear simulation software that adopts the mass-spring model was used in this study. The field data for the small-scale purse seine gear was used to draw the design of Javan small-scale purse seine gear before the simulation. Once the design was made, preparations for the simulation were completed by selecting the approximation ratio to make virtual mathematical mesh automatically as a mesh grouping process. Then, the real data from the field experiment at sea, such as shooting speed (6 knots), pursing speed (1.4 m/s), sea depth (35 m), ship property, current speed for the three layers (0.21, 0.18, and 0.21 m/s), and current direction for the three layers (117, 140, and 131°) were inputted before running the simulation.

We calculated the following in this simulation: Sinking performance of Javan small-scale purse seine gear. Sinking performance of the improved gear.

Field experiment results

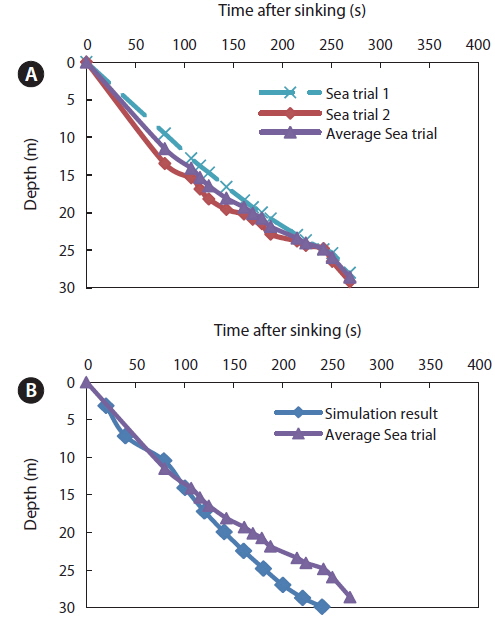
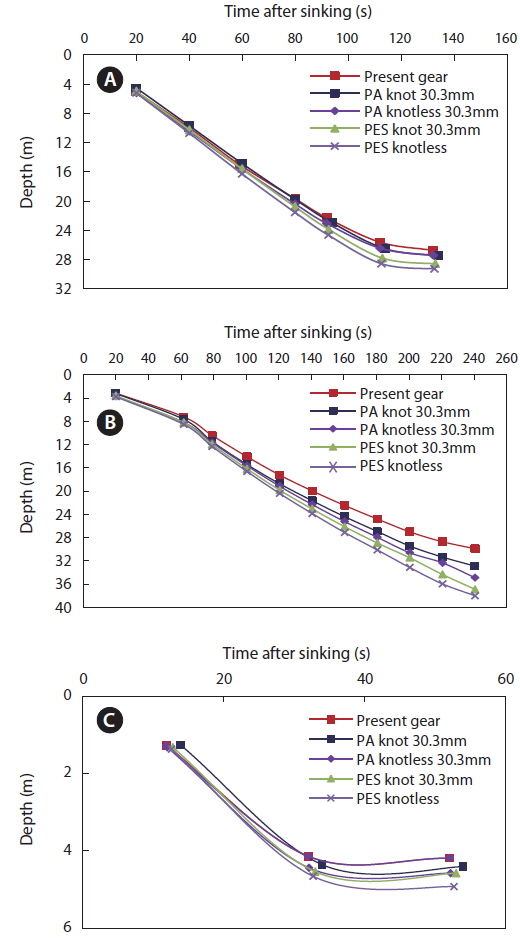
The field experiment measured the sinking depth of the sinker line during shooting and pursing (Fig. 4a). Measurements were taken in the middle position of the leadline because this area sinks freely without being affected by factors that affect measurement accuracy. For example, when the sinking speed is measured at the first leadline position, the net can be affected by the skiff maintaining its position (Hosseini et al., 2011).

In this study, the depth reached by the middle position of the leadline (30 m) was similar to that of the calculated result (Fig 4b). The results of an independent sample t-test showed that the mean sinking depths in the simulation and measurement results were not significantly different (two-tailed P = 0.575. Mean sinking speeds also did not significantly differ between the simulation and measurement results (two-tailed P = 0.197. The mean speed values from the simulation and measurement results did not significantly differ (P > 0.05).

In a previous study using tuna purse-seine gear, the sinking speed of a purse seine net during operation was slightly different from the calculation (Hosseini et al., 2011), which may have been caused by ship maneuvers, the effect of the net being pulled by the winch, or pursing speed. Also, nets often tangle with the floatline, sinker line, or purse ring when shot. The simulated shooting did not result in tangling.

The improved numerical model used in this study can represent the effect of drag force on the net wall. Of course, the results of this numerical method will not be as accurate as a field measurement, as it is so difficult to enter data about the actual conditions of the operation for a simulation. However, the difference becomes smaller after calculating the drag coefficient on the net wall, considering the Reynold’s number and an accurate attack angle value.

Net sinking results

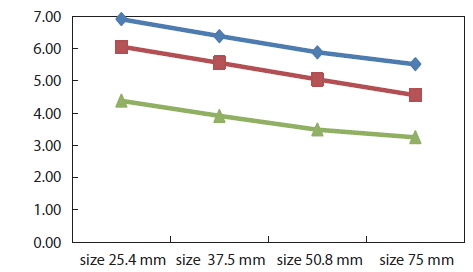
Net with large mesh size sank faster than net with small mesh Fig 5. Adding sinking force with a leadline increased net sinking speed. The sinking speed of various model nets with different mesh sizes showed that the time required to reach 1 m depth for a model net with a mesh size of 25.4 mm and with a total sinking force of 18.24 g/w was 6.92 s, whereas 5.52 s was required for a net with a mesh size of 75 mm. Similarly, 6.06 s was required to reach a 1 m depth by a net with a total sinking force of 27.36 g/w and a mesh size of 25.4 mm. A total of 4.56 s was required for a net with a mesh size of 75 mm. Finally, 4.38 sec was required for a model net with a total sinking force of 45.6 g/w and a mesh size of 25.4 mm to reach 1 m depth, whereas a net with a mesh size of 75 mm took 3.25 s. Some studies have shown that larger mesh increase nets’ sinking speed (Misund et al., 1992; Hosseini et al., 2011). Increased sinking speed is important to reduce the number of fish that pass under the leadline. It is recommended that the net confine fish as soon as possible by shaping the bag to close the gap immediately, so that fish cannot escape.

Comparison of the simulated sinking performance of current and modified gear

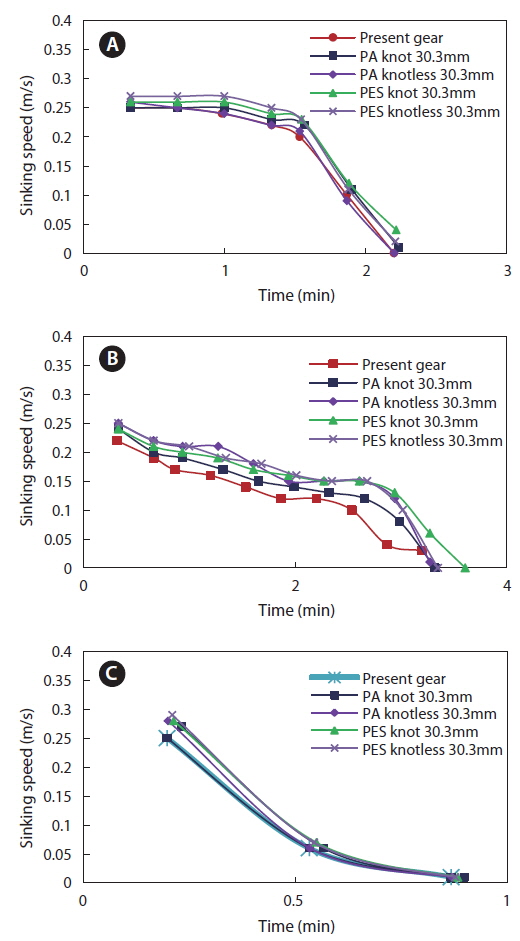
Fig. 6 illustrates the shape of the simulated gear during shooting and pursing. According to Figs. 7 and 8, the sinking performance of the modified gear was better than that of the current gear. The best sinking performance found was for modified gear that used knotless polyester net with a mesh size of 30.3 mm in the body of the net. Comparing the modified gear (PES knotless, 30.3 mm) to the current gear, at the first leadline position the maximum depth reached by the net increased from 26.7 to 29.8 m and the mean sinking speed increased from 0.18 to 0.2 m/s; in the middle position, the maximum depth reached increased from 29 to 38 m and the mean sinking speed increased from 0.13 to 0.16 m/s; and in the end position, the maximum depth increased from 4.2 to 5 m and the mean sinking speed increased from 0.1 to 0.12 m/s. This is consistent with the results of Hosseini’s research, in which the sinking rate increased with increasing mesh size and the specific gravity of the material.

Tension at both ends of the purse line during pursing

The purse line tension calculation is important because it determines the machinery and hydraulic power necessary for pursing and net hauling. Based on the simulation results, increasing the net mesh size would decrease pursing tension. Using the current gear with a mesh size of 25.4 mm, the maximum tension reached was 1,794 kgf. Lower tension was exerted by the new gear with a mesh size of 30.3 mm. Tensile forces were lowest using a knotless polyester net with a mesh size of 30.3 mm, for which the maximum tension was 1,044 kgf. These results indicate that current vessel facilities could be used, even if the fishing gear is improved as proposed in this study.

The change to a larger mesh size and the change in material from nylon to polyester increases net sinking speed and reduces tension at both ends of the purse line. Net sinking speed can be increased and the net can be made more friendly to the environment.

Our investigation of the sinking performance of purse seine nets composed of different materials and knot types indicated that knotless polyester net has the best sinking performance. We compared the simulated sinking performance of current and modified gear (PES knotless, 30.3 mm) in the first leadline position. As a result, the maximum depth reached by the net increased from 26.7 to 29.3 m and the mean sinking speed increased from 0.18 to 0.2 m/s. In the middle position, the maximum depth increased from 29 to 38 m and the mean sinking speed increased from 0.13 to 0.16 m/s. In the end position, the maximum depth increased from 4.2 to 5 m and the mean sinking speed increased from 0.1 to 0.12 m/s. We used various design options to improve the sinking performance of the traditional Indonesian gear. Therefore, these results will be helpful in choosing design parameters to improve purse seine gear.