컨테이너선의 전손 사고 (MAIB, 2008; NK, 2014)로 인하여, 최종 종강도 능력(capacity)에 대한 검증 필요성이 증대되고 있다. 또한, 선체 크기가 점점 대형화 됨에 따라 휘핑에 의한 종굽힘 하중이 추가되는 상황 임에도 컨네이너선의 최종 종강도 요건에 강제 규정이 현재까지 선급규칙에 반영되지 못하고 있는 실정이다. 이에 따라, 현재 국제선급연합회(IACS)는 산적화물선과 탱커선에 적용하던 공통구조규칙 (IACS, 2014)의 최종 종강도 요건을 컨테이너선에도 적용하기 위하여 통일규칙 (IACS, 2010)을 개정 중에 있다. 본 연구는 CSR의 최종 종강도 계산에 사용되는 간이해석법을 사용하여 두 척의 크기가 다른 컨테이너선의 최종 종강도를 계산하고 이를 비선형 유한요소해석 결과와 비교하여 CSR의 간이해석법의 적용 가능성을 검증하고, 화물하중 및 수압과 같은 면외 하중(out of plane load)에 따른 이중저 굽힘으로 인한 최종 종강도 감소량을 계산하여 이에 대한 안전계수를 제시하고자 하였다.
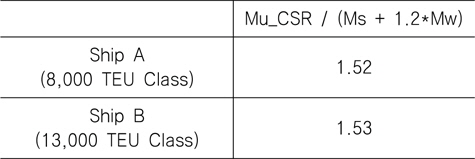
먼저, IACS의 CSR의 간이계산법을 사용하여 컨테이너선의 최종 종강도를 계산한 결과를 Table 1에 나타내었다. 계산된 최종 종강도는 호깅(hogging) 조건에서 M (M = Ms + 1.2*Mw, 여기서 Ms: 정수 중 굽힘 모멘트, Mw: 파랑 중 수직 굽힘 모멘트, 1.2: 신뢰성 해석을 통하여 결정된 Mw에 대한 부분 안전계수, CSR Part 1, Chap 5, Sec. 2.2 참조)의 150% 정도로 설계 종강도와 비교하여 충분한 최종 종강도를 보유하고 있음을 알 수 있다. 그러나, CSR의 간이계산법은 화물 하중 및 수압 등의 면외 하중에 의한 이중저 구조의 굽힘을 반영하지 못하고 있다. 따라서, 이러한 면외 하중이 포함된 실제 운항조건을 고려할 경우 최종 종강도는 감소될 것이다.
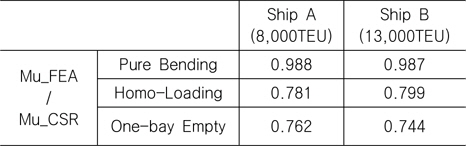
[Table 1] Ultimate hull girder strength (hogging) for Container ship
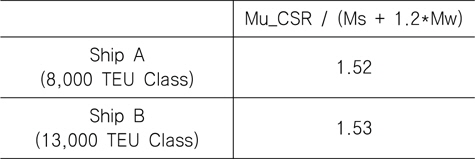
Ultimate hull girder strength (hogging) for Container ship
CSR의 간이계산법은 Smith 법(Smith’s method)로 알려진 방법으로 선체횡단면을 구성하는 모든 구조부재를 보강판(one-bay stiffened panel) 단위로 분리한 뒤, 각 보강판 요소의 인장/압축에 따른 응력-변형율 선도를 기반으로 최종 종강도를 계산하는 방법이다. 따라서, 보강판 요소의 응력-변형율 선도를 어떻게 정의 하느냐에 따라 최종 종강도의 정확성이 영향을 받는다. CSR의 간이계산법은 응력-변형율 정의에 있어서 국부적 굽힘을 유발하는 자중, 화물하중, 정수압 및 파랑에 의한 동적 수압 등의 면외 하중이 고려되지 않고 있기 때문에, 실제 하중상태를 반영한 최종 종강도 계산이 불가능하다. 따라서, 이를 보완하기 위하여 CSR에서는 화물창 내 국부적 굽힘을 고려한 부분 안전계수(1.1: 균일 적재 조건, 1.25: 격창 적재 조건)를 포함하고 있다.
간이계산법 이외에 최종 종강도를 계산하는 방법은 비선형 유한요소 해석법이 유일하다. 일반적으로 비선형 유한요소해석은 설계단계에서 흔히 사용하는 선형해석과는 달리, 구조부재에 대한 기하학적 비선형 및 재질 비선형을 고려할 수 있기 때문에 좌굴 및 소성변형 등의 영구적 손상을 규명하는데 사용될 수 있다. 따라서, 비선형 유한요소해석은 선체 거더 붕괴 시뮬레이션, 즉 최종 종강도 직접 계산에도 유용한 수단이 된다. 다만, 앞서 언급한 기하학적 대변형 및 변형율 경화(strain hardening)를 표현하기에 충분할 정도로 아주 상세한 요소 분할이 요구되는 점과 하중이나 변위 또는 시간 증분 횟수에 비례하는 반복 계산 과정으로 인하여 해석 시간이 오래 걸리고 고성능 전산 장비가 투입되어야 하므로 많은 비용이 요구된다.
비선형 유한 요소 해석법은 하중 증분 단계 마다 강성 행렬의 역행렬을 계산하여야 하는 내연적 방법(implicit method)과 질량 행렬의 역행렬을 최초 한번만 계산하는 외연적 방법(explicit method)으로 구분된다. 내연적 방법은 시간에 따라 급격하게 변하지 않는 정적(static) 또는 준정적(quasi-static) 하중인 경우에 사용되며, 외연적 방법은 아주 짧은 시간 동안 하중이 급격하게 변하는 충돌과 같은 문제에 사용된다.
따라서, 항해 중 선박에 작용하는 종굽힘 하중과 같은 정적 또는 준정적 문제에는 내연적 방법을 사용하여야 한다. 본 연구에서도 내연적 방법 기반의 상용 프로그램(NASTRAN, ANSYS 등)을 사용하여 해석을 시도하였으나, 상세 분할되어 100만개에 근접한 요소 수를 갖는 대형 유한요소 모델에서는 계획된 하중 단계까지 해석이 진행되지 못하고 해석 도중에 발산되었으며 모델 수정, 증분 방법 및 증분량을 조절하여도 발산되는 문제를 해결하지 못하였다. 이와 같은 원인으로는 프로그램의 계산 알고리즘의 문제로 추측된다. 따라서, 본 연구에서는 일반적으로 해석의 정확도는 약간 낮으나(감차적분 요소 적용 등에 기인 되어) 해석 도중 발산되지 않는다고 알려진 외연적 방법 (LS-DYNA Explicit, LSTC, 2006)을 사용하여 비선형 유한요소 해석을 수행하였으며 그 결과를 CSR의 간이계산법 결과와 비교, 검토하였다.
선체 최종 종강도 계산과 관련된 기존 연구로는 산적화물선과 탱커선의 최종 종강도 간이해석법 연구 (Cho, et al., 2004; Choung, et al., 2013) 등이 있으며, 본 연구와 유사한 연구로는 산적화물선에 대하여 비선형 유한요소해석을 사용하여 최종 종강도를 계산한 연구 (Dariel, et al., 2013)와 컨테이너선을 대상으로 비선형 유한요소해석을 수행한 보고서 (NK, 2014)가 있다. 본 연구에서는 이러한 연구 결과 및 해석 절차들을 참조하여 수행하였다.
2.1 유한 요소 모델(Finite element model)
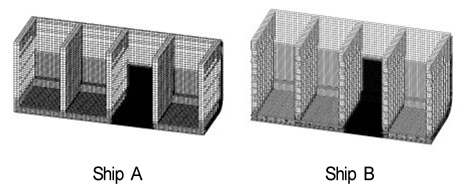
Table 1에 보인 바와 같이 크기가 다른 2척의 컨테이너선을 대상으로 유한요소 모델의 범위는 Fig.1과 같이, 선박의 중앙부에 위치한 3개 화물창(1/2+1+1/2)이며, 대칭을 고려하여 선체의 반폭만을 모델링 하였다. 선체 거더 최종 종강도를 계산할 때, 면외 하중을 고려하지 않을 경우에는 선체 길이 방향으로 특설 늑골 간격의 종부재 만을 모델링 하여도 되나, 격창 적재 조건과 같은 실제 하중 상태를 고려하기 위하여, 본 연구에서는 선체 길이 방향으로 2개의 화물창 길이를 갖는 모델을 사용하였다. 사용된 요소는 탄소성 해석에 적합하도록 Solver(LS-DYNA Explicit) 에서 권장하는 4절점 Shell요소와 2절점 Beam 요소를 사용하였다.
일반적으로 컨테이너선은 운항 중인 상태가 거의 호깅(hogging) 상태이므로 압축에 의한 좌굴과 이에 따른 소성 변형이 선저판 부터 시작될 것이므로 상세 분할 구간은 기존 전손 사고의 손상 부위를 참조하여 좌굴 붕괴가 예상되는 중앙 화물창의 지지 격벽(support BHD)의 전방 길이 방향으로 3개의 늑판 간격으로 하였으며, 깊이 방향으로는 중립 축에서 선저판까지 이다. 상세 분할 구간의 요소크기는 50 ~100 mm 이며 그 외 상세분할 구간이 아닌 곳의 요소 크기는 화물창 구조해석에서 보편적으로 사용하는 보강재와 보강재 사이 간격으로 하였다. 전체 자유도(degree of freedom)는 2개의 컨테이너선 모두 180만개(요소 수는 대략 100만개 정도) 이상 이었다.
2.2 초기 결함(Initial imperfection)
선체는 건조 시 용접 작업 등으로 인하여 초기 결함을 가지게 되는데 이러한 초기 결함의 크기는 IACS의 권고안 47 (IACS, 2013) 에서 제시한 최소 허용공차를 만족하도록 명시되어 있다. 본 연구에서는 선박의 실제 기하학적 상태를 반영하기 위하여, 유한 요소 모델에 건조 공차에 의한 초기결함을 반영하였다. (실제 완전한 모델에 대하여 압축 하중을 가할 경우 좌굴과 같은 기하학적 대변형이 발생되지 않는 경우가 있기 때문에, 초기 결함을 반영 함으로서 기하학적 대변형을 유발 시킬 수 있음).
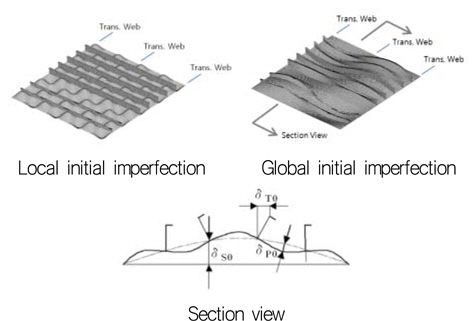
선체 구조부재의 초기 결함은 국부 결함(local defect)과 전체 결함(global defect)으로 분류하여 중첩하여 고려되어야 한다. 국부 결함은 보강재와 보강재 사이의 판에 대한 초기 결함을 의미하고 전체 결함은 거더 및 특설늑골을 경계로 하는 보강판(multi-bay stiffened panel)의 초기 결함을 의미한다. 일반적으로 이러한 초기 결함들은 사인(sin) 함수를 이용한 반파(half-wave)로 표현되는데, 중요한 점은 보강판 전체에 대하여 결함을 생성 시킬 때, 보강재 자체의 트리핑(tripping)도 고려하여야 한다는 것이다. 본 연구에서는 간단한 프로그램을 작성하여 초기 결함을 생성하였으며, 앞서 언급한 Rec. 47에 따라 Fig. 2와 같이 국부 결함의 최대크기는 δP0 = s/200 (s = 보강재 간격, Stiffener spacing), 전체 결함의 최대크기는 δS0 = δT0 = l/1000(l = 보강재 길이, Stiffener span) 을 사용하였다. 국부 결함과 전체 결함은 중첩되어 유한 요소 모델의 초기 결함으로 반영되었으며, 초기 결함이 적용된 구조 부재는 선저판, 내저판, 선측판 및 종격벽과 이 부재들에 부착된 보강재이고 상세 분할 구간 내로 제한하였다.
초기 응력이라 함은 건조 시 용접에 의하여 발생되어 구조부재에 잔류하는 응력으로, 이러한 초기 응력으로 인하여 최종 강도가 구조 부재 별로 2~15% 정도 감소되는 것으로 알려져 있다(Gannon, et al, 2012). 본 연구에서는 사용된 유한요소 모델이 상당히 복잡하고 대형 모델이기 때문에 상세 분할 구간에 있는 모든 요소에 용접 잔류 응력에 해당하는 초기 응력을 전부 입력하여 해석하는 것은 현실적으로 곤란하였다. 따라서 초기 응력에 의한 최종 종강도 감소는 고려하지 않았으며 본 연구 이후 향후 과제로 수행하고자 하였다 (CSR에서는 초기 응력 또는 불확실한 요인으로 인한 최종 강도 감소에 대한 안전 계수로 1.1이 추가로 적용되고 있음).
2.4 재료 비선형(Material nonlinearity)
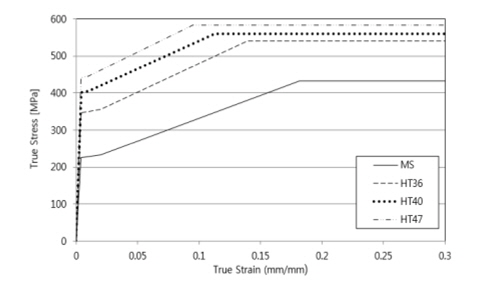
강재(steel)와 같은 재료의 탄-소성 거동은 진응력-진변형율 (True stress – True strain)으로 표현되는데, 본 해석에서는 Fig. 3에 나타낸 바와 같이 유럽 표준 (European Standards EN-10025, 2004; EN-10225, 2012)을 참조하여, 탄성(elasticity) 영역, 소성경화(hardening) 영역 및 완전 소성(perfect plasticity) 영역으로 나눠진 구분적 선형(piecewise linear)을 반영하였다.
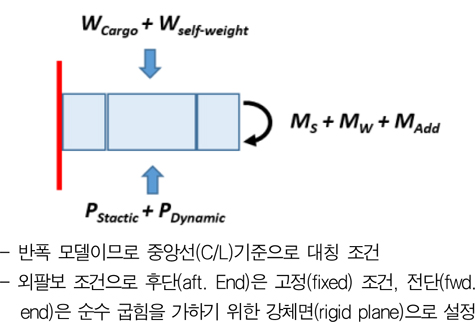
선체 거더의 종굽힘을 해석하기 위한 경계 조건은 선체 길이 방향으로 양단 단순지지 또는 선체 후방 끝단을 고정하고 전방 끝단은 자유단으로 설정하는 외팔보(cantilever system) 조건을 적용할 수 있다. 본 연구에서는 Fig. 4와 같은 경계조건을 적용하였다.
운항 중인 선박은 적하지침서(loading manual)에 명시된 바와 같이 선체 길이 방향으로 각 단면마다 단면 하중(sectional load, 굽힘 모멘트 및 전단력)의 크기가 다르다. 따라서, 2~3개의 화물창 길이로 제한된 화물창 유한 요소 모델에 대하여 하중 평형을 유치한 채 실제 단면 하중 분포를 구현하여 구조 해석 하는 것은 상당히 복잡한 절차가 요구된다(CSR의 직접 구조해석 절차 참조).본 연구의 목적은 선체 거더의 최종 종강도 계산이므로, 성긴(coarse) 분할 구역과 상세(fine) 분할 구역으로 결합된 유한요소 모델 전체에 대하여 정확한 하중평형 상태를 구현할 필요는 없다. 따라서, 선체 길이 방향의 각 단면에 동일한 크기의 굽힘 모멘트가 작용하는 순수 굽힘으로 가정하였다.
2개의 화물창 길이에 해당하는 모델 크기 및 외팔보 경계조건에 대하여 면외 하중(화물하중, 선체 자중, 정수압 및 파랑에 의한 동적 수압)이 작용하게 되면, 부가적인 선체 거더 굽힘 모멘트가 발생하게 된다. 그러나 이러한 부가적인 굽힘 모멘트(최종 종강도 대비 3.5% 이내)는 실제 운항 상태와 동일한 호깅 상태이기 때문에 이 상태에서 호깅 순수 굽힘을 증가시켜 최종 종강도를 산정하면 된다.
본 연구의 하중조건은 순수 굽힘 조건(pure-bending condition), 균일 적재 조건(homo loading condition) 및 격창 적재 조건(one-bay empty condition) 이다. 면외 하중이 없는 순수 굽힘 조건은 CSR의 간이계산법 결과와 비교하여 비선형 유한요소해석의 유효성을 검증하기 위함이며, 균일 적재 조건 및 격창 적재 조건은 운항 중인 컨테이너선을 가정한 하중조건으로 면외 하중으로 인한 이중저 구조의 굽힘을 유도하기 위함이다. 이중저 구조의 굽힘을 최대화 하기 위하여 이중저 내부에 평형수나 연료 등은 하중 조건에서 제외 하였다. 하중 작용 순서는 면외 하중을 먼저 작용시킨 후 선체 종굽힘을 작용시켜도 결과에는 큰 영향이 없을 것으로 판단되나 정적 및 동적 하중으로 분류하여 다음과 같은 순서로 반영하였다.
STEP 1: 선체 자중, 정수압, 컨테이너 하중 STEP 2: 정수 중 굽힘 모멘트(호깅) STEP 3: 파랑에 의한 동적 수압 STEP 4: 파랑 중 굽힘 모멘트(호깅) + 최종 종강도 계산을 위한 추가 굽힘 모멘트(호깅)
외연적 방법을 사용하는 비선형 유한요소 해석은 일반적으로 충돌 또는 충격 문제를 해석하는데 사용된다. 따라서 극히 짧은 시간(0.1초 내외)에 작용 하는 하중으로 인하여 구조 응답은 과도 응답 상태가 된다. 그러나 운항 중인 선박에 작용하는 파랑에 의한 종굽힘 하중은 준정적 하중이며 이에 대한 선체의 응답 또한 정적 또는 준 정적 상태에 해당한다. 즉 전체 하중 작용 시간을 파랑 주기(10초 내외)로 설정 할 경우, 본 연구의 해석 모델과 같이 요소 크기는 매우 작고 요소 수는 아주 대형인 모델의 해석 시간은 내연적 방법을 사용할 때 보다 2~3배 길어지게 된다.
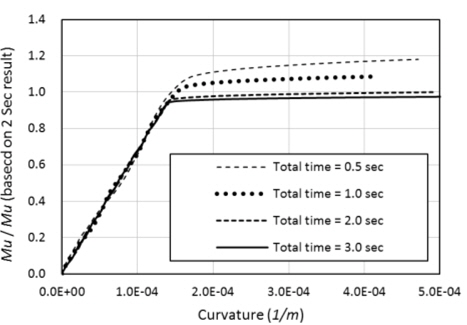
본 연구에서는 해석시간 단축을 위하여 Fig. 5와 같이 종굽힘 하중 작용 시간에 대한 수렴성 조사를 수행하였다. 이 조사를 통하여 상기 하중 적용 순서에 따른 하중 작용 시간은 종굽힘 하중에 대비하여 상대적으로 크기가 작은 하중에 해당하는 면외 하중의 경우 각 1초를 할당 하였으며 종굽힘 하중에 대하여는 3 초를 할당하여 해석을 수행하였다.
3.1 순수 굽힘 조건(Pure-bending condition)
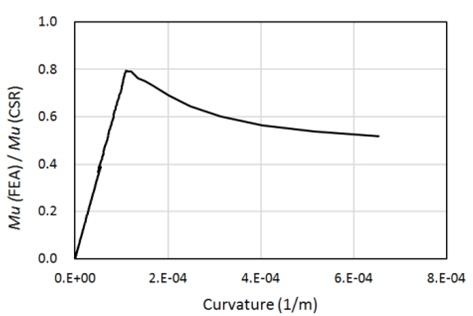
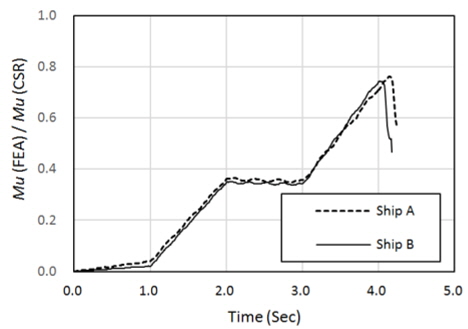
CSR의 간이계산법에 의한 최종 종강도와 비교하기 위하여 순수 굽힘에 대한 비선형 유한요소 해석을 수행하였으며 초기 결함 유무에 대한 영향도 비교, 검토 하였다. Fig. 6에 Ship A(Fig 1. 참조)에 대한 해석 결과를 모멘트-곡률(moment-curvature) 곡선으로 나타내었다. 굽힘 모멘트는 시간 증분 값에 비례하는 값(작용하중 기준)이며 선체 단면의 곡률(curvature)은 화물창 모델 전단의 강체면의 곡률을 의미한다. CSR에 의한 최종 종강도를 기준치(1.0)로 하여, 유한 요소 해석이 완료(발산)된 시점을 최종 종강도로 가정할 경우, 초기 결함이 없는 경우에 대한 해석 결과는 1.058 이었으며 초기 결함이 있는 경우에는 1.024 이었다. 따라서, IACS Rec. 47에서 제시한 최소 건조 공차에 해당하는 초기결함의 영향은 최종 종강도를 3.4% 감소시키는 것으로 계산되었다.
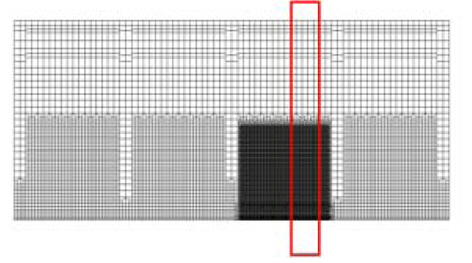
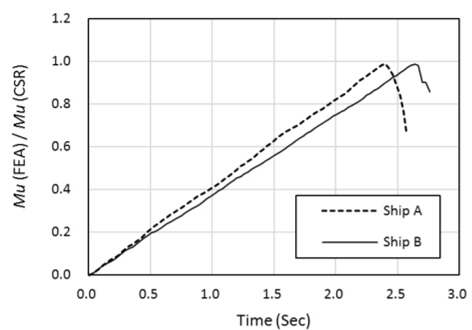
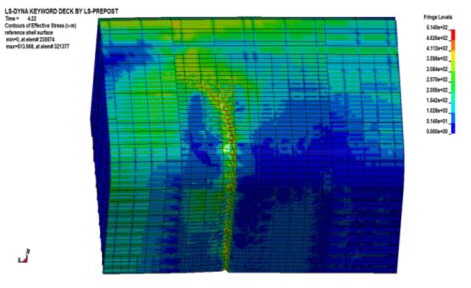
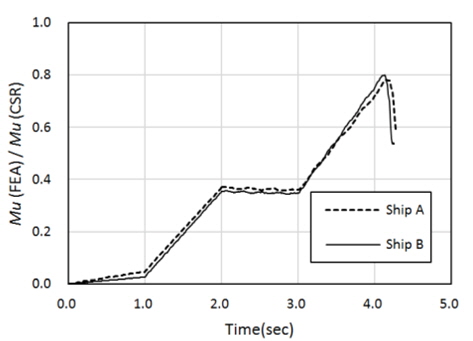
외연적 방법은 내연적 방법의 호장(arc-length) 증분법과 같이 구조물이 최종강도에 근접하여 불안정해질 경우 하중 감분(un-loading)을 수행하지 않기 때문에 해석이 완료되거나 발산할 때까지 하중 증분이 지속되어 모멘트-곡률 선도의 기울기가 영(zero)이 되는 하중 단계가 나타나지 않는다. 따라서, 시간 증분에 비례하는 모멘트 값(작용하중 기준)으로는 정확한 최종 강도를 산정할 수 없다. 따라서 Fig. 7과 같이 붕괴가 발생한 구획의 바로 전방에 위치하는 종부재들의 선체 길이 방향 응력을 취하여 선체 단면에 대하여 적분하여 구한 굽힘 모멘트(구조 응답 기준)를 계산하면 Fig. 8의 모멘트-시간(moment-calculation time) 선도를 통하여 보다 정확히 최종 종강도를 산정할 수 있다.
CSR의 간이계산법에 의한 최종 종강도를 기준으로, 초기결함이 반영된 모델에 대한 순수 굽힘 해석 결과와 비교하면 Ship A의 경우 0.988, Ship B의 경우 0.987로 계산되었다(Table 2 참조). 따라서, CSR의 간이 계산법은 컨테이너선에도 적용 가능할 것으로 판단된다.
[Table 2] Summary of nonlinear FEA

Summary of nonlinear FEA
3.2 균일 적재 조건(Homo-loading condition)
대부분의 컨테이너선의 운항 상태는 균일 적재 조건이며, 컨테이너 하중과 수압 등의 면외 하중이 작용된다. 따라서 화물창을 구분하는 수밀 격벽이나 컨테이너 지지 격벽 사이에 국부적인 굽힘이 발생하게 된다. 이러한 굽힘 거동은 선체 거더 전체에 작용하는 굽힘 모멘트와 결합되어 최종 종강도를 감소시킬 수 있다. 따라서, 본 해석에서는 2.6에 언급한 바와 같이 실제 운항 상태를 반영하기 위하여 이중저 구조의 굽힘을 유발하는 모든 면외하중을 고려하여 계산하였다. Fig. 9와 10에 최종 종강도에 도달하였을 때의 von-Mises 응력 분포 및 변형상태를 나타내었으며, 2.6의 하중 적용 순서에 따른 모멘트-시간 선도를 Fig. 11에 나타내었다. Fig. 12에는 모멘트-곡률 선도를 나타내었다. CSR의 간이계산법에 의한 결과와 비교하였을 때 이중저의 굽힘에 대한 영향으로 인하여 20% 이상 감소하였음을 확인하였다(Table 2 참조). 따라서, 본 연구의 계산 결과에 의하면 면외 하중의 영향은 반드시 고려되어야 하며, CSR의 간이계산법을 최종 종강도 계산에 적용할 경우 균일 적재 조건에 대한 안전계수를 1.2 이상으로 설정해야 함을 알 수 있었다.
3.3 격창 적재 조건(One-bay empty condition)
CSR에서는 격창 적재 조건에서도 면외 하중에 의한 이중저의 굽힘 효과를 고려한 안전 계수를 규정하고 있다. 컨테이너선의 경우에도 Fig. 13 에 나타낸 바와 같이 공창(empty bay) 조건이 있을 경우 컨테이너선 이중저의 굽힘으로 인한 최종 종강도 감소율은 더 크게 증가할 것으로 판단되어 격창 적재 조건에 대하여 비선형 해석을 수행하였다.
참고로 Fig. 13에 나타낸 의 격창 적재 조건은 IACS UR(현재 개정 중)의 컨테이너선의 직접구조해석을 위한 하중 조건 중의 하나이다. 구조응답 기준의 최종 종강도는 Fig. 14에 모멘트-시간 곡선으로 나타내었다. CSR의 간이계산법에 의한 결과와 비교하였을 때 대략 25% 정도 감소하였음을 확인하였다(Table 2 참조). 따라서, 본 연구의 계산 결과에 의하면 격창 적재 조건에 대한 안전계수를 1.25 이상으로 설정해야 함을 알 수 있었다.
컨테이너 선박의 최종 종강도를 계산하기 위하여 비선형 유한요소 해석을 사용하였으며, 그 결과를 CSR의 간이계산법과 비교하였다. 계산 결과는 Table 2에 정리하여 나타내었다. 순수 굽힘 조건에 대한 비선형 유한요소해석 결과는 CSR의 간이계산법과 오차 범위 내에서 동일한 것으로 판단되며, CSR의 간이계산법이 컨테이너선에도 유효함을 확인할 수 있었다. 초기결함에 대한 최종 종강도 감소율은 3.4% 임을 알 수 있었으며, 균일 적재 조건을 고려하였을 때의 비선형해석 결과는 CSR의 결과 대비 80%로 계산되었다. 이 계산 결과에 의하면 CSR의 간이계산법을 컨테이너선의 최종 종강도 계산에 적용할 경우 면외 하중의 영향을 고려하여 안전계수는 최소 1.2 이상으로 설정해야 함을 알 수 있었다. 그러나 본 연구에서는 단지 2척에 대한 결과이므로 보다 다양한 크기의 선박에 대하여 최종 종강도를 계산할 필요가 있다. 향후 과제는 15,000 TEU 이상 다수의 초대형 컨테이너선에 대하여 비선형 유한요소해석을 수행하여 이중저의 굽힘에 대한 안전 계수를 확정할 필요가 있으며 아울러, 현 CSR 간이계산법의 보강판 응력-변형율을 정의하는데 있어서 면외 하중이 포함할 수 있도록 추가 연구가 필요할 것으로 판단 된다.