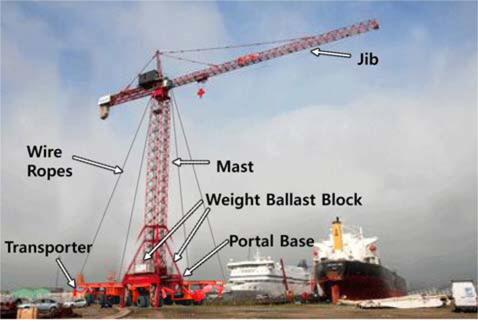
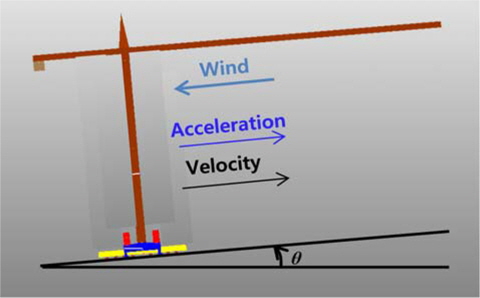
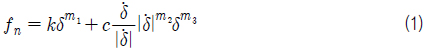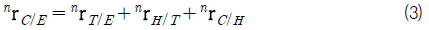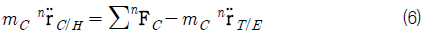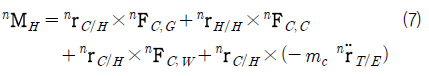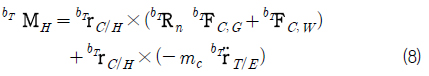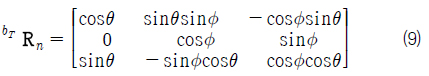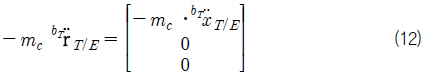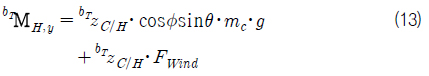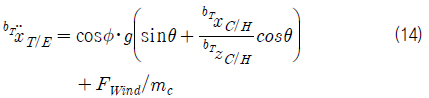조선소 및 건설 현장에서 중량물을 인양할 때 사용되는 타워크레인(tower crane)은 크게 지브(jib), 마스트(mast), 웨이트 발라스트 블록(weight ballast block), 포탈베이스(portal base)로 구성되며, 지브와 마스트의 길이를 조정할 수 있다. 타워크레인의 작업 위치를 변경해야 하는 경우 Fig. 1과 같이 타워크레인을 트랜스포터(transporter)에 올려놓은 후 운송한다.
타워크레인 운송 시 안전을 위해 마스트 높이나 지브의 길이를 조정하는 공법을 적용한다. 따라서 비용과 시간을 절약하기 위해 운송 조건에 따른 타워크레인 거동 안정성을 분석해 적절한 운송 기준을 수립하는 것이 필요하다. 운송 조건으로는 트랜스포터의 출발 및 정지 시 속도, 가속도, 그리고 경사면 기울기 조건 등이 있다. 트랜스포터 및 타워크레인에 작용하는 외력은 풍력 (wind force), 접촉력(contact force), 와이어 로프 장력(wire rope tension) 등이 있다.
본 논문에서는 트랜스포터로 타워크레인 운송 시, 공법 설계자가 타워크레인 거동 안정성 분석 결과를 도출하기에 적합한 모델링 방법을 검토하였다. 모델링 대상은 타워크레인과 트랜스포터 사이의 접촉관계, 평지 및 경사면 위의 이동이다. 검토한 모델링 방법들을 이용해 타워크레인 운송 상황을 시뮬레이션하고, 동역학 계산 결과와 비교하여 모델링 방법의 타당성을 검증하였다.
본 논문의 2장에서는 물체 이동 안정성 분석과 관련된 연구를 살펴본다. 3장에서는 타워크레인 운송 모델링 방법을 설명한다. 4장에서는 검토한 모델링 방법으로 시뮬레이션하고, 5장에서는 시뮬레이션 결과와 동역학 계산 결과를 비교한다. 6장에서 향후 연구계획과 함께 결론을 맺는다.
물체의 이동 안정성 분석을 위해서는 적절한 운송 조건 및이를 고려한 운송 대상의 모델링이 필요하다. Sim, et al. (2013)은 세 바퀴 전기자동차의 무게 중심 이동에 따른 동적 거동 안정성을 분석했다. 세 바퀴 전기자동차의 길이방향 이동 및 횡 방향 회전에 대해 운동 방정식을 구성하고, 정상상태에서의 자동차 무게중심 이동과 횡 동요의 연관관계를 분석했다. 또한 무게중심 이동으로 발생하는 횡 방향 기울기가 자동차 전복에 미치는 영향을 분석했다.
Lee and Rhee (2012)은 주행 면 경사와 무게중심 변동각이 존재하는 차륜형 역진자의 운동방정식을 구성하고, 주행면 경사 및 무게중심 변동각의 영향을 분석하고, 이를 고려해 차륜형 역진자를 정적 평형상태로 유지하기 위한 제어 가능성을 확인하였다.
Cha, et al. (2008)은 병렬 연결된 해상 크레인을 이용하여 대형 중량물을 인양하는 문제에 대해 다물체 동역학 운동방정식을 구성하고, 해상 조건을 고려하여 시뮬레이션을 수행하여 대형 중량물을 인양하는 공법의 안정성을 확인하였다.
본 논문은 대상의 운동방정식을 구성한 것은 다른 연구와 유사하나, 트랜스포터 위에 올려진 상태로 타워크레인을 운송하는 문제에 대해 운송 모델링 방법을 연구하였다. 운송 조건으로는 트랜스포터의 출발 및 정지, 경사면 각도 변화를 고려하였으며, 이 때 타워크레인의 전복과 같은 문제가 없는지 확인하기 위한 동역학 거동 모델링 방법으로 트랜스포터의 접촉면, 평지 및 경사면 이동상황을 검토하였다. 트랜스포터와 타워크레인의 운동 방정식은 다물체 동역학 운동방정식으로 구성하였고, 동역학 계산은 모델링 방법이 적용된 시뮬레이션 결과의 타당성을 검증하기 위해 사용하였다.
타워크레인의 안정성은 트랜스포터 이동 시 타워크레인과 트랜스포터간 상대 기울기 발생 여부, 타워크레인 전복 여부, 와이어 로프의 장력 등으로 판단할 수 있다. 이러한 안정성 판단 결과를 도출하기 위해 타워크레인과 트랜스포터 사이의 접촉면에 대한 모델링 방법과 트랜스포터의 평지 및 경사면 이동 모델링 방법에 대해 검토한다.
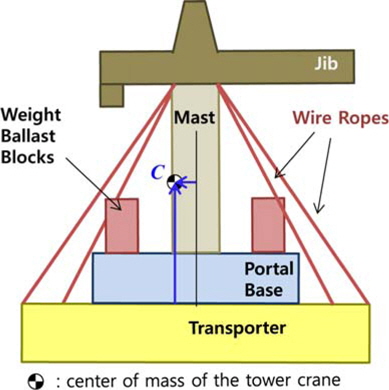
본 논문의 대상이 되는 타워크레인은 지브, 마스트, 포탈베이스, 웨이트 발라스트 블록 2개로 총 6개 부분으로 구성되며, 타워크레인의 총 질량중심은 Fig. 2와 같이 타워크레인 마스트 중심을 기준으로 뒤편에 위치한다.
타워크레인과 트랜스포터 모델링 시 다음과 같이 가정한다.
- 타워크레인을 구성하는 각 부분은 강체로 가정 - 타워크레인 각 부분들은 고정(fixed) 조인트로 구속 - 와이어 로프 4개는 각각 트랜스포터와 마스트 상단에 연결하며 초기 상태에서 장력은 없음 - 트랜스포터의 타이어 및 유압 시스템, 지면의 거칠기, 타워크레인 마스트와 지브의 유연체(flexible) 거동 등은 고려하지 않음 - 정지는 출발과 동일한 현상이므로 출발만 고려
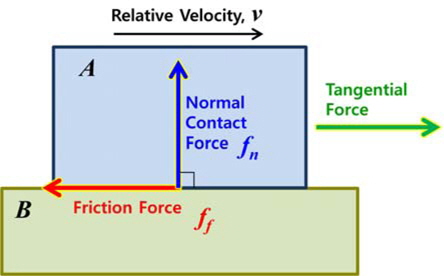
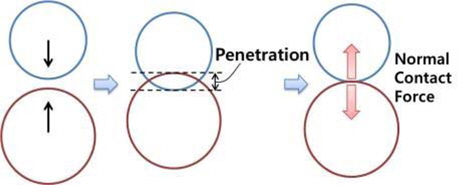
접촉면의 수평방향의 외력(tangential force)을 받아 상대속도 v로 운동을 하는 두 물체의 접촉면에서 작용하는 힘은 Fig. 3과 같이 수직방향으로 작용하는 수직 접촉력(normal contact force)과 수평방향으로 작용하는 마찰력(friction force)으로 분해한다.
접촉력을 수치 해석 기법을 사용해 해석하는 동역학 프로그램들은 보통 수직 접촉력을 두 물체의 간섭 발생 시 침투량(penetration)및 침투 속도의 함수로, 마찰력은 마찰 계수, 상대속도, 수직항력의 함수로 근사하여 표현한다. 식 (1)과 (2)는 수직 접촉력과 마찰력의 계산 예다 (FunctionBay, Inc, 2012).
여기서
수직 접촉력을 계산하는 방법 중 compliant contact force model은 Fig. 4와 같이 두 강체가 접촉할 때 간섭 검사로 침투 량 및 침투 속도를 계산한 후, 이에 대응하는 수직 접촉력을 식 (1)과 같이 계산해 두 물체에 가하는 것으로 구현된다 (Choi, 2009).
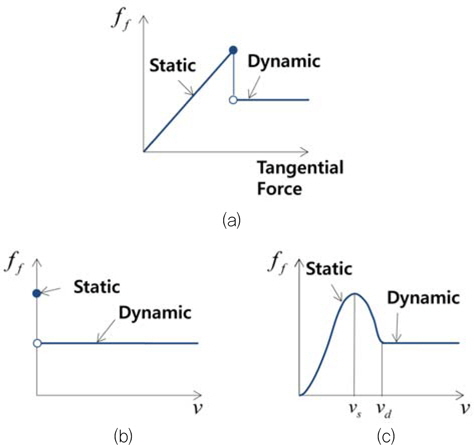
마찰력은 일반적으로 Fig. 5(a)와 같이 쿨롱(coulomb) 마찰력으로 정의한다. 쿨롱 마찰력과 두 물체의 상대속도의 관계를 나타내면 Fig. 5(b)와 같이 정지 마찰력과 운동 마찰력이 작용하는 구간 사이에 불연속점이 존재하는 불연속 함수 형태이다. 실제 동역학 프로그램들에서는 불연속점을 수치 해석 기법으로 계산하기 어려우므로 식 (2) 및 Fig. 5(c)와 같이 연속함수로 근사하여 표현한다.
여기서
식 (2)의 마찰계수
여기서
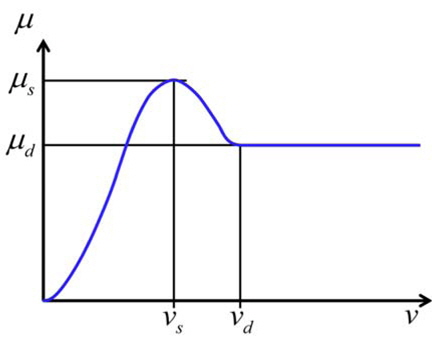
마찰계수를 Fig. 6과 같이 연속함수로 나타내면 적분 안정성을 보장할 수 있다. 그러나 연속함수의 특성상 두 물체간 상대속도가 없다면 마찰력 또한 없으므로 마찰력이 작용하며 정지해 있는, 즉 점착(stick)을 구현할 수 없을 뿐 아니라 물체가 vs 이하의 미세한 상대속도로 미끄러지는 문제가 있다.
타워크레인을 트랜스포터로 운송 시 경사면 각도가 미소할 뿐 아니라 웨이트 발라스트 블록으로 포탈베이스를 눌러주며 타워크레인의 포탈베이스와 트랜스포터 사이에 고무 패드를 사용해 미끄러지지 않게 한다. 따라서 타워크레인이 미끄러지는 경우는 실제 현상에서 관측되지 않는다. 그런데 위 마찰력 계산 방법을 사용해 시뮬레이션 하면 실제 현상과 달리 타워크레인이 미끄러지는 결과를 얻게 된다. 일반 해석 시에는 미세한 상대속도를 무시할 수도 있으나, 타워크레인 이동해석의 경우 와이어 로프 장력이 증가하는 결과를 얻게 되므로 바람직하지 않다.
일반적인 마찰력 계산 방법에 가상의 스프링 및 감쇄력을 이용해 점착 현상을 모사하는 방법이 제안되었으나 (Choi & Yoo,2012) 본 논문의 대상과 같이 타워크레인과 트랜스포터가 와이어 로프로 구속되어 있는 경우 와이어 로프의 장력이 이 가상의 스프링 및 감쇄력의 영향을 받아 진동하므로 부적합하다. 따라서 타워크레인이 넘어지는 현상을 시뮬레이션 할 수 있도록 타워크레인과 트랜스포터 사이에 적절한 구속 조건(constraints)을 고려하였다.
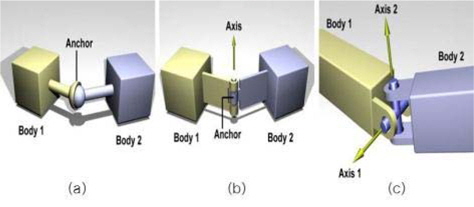
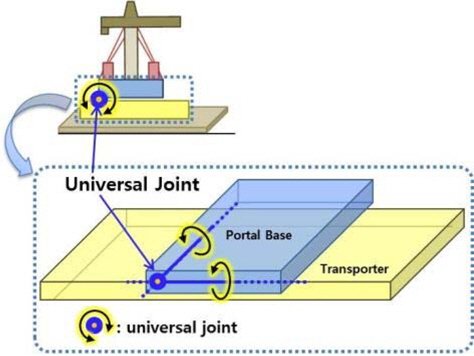
기구학(kinematics)의 구속 조건 중 회전 자유도 관련 조인트(joint)는 Fig. 7(a), (b), (c)와 같이 볼(ball) 조인트, 힌지(hinge) 조인트, 유니버설(universal) 조인트 등이 있다. 볼 조인트는 두 물체간 3축 회전 자유도, 힌지 조인트는 두 물체간 1축 화전, 유니버설 조인트는 두 물체간 2축 회전 자유도가 있는 경우다(Smith, 2006).
타워크레인의 포탈베이스 접촉면에 조인트를 추가 시, 볼 조인트는 두 접촉면의 상대 회전운동이 가능하므로 포탈베이스가 미끄러지며 회전하는 현상이 나타난다. 힌지 조인트는 한쪽 방향의 기울어짐만 표현 가능하므로 종 경사 및 횡 경사로 인해 두 방향으로 기울어지는 문제를 표현하기 어렵다. 따라서 본 논문에서는 Fig. 8의 조인트 연결지점에서 위치가 구속되어 미끄러지는 현상을 방지하고, 두 축을 따라 종 방향 및 횡 방향으로 전복 가능하도록 유니버설 조인트를 추가하였다.
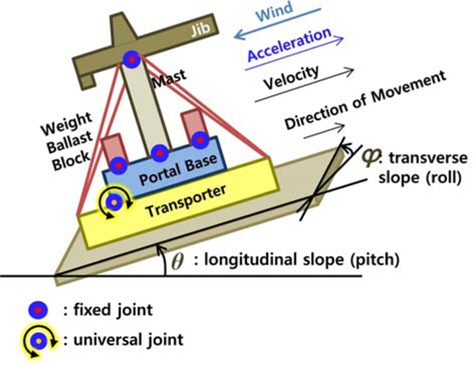
타워크레인의 무게중심은 마스트 중심 기준으로 뒤편에 위치하므로 뒤로 기울어지기 쉽다. 따라서 다음 상황일 때 타워크레인이 기울어지거나 전복될 가능성이 있다.
- 타워크레인에 풍력이 전진 방향과 반대로 작용 - 트랜스포터가 평지 및 양의 종 경사에서 이동 시작하는 경우 - 트랜스포터가 각도가 증가하는 종 경사면을 따라 올라가는 경우
이를 검토하기 위해 Fig. 9와 같이 트랜스포터의 속도, 가속도 방향은 양으로, 바람 방향은 반대방향으로, 종 경사는 양으로 설정하였다. 횡 방향 질량분포는 대칭이므로 횡 경사는 Fig. 9와 같이 설정하였다.
트랜스포터의 평지 및 경사면 이동 시뮬레이션을 위해 다음의 가정을 추가하였다.
- 경사면은 평지 또는 양의 종 경사로 설정 - 트랜스포터의 가속 방향은 전진 방향과 동일 - 풍력은 전진 방향과 반대로 일정하게 작용하는 것으로 가정
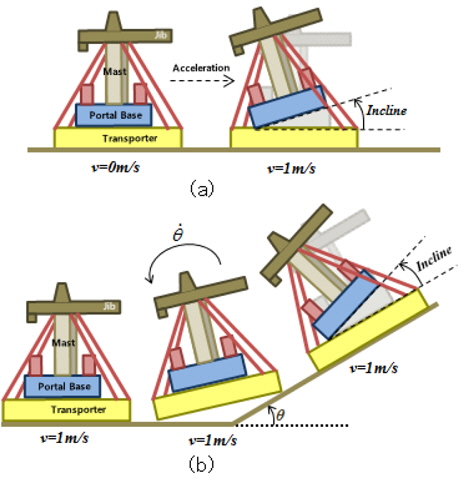
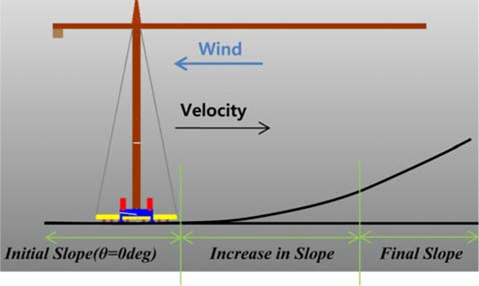
트랜스포터가 평지 및 양의 종 경사에서 출발하는 경우 타워크레인이 기울어지거나 전복될 가능성이 있다. 이 때 종 경사가 함께 변할 수 있으나 가속 소요시간이 길지 않아 변화량은 작다. 따라서 Fig. 10(a)와 같이 주어진 경사에서 이동 시작하는 경우와 Fig. 10(b)와 같이 일정 속도로 이동 중 경사가 변화하는 경우를 분리해 검토한다.
경사가 변화하는 경우 경사면 각도가 불연속적으로 변할 수 있으나, Fig. 10(b)와 같이 트랜스포터가 경사를 따라 올라가므로 트랜스포터 자체의 자세 변화는 불연속적이지 않다. 따라서 종 경사 변경 시 경사각은 평지에서 시작해 트랜스포터가 자체 길이만큼 진행하였을 때 최종 경사각과 동일해지며, 종 경사 변경 구간에서 트랜스포터에 일정 각 속도가 작용한다고 가정하여 모델링 하였다. 즉, 종 경사 변경 전과 후의 각 속도는 0이며 종 경사 시작 및 종료 시에 각 가속도가 작용하고, 종 경사 변경 중의 각 속도는 일정하다.
시뮬레이션 시나리오(scenario)는 다음과 같다
1) 시나리오 1: 트랜스포터 이동 시작
- 지면에 초기 횡 경사(0도, 2도) 및 초기 종 경사(0도, 3도, 5도) 부여 - 트랜스포터는 정지 상태에서 출발하여 목표 이동 속도(1m/s) 까지 일정하게 가속 - 가속도를 변화시켜 타워크레인이 기울어지는 현상 확인
2) 시나리오 2: 트랜스포터 이동 중 종 경사 변경
- 지면에 초기 횡 경사(0도, 2도) 부여 - 트랜스포터가 등속도(1 m/s)로 이동 중 각 가속도를 부여하여 종 경사를 0도에서 최종 종 경사까지 일정 각 가속도로 변경 - 각속도 변화에 따른 타워크레인의 전복 임계 경사각 확인 및 와이어 로프 장력 확인
이 때 경사변화시간은 트랜스포터 길이만큼 등속도로 이동하는 데 소요되는 시간으로 가정한다.
본 장에서는 3.2의 모델과 3.3의 시나리오를 적용하여 상용 S/W로 타워크레인의 운송을 시뮬레이션 한다. 시뮬레이션 결과로 운송 안정성을 검토하고 모델링의 타당성을 검증한다.
타워크레인의 총 질량(
rC/T=[−0.764 0.000 20.600]T rH/T=[−4.370 −3.000 2.050]T
본 시나리오에서는 트랜스포터의 선가속도로 인해 타워크레인에 관성력이 작용한다. 따라서 초기 횡 경사 및 초기 종 경사 조건 별로 정지상태에서 선 속도(1 m/s)까지 가속 소요시간을 조정함으로 선가속도를 바꾸어, 해당 조건에서 타워크레인이 기울어지는 선가속도를 찾는다.
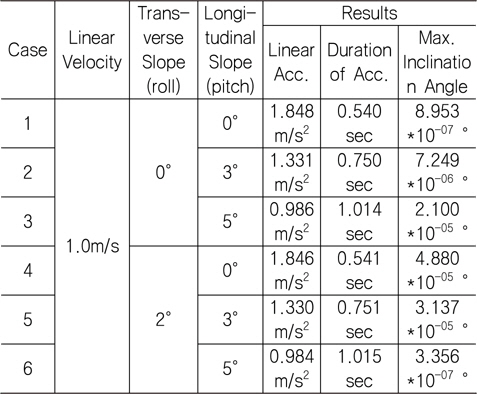
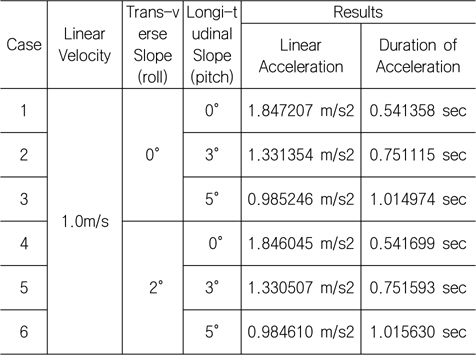
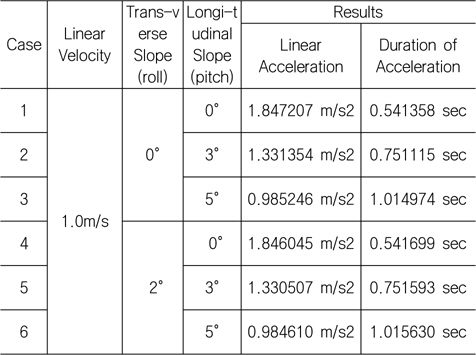
상용 다물체 동역학 해석 프로그램인 Recurdyn (Functionbay, 2012)으로 시뮬레이션 한 결과는 Table 1과 같다.
[Table 1] Simulation results for linear velocity change
Simulation results for linear velocity change
트랜스포터가 계산한 가속 소요시간 이상으로 가속하면(선가속도 이하로 가속) 타워크레인은 기울어지지 않는다. 계산한 가속 소요시간으로 가속 시 관성력에 의한 모멘트로 타워크레인이 기울어나 제자리로 돌아오며 그 기울기는 약 10-5도 이내로 미소하다. 그 이유는 가속 소요시간이 짧아 관성력이 작용하는 시간이 짧기 때문이다. 따라서 트랜스포터 출발 시 가속구간(가속 소요시간)에 의한 영향은 작다고 할 수 있다.
4.3 시나리오 2: 트랜스포터 이동 중 종 경사 변경
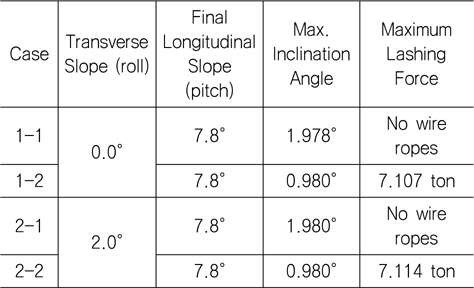
트랜스포터가 등 선 속도로 이동 중, 초기 종 경사 0도부터 시작해 경사가 증가하는 구간을 지나갈 때 타워크레인과 트랜스포터는 등 각속도 운동을 한다. 이후 트랜스포터는 일정 종 경사를 이동하나, 타워크레인은 각속도가 있기 때문에 경사 변화구간이 지난 후 타워크레인이 기울어진다. 따라서 여러 종 경사 조건 중 타워크레인이 기울어지나 제자리로 돌아오는, 즉 타워크레인이 전복되기 직전의 종 경사를 시뮬레이션으로 확인하였고, 그 결과는 Table 2와 같다.
[Table 2] Simulation results for linear angle change
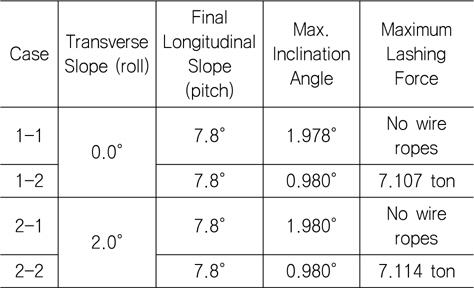
Simulation results for linear angle change
계산 결과, 트랜스포터가 최종 종 경사(7.8도) 이하로 이동하면 타워크레인이 최대 1.980도 기울어지나 제자리로 돌아온다. 트랜스포터가 최종 종 경사를 초과한 각도에서 이동하면 타워크레인이 전복될 수 있다. Case 1-1과 1-2를 비교하면 와이어 로프를 설치 시 최종 종 경사에 미치는 영향은 작으나 최대 기울어지는 각도는 0.980도로 줄어든다. Case 1-1과 2-1을 비교하면 횡 경사 2도가 최종 종 경사에 미치는 영향은 작은 것으로 나타났다.
트랜스포터와의 상대운동을 고려해 타워크레인의 운동방정식을 구성하고, 3.3의 시나리오 1과 같이 트랜스포터 이동 시작 시 타워크레인이 기울어지게 하는 임계 선가속도를 계산 후 정지상태에서 선 속도(1 m/s)까지 가속 소요시간을 계산하였다. 그 결과를 4.1의 상용 시뮬레이션 S/W 결과와 비교해 모델링의 타당성을 검증하였다.
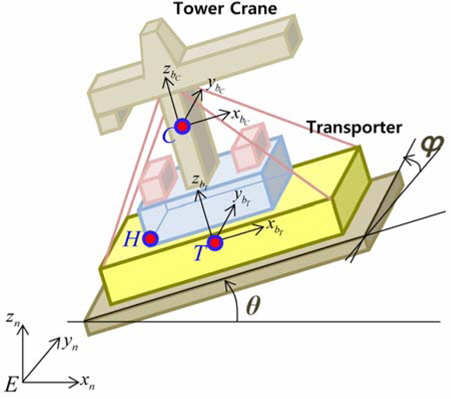
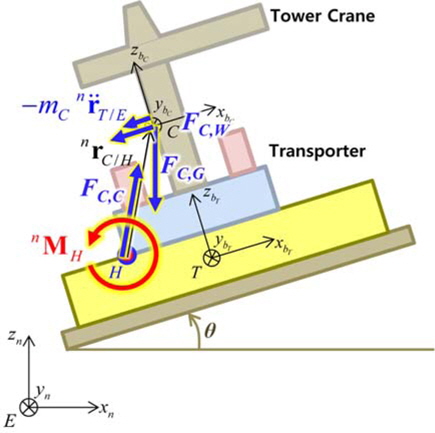
트랜스포터 및 타워크레인의 무게중심, 유니버설 조인트의 위치 등을 기술하기 위한 좌표계로 Fig. 13과 같이 관성 좌표계(inertial reference frame, n-frame)를 설정하고, 물체 고정 좌표계(body-fixed reference frame)로 타워크레인 무게중심 C와 트랜스포터 무게중심 T에 각각 타워크레인 고정 좌표계(tower crane fixed frame, bC-frame), 트랜스포터 고정 좌표계(transporter fixed frame, bT-frame)를 설정하였다.
관성 좌표계(n-frame)의 원점 E를 기준으로 정의한 점 C의 위치 벡터 rC/E는 식 (3)과 같이 트랜스포터 고정 좌표계(bT-frame)의 병진 위치 rT/E, 트랜스포터 고정 좌표계를 기준으로 한 유니버셜 조인트 H의 위치 rH/T, 점 H의 위치를 기준으로 타워크레인 고정 좌표계(bC-frame)의 병진 위치 r
여기서
타워크레인의 가속도 는 식 (3)을 이용 및 트랜스포터와 타워크레인의 병진운동을 고려하면 식 (4)와 같다.
n-frame을 기준으로 기술한 타워크레인의 운동방정식은 식 (5)과 같다.
여기서
식 (5)의 좌변을 식 (4) 로 치환하고, H점 기준으로 기술한 C의 가속도 외의 항을 우변으로 이항하면 식 (6)과 같다.
여기서, 은 트랜스포터 이동 시작 시, 타워크레인에 작용하는 관성력이다. 타워크레인에 작용하는 외력
유니버설 조인트의 위치 H를 기준으로 타워크레인에 작용하는 모멘트는 식 (7)과 같다.
여기서,
트랜스포터와 타워크레인이 회전 운동 시 관성 좌표계로 위치 벡터, 관성력, 풍력을 기술하면 시간에 따라 값이 변한다. 따라서 식 (7)을 트랜스포터의 물체 기준 좌표계로 변환하여 표현하면 식 (8)와 같다.
여기서,
식 (8)에 식(9), (10), (11), (12)를 대입해 모멘트
총 모멘트
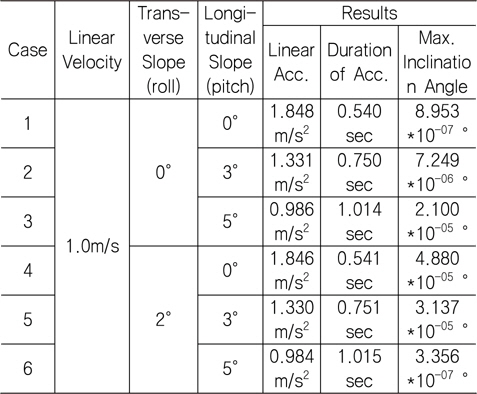
4.1의 값을 식 (14)에 대입하고, 시뮬레이션 case 별 종 경사 및 횡 경사를 대입하여 선가속도 구한 후 최종 선 속도(1 m/s)를 선가속도로 나누면 가속 소요시간을 계산할 수 있다. 수 계산 결과는 Table 3과 같다.
[Table 3] Analytic results for linear velocity change
Analytic results for linear velocity change
계산 결과, 타워크레인이 기울어지는 선가속도 및 가속 소요시간 수 계산 결과는 Table 1의 시뮬레이션 결과와 거의 유사하다. 따라서 타워크레인의 운송 시뮬레이션을 위해 사용한 모델링 방법이 타당하다고 판단된다.
본 논문에서는 공법 설계자가 타워크레인 운송 중 타워크레인 거동 안정성 분석 결과를 도출하기에 적합한 모델링 방법을 검토하고, 이를 적용하여 시뮬레이션 하였으며 동역학 계산을 통해 결과를 비교하였다.
모델링 방법으로 타워크레인과 트랜스포터의 접촉면을 모사할 때 물체간 접촉력을 포함하고, 두 물체간 점착 현상을 모사하기 위해 마찰력 대신 타워크레인과 트랜스포터 사이에 구속조건을 추가하였다. 구속조건으로 타워크레인과 트랜스포터의 접촉면의 모서리를 따라 종 방향 및 횡 방향으로 기울어질 수 있도록 유니버설 조인트를 추가하였다.
트랜스포터의 평지 및 경사면 이동을 모사하기 위해 트랜스포터가 이동 시작, 트랜스포터 이동 중 종 경사를 변경하는 경우를 나누어 정리하고, 시뮬레이션을 수행하였다. 모델링 결과의 검증 시 현장 계측 데이터의 확보 및 비교가 어려운 관계로, 트랜스포터 이동 시작 경우의 수 계산 결과와 시뮬레이션 결과를 비교하여 모델링 방법의 타당성을 검증하였다. 이러한 모델링 방법을 적용하면 타워크레인의 운송 안정성 검토에 유용할 것으로 기대된다. 다만, 본 논문에서 제시한 모델링 방법은 모델링 가정에서 언급한 바와 같이 트랜스포터의 타이어 유압시스템, 지면의 거칠기, 타워크레인 마스트와 지브의 유연체 거동 등은 고려하지 않았으므로 향후 이러한 영향을 추가로 고려한 연구가 필요하다.