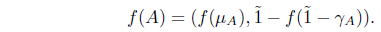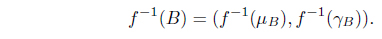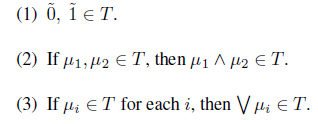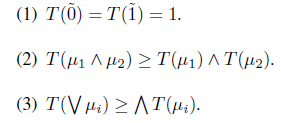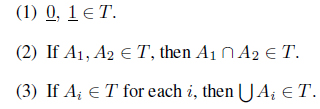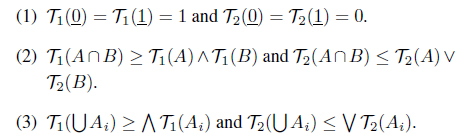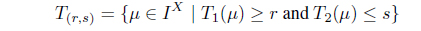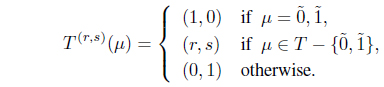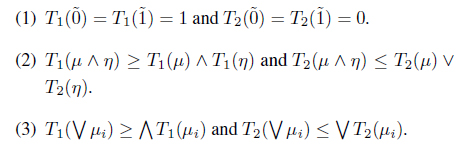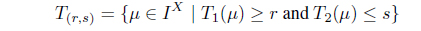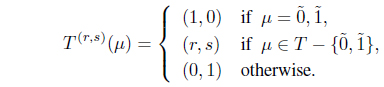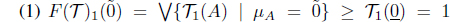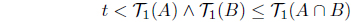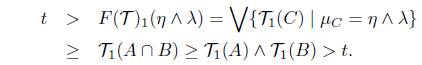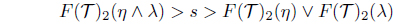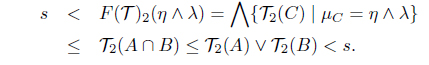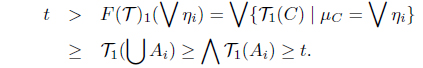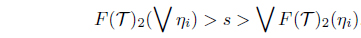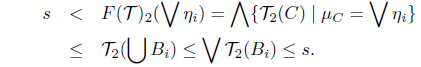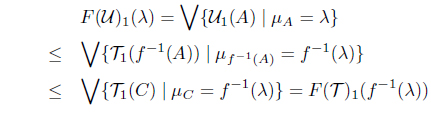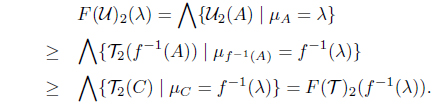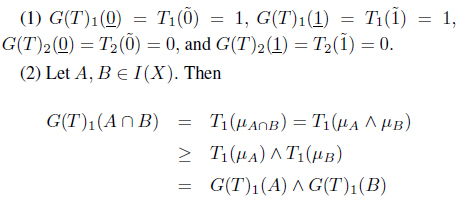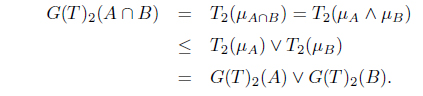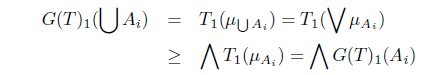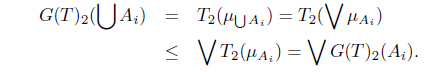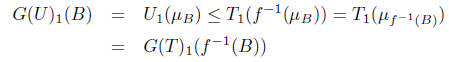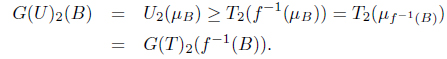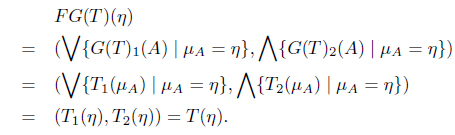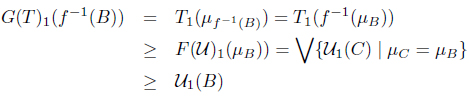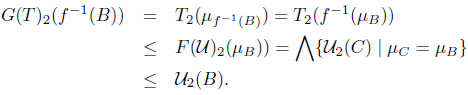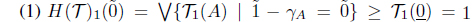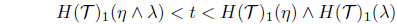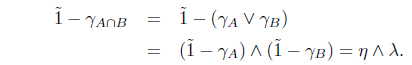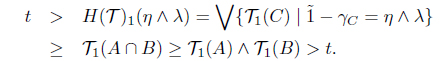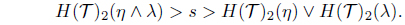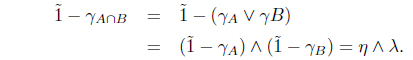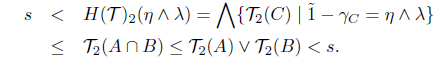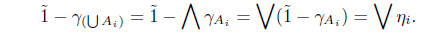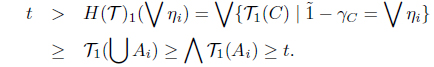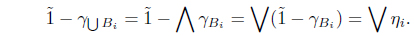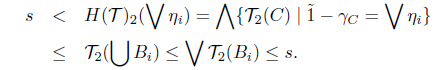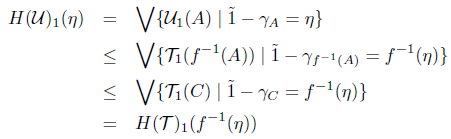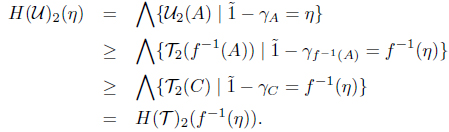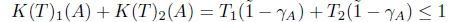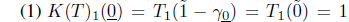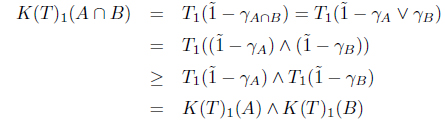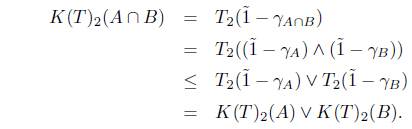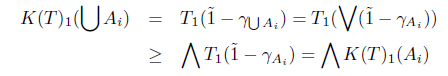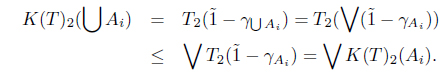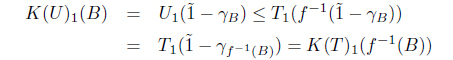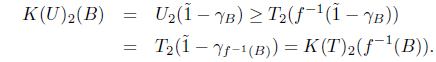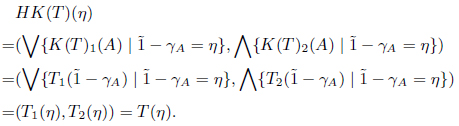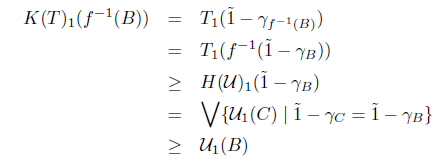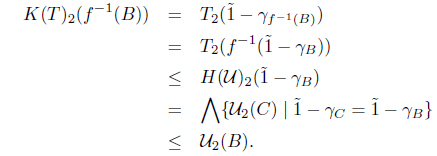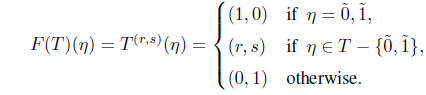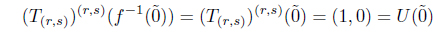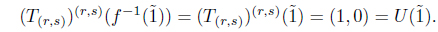We will denote the unit interval [0, 1] of the real line by I. A member μ of I X is called a fuzzy set in X. By and we denote the constant fuzzy sets in X with value 0 and 1, respectively. For any μ ∈ IX, μc denotes the complement .
Let X be a nonempty set. An intuitionistic fuzzy set A is an ordered pair
where the functions μA : X → I and γA : X → I denote the degree of membership and the degree of nonmembership, respectively and μA + γA ≤ 1. By and we denote the constant intuitionistic fuzzy sets with value (0, 1) and (1, 0), respectively. Obviously every fuzzy set μ in X is an intuitionistic fuzzy set of the form (μ, ).
Let f be a mapping from a set X to a set Y . Let A = (µA, γA) be an intuitionistic fuzzy set in X and B = (µB, γB) an intuitionistic fuzzy set in Y . Then
(1) The image of A under f, denoted by f(A), is an intuitionistic fuzzy set in Y defined by
(2) The inverse image of B under f, denoted by f−1 (B), is an intuitionistic fuzzy set in X defined by
All other notations are standard notations of fuzzy set theory.
Definition 2.1. ( [2]) A Chang’s fuzzy topology on X is a family T of fuzzy sets in X which satisfies the following properties:
The pair (X, T) is called a fuzzy topological space.
Definition 2.2. ( [9]) A smooth topology on X is a mapping T : IX → I which satisfies the following properties:
The pair (X, T) is called a smooth topological space.
Definition 2.3. ( [4]) An intuitionistic fuzzy topology on X is a family T of intuitionistic fuzzy sets in X which satisfies the following properties:
The pair (X, T) is called an intuitionistic fuzzy topological space.
Let I(X) be a family of all intuitionistic fuzzy sets in X and let I ⊗ I be the set of the pair (r, s) such that r, s ∈ I and r + s ≤ 1.
Definition 2.4. ( [5]) Let X be a nonempty set. An intuitionistic fuzzy topology in Ŝostak’s sense (SoIFT for short) 𝒯 = (𝒯1, 𝒯2) on X is a mapping 𝒯 : I(X) → I ⊗ I which satisfies the following properties:
Then (X, 𝒯) = (X, 𝒯1, 𝒯2) is said to be an intuitionistic fuzzy topological space in Ŝostak’s sense (SoIFTS for short). Also, we call 𝒯1(A) the gradation of openness of A and 𝒯2(A) the gradation of nonopenness of A.
Definition 2.5. ([5]) Let f : (X, 𝒯1, 𝒯2) → (Y, 𝒰1, 𝒰2) be a mapping from a SoIFTS X to a SoIFTS Y. Then f is said to be SoIF continuous if 𝒯1(f−1(B)) ≥ 𝒯1(B) and 𝒯2(f−1(B)) ≤ 𝒯2(B) for each B ∈ I(Y ).
Let (X, 𝒯) be a SoIFTS. Then for each (r, s) ∈ I ⊗ I, the family 𝒯(r,s) defined by
is an intuitionistic fuzzy topology on X. In this case, 𝒯(r,s) is called the (r, s)-level intuitionistic fuzzy topology on X.
Let (X, T) be an intuitionistic fuzzy topological space. Then for each (r, s) ∈ I ⊗ I, a SoIFT T(r,s) : I(X) → I ⊗ I defined by
In this case, T (r,s) is called an (r, s)-th graded SoIFT on X and (X, T(r,s)) is called an (r, s)-th graded SoIFTS on X.
Definition 2.6. ([7]) Let X be a nonempty set. An intuitionistic fuzzy topology in Mondal and Samanta’s sense(MSIFT for short) T = (T1, T2) on X is a mapping T : IX → I ⊗ I which satisfy the following properties:
Then (X, T) is said to be an intuitionistic fuzzy topological space in Mondal and Samanta’s sense(MSIFTS for short). T1 and T2 may be interpreted as gradation of openness and gradation of nonopenness, respectively.
Definition 2.7. ([7]) Let f : (X, T1, T2) → (Y, U1, U2) be a mapping. Then f is said to be MSIF contiunous if T1(f−1(η)) ≥ U1(η) and T2(f−1(η)) ≤ U2(η) for each η ∈ IY.
Let (X, T) be a MSIFTS. Then for each (r, s) ∈ I ⊗ I, the family T(r,s) defined by
is a Chang’s fuzzy topology on X. In this case, T(r,s) is called the (r, s)-level Chang’s fuzzy topology on X.
Let (X, T) be a Chang’s fuzzy topological spaces. Then for each (r, s) ∈ I ⊗ I, a MSIFT T(r,s) : IX → I ⊗ I is defined by
In this case, T(r,s) is called an (r, s)-th graded MSIFT on X and (X, T(r,s)) is called an (r, s)-th graded MSIFTS on X.
Let MSIFTop be the category of all intuitionistic fuzzy topological spaces in Mondal and Samanta’s sense and MSIF continuous mappings, and let SoIFTop be the category of all intuitionistic fuzzy topological spaces in Ŝostak’s sense and SoIF continuous mappings.
Theorem 3.1. Define a functor F : SoIFTop → MSIFTop by F(X, 𝒯) = (X, F(𝒯)) and F(f) = f, where F(𝒯)(η) = (F(𝒯)1(η), F(𝒯)2(η)), F(𝒯)1(η) = ∨ {𝒯1(A) | µA = η}, F(𝒯)2(η) = ⋀ {𝒯2(A) | µA = η}. Then F is a functor.
Proof. First, we show that F(𝒯) is a MSIFT.
Clearly, F(𝒯)(η) = F(𝒯)1(η) + F(𝒯)2(η) ≤ 1 for any η ∈ IX.
(2) Suppose that F(𝒯)1(η ∧ λ) < F(𝒯)1(η) ∧ F(𝒯)1(λ). Then there is a t ∈ I such that F(𝒯)1(η∧λ) < t < F(𝒯)1(η) ∧ F(𝒯)1(λ). Since t < F(𝒯)1(η) = ∨ {T1(C) | µC = η}, there is an A ∈ I(X) such that t < 𝒯1(A) and µA = η. There is a B ∈ I(X) such that t < 𝒯1(B) and µB = λ, because t < F(𝒯)1(λ) = ∨{𝒯1(C) | µC = λ}. Thus t < 𝒯1(A) ∧ 𝒯1(B) and µA∩B = µA ∧ µB = η ∧ λ. Since 𝒯 is a SoIFT, we obtain
Hence
This is a contradiction. Thus F(𝒯)1(η ∧ λ) ≥ F(𝒯)1(η) ∧ F(𝒯)2(λ).
Next, assume that F(𝒯)2(η ∧ λ) > F(𝒯)2(η) ∨ F(𝒯)2(λ). Then there is an s ∈ I such that
Since s > F(𝒯)2(η) = ⋀{𝒯2(C) | µC = η}, there is an A ∈ I(X) such that s > 𝒯2(A) and µA = η. As s > F(𝒯)2(λ) = ⋀{𝒯2(C) | µC = λ}, there is a B ∈ I(X) such that s > 𝒯2(B) and µB = λ. So s > 𝒯2(A) ∨ 𝒯2(B) and µA∩B = µA ∧ µB = η ∧ λ. Since 𝒯 is a SoIFT, we have s > 𝒯2(A) ∨ 𝒯2(B) ≥ 𝒯2(A ∩ B). Thus
This is a contradiction. Hence F(𝒯)2(η ∧ λ) ≤ F(𝒯)2(η) ∨ F(𝒯)2(λ).
(3) Suppose that F(𝒯)1(∨ηi) < ⋀F(𝒯)1(ηi). Then there is a t ∈ I such that F(𝒯)1(∨ηi) < t < ⋀ F(𝒯)1(ηi). Since t < F(𝒯)1(ηi) = ∨ {T1(C) | µC = ηi} for each i, there is an Ai ∈ I(X) such that t < 𝒯1(Ai) and µAi = ηi. Thus t ≤ ⋀ 𝒯1(Ai) and µ∪ Ai = ∨µAi = ∨ηi. As 𝒯 is a SoIFT, we obtain 𝒯1(∪ Ai) ≥ ⋀ 𝒯1(Ai). Hence
This is a contradiction. Thus F(𝒯)1(∨ηi) ≥ ⋀F(𝒯)1(ηi).
Next, assume that F(𝒯)2(∨ηi) > ∨F(𝒯)2(ηi). Then there is an s ∈ I such that
Since s > F(𝒯)2(ηi) = ⋀{𝒯2(C) | µC = ηi} for each i, there is a Bi ∈ I(X) such that s > 𝒯2(Bi) and µBi = ηi. Hence s ≥ ∨𝒯2(Bi) and µ∪Bi = ∨µBi = ∨ηi. Since 𝒯 is a SoIFT, we have 𝒯2(∪Bi) ≤ ∨𝒯2(Bi). Thus
This is a contradiction. Hence F(𝒯)2( ∨ ηi) ≤ ∨F(𝒯)2(ηi). Therefore (X, F(𝒯)) is a MSIFTS.
Finally, we show that if f : (X, 𝒯) → (Y, 𝒰) is SoIF continuous, then f : (X, F(𝒯)) → (Y, F(𝒰)) is MSIF continuous. Let F(𝒯) = (F(𝒯)1, F(𝒯)2), F(𝒰) = (F(𝒰)1, F(𝒰)2), and λ ∈ IY . Then
and
Therefore F is a functor.
Theorem 3.2. Define a functor G : MSIFTop → SoIFTop by G(X, T) = (X, G(T)) and G(f) = f, where G(T)(A) = (G(T)1(A), G(T)2(A)), G(T)1(A) = T1(µA), and G(T)2(A) = T2(µA). Then G is a functor.
Proof. First, we show that G(T) is a SoIFT.
Clearly, G(T)1(A) + G(T)2(A) = T1(µA) + T2(µA) ≤ 1 for any A ∈ I(X).
and
(3) Let Ai ∈ I(X) for each i. Then
and
Hence (X, G(T)) is a SoIFT.
Next, we show that if f : (X, T) → (Y, U) is MSIF continuous, then f : (X, G(T)) → (Y, G(U)) is SoIF continuous. Let B = (µB, γB) ∈ I(Y ). Then
and
Thus f : (X, G(T)) → (Y, G(U)) is SoIF continuous. Consequently, G is a functor.
Theorem 3.3. The functor G : MSIFTop → SoIFTop is a left adjoint of F : SoIFTop → MSIFTop.
Proof. Let (X, T) be an object in MSIFTop and η ∈ I X. Then
Hence lX : (X, T) → FG(X, T) = (X, T) is MSIF continuous.
Consider (Y, 𝒰) ∈ SoIFTop and a MSIF continuous mapping f : (X, T) → F(Y, 𝒰). In order to show that f : G(X, T) → (Y, 𝒰) is a SoIF continuous mapping, let B ∈ I(Y). Then
and
Hence f : (X, G(T)1, G(T)2) → (Y, 𝒰1, 𝒰2) is a SoIF continuous mapping. Therefore lX is a G-universal mapping for (X, T) in MSIFTop.
Theorem 3.4. Define a functor H : SoIFTop → MSIFTop by H(X, 𝒯) = (X, H(𝒯)) and H(f) = f, where , and . Then H is a functor.
Proof. First, we show that H(𝒯) is a MSIFT. Obviously, H(𝒯)(η) = H(𝒯)1(η) + H(𝒯)2(η) ≤ 1 for any η ∈ IX.
(2) Assume that H(𝒯)1(η ∧ λ) < H(𝒯)1(η) ∧ H(𝒯)1(λ). Then there is a t ∈ I such that
As , there is an A ∈ I(X) such that . Since , there is a B ∈ I(X) such that and
Since 𝒯 is a SoIFT, t < 𝒯1(A) ∧ 𝒯1(B) ≤ 𝒯1(A ∩ B). Thus
This is a contradiction. Hence H(𝒯)1(η ∧ λ) ≥ H(𝒯)1(η) ∧ H(𝒯)1(λ).
Suppose that H(𝒯)2(η∧λ) > H(𝒯)2(η)∨H(𝒯)2(λ). Then there is an s ∈ I such that
Since , there is an A ∈ I(X) such that s > 𝒯2(A) and . As , there is a B ∈ I(X) such that s > 𝒯2(B) and . So s > 𝒯2(A) ∨ 𝒯2(B) and
Since 𝒯 is a SoIFT, we obtain s > 𝒯2(A)∨𝒯2(B) ≥ 𝒯2(A∩B). Hence
This is a contradiction. Thus H(𝒯)2(η ∧ λ) ≤ H(𝒯)2(η) ∨ H(𝒯)2(λ).
(3) Assume that H(𝒯)1(∨ηi) < ⋀H(𝒯)1(ηi). Then there is a t ∈ I such that
H(𝒯)1(∨ηi) < t < ⋀H(𝒯)1(ηi).
As for each i, there is an Ai ∈ I(X) such that t < 𝒯1(Ai) and . Hence t ≤ ⋀𝒯1(Ai) and
Since 𝒯 is a SoIFT, we have 𝒯1(∪Ai) ≥ ⋀𝒯1(Ai). Thus
This is a contradiction. Hence H(𝒯)1(∨ηi) ≥ ⋀H(𝒯)1(ηi).
Suppose that H(𝒯)2(∨ηi) > ∨H(𝒯)2(ηi). Then there is an s ∈ I such that H(𝒯)2(∨ηi) > s > ∨H(𝒯)2(ηi). Since for each i, there is a Bi ∈ I(X) such that s > 𝒯2(Bi) and . Hence s ≥ ∨𝒯2(Bi) and
We have 𝒯2(∪Bi) ≤ ∨𝒯2(Bi) because 𝒯 is a SoIFT. Thus
This is a contradiction. Hence H(𝒯)2( ∨ ηi) ≤ ∨H(𝒯)2(ηi). Therefore (X, H(𝒯)) is a MSIFTS.
Next, we show that if f : (X, 𝒯) → (Y, 𝒰) is SoIF continuous, then f : (X, H(𝒯)) → (Y, H(𝒰)) is MSIF continuous. Let H(𝒯) = (H(𝒯)1, H(𝒯)2), H(𝒰) = (H(𝒰)1, H(𝒰)2), and η ∈ IX. Then
and
Therefore H is a functor.
Theorem 3.5. Define a functor K : MSIFTop → SoIFTop by K(X, T) = (X, K(T)) and K(f) = f, where K(T) = (K(T)1, K(T)2), , and . Then K is a functor.
Proof. First, we show that K(T) is a SoIFT. Clearly,
for any A ∈ I(X).
(2) Let A, B ∈ I(X). Then
and
(3) Let Ai ∈ I(X) for each i. Then
and
Thus (X, K(T)) is a SoIFTS.
Finally, we show that if f : (X, T) → (Y, U) is MSIF continuous, then f : (X, K(T)) → (Y, K(U)) is SoIF continuous. Let B = (µB, γB) ∈ I(Y). Then
and
Hence f : (X, K(T)) → (Y, K(U)) is SoIF continuous. Consequently, K is a functor.
Theorem 3.6. The functor K : MSIFTop → SoIFTop is a left adjoint of H : SoIFTop → MSIFTop.
Proof. For any (X, T) in MSIFTop and η ∈ IX,
Hence lX : (X, T) → HK(X, T) = (X, T) is a MSIF continuous mapping. Consider (Y, 𝒰) ∈ SoIFTop and a MSIF continuous mapping f : (X, T) → H(Y, 𝒰). In order to show that f : K(X, T) → (Y, 𝒰) is a SoIF continuous mapping, let B ∈ I(Y). Then
and
Thus f : (X, K(T)) → (Y, 𝒰) is SoIF continuous. Hence lX is a K-universal mapping for (X, T) in MSIFTop.
Let (r, s)-gMSIFTop be the category of all (r, s)-th graded intuitionistic fuzzy topological spaces in Mondal and Samanta’s sense and MSIF continuous mappings, and let CFTop be the category of all Chang’s fuzzy topological spaces and fuzzy continuous mappings.
Theorem 3.7. Two categories CFTop and (r, s)-gMSIFTop are isomorphic.
Proof. Define F : CFTop → (r, s)-gMSIFTop by F(X, T) = (X, F(T)) and F(f) = f, where
Define G : (r, s)-gMSIFTop → CFTop by G(X, 𝒯) = (X, G(𝒯)) and G(f) = f, where
G(𝒯) = 𝒯(r,s) = {η ∈ IX | 𝒯1(η) ≥ r and 𝒯2(η) ≤ s}.
Then F and G are functors. Obviously, GF(T) = G(T(r,s)) = (T(r,s))(r,s) = T and FG(T) = F(𝒯(r,s)) = (𝒯(r,s))(r,s) = 𝒯. Hence CFTop and (r, s)-gMSIFTop are isomorphic.
Theorem 3.8. The category (r, s)-gMSIFTop is a bireflective full subcategory of MSIFTop.
Proof. Obviously, (r, s)-gMSIFTop is a full subcategory of MSIFTop. Let (X, T) be an object of MSIFTop. Then for each (r, s) ∈ I ⊗ I, (X, (T(r,s))(r,s)) is an object of (r, s)-gMSIFTop and lX : (X, T) → (X, (T(r,s))(r,s)) is a MSIF continuous mapping. Let (Y, U) be an object of the category (r, s)-gMSIFTop and f : (X, T) → (Y, U) a MSIF continuous mapping. we need only to check that f : (X, (T(r,s))(r,s)) → (Y, U) is a MSIF continuous mapping. Since (Y, U) ∈ (r, s)-gMSIFTop, U(η) = (1, 0), (r, s), or (0, 1). Let U(η) = (1, 0). Then or . In fact,
and
In case U(η) = (0, 1), clearly U(η) ≤ (T(r,s))(r,s) (f−1 (η)). Let U(η) = (r, s). Since f : (X, T) → (Y, U) is MSIF continuous, T(f−1 (η)) ≥ U(η) = (r, s). Thus f−1 (η) ∈ T(r,s), and hence (T(r,s))(r,s) (f−1 (η)) = (r, s) = U(η). Therefore f : (X, (T(r,s))(r,s)) → (Y, U) is a MSIF continuous mapping.
From the above theorems, we have the follwing main result.
Theorem 3.9. The category CFTop is a bireflective full subcategory of MSIFTop.