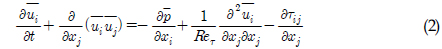최근 심해 해양자원 개발의 확대로 인해 석유와 가스 시추를 위한 해저 석유 생산용 라이저(riser)와 부유체 구조물들의 설치 수요가 증가하고 있다. 이러한 구조물들은 기본적으로 뭉툭한(Bluff) 형상을 지니고 있기 때문에 조류 변화로 인해 주기적인 와흘림과 함께 와유기 진동(Vortex induced vibration, VIV)을 겪게 된다. 특히 와유기 진동은 구조물에 공진현상을 일으킬 수 있기 때문에 공학적 설계에 있어서 주요 연구 대상이 되어 왔다. 그 성과로서 해양 구조물의 와유기 진동 및 저항 저감을 위해 수동제어 방법이 고려된 나선형 스트레이크(Helical strake) 및 파형 실린더(Wavy cylinder)가 소개되었으며 효과 또한 입증되었다(Ahmed and Bays-muchmore, 1992; Nebres et al., 1993; Chyu and Rockwell, 1996; Lam et al., 2004a; Lam et al., 2004b; Lee and Nguyen, 2007; Lam and Lin, 2008).
해양 구조물들의 기본 형상이 되는 원형 실린더에 관한 논문들에 대해 포괄적 연구를 수행한 Williamson(1996)에 따르면, 원형 실린더의 항력과 양력의 특성은 Reynolds number(Re)와 일정한 관계를 가지지 않고 달라진다. 아임계(Subcritical)영역의 경우, Re가 대략 300에서 1,000까지 증가할 때 실린더 배면(Base)에서의 음압과 레이놀즈 응력(Reynolds stress)의 레벨이 감소하여 실린더의 항력과 양력도 감소하지만, Re가 1,000 이상이 되면 그 특성은 반대가 되어 실린더의 항력과 양력은 증가하게 된다. 또 와류 형성 길이(Vortex formation length)가 감소하게 됨에 따라 Strouhal number는 점진적으로 감소하는 것으로 보고하였다. 즉 많은 선행 연구들을 통해서 원형 실린더의 유동 및 항력과 양력 특성은 Re 변화에 의존하고 있는 것을 알 수 있다(Unal and Rockwell, 1988; Prasad and Williamson, 1997; Norberg, 1998, Dong et al., 2006).
최근 해양 구조물의 와유기 진동 및 저항 저감을 위한 또 다른 수동 제어기법인 해양구조물에 나선형 표면 처리를 한 트위스트 실린더(Twisted cyliner)에 대한 연구가 진행되었고, 원형 구조물과 비교하여 저항과 와유기 진동이 약 15% 및 96%가 각각 감소된 것을 보고하였다(Jung et al., 2012). 그러나 나선형 해양 구조물(이하 트위스트 실린더, twisted Cylinder)의 경우, 저자들이 조사한 바로는Re 변화에 따른 유동 특성 연구가 대단히 중요함에도 불구하고 Re=3,000에서 수행된 Jung et al.(2012)의 연구 외에는 관련 연구가 전무한 것으로 판단하고 있다. 따라서 트위스트 실린더에 대해 Re 영향성 평가를 실시하여 트위스트 실린더 주위 유동 및 항력과 양력 특성을 연구하는 것은 대단히 중요하다고 생각된다.
본 연구에서는 대형와모사법(Large eddy simulation, LES)을 이용하여 아임계(Subcritical) 영역에 해당되는 3×103 < Re < 1×104에서 Re 변화에 따른 트위스트 실린더의 유동 특성과 와유기 및 저항 저감 특성에 관한 연구를 수행하였다. 또한 유동 특성 비교를 위해, 원형 구조물(이하 원형 실린더, Smooth cylinder)에 대한 유동장 계산도 함께 진행하였다. 해양 환경의 구현을 위해서는 초임계(Supercritical)영역 이상에 해당하는 Re를 고려하는 것이 옳은 일이나, 높은 Re영역에서 발생하는 난류특성, 특히 소규모 와동(Small scale eddy)들을 재현하기 위해 고려되는 격자들로 인해서 상당량의 계산 자원을 필요로 하므로 실용적인 측면에서 접근이 어려운 실정이다. 이와 반대로, 아임계 영역에서 수행된 수치해석 기반 연구들과 실험 연구들이 많이 진행되어져 왔으므로 신뢰성 있는 수치해석 결과를 얻을 수 있는 장점에 착안하여, 나선형 실린더 구조물에 대한 초기 연구로 아임계 영역에서 Re 효과에 관한 트위스트 실린더 연구를 진행하였다.
트위스트 실린더 주위 유동을 해석하기 위하여 고려되어진 지배방정식은 일정 물성치에 대한 비정상, 비압축성 유동해석에 대한 것으로, 격자 필터링이 되어진 연속 방정식 및 운동량 보존 방정식은 아래와 같다.
여기서 는 격자 필터링으로 얻어진 대형 스케일의 유동을 나타낸다, 식 (2)에서 τij는 Subgrid 스케일 유동이 대형 스케일 Rresolved scale) 유동에 미치는 영향을 나타내며 다음과 같이 표현되어진다.
여기서 Subgrid stress scale tensor τij 는 Germano et al.(1991)이 제안한 Dynamic model을 사용하여 구하였다. Dynamic Smagorinsky coefficient(Cs)가 음의 값을 가질 경우는 작은 스케일에서 큰 스케일로 에너지가 전달되는 backscatter 현상으로 간주된다. 하지만 이 음의 값은 식 (2)의 우변항의 에너지 증가로 인해 무한대로 발산하게 된다. 따라서 이 문제를 피하기 위하여 균질한(homogenous) 공간적인 방향에 대해 짧은 시간동안 평균 조작 또는 ad hoc clipping 등의 방법을 사용한다(Breuer, 1998; Breuer, 2000; Jordan and Ragab, 1998; Jordan, 2002). 하지만 이러한 방법들은 공간적으로 균질하지 않은 유동에 대해서는 제대로 작동되지 않을 수 있기 때문에, 본 연구에서는 간단한 방법으로 전체 계산 영역(Volume)에 대해 평균화 방법을 거쳐 Cs 값을 얻었다. 따라서 본 연구에서 Cs값은 단지 시간의 함수이다. 이 방법은 블레이드가 설치된 혼합 탱크 내 유동해석에 있어서 성공적으로 적용된바 있다(Yoon et al., 2009).
본 연구에서 지배방정식은 보존형 유한체적법(Conservative finite volume formulation)으로 이산화 되어졌다. 시간차분에 대해서 Time-splitting, 공간 차분은 2차 중앙 차분법을 적용하였다. 그리고 점성항은 2차 Crank-Nicolson 방법, 비선형항은 2차 Adams-Bathforth 방법을 사용하였다.
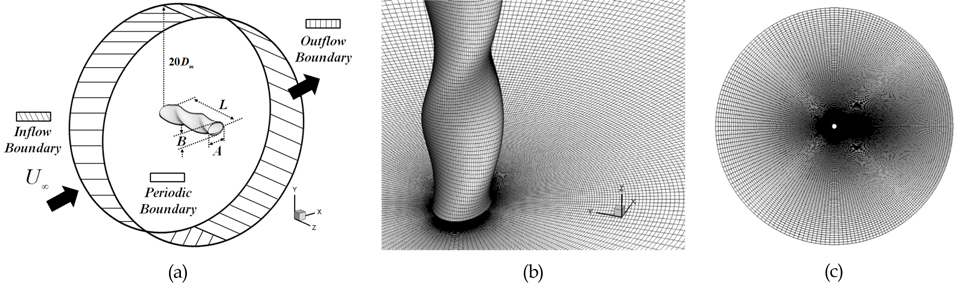
해석영역은 Fig. 1에 도시한 바와 같이 O-type의 격자를 사용하였으며 실린더 중심에서부터 경계면까지의 거리는 20Dm가 된다. 실린더 축방향 길이(L)는 4.55Dm이며, 이는 Lam and Lin (2008)이 고려한 축방향 길이와 일치한다. 여기서 Dm은 트위스트 실린더의 장축의 길이(A)와 단축의 길이(B)의 평균값을 의미한다. 유입부의 무차원화된 속도는 x방향 속도인 U∞ = 1이며, 축방향의 면은 주기조건을 부여하였다. 유출부의 경계조건으로 대류경계조건을 사용하였으며 이때의 대류속도는 출구평균속도를 적용하였다. 격자 생성에 있어서 첫 번째 격자 위치는 y+ = 1에 해당하는 값을 사용하였고 격자 증가 비율(Grid stretching ratio)은 1.2 이하로 고려하였다. 사용된 격자수는 Re변화에 따라 약 250-450만개를 사용하였다. 실린더 후류를 상세히 모사하기 위해 격자 분포를 실린더 후방에 집중하였으며 해석 영역의 유입구와 출구의 경계면을 기준으로 실린더 전방과 후방의 격자수를 3:7비율로 고려하였다. 이에 대한 격자 분포는 Fig. 1 (b)와 (c)에 나타내었다.
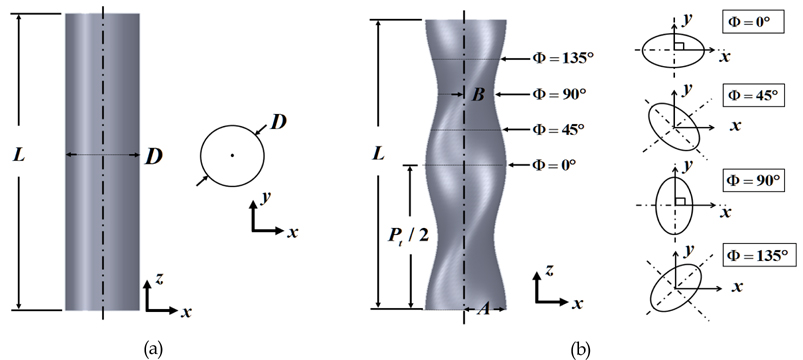
Fig. 2는 본 연구에서 고려되어진 두 가지 타입의 실린더를 나타낸다. 트위스트 실린더는 장축과 단축에 의해서 타원 단면이 결정되는데, 원형 실린더와의 비교를 위하여 장축의 길이(A)와 단축의 길이(B)의 평균값(Dm)은 원형실린더의 직경(D)과 동일하다. 트위스트 실린더의 상세한 모델 제원은 Jung et al.(2012)에서 고려한 것과 동일하다.
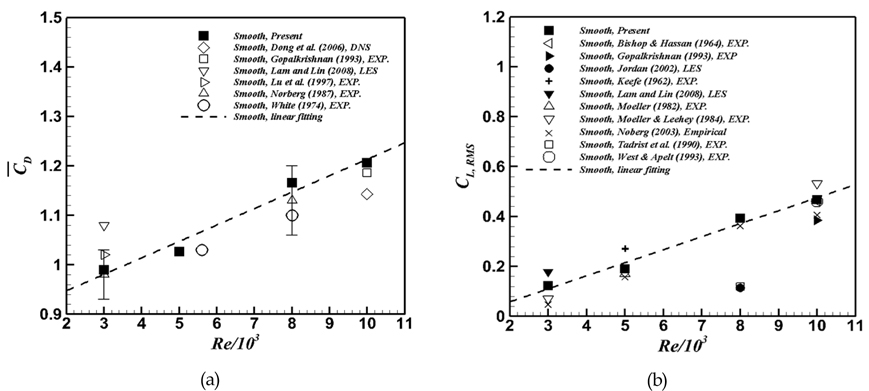
수치해석기법 및 해석결과의 신뢰성을 확보하기 위하여 원형 실린더에 대한 기존 선행연구들의 실험 및 수치해석결과들을(Keefe, 1962; Bishop and Hassan, 1964; White, 1974; Moeller, 1982; Moeller and Leehey, 1984; Norberg, 1987; Tadrist et al., 1990; Gopalkrishnan 1993; West and Apelt 1993; Jordan 2002; Norberg 2003; Dong et al., 2006; Lam and Lin 2008) 본 연구 결과와 비교하였으며 Fig. 3에 도시하였다. 항력과 양력 계수 값은 선행 연구들마다 다소 차이가 있지만 본 연구의 결과 값들은 선행 연구들의 결과 값들 사이에 위치하고 있는 것을 알 수 있다. 결과적으로, Re 증가에 따른 항력과 양력 변화 패턴이 선 행 연구들과 잘 일치함을 Fig. 3을 통해 확인할 수 있다.
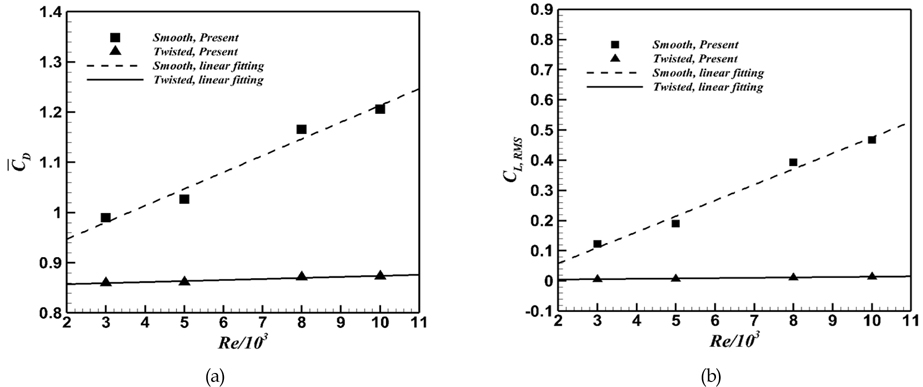
Re 변화에 따른 원형 및 트위스트 실린더의 항력 및 양 력 계수(CL,RMS)를 Fig. 4에 도시하였다. 원형 실린더의 경우, Re가 증가하면 항력과 양력 계수 값들이 같이 증가하는 것을 확인할 수 있다. 이러한 특성은 Re가 증가할 때 전단층의 불안정성(Shear layer instability)의 발달과 관계가 있다(Williamson, 1996). 이와 유사하게 트위스트 실린더 또한 Re가 증가하면 항력 및 앙력 계수 값들 또한 증가한다. 그러나 Re 증가에 따른 트위스트 실린더의 항력 및 양력 계수의 증가율은 원형 실린더의 그것들보다 현저히 낮은 것을 Fig. 4를 통해 확인할 수 있다. 트위스트 실린더의 항력 계수는 Re가 3,000에서 10,000까지 증가할 때 약 1%의 항력 증가율을 가지는 반면, 원형 실린더의 경우 항력 증가율이 최대 21%가 되는 것을 확인할 수 있다. 더욱이 트위스트 실린더의 양력 계수는 거의 무시할 수 있을 정 도의 증가율을 가지는 것을 원형 실린더의 양력 계수 증가율과 비교를 통해 확인할 수 있다. 그리고 Re의 함수로 나타낼 수 있 는 원형 실린더의 항력과 양력 계수의 기울기는 트위스트 실린더의 그것보다 약 10배수 크다. 결과적으로, Re 증가에 관계없이 트위스트 실린더가 원형 실린더에 비해 효과적으로 유동을 제어하는 것으로 판단되며 Re 변화에 따른 트위스트 실린더의 항력 및 양력 계수의 특성은 비록 그 증가율이 대폭 감소하였으나, 일반적으로 알려진 아임계 영역에서 나타나는 원형 실린더의 항력 및 양력계수 패턴을 따르는 것을 확인할 수 있다.
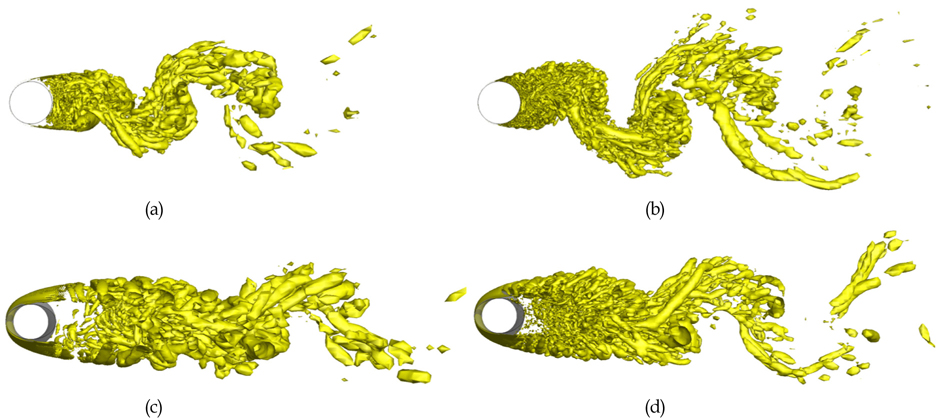
Fig. 5는 Re=3,000과 10,000에서 원형 및 트위스트 실린더 주위의 순간 와 구조들을 각각 나타낸 것이다. 여기서 순간 와 구조는 Zhou et al.(1999)이 제안한 Vortex identification method를 이용하여 나타내었다. 실린더의 형태에 관계없이 Re가 증가함에 따라서 실린더 배면 근방에 다수의 소규모 와동들이 형성되고 실린더 상하부에 나타나는 박리 전단층이 더욱 더 불안정해진 것을 관찰할 수 있다. 이로 인해 원형 및 트위스트 실린더 후방에 상대적으로 좀 더 큰 폭의 카르만 와열 구조가 나타나는 것을 Fig. 5를 통해 확인할 수 있다. 트위스트 실린더의 경우 박리 전단층(Separation shear layer)이 하류쪽으로 길게 늘어지면서 카르만 와열의 발생을 억제 하고 원형 실린더의 후류 형태와 비교하였을 때 후류의 폭이 상대적으로 수축된 것을 Fig. 5(a), (b), (c) 그리고 (d)를 통해 관찰할 수 있다. Re 변화에 따른 순간 와 구조의 특성은 앞서 다룬 항력 및 양력과 밀접한 관계가 있다. 즉, Re가 증가하면 카르만 와열의 폭은 증가하고 실린더 배면 근처에 수많은 소규모 와동들이 형성되어, 이것이 항력과 양력 증가의 요인이 되는 것을 확인할 수 있다. 그러나 원형 실린더의 와동 구조에 비해서 트위스트 실린더의 카르만 와열의 폭은 여전히 작고 소규모 와동들 또한 실런더 배면에 떨어져 형성된 것을 확인할 수 있다.
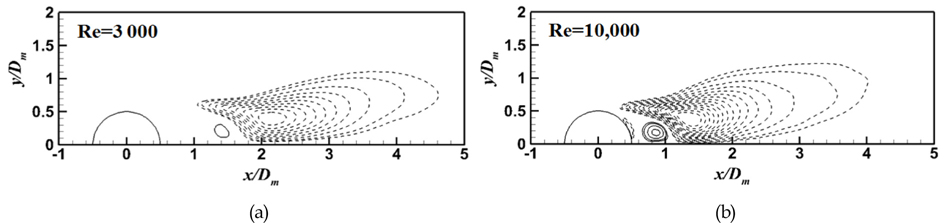
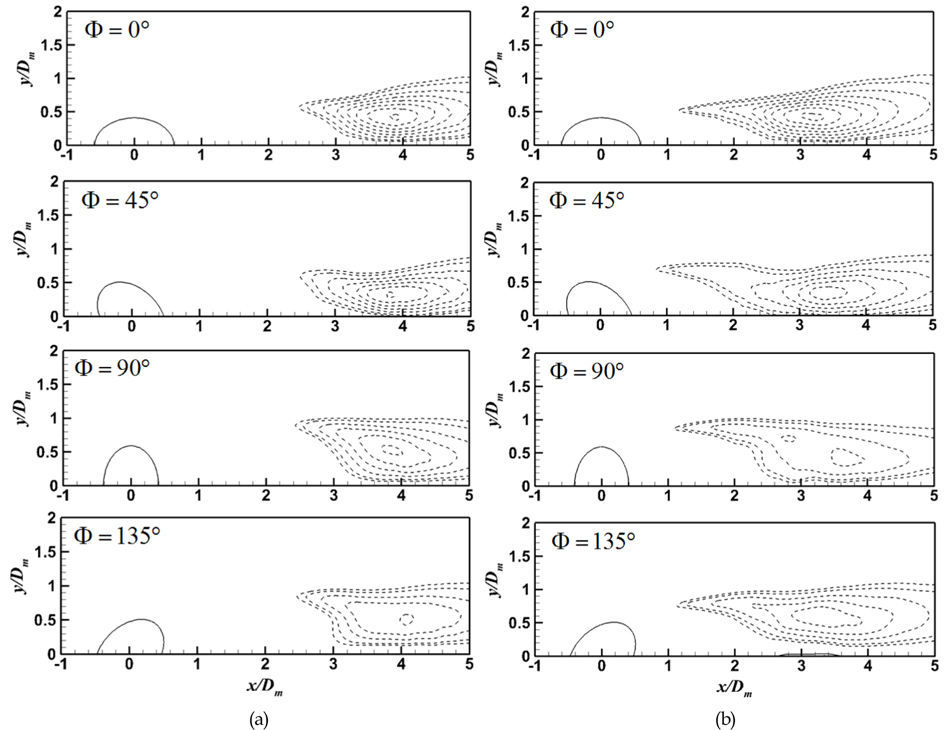
Fig. 6과 7은 Re=3,000과 10,000에서 원형 및 트위스트 실린더 주위 무차원화 된 레이놀즈 응력 분포를 보여준다. 여기서 u′와 v′는 유속방향 및 수직방향의 제곱평균제곱근(Root mean square)속도를 각각 나타낸다. 원형 실린더의 경우, Re가 3,000에서 10,000으로 증가하면 레이놀즈 응력은 실린더 배면에 더 가까이 형성되며, ‘잎엽’(Lobe)과 같은 모양을 가지는 레이놀즈 응력 분포의 ‘꼬리’(Tail) 부분은 상류 쪽으로 더욱 길게 늘어지는 것을 확인할 수 있다. 특히 이 ‘꼬리’가 상류로 길어지는 것은 박리 전단층이 줄어들고 u′와 v′의 상호작용이 실린더에 더욱 더 근접하여 발생하는 것을 의미한다. 즉 Re가 증가하면, 박리 전단층이 실린더 표면에 발생하는 박리점에 더 가까이 형성되어 전단층의 불안정성(Shear layer instability)을 더욱 더 야기 시킨다. 그 결과, 카르만 와열이 실린더 배면 근처에서 큰 폭을 가지며 형성된다. 이러한 특성은 Re 변화에 따른 순간 와 구조의 특성과 일치하는 것을 Fig. 5와 6의 비교를 통해 확인할 수 있으며 앞선 선행 연구들을 통해서도 이미 관찰되어진 바 있다(Unal and Rockwell, 1988; Prasad and Williamson, 1997; Norberg, 1998, Dong et al., 2006).
트위스트 실린더의 경우 Re 증가에 따른 레이놀즈 응력 변화 패턴이 원형 실린더와 유사하나 레이놀즈 응력 분포는 원형 실린더의 그것에 비해 훨씬 더 하류에 위치하고 있고 있으며, 그 최댓값 또한 낮아진 것을 Fig. 6과 7의 비교를 통해 확인할 수 있다. 결과적으로, Re증가에 관계없이 트위스트 실린더가 원형 실린더에 비해 박리 전단층의 불안정성의 발달을 효과적으로 억제하여 박리 전단층이 하류쪽으로 길게 늘어진 작은 폭의 카르만 와열의 발생을 유도하는 것으로 판단된다. 이러한 유동 특성에 기인하여 Re 증가에도 불구하고 트위스트 실린더의 양력 및 항력 계수 증가율은 원형 실린더의 그것들과 비교하여 현저히 낮은 것을 Fig. 4를 통해 확인할 수 있다.
본 연구에서는 뭉툭한 형상을 지닌 해양 칼럼 구조물에서 문제가 되는 와유기 진동의 억제와 저항 저감을 위한 방안으로 나선형 표면 처리된 해양 구조물을 고려하였으며, 대형와모사법을 이용하여 Re 변화에 따른 나선형 해양구조물의 와유기 및 저항 저감 특성에 관한 연구를 수행하였다. 본 연구 결과에 대한 결론은 아래와 같다.
(1) 트위스트 실린더의 항력 계수는 Re가 3,000에서 10,000까지 증가할 때 약 1%의 항력 증가율을 가지는 반면, 원형 실린더의 경우 항력 증가율이 최대 21%가 되는 것을 확인 하였다.
(2) 특히 Re 증가 시, 와유기 진동 관점에서 원형 실린더에 비해 트위스트 실린더의 양력 계수는 거의 무시할 수 있을 정도의 증가율을 가지는 것을 관찰하였다.
(3) 순간 와구조 및 레이놀즈 응력 분포 비교를 통해 트위스트 실린더가 전단층의 불안정성의 발달을 효과적으로 억제하여 Re 증가에도 불구하고 원형 실린더 보다 효과적으로 카르만 와열의 발생을 억제하는 것을 확인하였다.
결과적으로, Re 변화에 관계없이 트위스트 실린더가 원형 실 린더에 비해 효과적으로 유동을 제어하여 와유기 및 저항 저감에 효과적인 것을 확인하였다